江苏省扬州市2019届中考数学一轮复习 微专题路径与最值圆弧型路径

第1课时实数概念及运算姓名班级学习目标：1.理解平方根与立方根的意义，能估算一个数的平方根（立方根）的大致范围。

2.了解无理数和实数的概念，认识实数与数轴上的点一一对应，会求一个数的相反数与绝对值，会比较实数大小，了解近似数与有效数字概念，会按要求取近似值。

3.会进行实数的简单混合运算，并能用运算简化运算。

学习重难点：实数的概念，无理数的定义，科学计数法，实数的混合运算。

学习过程：一、知识梳理（一）实数概念1．整数和统称有理数;叫无理数;有理数和无理数统称．2.数轴的三要素为、和 . 数轴上的点与构成___对应.3.实数a的相反数为________. 若a，b互为相反数，则ba+= .4.非零实数a的倒数为______. 若a，b互为倒数，则ab= .5.绝对值_______ (0)_______ (0)_______ (0)aa aa>⎧⎪==⎨⎪<⎩6.把一个数表示成10na⨯的形式，其中a满足______，n是整数. 7.一般地，一个近似数，四舍五入到哪一位，就说这个近似数精确到_____.（二）实数的有关运算8. 实数加法法则：（1）同号两数相加，取_____符号，并把________相加;（2）异号两数相加，绝对值相等时，和为_____;绝对值不等时，取_____较大的数的符号，并用_______减去_______.9. 实数减法法则：减去一个数，等于加上这个数的_________.10. 实数的乘法法则：两数相乘，同号得_____，异号得_____，并把________相乘.11. 实数的除法法则：两数相除，同号得_____，异号得_____，并把________相除.12.如果一个数的平方等于a，那么这个数叫做a的．a的平方根用符号表示为．其中正的平方根又叫做a 的，记作．13.如果一个数的立方等于a ，那么这个数叫做a 的 ，记作 ．14.求一个数的平方根的运算叫做 ;求一个数的立方根的运算叫做 ． 与乘方互为逆运算．三、精典题例例1 实数120.3π7--、、中，无理数的个数是（ ）A ．2B ．3C ．4D ．5 例2 估计20的算术平方根的大小在（ ）A ．2与3之间B ．3与4之间C ．4与5之间D ．5与6之间例3 如图，A 、B 两点在数轴上表示的数分别是a 、b ，则下列式子中成立的是（ ）A ．0a b +＜B ．a b —＜—C ．1212a b ﹣＞﹣D ．0a b ﹣＞四、课堂练习1．银原子的直径为0.0003微米，把0.0003这个数用科学记数法表示应为（ ）．A ．30.310⨯－B ．4310⨯C ．5310⨯－D ．4310⨯－2．下列运算正确的是（ ）．A 3=±B ．33-=-C ．3=-D ．239-=3．在-5，30sin ︒，30tan ︒，3π，..0.23这六个实数中，无理数的个数为（ ）． A.1 B.2 C.3D.44．若21(2)0x y -++=，则xyz ＝（ ）．A ．－6B ．6C ．0D ．25．计算：301()20162-+= ．6．如果2a ＝，1b ＝－，比较大小：b a a b （填“＜”、“=”或“＞”）．7．定义2a b a b =※－，则()123※※=______．8．若1(1)0n n +-=，则(1)n -＝ ．9．计算：（1）212552⨯+-－． （2）1sin 30π+32-0°+()（3）()2517 2.458612⎛⎫-+-+⨯- ⎪⎝⎭ （4）2324(3)25--÷++-10．观察下面的规律：1=11122⨯－;111=2323⨯－;111=3434⨯－;…… 解答下面的问题：（1）若n 为正整数，请你猜想1(1)n n ⨯+＝ ; （2）求和：1111++++12233420152016⨯⨯⨯⨯＝ . 整式姓名 班级学习目标：1.了解幂的意义，会进行幂的运算，注意“符号”问题和区分各种运算时指数的不同运算。

百度文库，精选试题微专题路径与最值班级：姓名：学习目标：1.掌握动点运动过程中、产生的运动路径类型、及与之相关的最值问题2.通过学习、进一步培养分析问题、解决问题的能力.重难点：用轨迹的观点看问题学习过程：一、圆弧型路径：1.圆定义到定点的距离等于定长的点的轨迹、是以定点为圆心、定长为半径的圆.OA?OBOA、OBPOAAOQP、运动、同分别是射线在：如图、例1向上由上两个动点、点, OBCPQ?4PQQ的中点、在运动向、点运动、且线段是时点由C过程中、点所经过的路径长为定边对直角2.ABPP??APB?BA、90为直径的圆的轨迹是以满足为两个定点、平面内动点、则点B、A（点除外）PABC?AB?6BC4?ABCRtABBC内部的一是△安徽）如图、2016△、中、、、（2例：CP??PBC?PAB长的最小值为个动点、且满足、则线段试题习题，尽在百度．百度文库，精选试题3：定边对定角??PAPB?ABA、BP?为弦所对的的弧、则点满足的轨迹是以为两个定点、平面内动点APBA、B点除外）（AB?2ABACO?AP上一动点、、·省锡中二模）如图、点的半径为2、弦P为优弧3例：（2016 PBCABC的最大面积是（）于点、则△交直线233 D. A. 1 B. 2 C.3二、直线型路径： 1.定距离得平行线：ddlll的距等于定长的距离等于定长的志向的点的轨迹、是平行于直线并且到直线、到定直线.的两条直线MAMMAMPBC8BCABC?当点、连接取：例4如图、在△中、、中点,的是边上一动点、PBC从点的路径长为运动到点、则动点定夹角得直线：2.?ABBAABll上、即：与直线的夹角、若直线不变、则动点始终在定直线已知直线与定点A.点的运动轨迹为直线型DEAEDADABCD为边、动点2：如图、正方形5例的边长为从点运动、以出发、沿边向终点试题习题，尽在百度．百度文库，精选试题DEFGD、E、F、GF经过的路径向排列）（点．求出整个运动过程中、点按顺时针方作正方形长．.3：解析法：建立直角坐标系、用函数知识来解决问题APCAC?8ACABCRt?C?90??6BC以每中、、动点, △开始沿边、从点向点例6：在CBCQ个单位长度的速度运动、1个单位长度的速度运动；同时、动点以每秒从点2开始沿边秒t M0t?PQPQ为、（、当其中一点到达终点时、另一点也随之停止运动、设运动时间为、连接）M. 在整个运动过程中所经过的路径长中点、求点试题习题，尽在百度．百度文库，精选试题三、来回路径型：某些动点问题、确定“直线型”或“圆弧型”路径后、还可能会出现来回运动、需要结合问题的背.景作认真分析、找到关键的临界位置APPCDABCDBCPAPQ 边于、作边上一动点、连接例7：如图、正方形交的边长为4、为BPCQ、当点运动到点从时、.）求点Q所经过的路径长（1. ）求线段AQ的中点所经过的路径长（2三、反思总结本节课你复习了哪些内容？1.通过本节课的学习、你还有哪些困难？2.五、达标检测2ACCF＝RtAC＝6BC＝8ABCF??C＝90、上、中、、点在、1、（2016淮安）如图、并且Δ在边、ABPPEEFCCEFBC距离的最小处、点为边则点上的动点、将Δ到沿直线翻折、点边落在点.值是BDDADAC5BC＝?BAC＝90?3AC＝为直径作圆、连接为、且、上一动点、以、2、如图、ECECE、则的最小值为（交圆于点、连）16．D5C ． A．B．22?13?139试题习题，尽在百度．百度文库，精选试题AB?10C、DABAC?DB?2PCD上的动点、分是线段在线段、点、上、且、如图、已知3APPBABAEPPFBEFEFG、、和等边△设、别以连接、为边在线段的中点为的同侧作等边△PDC 时、从点当点运动到点GPG的最小值为__________ _____________①则点；②线段移动路径的长是AP F BCEMMBCHaABC2、将线的等边三角形是高4、如图、边长为中、所在直线上的一个动点、连接BMBBNHNMHN长度的最小、连接段运动过程中、线段绕点．则在点逆时针旋转60°得到值是__________（0，m）APPAP点逆时针方点坐标为、将线段0点坐标为（8、）、5、在平面直角坐标系中、绕PBOB、ABOB?AB的最小值.、连接、求向旋转90°至ABC?C?90?AC?BC?4cmD ACADE、动点为6、如图、在△、中、=3cm、点边上一点、且AABBDEFBCF．向终点相交于点运动．作∠=45从点°、与边出发沿线段（1）找出图中的一对相似三角形、并说明理由；EAABBF的运动路线长．（2）求动点从点运动的过程中点出发沿线段向终点CD FA E B试题习题，尽在百度．。

2019年中考数学压轴题分析——最短路径问题5：圆形轨迹本篇讲的内容非常非常重要，大家一定要掌握。

不是说对中考重要，而是这个内容在高中也会经常用到。

具体细节大家可以下下面这篇往期文章：圆外一点与圆上一点的距离最值如图，点A为⊙O外一点，点B在圆上，当点B位于何处时AB可以取最大值或最小值？易得，当O，B，A三点共线，且点B位于OA之间时，AB最小；当O，B，A三点共线，且点O位于AB之间时，AB最大．最大值为OA+r，最小值为OA-r【题1】（2019·鄂州）如图，在平面直角坐标系中，已知C（3，4），以点C为圆心的圆与y轴相切．点A、B在x轴上，且OA＝OB．点P 为⊙C上的动点，∠APB＝90°，则AB长度的最大值为．【分析】本题的难点为点P和点A、B都是动点。

不过好在圆C为固定的。

根据直角三角形的性质，我们可以连接OP。

由直角三角形斜边中线的性质，我们可以把AB的值长度转化为2OP的长度。

也就是求点O与圆C上面一点的距离最值。

那大家知道怎么做了吗？有最大值，是不是也有最小值呢？具体看下面的答案吧，顺便也算算最小值是多少。

【答案】16．【解析】解：连接OC并延长，交⊙C上一点P，以O为圆心，以OP为半径作⊙O，交x轴于A、B，此时AB的长度最大，∵C（3，4），∴OC=√(3²+4² )=5，∵以点C为圆心的圆与y轴相切．∴⊙C的半径为3，∴OP＝OA＝OB＝8，∵AB是直径，∴∠APB＝90°，∴AB长度的最大值为16．【题2】（2019·广元）如图，△ABC是⊙O的内接三角形，且AB是⊙O 的直径，点P为⊙O上的动点，且∠BPC＝60°，⊙O的半径为6，则点P到AC距离的最大值是．【分析】点P在圆O上面运动，什么时候到AC的距离取到最值呢？我们可以过点P作AC的垂线段，当垂线过圆心的时候，取到最大值与最小值。

本题仅仅求最大值，那么你可以求出最小值吗？【答案】6+3√3．【解析】解：过O作OM⊥AC于M，延长MO交⊙O于P，则此时，点P到AC的距离最大，且点P到AC距离的最大值＝PM，∵OM⊥AC，∠A＝∠BPC＝60°，⊙O的半径为6，∴OP＝OA＝6，∴OM=√3/2OA=√3/2×6＝3√3，∴PM＝OP+OM＝6+3√3，∴则点P到AC距离的最大值是6+3√3．【总结】上面两题中都有距离的最大值与最小值。

江苏省扬州市2019学中考试卷数学答案解析一、选择题1.【答案】D【解析】中心对称图形绕某一点旋转180°与图形能够完全重合【考点】中心对称图形2.【答案】A【解析】根据二次根式的定义确定四个选项与2-的大小关系，可得比2-小【考点】数的比较大小，无理数3.【答案】D【解析】分式的分母整体提取负号，则每一个都要变号【考点】分式的化简4.【答案】A【解析】众数是出现次数最多的数据【考点】统计，数据的集中趋势与离散程度5.【答案】B【解析】三视图的左视图从物体的左边看【考点】三视图6.【答案】C【解析】坐标系中，一次函数4y x =-+经过第一、二、四象限，所以不经过第三象限【考点】一次函数的图像7．【答案】D【解析】当8n +最大时238283224483n n n n n n n n n n n +++⎧⎧⎪+-+⇒⇒⎨⎨⎩⎪+⎩＞＞＜＜＜＜＞，3n ∴=当3n 最大时28338241038n n n n n n n n n +++⎧⎪--+⇒≤⎨⎪≥+⎩＞＜＜，456789n ∴=，，，，，综上：n 总共有7个【考点】正整数，三角形三边关系8.【答案】C 【解析】反比例函数2y x=-上两个不同的点关于y 轴对称的点 在一次函数y x m =-+图像上∴是反比例函数2y x=与一次函数y x m =-+有两个不同的交点联立两个函数解方程22220y x m x mx x x y x m ⎧=⎪⇒=-+⇒-+=⎨⎪=-+⎩ 有两个不同的交点220x mx +∴-=有两个不等的根280m ∆=-＞根据二次函数图像得出不等式解集220x mx -+=所以mm -＞＜ 【考点】函数图像，方程，数形结合二、填空题9.【答案】617910.⨯【解析】数据1 790.000用科学计数法表示为617910.⨯【考点】科学计数法10.【答案】()()33ab a a +-【解析】先提取公因式，再使用平方差公式因式分解【考点】因式分解11.【答案】0.92【解析】频率接近于一个数，精确到0.01【考点】频率与频数12.【答案】12=1 2.x x =，【解析】()22x x x -=-()22x x x ∴-=-121 2.x x ∴==，【考点】解方程13.2【解析】))20182222⎡⎤=⎣⎦ 【考点】根式的计算，积的乘方14.【答案】128【解析】延长DC 到F矩形纸条折叠ACB BCF ∴∠=∠AB CD ∥26ABC BCF ∴∠=∠=︒52ACF ∴∠=︒180ACF ACD ∠+∠=︒128ACD ∴∠=︒【考点】矩形的性质，折叠问题，等腰三角形，平行线，平角15.【答案】15【解析】AC 是O 的内接正六边形的一边360660AOC ∴∠=︒÷=︒BC 是O 的内接正十边形的一边3601036BOC ∴∠=︒÷=︒603624AOB ∴∠=︒-︒=︒即3602415n n ︒÷=︒∴=【考点】圆心角，圆内正多边形16．【答案】132【解析】连接FC M N ，、分别是DC DF 、的中点2FC MN ∴=75AB BE ==，且ABCD ，EFGB 是正方形∴132MN ∴=【考点】正方形，中位线，勾股定理17.【答案】32π【解析】阴影部分面积=扇形'BB A 的面积+ABCD 的面积-''''A B C D 的面积∴阴影部分面积=扇形'BB A 的面积=2451632360︒=︒ππ【考点】扇形的面积，阴影部分面积18.【答案】40 380【解析】1111,D E AB D F AC ∥∥11111D E CD D F BD AB CB AC BC ∴==，54AB AC ==，1111154D E CD D F BDCB BC ∴==，11111154D E D F CD BD BCCB BC BC ∴+=+==114520D E D F ∴+=有2019组，即20192040380⨯=【考点】相似三角形，比例性质三、解答题19.【答案】（1）1-（2）1a +【解析】（1）142=1-⨯-原式（2）211=1a a a +--=原式【考点】有理数的计算，因式分解，分式化简，三角函数20.【答案】321---，，解：44713393323128242x x x x x x x x x +≤+≥-≥-⎧⎧⎧⇒⇒⇒-≤⎨⎨⎨--⎩⎩⎩＜＜＜＜∴负整数解为321---，， 【考点】一元一次不等式组，取整数，不等式的解集21.【答案】（1）1200.1a b ==，（2）（3）600【解析】（1）360.3120÷=（人）总共120人，120a ∴=121200.1b ÷==（2）如图0.412048⨯=（人）（3）12000.40.1600⨯+=（）（人） 答：该校学生每天阅读时间超过1小时的人数为600人.【考点】数据的收集与整理，统计图的运用22.【答案】（1）14 （2）13【解析】总共有四个，7有一个，所以概率就是114=4÷根据题意得：∴抽到两个素数之和等于30的概率是1412=3÷【考点】概率，素数的定义23.【答案】900米【解析】解设甲工程队每天整治河道m x ，则乙工程队每天整治1500m x -（） 由题意得：360024009001500x x x=⇒=- 经检验的900x =是该方程的解答：甲工程队每天整治河道900米。

江苏省扬州市2019年中考数学试卷一、选择题(本大题共有8题，每题3分，共18分.在每小题所给的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号涂在答题纸相应的．．．．．．表格中．．．) 1、下列图案中，是中心对称图形的是（ ）2、下列各数中，小于-2的是（ ）A. -5B.-3C.-2D.-13、分式x-31可变形为（ ） A.x 31+ B.-x 31+ C.3-x 1 D.-3-x 14、一组数据3，2，4，5，2则这组数据的众数是（ ）A.2B.3C.3.2D.4 5、如图所示物体的左视图是（ ）6、若点P 在一次函数y=-x+4的图像上，则点P 一定不在（ ）A. 第一象限B.第二象限C.第三象限D.第四象限7、已知n 是正整数，若一个三角形的三边长分别是n+2,n+8,3n ，则满足条件的n 的值有（ ）A.4个B.5个C.6个D.7个 8、若反比例函数xy 2-=的图象上有两个不同的点关于y 轴的对称点都在一次函数y=-x+m 的图象上，则m 的取值范围是（ ）A. 22>mB.22-<mB. 22>m 或22-<m D.2222<<-m二、填空题（本大题共有10小题，每小题3分，共30分.不需写出解答过程，请把答案直接填写在答题卡相应位置上）9.2019年5月首届大运河文化旅游博览会在扬州成功举办，京杭大运河全长约1790000米，数据1790000用科学记数法表示为_______ 10. 分解因式：9ab -b a 3=__________11. 扬州某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果如下：从这批玩具中，任意抽取的一个毛绒玩具是优等品的概率的估计值是______(精确到0.01） 12. 一元二次方程2)2(-=-x x x 的根是___________13. 计算：20192018252-5）（）（+的结果是_________ 14.15.如图，AC 是☉O 的内接正六边形的一遍，点B 在弧AC 上，且BC 是☉O 的内接正十边形的一边，若AB 是☉O 的内接正n 边形的一边，则n=16.如图，已知点E 在正方形ABCD 的边AB 上，以BE 为边向正方形ABCD 外部作正方形BEFG ，连接DF ，M 、N 分别是DC 、DF 的中点，连接MN.若AB=7，BE=5,则MN= 17.如图，讲四边形ABCD 绕顶点A 顺时针转45°至AB ’C ’D ’的位置，若AB=16cm ，则图中的阴影部分面积为 cm 2三．解答题（本大题共有10小题，解答时应写出必要得文字说明，证明过程或演算步骤)19. 计算或化简（本题满分8分）（1）0045cos 4--3-8）（π（2）a-111-a a 2+20. （本题满分8分）解不等式组⎪⎩⎪⎨⎧-<-+≤+38413714x x x x ）（，并写出它的所有负整数解。

扬州市2019学初中毕业、升学统一考试数学试题一、选择题（本大题共8小题，每小题3分，共24分）1.下列图案中，是中心对称图形的是( D )A. B. C. D.【考点】：中心对称图形【解析】：中心对称图形绕某一点旋转180°与图形能够完全重合【答案】：D.2.下列个数中，小于-2的数是（A）【考点】：数的比较大小，无理数【解析】：根据二次根式的定义确定四个选项与-2的大小关系，可得【答案】：A.【解析】：分式的分母整体提取负号，则每一个都要变号【答案】：故选B.4.一组数据3、2、4、5、2，则这组数据的众数是( A)A.2B.3C.3.2D.4【考点】：统计，数据的集中趋势与离散程度【解析】：众数是出现次数最多的数据【答案】：故选：A5.如图所示物体的左视图是( B)【考点】：三视图【解析】：三视图的左视图从物体的左边看【答案】：选B.6.若点P 在一次函数4+-=x y 的图像上，则点P 一定不在（ C ）.A.第一象限B. 第二象限C. 第三象限D. 第四象限【考点】：一次函数的图像【解析】：坐标系中，一次函数4+-=x y 经过第一、二、四象限，所以不经过第三象限【答案】：C7.已知n 正整数，若一个三角形的三边长分别是n+2、n+8、3n ，则满足条件的n 的值有( D )A.4个B. 5个C. 6个D. 7个【考点】：正整数，三角形三边关系【解析】：方法一：∵n 是正整数∴n=1时，三边为3,9,3构不成三角形，不符合n=2时，三边为4,10,6构不成三角形，不符合n=3时，三边为5,11,9可以构成三角形，符合n=4时，三边为6,12,12可以构成三角形，符合n=5时，三边为7,13,15可以构成三角形，符合n=6时，三边为8,14,18可以构成三角形，符合n=7时，三边为9,15,21可以构成三角形，符合n=8时，三边为10,16,24可以构成三角形，符合n=9时，三边为11,17,27可以构成三角形，符合n=10时，三边为12,18,30不可以构成三角形，不符合∴总共7个方法二：当n+8最大时424238238832＜＜＜＞＞＜＞n n n n n n n n n n n ⇒⎩⎨⎧⇒⎪⎩⎪⎨⎧++-++++∴n=3当3n 最大时10483283382＜＜＞n n n n n n n n n ≤⇒⎪⎩⎪⎨⎧+≥+--+++∴n=4，5，6，7，8，9综上：n 总共有7个【答案】：选：D.8.若反比例函数xy 2-=的图像上有两个不同的点关于y 轴对称点都在一次函数y =-x +m 的图像上，则m 的取值范围是（ C ）A.22＞mB.22-＜m ①C.22-22＜或＞m mD.2222-＜＜m【考点】：函数图像，方程，数形结合【解析】： ∵反比例函数xy 2-=上两个不同的点关于y 轴对称的点 在一次函数y =-x +m 图像上 ∴是反比例函数x y 2=与一次函数y =-x +m 有两个不同的交点 联立两个函数解方程02222=+-⇒+-=⇒⎪⎩⎪⎨⎧+-==mx x m x x m x y x y ∵有两个不同的交点∴022=+-mx x 有两个不等的根△=m 2-8＞0 根据二次函数图像得出不等式解集 所以22-22＜或＞m m【答案】：C.二、填空题（本大题共10小题，每小题3分，共30分）9.2019年5月首届大运河文化旅游博览会在扬州成功举办，京杭大运河全场约1790000米，数据1790000用科学记数法表示为 1.79×106 .【考点】：科学计数法【答案】：1.79×106【考点】：因式分解，【解析】：先提取公因式，在使用平方差公式因式分解【答案】： ab （3-x ）（3+x ）11.扬州某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果如下从这批玩具中，任意抽取的一个毛绒玩具是优等品的概率的估计值是 0.92 .（精确到0.01）【考点】：频率与频数【解析】：频率接近于一个数，精确到0.01【答案】：0.9212.一元二次方程()22-=-x x x 的根式__x 1=1 x 2=2___.【考点】：解方程【解析】：()22-=-x x x解：()()021=--x x x 1=1 x 2=2【答案】：x 1=1 x 2=2.13.计算：()()20192018252-5+2+ .【考点】：根式的计算，积的乘方【解析】：()()[]()2525252-52018+=++【答案】：25+.14.将一个矩形 纸片折叠成如图所示的图形，若∠ABC=26°，则∠ACD= 128°.【考点】：矩形的性质，折叠问题，等腰三角形，平行线，平角【解析】：解：延长DC 到F∵矩形纸条折叠∴∠ACB=∠∠BCF∵AB∥CD∴∠ABC=∠BCF=26°∴∠ACF=52°∵∠ACF+∠ACD=180°∴∠ACD=128°【答案】：128°15.如图，AC 是⊙O 的内接正六边形的一边，点B 在弧AC 上，且BC 是⊙O 的内接正十边形的一边，若AB 是⊙O 的内接正n 边形的一边，则n=__15_。

第 28 课与圆相关的计算姓名班级学习目标：1.认识正多边形的观点及正多边形与圆的关系，将正多边形问题转变为直角三角形问题．2.会计算圆的弧长、扇形的面积及组合图形的周长与面积．3.理解圆柱、圆锥的侧面睁开图，掌握圆柱、圆锥的侧面积和全面积的计算方法．学习重难点：会计算圆的弧长、扇形的面积及组合图形的周长与面积．学习过程：一、知识梳理⑴各边 ________，各角 _________的多边形叫做正多边形．正多边形的外接圆 ( 或内切圆 ) 的圆心叫做正多边形的 _________．⑵正多边形都是 _ _ 对称图形，一个正n边形共有 ____条对称轴．假如正n边形的边数为偶数，它又是 ____对称图形．⑶圆的相关计算公式 ( 设半径为R，圆心角的度数为n ) ：①圆周长 C ＝_________，弧长 l ＝______________.l②圆面积 S＝______________，S 扇形＝___________＝____________.O r⑷圆锥：②圆锥的侧面睁开图是一个 ________．这个扇形的 ______是圆锥的母线长，这个扇形的 _______是圆锥底面圆的周长．二、典型例题1.与正多边形相关的计算：（1）(2017 ·北京 ) 若正多边形的一个内角是 150°，则该正多边形的边数是( )A. 6B. 12C. 16D. 18（2） (2017 ·沈阳 ) 如图，正六边形ABCDEF内接于⊙O，正六边形的周长是 12，则⊙O的半径是 ___________.2. 与弧长相关的计算：（3）(2017 ·咸宁 ) 如图，⊙O的半径为 3，四边形ABCD内接于⊙O，连接 OB， OD，若B OD＝BCD ，则弧 BD 的长为___________.（4）(2017 ·安顺 ) 如图，一块含有 30°角的直角三角尺ABC，在水平桌面上绕点 C 按顺时针方向旋转到△ A B C 的地点，若 BC＝12 cm ，则极点 A 从开始到结束所经过的路径长为________cm.3．与扇形面积相关的计算：(2017 ·日照 ) 如图，在四边形ABCD中，AB＝CD，AD∥BC，以点B为圆心、 BA 为半径的圆弧与 BC 交于点 E ，四边形 AECD 是平行四边形， AB＝6 ，则扇形 ( 图中涂色部分 ) 的面积是 _________.4.与圆柱 ( 锥) 的侧面睁开图相关的计算：（1）(2017 ·南通 ) 圆锥的底面圆的半径为2，母线长为 6，则侧面积为________.（2）(2017 ·苏州 ) 如图，AB是⊙O的直径，AC是弦，AC＝3，BOC＝2 AOC .若用扇形 OAC (图中涂色部分)围成一个圆锥的侧面，则这个圆锥底面圆的半径是 _____.5. 求暗影部分的面积(2017 ·济宁 ) 如图，在Rt△点 A 逆时针旋转30°后获得ABC 中，ACB＝90 ， AC BC 1.将 Rt △ ABC 绕Rt △ ADE ，则图中暗影部分的面积是________.三、中考展望：1.如图，在△ ABC 中， C＝90 ， BAC 的均分线交 BC 于点 D ，点 O 在 AB 上，以点 O 为圆心、 OA 为半径的圆恰巧经过点 D ，分别交 AC， AB 于点 E，F .(1)试判断直线 BC 与⊙ O 的地点关系，并说明原因;(2)若 BD＝2 ， BF＝2 ，求暗影部分的面积．(结果保存)四、反省总结1、本课复习了哪些内容？2、你还有什么疑惑？五、达标检测1.(2017 ·苏州 ) 如图，在正五边形ABCDE中，连结BE，则ABE的度数为( )A. 30 °B. 36°C. 54°D. 72 °第 1 题第 4 题第 5 题2. (2017 ·滨州) 若正方形的外接圆半径为2，则其内切圆的半径为_______.3.(2017 ·天门 ) 一个扇形的弧长是10 cm，面积是60 cm2，则此扇形的圆心角的度数是 ( )A. 300 °B. 150 °C. 120°D. 75 °4.(2017 ·南宁 ) 如图，⊙O是△ABC的外接圆，BC＝2，BAC＝30，则劣弧BC 的长为_____5. (2017 ·莱芜 ) 如图，在Rt△ABC中，BCA＝90 ，BAC＝30 ， BC＝2 ，将Rt △ ABC 绕 A 点顺时针旋转90°获得Rt△ADE，则BC扫过的面积 ( 涂色部分)为______6.(2017 ·遵义 ) 一个正多边形的一个外角为 30°，则它的内角和为__________.7. (2017·聊城 ) 已知圆锥形工件的底面直径是40 cm ，母线长30 cm ，其侧面睁开图圆心角的度数为________.8.(2017 ·淮安 ) 如图，在△ABC中，ACB＝90，O是边AC上一点，以O为圆心、 OA 长为半径的圆分别交 AB，AC 于点 E， D ，在 BC 的延伸线上取点 F ，使得 BF＝EF，EF 与 AC 交于点 G .(1)试判断直线 EF 与⊙ O 的地点关系，并说明原因;(2)若 OA＝2， A＝30 ，求图中暗影部分的面积．。

整式姓名 班级学习目标：1.了解幂的意义、会进行幂的运算、注意“符号”问题和区分各种运算时指数的不同运算.2.会进行整式的乘法运算、其中单项式乘法是关键、其他乘除都要转化为单项式乘法.3.运用乘法公式进行计算、要注意观察每个因式的结构特点、灵活运用公式使计算简化.4.理解因式分解的意义、会解答简单的因式分解问题.学习重难点：理解因式分解的意义、会解答简单的因式分解问题学习方法：学习过程：【复习指导】1．分解因式的概念（1）分解因式：把一个多项式化成几个____________的形式.（2）分解因式与整式乘法的关系：2．分解因式的基本方法：（1）提公因式法：_____________=++mc mb ma .（2）运用公式法：（1）平方差公式：_________22=-b a ；（2）完全平方公式：__________222=+±b ab a .知识点1：因式分解例1：下列四个多项式中、能因式分解的是（ ）A ．21a +B ．269a a +﹣C ．25x y +D ．25x y ﹣ 例2：因式分解：28116a a +-=（） 知识点2：求代数式的值例1：若23a b ==，，则224a ab -的值为 例2：已知32ab a b =-+=，，求代数式33a b ab +的值例3：如图、在边长为a 的正方形中、剪去一个边长为b 的小正方形a b >（）,将剩余部分拼成一个梯形、根据两个图形阴影部分面积的关系、可以得到一个关于a 、b 的恒等式为（ ）A ．2222a b a ab b --=+（） B ．2222a b a ab b -=++（） C ．22)(a b a b a b -=-+（）D ．2a ab a a b +=+（）知识点4：开放性问题例：给出三个整式22222x xy y xy x ++，，中、请你任意选出两个进行加（减）法运算、使所得整式可以因式分解、并进行因式分解.基础巩固1.因式分解：34a a -=2.把多项式22369xy x y y --分解因式、最后结果为3.把下列各式分解因式：（1）222 416a a +-（） （2）()()22827x y x x y xy --++4.甲、乙两名同学在将2x ax b ++分解因式时、甲看错了b 、分解结果为()()24x x ++；乙看错了a 、分解结果为()()19x x ++.请你分析一下、a b 、的值分别为多少？并写出正确的因式分解过程.【变式拓展】1.若多项式24x mx ++能用完全平方公式因式分解、则m 的值为 2. 先阅读后作答：我们已经知道、根据几何图形的面积关系可以说明完全平方公式、实际上还有一些等式也可以用这种方式加以说明、例如：()()22223 a b a b a ab b ++=++、就可以用图1的面积关系来说明．（1） 根据图2写出一个等式 ： （2）已知等式()()()2 x p x q x p q x pq ++=+++、请你画出一个相应的几何图形加以说明.例3（中考指要）阅读理解：用“十字相乘法”分解因式223x x --的方法.（1）二次项系数212=⨯； （2）常数项 3131(3)-=-⨯=⨯-验算：“交叉相乘之和”；132(1)1⨯+⨯-= 1(1)235⨯-+⨯= 1(3)211⨯-+⨯=- 112(3)5⨯+⨯-=-（3）发现第③个“交叉相乘之和”的结果1(3)211⨯-+⨯=-、等于一次项系数-1、即22(1)(23)232323x x x x x x x +-=-+-=--、则223(1)(23)x x x x --=+-.像这样、通过十字交叉线帮助、把二次三项式分解因式的方法、叫做十字相乘法.仿照以上方法、分解因式：23512x x +-= ．【反馈练习】1.下面的多项式在实数范围内能因式分解的是 （ ）2.A x y + 2.B x y - 2.1C x x ++ 2.21D x x -+2.把2244ax axy ay -+分解因式的结果是 （ ）244A a x xy y -+．（） .4B a x y -2（） 2.2C a x y -（） ()2.2D a x y - 3.若24436x mx ++是完全平方式、结果正确的是 （ ）A.2B.±2C.-6D. ±6 5．如图、在边长为2a 的正方形中央剪去一边长为2a +（）的小正方形2a （＞）、将剩余部分剪开密铺成一个平行四边形、则该平行四边形的面积为（ ）2.4A a + 2.24B a a + 2 .344C a a ﹣﹣ 242D a a ．﹣﹣6.把39x x -因式分解、结果为7.已知43a b a b +=-=，、则22a b -=8.在实数范围内分解因式：36x x -=9.因式分解：2221a a +-=（）10.已知2=+b a 、1=ab 、则22ab b a +的值为________.11.若12+=n m 、则________4422=+-n mn m .12.如果有理数a b ，同时满足()()22322355a b a b +++-=、那么a b +=13.多项式25x mx ++因式分解得()()5x x n ++、则m = 、n =14.因式分解：（1）3269x x x -+； （2）()()131x x --+15.如果一个正整数能表示为两个连续偶数的平方差、那么称这个正整数为“神秘数”.例如： 2420=- 、221242=- 、222064=-因此、4,12,20都是神秘数.（1）28和2012这两个数是神秘数吗？为什么？（2）设两个连续偶数为222k k +和（其中k 取非负数）、由这两个连续偶数构造的神秘数是4的倍数吗？为什么？（3）两个连续奇数的平方数（取正数）是神秘数吗？为什么？。

微专题 路径与最值（圆弧型路径） 班级： 姓名： 学习目标：1.掌握动点运动过程中，产生的运动路径类型，及与之相关的最值问题 2.通过学习，进一步培养分析问题，解决问题的能力。

重难点：用轨迹的观点看问题学习过程一．知识储备1.圆定义：圆是到 的距离等于 的点的集合。

2.直径所对的圆周角是 。

3.同弧所对的圆周角 。

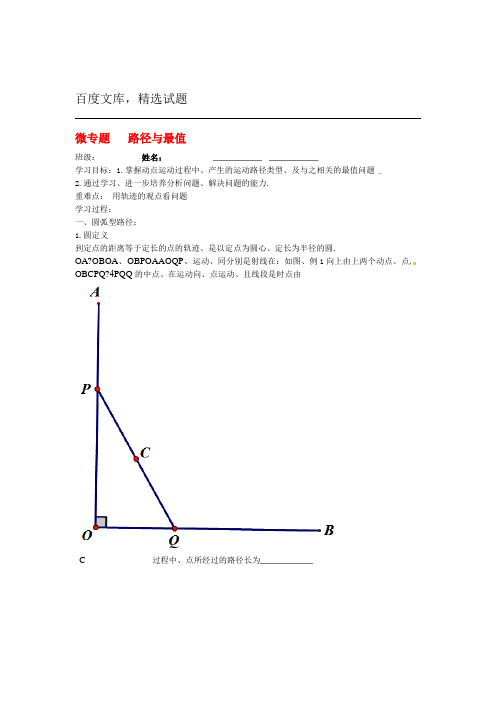
二、典型例题例1：如图，OA OB ⊥,P Q 、分别是射线OA OB 、上两个动点，点P 在OA 上由A 向O 运动，同时点Q 由O 向B 运动，且4PQ =，点C 是线段PQ 的中点，在运动过程中，点C 所经过的路径长为例2：（2016安徽）如图，Rt △ABC 中，AB BC ⊥，6AB =，4BC =，P 是△ABC 内部的一个动点，且满足PAB PBC ∠=∠，则线段CP 长的最小值为例3：（2016·省锡中二模）如图，O 的半径为2，弦2AB =，点P 为优弧AB 上一动点，AC AP ⊥交直线PB 于点C ，则△ABC 的最大面积是（ ）A. 1B. 2C. 233D. 3三、中考预测 （2014•成都）如图，在边长为2的菱形ABCD 中，∠A=60°，M 是AD 边的中点，N 是AB 边上的一动点，将△AMN 沿MN 所在直线翻折得到△A′MN，连接A′C，则A′C 长度的最小值是 ．四、反思总结1.本节课你复习了哪些内容？2.通过本节课的学习，你还有哪些困难？五、达标检测（2016淮安）如图，在Rt ΔABC 中，90C ∠︒＝，6AC ＝，8BC ＝，点F 在边AC 上，并且2CF ＝，点E 为边BC 上的动点，将ΔCEF 沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是 .、如图，3AC ＝，5BC ＝，且90BAC ∠︒＝，D 为AC 上一动点，以AD 为直径作圆，连接BD 交圆于E 点，连CE ，则CE 的最小值为（ ）A ．213-B ．213+C ．5D ．916PBC FE A。

课题：第9课时 平面直角坐标系班级： 姓名：学习目标：1.理解直角坐标系的有关概念、会根据坐标确定点的位置和由点的位置确定坐标、并能够在方格纸上建立适当的直角坐标系描述物体的位置；2.能够在同一直角坐标系内感受图形变换前后点的坐标的变化规律、灵活运用不同的方式确定物体的位置.学习重、难点：直角坐标系中的点与坐标的对应关系.学习过程：一．知识梳理1．有序实数对 平面内的点和有序实数对是 的关系、即平面内的任何一个点可以用一对 来表示；反过来每一对有序实数都表示平面内的一个点．2．平面内点的坐标规律(1)各象限内点的坐标的特征点P(x 、y)在第一象限 则 ； 点P (x 、y)在第二象限 则点P(x 、y)在第三象限 则 ； 点P(x 、y)在第四象限 则(2)坐标轴上的点的坐标的特征点P(x 、y)在x 轴上,则 、x 为任意实数；点P(x 、y)在y 轴上,则 、y 为任意实数；点P(x 、y)在坐标原点,则3．平行于坐标轴的直线上的点的坐标特征(1)平行于x 轴(或垂直于y 轴)的直线上点的 相同、横坐标为不相等的实数．(2)平行于y 轴(或垂直于x 轴)的直线上点的 相同、纵坐标为不相等的实数．2．各象限角平分线上的点的坐标特征(1) 若点P(x 、y)为一、三象限角平分线上的点、则 .(2) 若点P(x 、y 为第二、四象限角平分线上的点、则 .3．对称点的坐标特征(1)点P(x 、y)关于x 轴的对称点P 1的坐标为 .(2)关于y 轴的对称点P 2的坐标为 .(3)关于原点的对称点P 3的坐标为 .4.坐标与距离（1））点P(x 、y)到x 轴的距离为 .到y 轴的距离为 . 到原点的距离为 .（2）若1122(,),(,)A x y B x y 、则线段AB 的中点P 的坐标为 、线段AB 的长度为二、典型例题1.对称点的特征已知点P(3、－4)、填写下列空格：点P 关于x 轴对称的点的坐标为 ；点P 关于y 轴对称的点的坐标为 ；点P 关于原点对称的点的坐标为 ；关于点)0,3(对称的点的坐标为 ；2.坐标与距离点P 到x 轴的距离为 ；点P 到y 轴的距离为 ；点P 到原点的距离为 ；点P 到)1,2(1--P 的距离为 ；3.象限内点的坐标特征（1）若点M （x 、y ）满足2()x y -＝222x y +-、则点M 所在象限是第 象限.（2）若a 为任意实数、点(.2),P a a +一定不再第（ ）象限A.一B. 二C. 三D.四4.图形变换与坐标（1）如图、把“QQ ”笑脸放在直角坐标系中、已知左眼A 的坐标是（－2、3）、嘴唇C 点的坐标为（－1、1）、则将此“QQ ”笑脸向右平移3个单位后、右眼B 的坐标是 .（2）如图、正方形OABC 的两边OA 、OC 分别在x 轴、y 轴上、点D （5、3）在边AB 上、以C 为中心、把△CDB 旋转90°、则旋转后点D 的对应点D′的坐标是（3）(2014黔西南州)在平面直角坐标系中、对于平面内任一点（m 、n ）、规定以下两种变换：（1）f （m 、n ）=（m 、﹣n ）、如f （2、1）=（2、﹣1）；（2）g （m 、n ）=（﹣m 、﹣n ）、如g （2、1）=（﹣2、﹣1）按照以上变换有：f[g （3、4）]=f （﹣3、﹣4）=（﹣3、4）、那么g[f （﹣3、2）]= ．（4）（2017温州）如图、我们把1、1、2、3、5、8、13、21、…这组数称为斐波那契数列、为了进一步研究、依次以这列数为半径作90°圆弧、、、…得到斐波那契螺旋线、然后顺次连结P 1P 2、P 2P 3、P 3P 4、…得到螺旋折线（如图）、已知点P 1（0、1）、P 2（﹣1、0）、P 3（0、﹣1）、则该折线上的点P 9的坐标为（ ）A ．（﹣6、24）B ．（﹣6、25）C ．（﹣5、24）D ．（﹣5、25）5.坐标与图形在棋盘中建立如图所示的直角坐标系、三颗棋子A 、O 、B 的位置如图、它们的坐标分别是()1,1- 、（0、0）、（1、0）.（1）如图2、添加棋C 子、使四颗棋子A 、O 、B 、C 成为一个轴对称图形、请在图中画出该图形的对称轴；（2）在其他格点位置添加一颗棋子P 、使四颗棋子A 、O 、B 、P 成为轴对称图形、请直接写出棋子P 的位置的坐标. （写出2个即可）三、反思总结1.本节课你复习了哪些内容？2.通过本节课的学习、你还有哪些困难？四、达标检测1.若点A （a+1、b ﹣2）在第二象限、则点B （﹣a 、b+1）在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2. 将点P （-2、3）向右平移3个单位得到点P 1、点P 2与点P 1关于原点对称、则点P 2的坐标是 .3.（2017.百色）如图、在正方形OABC中、O为坐标原点、点C在y轴正半轴上、点A的坐标为（2、0）、将正方形OABC沿着OB方向平移12OB个单位、则点C的对应点坐标为．4.（2014•吉林）如图、直线y=2x+4与x、y轴分别交于A、B两点、以OB为边在y轴右侧作等边三角形OBC、将点C向左平移、使其对应点C′恰好落在直线AB上、则点C′的坐标为．5.（2017无锡）操作：“如图1、P是平面直角坐标系中一点（x轴上的点除外）、过点P作C xP⊥轴于点C、点C绕点P逆时针旋转60得到点Q．”我们将此由点P得到点Q的操作称为点的T变换．（1）点(),a bP经过T变换后得到的点Q的坐标为；若点M经过T变换后得到点(6,N、则点M的坐标为．6.如图、已知点A(－4、2)、B(－1、－2)、平行四边形ABCD的对角线交于坐标原点O．(1) 请直接写出点C、D的坐标；(2) 写出从线段AB到线段CD的变换过程；(3) 直接写出平行四边形ABCD的面积.7.（2017达州）探究：小明在求同一坐标轴上两点间的距离时发现、对于平面直角坐标系内任意两点P1（x1、y1）、P2（x2、y2）、可通过构造直角三角形利用图1得到结论：P1P2他还利用图2证明了线段P1P2的中点P（x、y）P的坐标公式：①已知点M（2、﹣1）、N（﹣3、5）、则线段MN长度为；②直接写出以点A（2、2）、B（﹣2、0）、C（3、﹣1）、D为顶点的平行四边形顶点D的坐标：；（选做）如图、点P（2、n）在函数43y x（x≥0）的图象OL与x轴正半轴夹角的平分线上、请在OL、x轴上分别找出点E、F、使△PEF的周长最小、简要叙述作图方法、并求出周长的最小值．。