EVIEWS用面板数据模型预测
- 格式:doc
- 大小:1.90 MB
- 文档页数:50

面板数据模型的分析及Eviews实现一、面板数据和模型概述在经济学研究和实际应用中,我们经常需要同时分析和比较横截面观察值和时间序列观察值结合起来的数据,即:数据集中的变量同时含有横截面和时间序列的信息。
这种数据被称为面板数据(panel data),它与我们以前分析过的纯粹的横截面数据和时间序列数据有着不同的特点。
简单地讲,面板数据因同时含有时间序列数据和截面数据,所以其统计质既带有时间序列的性质,又包含一定的横截面特点。
因而,以往采用的计量模型和估计方法就需要有所调整。
例1 表1中展示的数据就是一个面板数据的例子。
其他类似的例子还有:历次人口普查中有关不同年龄段的受教育状况;同行业不同公司在不同时间节点上的产值等。
这里,不同的年龄段和公司代表不同的截面,而不同时间节点数据反映了数据的时间序列性。
研究和分析面板数据的模型被称为面板数据模型(panel data model)。
它的变量取值都带有时间序列和横截面的两重性。
一般的线性模型只单独处理横截面数据或时间序列数据,而不能同时分析和对比它们。
面板数据模型,相对于一般的线性回归模型,其长处在于它既考虑到了横截面数据存在的共性,又能分析模型中横截面因素的个体特殊效应。
当然,我们也可以将横截面数据简单地堆积起来用回归模型来处理,但这样做就丧失了分析个体特殊效应的机会。
二、一般面板数据模型介绍 符号介绍:ity ——因变量在横截面i 和时间t 上的数值;j it x ——第j 个解释变量在横截面i 和时间t 上的数值;假设:有K 个解释变量,即K j ,,2,1 =;有N 个横截面,即N i ,,2,1 =; 时间指标T t ,,2,1 =。
记第i 个横截面的数据为⎪⎪⎪⎪⎪⎭⎫⎝⎛=iT i i i y y y y21; ⎪⎪⎪⎪⎪⎭⎫⎝⎛=K iT iT iT Ki i i K i i i i x x x x x x x x x X 212221212111;⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=iT i i i μμμμ 21 其中对应的i μ是横截面i 和时间t 时随机误差项。


eviews实验指导ARIMA模型建模与预测在数据分析和时间序列预测的领域中,ARIMA 模型是一种非常强大且实用的工具。
通过eviews 软件来实现ARIMA 模型的建模与预测,可以帮助我们更高效地处理和分析数据,做出更准确的预测。
接下来,让我们逐步深入了解如何使用eviews 进行ARIMA 模型的建模与预测。
首先,我们要明白什么是 ARIMA 模型。
ARIMA 全称为自回归移动平均整合模型(Autoregressive Integrated Moving Average Model),它由三个部分组成:自回归(AR)部分、差分(I)部分和移动平均(MA)部分。
自回归(AR)部分是指当前值与过去若干个值之间存在线性关系。
例如,如果说一个时间序列在 AR(2)模型下,那么当前值就与前两个值有关。
移动平均(MA)部分则表示当前值受到过去若干个随机误差项的线性影响。
差分(I)部分用于将非平稳的时间序列转化为平稳序列。
平稳序列在统计特性上,如均值、方差等,不随时间变化而变化。
在 eviews 中进行 ARIMA 模型建模与预测,第一步是数据的导入和预处理。
打开 eviews 软件后,选择“File”菜单中的“Open”选项,找到我们要分析的数据文件。
数据的格式通常可以是 Excel、CSV 等常见格式。
导入数据后,需要对数据进行初步的观察和分析,了解其基本特征,比如均值、方差、趋势等。
接下来,判断数据的平稳性。
这是非常关键的一步,因为 ARIMA 模型要求数据是平稳的。
我们可以通过绘制时间序列图、计算自相关函数(ACF)和偏自相关函数(PACF)来直观地判断数据的平稳性。
如果时间序列图呈现明显的趋势或周期性,或者自相关函数和偏自相关函数衰减缓慢,那么很可能数据是非平稳的。
对于非平稳的数据,我们需要进行差分处理。
在 eviews 中,可以通过“Quick”菜单中的“Generate Series”选项来实现差分操作。

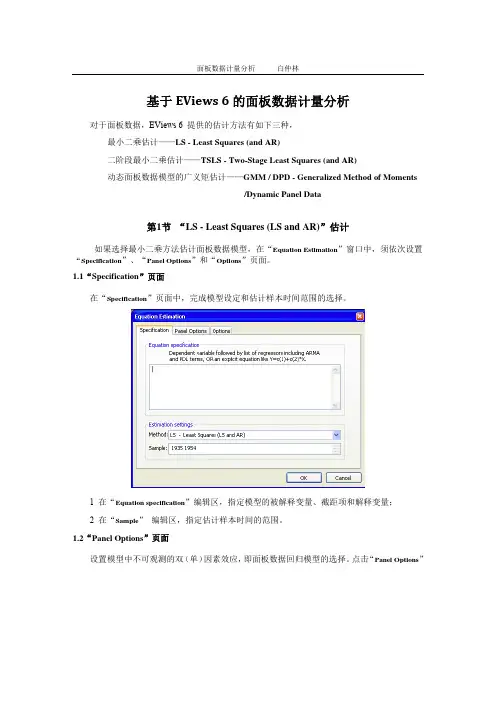
基于EViews 6的面板数据计量分析对于面板数据,EViews 6 提供的估计方法有如下三种,最小二乘估计——LS - Least Squares (and AR)二阶段最小二乘估计——TSLS - Two-Stage Least Squares (and AR)动态面板数据模型的广义矩估计——GMM / DPD - Generalized Method of Moments/Dynamic Panel Data第1节“LS - Least Squares (LS and AR)”估计如果选择最小二乘方法估计面板数据模型,在“Equation Estimation”窗口中,须依次设置“Specification”、“Panel Options”和“Options”页面。
1.1“Specification”页面在“Specification”页面中,完成模型设定和估计样本时间范围的选择。
1 在“Equation specification”编辑区,指定模型的被解释变量、截距项和解释变量;2 在“Sample”编辑区,指定估计样本时间的范围。
1.2“Panel Options”页面设置模型中不可观测的双(单)因素效应,即面板数据回归模型的选择。
点击“Panel Options”该页面包含三方面内容。
1 效应设置在“Effects specification”选择区,设定面板数据模型的个体效应和时间效应,可选择的选项有“None”、“Fixed”和“Random”,分别表示“无效应”、“固定效应”和“随机效应”。
如果选择了“Fixed”或“Random”,EViews在输出结果中自动添加一个共同常数,即截距项,以保证效应之和为零。
否则,截距项必要时,须在“Specification”页面的“Equation specification”编辑区设定模型截距项。
2 GLS加权设置“GLS Weights”可以在下拉框中选择如下选项之一。
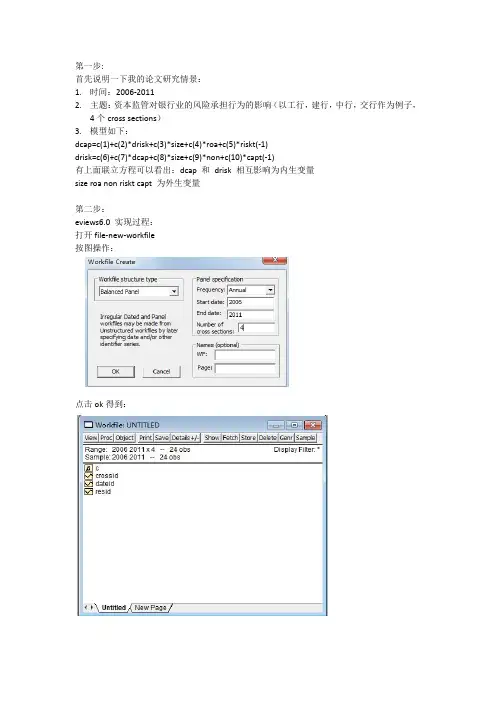
第一步:首先说明一下我的论文研究情景:1.时间:2006-20112.主题:资本监管对银行业的风险承担行为的影响(以工行,建行,中行,交行作为例子,4个cross sections)3.模型如下:dcap=c(1)+c(2)*drisk+c(3)*size+c(4)*roa+c(5)*riskt(-1)drisk=c(6)+c(7)*dcap+c(8)*size+c(9)*non+c(10)*capt(-1)有上面联立方程可以看出:dcap 和drisk 相互影响为内生变量size roa non riskt capt 为外生变量第二步:eviews6.0 实现过程:打开file-new-workfile按图操作:点击ok得到:点击object-new objectType选pool,ok:跳出的横框:Cross Section Identifiers 填入数据变量名称:(这是纵轴的)GSYHJSYHZGYHJTYH(前面提及的四大银行)然后点view-spreadsheet(stacked data)series list小框输入(这是横轴的变量名称)dcap drisk size roa non riskt capt点击edit+/- 手动输入数据或用import导入数据或粘贴复制进去也行:此时点object-new object,这次type选择system 用以联立方程分析:在system框内输入联立方程和工具变量:dcap=c(1)+c(2)*drisk+c(3)*size+c(4)*roa+c(5)*riskt(-1)drisk=c(6)+c(7)*dcap+c(8)*size+c(9)*non+c(10)*capt(-1)inst dcap drisk size roa non riskt(-1) capt(-1)点右上方的estimate,method选择TSLS(两阶段最小二乘估计):整个过程就是先建立workfile再建立panel data最后建立联立方程systemTSLS估计即可。


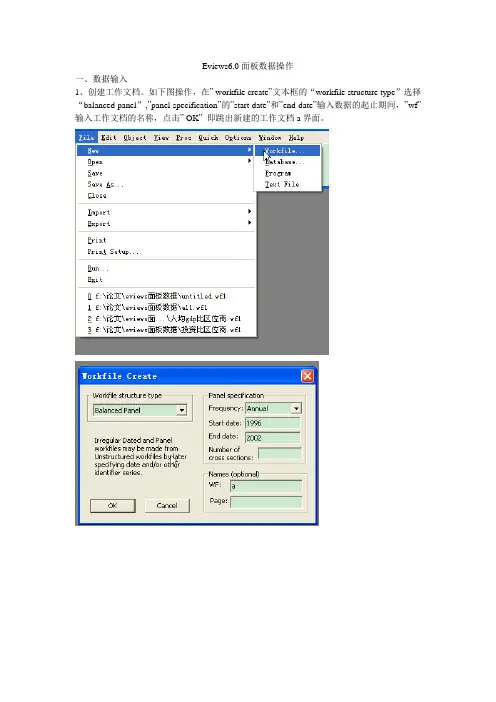
Eviews6.0面板数据操作一、数据输入1、创建工作文档。
如下图操作,在” workfile create”文本框的“workfile structure type”选择“balanced panel”,”panel specification”的”start date”和”end date”输入数据的起止期间,”wf”输入工作文档的名称,点击” OK”即跳出新建的工作文档a界面。
2、创建新对象。
操作如下图。
在”new object”文本框的”type of object”选择”pool”,”name for object ”输入新对象的名称。
创建成功后的界面如下面第3张图所示。
3、输入数据。
双击”workfile”界面的,跳出”pool”界面,输入个体。
一般输入方式为如下:若上海输入_sh,北京输入_bj,…。
个体输入完成后,点击该界面的键,在跳出的”series list”输入变量名称,注意变量后要加问号。
格式如下:y? x?。
点击”OK”后,跳出数据输入界面,如下面第4张图所示。
在这个界面上点击键,即可以输入或者从EXCEL处复制数据。
在输入数据后,记得保存数据。
保存操作如下:在跳出的“workfile save”文本框选择“ok”即可,则自动保存到我的文档。
然后在“workfile”界面如下会显示保存路径:d:\my documents\a.wf1。
若要保存到自己选择的路径下面,则在保存时选择“save as”,在跳出的文本框里选择自己要保存的路径以及命名文件名称。
4、单位根检验。
一般回归前要检验面板数据是否存在单位根,以检验数据的平稳性,避免伪回归,或虚假回归,确保估计的有效性。
单位根检验时要分变量检验。
(补充:网上对面板数据的单位根检验和协整检验存在不同意见,一般认为时间区间较小的面板数据无需进行这两个检验。
)(1)生成数据组。
如下图操作。
点击”make group”后在跳出的”series list”里输入要单位根检验的变量,完成后就会跳出如下图3所示的组数据。

这里N 指截面个体的个数,T 时期个数,k 是解释变量个数。
如果计算的F 统计量的值大于设定的显著性水平的临界值(如5%或10%),拒绝原假设,选择个体固定效应模型更合适;如果小于临界值,接受原假设,混合数据模型更适合。
在stata 中计算临界值disp invFtail(n1,n2,p) 或卡方disp invchi2tail(n,p) 再构造两个F 统计量以检验方程是否符合混合模型、变截矩模型或变系数模型。
3121()/(1)(1)[(1)(1),(*(1)]/(*(1)
S S N k F F N k N T k S N T k −−+=−+−−−−∼如果上述值大于给定的临界值,则拒绝原假设混合数据模型,对不变系数的模型作进一步的检验
2111()/(1)[(1),(*(1)]/(*(1)
S S N k F F N k N T k S N T k −−=
−−−−−∼如果上述值大于给定的临界值,则拒绝原假设,用变系数模型合适,否则,用变截距模型较合适。
S1指变系数模型残差平方和,S2指固定效应模型残差平方和,S3指混合数据模型残差平方和。
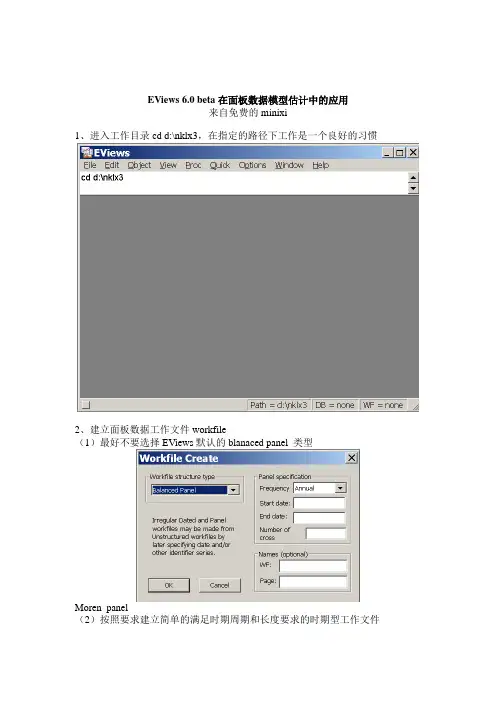
EViews 6.0 beta在面板数据模型估计中的应用来自免费的minixi1、进入工作目录cd d:\nklx3,在指定的路径下工作是一个良好的习惯2、建立面板数据工作文件workfile(1)最好不要选择EViews默认的blanaced panel 类型Moren_panel(2)按照要求建立简单的满足时期周期和长度要求的时期型工作文件3、建立pool对象(1)新建对象(2)选择新建对象类型并命名(3)为新建pool对象设置截面单元的表示名称,在此提示下(Cross Section Identifiers: (Enter identifiers below this line )输入截面单元名称。
,建议采用汉语拼音,例如29个省市区的汉语拼音,建议在拼音名前加一个下划线“_”,如图关闭建立的pool对象,它就出现在当前工作文件中。
4、在pool对象中建立面板数据序列双击pool对象,打开pool对象窗口,在菜单view的下拉项中选择spreedsheet (展开表)在打开的序列列表窗口中输入你要建立的序列名称,如果是面板数据序列必须在序列名后添加“?”。
例如,输入GDP?,在GDP后的?的作用是各个截面单元的占位符,生成了29个省市区的GDP的序列名,即GDP后接截面单元名,再在接时期,就表示出面板数据的3维数据结构(1变量2截面单元3时期)了。
请看工作文件窗口中的序列名。
展开表(类似excel)中等待你输入、贴入数据。
(1)打开编辑(edit)窗口(2)贴入数据(3)关闭pool窗口,赶快存盘见好就收6、在pool窗口对各个序列进行单位根检验选择单位根检验设置单位根检验单位根检验结果注意检验方法和两种检验的零假设:Null: Unit root (assumes common unit root process)各截面有相同的单位根Null: Unit root (assumes individual unit root process)允许各截面有不同单位根其中,Levin, Lin & Chu t*检验拒绝含有单位根的零假设,即拒绝非平稳7、在pool窗口对面板数据组合进行协整检验选择进行协整检验协整检验设置对话框,注意有3种检验方法(test type)协整检验结果,同样要注意两种假定(含有AR,即含有单位根,非协整),两种零假设都是非协整,小概率事件发生拒绝非协整。
eviews实验心得与体会在进行Eviews实验时,我深刻体会到了其强大的数据分析和预测能力。
本文将分享我在实验过程中的心得与体会。
首先,Eviews是一款专业的统计软件,它在数据处理和模型建立方面具有独特的优势。
我喜欢它简洁而直观的用户界面,使得学习和使用变得更加容易。
在我的实验中,我首先将所需的数据导入Eviews,并进行了数据的初步清理和整理。
Eviews提供了丰富的数据处理函数和命令,使得数据清洗和变量转换变得高效且精确。
其次,Eviews强大的模型建立和分析能力为我的实验提供了坚实的基础。
在实验过程中,我先后应用了回归模型、时间序列模型和面板数据模型进行分析。
通过Eviews提供的模型建立向导和方便的命令操作,我能够轻松地构建出符合要求的模型,并对模型进行参数估计和显著性检验。
Eviews还提供了丰富的模型诊断工具,使我能够全面评估模型的拟合效果和稳健性。
在实验中,我还深刻领悟到了数据的选择和处理对实验结果的重要性。
Eviews提供了多种数据选择和处理的方法,如样本选择、变量选择和数据平滑等。
合理选择和处理数据可以使实验结果更加准确和可靠。
除了数据的选择和处理外,Eviews还提供了强大的数据可视化功能。
我发现通过绘制图表和图像,可以更直观地展示数据的特征和趋势,对于研究和理解问题起到了重要作用。
Eviews的图表功能丰富多样,操作简便,能够满足不同实验需求的可视化要求。
总结而言,Eviews作为一款专业的统计软件,在实验中给我带来了很多的便利和启示。
它的简洁直观的用户界面、强大的数据处理和模型建立能力,使得我能够高效地进行实验设计和数据分析。
同时,Eviews丰富的数据可视化工具也让我更加直观地理解和呈现实验结果。
通过这次实验,我不仅学到了更多的统计知识和实战技巧,更重要的是培养了我的数据分析能力。
Eviews作为一款功能强大的统计软件,不仅为实验提供了便捷和准确的工具,更激发了我对数据分析的兴趣和热情。
第8讲用面板数据模型预测1.面板数据定义时间序列数据或截面数据都是一维数据。
时间序列数据是变量按时间得到的数据;截面数据是变量在固定时点的一组数据。
面板数据是同时在时间和截面上取得的二维数据。
面板数据也可以定义为相同截面上的个体在不同时点的重复观测数据或者称为纵向变量序列(个体)的多次测量。
所以,面板数据(panel data)也称时间序列截面数据(time series and cross section data)或混合数据(pool data)。
面板数据示意图见图1。
面板数据从横截面(cross section)看,是由若干个体(entity, unit, individual)在某一时点构成的截面观测值,从纵剖面(longitudinal section)看每个个体都是一个时间序列。
图2是1978~2005年中国各省级地区消费性支出占可支配收入比率序列图。
图2 1978-2005年中国各省级地区消费性支出占可支配收入比率序列图(价格平减过)面板数据用双下标变量表示。
例如y i t, i = 1, 2, …, N; t = 1, 2, …, Ti对应面板数据中不同个体。
N表示面板数据中含有N个个体。
t对应面板数据中不同时点。
T表示时间序列的最大长度。
若固定t不变,y i ., ( i = 1, 2, …, N)是横截面上的N个随机变量;若固定i不变,y. t, (t = 1, 2, …, T)是纵剖面上的一个时间序列(个体)。
这里所讨论的面板数据主要指时期短而截面上包括的个体多的面板数据。
利用面板数据建立模型的好处是:(1)由于观测值的增多,可以增加估计量的抽样精度。
(2)对于固定效应回归模型能得到参数的一致估计量,甚至有效估计量。
(3)面板数据建模比单截面数据建模可以获得更多的动态信息。
例如1990-2000年30个省份的农业总产值数据。
固定在某一年份上,它是由30个农业总产值数字组成的截面数据;固定在某一省份上,它是由11年农业总产值数据组成的一个时间序列。
补充回答:面板数据比时间序列和截面数据复杂多了。
首先你得对模型的设定和数据的选取有个大概的确定(多少年?多少个截面?多少个变量?),然后是建立POOL数据,首先做F检验,看看应该是用混合数据模型、变截距模型还是变系数模型,当然,根据你研究的目的,也可以变系数来研究不同截面之间是否在某个变量上存在一致性。
采用固定效应还是随机效应要做豪斯曼检验,不过一般用固定效应就可以。
模型选定就是回归了,可以用OLS也可以用GLS,DW值不好的,可以在模型中加AR(N)进行修正。
模型是要不断的尝试和修改的,最后取一个最符合要求的。
使用Eviews软件对精神卫生门诊人次进行ARIMA模型预测我不知道你们考试和我们一样发。
我学习的是英文版,不知道你们是不是。
第一步,file中选new,新建workfile。
第二步,data y录入数据,录入自变量时,就是data x1,后面的依此类推打开以后里面和excel差不多,如果打不进去,你看看是不是调整到了编辑界面,在data的窗口上面一排按钮里面有个+/-Edit,按一下就可以切换。
第三步,普通最小二乘法OLSls y c x1 x2 x3...回车后出现个参数的估计值,还有判定系数,T、F检验之类的东西。
邹检验:在此OLS窗口中,通过上方view中stability tests的第一个chow breakpoint test,可以进行邹检验,里面输入第二组数据的第一个个数,如一共88个数据,现在邹检验分成两组,就输入45。
里面的F检验数值可以判定是否通过邹检验。
异方差性检验:也在view中residual tests 最后两个white heteroskedasticity(cross terms)或者(no cross terms),就是方程有没有交叉项。
选择下就出来F的结果了,然后判定下。
如果有异方差性,也就是F>c,再怀特方法,还是在OLS窗口上方的estimate,按一下,弹出来的窗口右侧勾勾和叉叉下面选择option,在heteroskedasticity 前面打勾,选下面的white,确定,再之前的窗口再确定,之后会出来调整过的方程。
(1)生成POOL序列如下:描述性统计如下:
转化成表格如下:
Mean
Median Maximum Minimum Std. Dev.
WAGE? 80.65833 85.35 123.2 37.2 22.26609 UNEM? 8.158333 7.65 11.8 4 2.037138
从回归结果来看,小时工资的系数为负,且其t统计量对应的p值小于5%,因此在5%的显著性水平,其对失业率有显著的负向影响。
这点可能是随着小时工资的提高,个人倾向于寻求就业,从而使失业率降低,具体而言,小时工资每提高1美元,失业率平均下降0.03707%。
而由不同国家的截距差异可以看出,在小时工资不变的情况下,美国的失业率最低,加拿大次之,英国最高,同时也注意到不同年份也存在一定的差异,这可能是由于经济发展正常的波动。
个体时间双随机变截距情况下,小时工资的系数为负且通过1%的显著性检验,即小时工资的提高可以显著降低失业率,这可能是随着小时工资的提高,劳动者更倾向于参与劳动,从而对失业率有显著的削弱作用,具体而言,小时工资每增加1美元,失业率平均下降0.04586%。
此外,不同国家的失业率在小时工资不变的情况下,也有所差异,美国最低,加拿大次之,最高的是英国,同时年份的不同也是失业率差异的因素,这可能与经济周期发展有关。
(4)在随机效应的基础上进行Hausman检验,结果如下:
从Hausman检验的结果来看,针对个体随机变截距效应的原假设,p值大于5%,因此不拒绝原假设,即个体随机效应是存在的,而针对时间随机效应变截距的原假设,p值大于5%,因此也不拒绝原假设,时间随机效应也是存在的,针对同时存在个体时间双随机变截距的原假设,p值也是大于5%,因此,模型在设定上应该为个体时点双随机模型。
第8讲用面板数据模型预测1.面板数据定义时间序列数据或截面数据都是一维数据。
时间序列数据是变量按时间得到的数据;截面数据是变量在固定时点的一组数据。
面板数据是同时在时间和截面上取得的二维数据。
面板数据也可以定义为相同截面上的个体在不同时点的重复观测数据或者称为纵向变量序列(个体)的多次测量。
所以,面板数据(panel data)也称时间序列截面数据(time series and cross section data)或混合数据(pool data)。
面板数据示意图见图1。
面板数据从横截面(cross section)看,是由若干个体(entity, unit, individual)在某一时点构成的截面观测值,从纵剖面(longitudinal section)看每个个体都是一个时间序列。
图1 N=15,T=50的面板数据示意图图2是1978~2005年中国各省级地区消费性支出占可支配收入比率序列图。
图2 1978-2005年中国各省级地区消费性支出占可支配收入比率序列图(价格平减过)面板数据用双下标变量表示。
例如y i t, i = 1, 2, …, N; t = 1, 2, …, Ti对应面板数据中不同个体。
N表示面板数据中含有N个个体。
t对应面板数据中不同时点。
T表示时间序列的最大长度。
若固定t不变,y i ., ( i = 1, 2, …, N)是横截面上的N个随机变量;若固定i不变,y. t, (t = 1, 2, …, T)是纵剖面上的一个时间序列(个体)。
这里所讨论的面板数据主要指时期短而截面上包括的个体多的面板数据。
利用面板数据建立模型的好处是:(1)由于观测值的增多,可以增加估计量的抽样精度。
(2)对于固定效应回归模型能得到参数的一致估计量,甚至有效估计量。
(3)面板数据建模比单截面数据建模可以获得更多的动态信息。
例如1990-2000年30个省份的农业总产值数据。
固定在某一年份上,它是由30个农业总产值数字组成的截面数据;固定在某一省份上,它是由11年农业总产值数据组成的一个时间序列。
面板数据由30个个体组成。
共有330个观测值。
对于面板数据y i t, i = 1, 2, …, N; t = 1, 2, …, T,如果每个个体在相同的时期内都有观测值记录,则称此面板数据为平衡面板数据(balanced panel data)。
若面板数据中的个体在相同时期内缺失若干个观测值,则称此面板数据为非平衡面板数据(unbalanced panel data)。
案例1:1996-2002年中国东北、华北、华东15个省级地区的居民家庭固定价格的人均消费(CP)和人均收入(IP)关系研究(file:5panel02)1996-2002年中国东北、华北、华东15个省级地区的居民家庭固定价格的人均消费(CP)和人均收入(IP)数据见file:panel02。
数据是7年的,每一年都有15个数据,共105组观测值。
人均消费和收入两个面板数据都是平衡面板数据,各有15个个体。
人均消费面板数据按个体连线见图3,按截面连线见图4。
人均收入面板数据按个体连线见图5,按截面连线见图6。
图3 15个省级地区的人均消费序列(个体)(file:5panel02)图4 7个人均消费横截面数据(含15个地区)(每条连线表示同一年度15个地区的消费值)图5 15个省级地区的人均收入序列(个体)(file:5panel02)图6 7个人均收入横截面数据(含15个地区)(每条连线表示同一年度15个地区的收入值)用CP表示消费,IP表示收入。
AH, BJ, FJ, HB, HLJ, JL, JS, JX, LN, NMG, SD, SH, SX, TJ,ZJ 分别表示安徽省、北京市、福建省、河北省、黑龙江省、吉林省、江苏省、江西省、辽宁省、内蒙古自治区、山东省、上海市、山西省、天津市、浙江省。
2000300040005000600070008000900010000110000400080001200016000IP(1996-2002)CPAH CPBJ CPFJ CPHB CPHLJ CPJL CPJS CPJX CPLN CPNMG CPSD CPSH CPSX CPTJ CPZJ图7 人均消费对收入的面板数据散点图(15个时间序列叠加)200040006000800010000120002000400060008000100001200014000IP(1996-2002)CP1996CP1997CP1998CP1999CP2000CP2001CP2002图8 人均消费对收入的面板数据散点图(7个截面叠加)15个地区7年人均消费对收入的面板数据散点图见图7和图8。
图7中每一种符号代表一个省级地区的7个观测点组成的时间序列。
相当于观察15个时间序列。
图8中每一种符号代表一个年度的截面散点图(共7个截面)。
相当于观察7个截面散点图的叠加。
为了观察得更清楚,图9给出北京和内蒙古1996-2002年消费对收入散点图。
从图中可以看出,无论是从收入还是从消费看内蒙古的水平都低于北京市。
内蒙古2002年的收入与消费规模还不如北京市1996年的大。
图10给出该15个省级地区1996和2002年的消费对收入散点图。
6年之后15个地区的消费和收入都有了相应的提高。
图9 北京和内蒙古1996-2002年消费对收入散点图 图10 1996和2002年15个地区的消费对收入散点图2.面板数据模型分类用面板数据建立的模型通常有3种,即混合回归模型、固定效应回归模型和随机效应回归模型。
2.1 混合回归模型(Pooled model )。
如果一个面板数据模型定义为, y it = α + X it 'β +εit , i = 1, 2, …, N ; t = 1, 2, …, T (1) 其中y it 为被回归变量(标量),α表示截距项,X it 为k ⨯1阶回归变量列向量(包括k 个回归量),β为k ⨯1阶回归系数列向量,εit 为误差项(标量)。
则称此模型为混合回归模型。
混合回归模型的特点是无论对任何个体和截面,回归系数α和β都相同。
如果模型是正确设定的,解释变量与误差项不相关,即Cov(X it ,εit ) = 0。
那么无论是N →∞,还是T →∞,模型参数的混合最小二乘估计量(Pooled OLS )都是一致估计量。
2.2 固定效应回归模型(fixed effects regression model )。
固定效应模型分为3种类型,即个体固定效应回归模型、时点固定效应回归模型和个体时点双固定效应回归模型。
下面分别介绍。
2.2.1个体固定效应回归模型(entity fixed effects regression model ) 如果一个面板数据模型定义为, y it = αi + X it 'β +εit , i = 1, 2, …, N ; t = 1, 2, …, T (3) 其中αi 是随机变量,表示对于i 个个体有i 个不同的截距项,且其变化与X it 有关系;X it 为k ⨯1阶回归变量列向量(包括k 个回归量),β为k ⨯1阶回归系数列向量,对于不同个体回归系数相同,y it 为被回归变量(标量),εit 为误差项(标量),则称此模型为个体固定效应回归模型。
个体固定效应模型(3)的强假定条件是,E(εit ∣αi , X it ) = 0, i = 1, 2, …, Nαi 作为随机变量描述不同个体建立的模型间的差异。
因为αi 是不可观测的,且与可观测的解释变量X it 的变化相联系,所以称(3)式为个体固定效应回归模型。
个体固定效应回归模型也可以表示为y it = α1 D 1 + α2 D 2 + … +αN D N + X it 'β +εit , t = 1, 2, …, T (4) 其中D i =⎩⎨⎧= 其他,,个个体如果属于第,,0 ..., ,2 ,1,1N i i注意:(1)在EViews5.0输出结果中αi 是以一个不变的常数部分和随个体变化的部分相加而成。
(2)在EViews 5.0以上版本个体固定效应对话框中的回归因子选项中填不填c 输出结果都会有固定常数项。
个体固定效应回归模型的估计方法有多种,首先设法除去αi 的影响,从而保证β估计量的一致性。
(详见第3节,面板数据模型估计方法。
)下面解释设定个体固定效应回归模型的原因。
假定有面板数据模型 y it = β0 + β1 x it +β2 z i +εit , i = 1, 2, …, N ; t = 1, 2, …, T (5) 其中β0为常数,不随时间、截面变化;z i 表示随个体变化,但不随时间变化的难以观测的变量。
以案例1为例,省家庭平均人口数就是这样的一个变量。
对于短期面板来说,这是一个基本不随时间变化的量,但是对于不同的省份,这个变量的值是不同的。
上述模型可以被解释为含有N 个截距,即每个个体都对应一个不同截距的模型。
令αi = β0 +β2 z i ,于是(5)式变为y it = αi + β1 x it +εit , i = 1, 2, …, N ; t = 1, 2, …, T (6) 这正是个体固定效应回归模型形式。
对于每个个体回归函数的斜率相同(都是β1),截距αi 却因个体不同而变化。
可见个体固定效应回归模型中的截距项αi 中包括了那些随个体变化,但不随时间变化的难以观测的变量的影响。
αi 是一个随机变量。
因为z i 是不随时间变化的量,所以当对个体固定效应回归模型中的变量进行差分时,可以剔除那些随个体变化,但不随时间变化的难以观测变量的影响,即剔出αi 的影响。
以案例1(file:5panel02)为例得到的个体固定效应模型估计结果如下: 输出结果的方程形式是t y 1ˆ= γˆ安徽+1ˆβ x 1t = (515.6 - 36.3) + 0.70 x 1t (55.0)t y 2ˆ= γˆ北京+1ˆβx 2t = (515.6 + 537.6) + 0.70 x 2t 。
(55.0)t y 15ˆ= γˆ浙江+1ˆβx 15t = (515.6 + 198.6) + 0.70 x 15t (55.0)R 2 = 0.99, SSE r = 2270386, t 0.05 (88) = 1.98从结果看,北京、上海、浙江是自发消费(消费函数截距)最大的3个地区。
图11 EViwes5.1个体固定效应回归模型的估计结果2.2.2 时点固定效应回归模型(time fixed effects regression model ) 如果一个面板数据模型定义为,y it = γt + X it 'β +εit , i = 1, 2, …, N (7) 其中γt 是模型截距项,随机变量,表示对于T 个截面有T 个不同的截距项,且其变化与X it 有关系;y it 为被回归变量(标量),εit 为误差项(标量),满足通常假定条件。