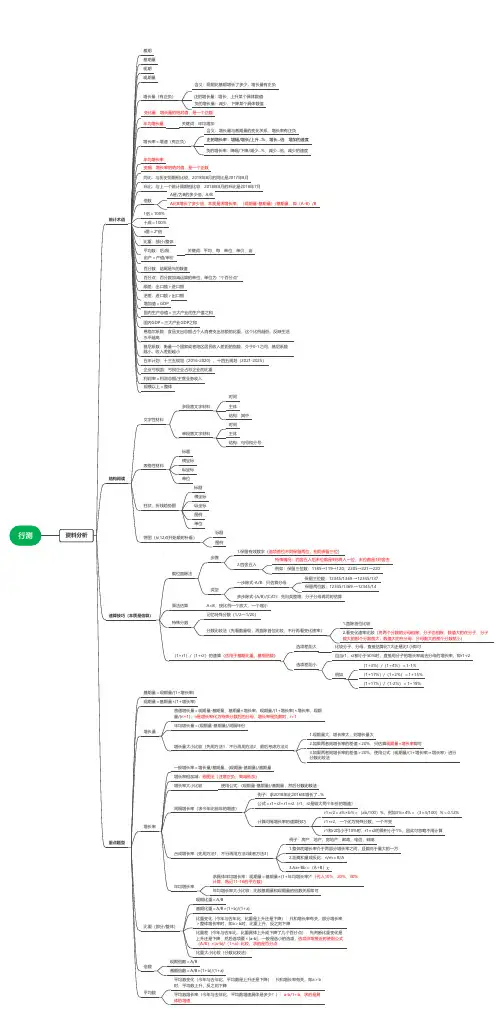
资料分析思维导图

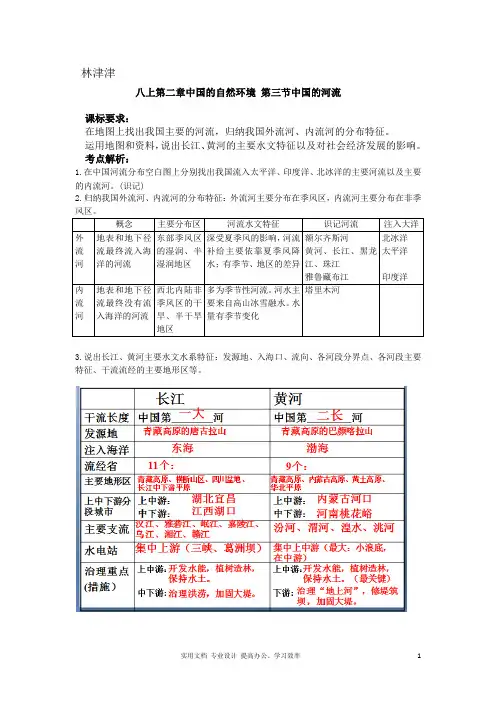
林津津八上第二章中国的自然环境第三节中国的河流课标要求：在地图上找出我国主要的河流，归纳我国外流河、内流河的分布特征。

运用地图和资料，说出长江、黄河的主要水文特征以及对社会经济发展的影响。

考点解析：1.在中国河流分布空白图上分别找出我国流入太平洋、印度洋、北冰洋的主要河流以及主要的内流河。

(识记)2.归纳我国外流河、内流河的分布特征：外流河主要分布在季风区，内流河主要分布在非季3.说出长江、黄河主要水文水系特征：发源地、入海口、流向、各河段分界点、各河段主要特征、干流流经的主要地形区等。

4.能对比不同河流水文特征，主要包括：流量、汛期、含沙量、结冰期、补给类型。

5.分析河流对社会经济发展思维导图：以外流河为主：黄河:长江：典型例题：1.读右图，回答以下题目：（1）图1中，关于中国内、外流区说法正确的是（ ） A.外流区中有内流区 B.外流区主要在非季风区 C.外流区面积更大 D.内流区离海更近 （2）河流③和④相比（ ）A. ③泥沙含量更多B. ③流量更小C. ③结冰期更长D. ③汛期更长（3）图2中各河流流量大小最有可能代表的河流是（ ） A. ④、①、⑨、③ B. ⑨、①、④、③ C. ③、④、①、⑨ D. ①、④、⑨、③（4）位于中国南方和北方的分界线是（ ） A. ④ B. ② C. ⑨ D. ⑧【命题意图】让学生通过阅读中国水系图和四条河流流量变化示意图，了解中国河流的分布特征、水文特征。

命题依据课程标准，以能力立意为导向，体现地理学科的特点。

整题的顺序先易后难，结构平衡，考点多样，利于学生正常发挥。

【试题解析】第1小题，考查内外流区的分布特征，难度较低，让学生通过读图完成相关内容，旨在培养学生运用地图的能力。

第2小题考查长江、黄河的水文特征对比，代表了秦岭-淮河南北的河流，难度中等，旨在学生应用能力的提升，进而培养学生的地理思维能力。

第3小题考查中国东部季风区河流的补给来自降水，通过中国南北降水的对比分析得出结果，难度较高，体现学习生活有用的地理，可体现学生的地理综合分析能力。

思维导图+重点知识梳理二次根式加、减、乘、除运算二次根式性质最简二次根式2 = 0 a a a ≥()()()()==-⎧⎪⎨⎪⎩200＜a a a a a a ≥ ⋅⋅ = 0 0 a b a b a b (≥, ≥)()00＞，bba b a a ≥= 0 0a a ≥≥()【例题展示】 已知a ，b 为等腰三角形的两条边长，且a，b 满足 ，求此三角形的周长．3264b a a =-+-+解：由题意得∴a =3，∴b =4.当a 为腰长时，三角形的周长为3+3+4=10；当b 为腰长时，三角形的周长为4+4+3=11．30260a a -⎧⎨-⎩≥，≥，【例题展示】 化简：(1)16;2(2)(5)-；解：2164 4.==22(2)(5)5 5.-==210;-2(3.14).-π()22111101010=10.----2(3.14) 3.14= 3.14.---πππ ，而3.14＜π，要注意a 的正负性.注意2a a =32327+63---（）；06(2)20163+312.2--（）-63336=--+解：(1)原式33.=-(2)原式333=--3 2.=-【例题展示】计算：有绝对值符号的，同括号一样，先去绝对值，注意去掉绝对值后，得到的数应该为正数.归纳勾股定理　直角三角形边长的数量关系 勾股定理的逆定理 直角三角形的判定 互逆定理勾股定理【例题展示】 有一个圆柱形油罐，要以A 点环绕油罐建梯子，正好建在A 点的正上方点B 处，问梯子最短需多少米(已知油罐的底面半径是2 m ，高AB 是5 m ，π取3）?AB AB A 'B '解：油罐的展开图如图，则AB '为梯子的最短距离.∵AA '=2×3×2=12, A 'B '=5,∴AB '=13. 即梯子最短需13米.【例题展示】 如图，南北方向PQ 以东为我国领海，以西为公海，晚上10时28分，我边防反偷渡巡逻101号艇在A 处发现其正西方向的C 处有一艘可疑船只正向我沿海靠近，便立即通知在PQ 上B 处巡逻的103号艇注意其动向，经检测，AC =10海里，BC =8海里，AB=6海里，若该船只的速度为12.8海里/时，则可疑船只最早何时进入我领海？东北P AB C Q D分析：根据勾股定理的逆定可得△ABC 是直角三角形，然后利用勾股定理的逆定理及直角三角形的面积公式可求PD ，然后再利用勾股定理便可求CD .解：∵AC =10，AB =6，BC =8，∴AC 2=AB 2+BC 2，即△ABC 是直角三角形.设PQ 与AC 相交于点D ，根据三角形面积公式有 BC·AB= AC·BD ，即6×8=10BD ，解得BD=在Rt △BCD 中，2222248 6.4().5CD BC BD ⎛⎫=-=-= ⎪⎝⎭海里又∵该船只的速度为12.8海里/时，6.4÷12.8=0.5（小时）=30（分钟），∴需要30分钟进入我领海，即最早晚上10时58分进入我领海.东北P A B C QD 24.512125种判定方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等平行四边形、矩形、菱形、正方形之间的关系平行四边形【例题展示】如图，已知O是平行四边形ABCD的对角线的交点，AC=24，BD=18，AB=16，求△OCD的周长及AD边的取值范围．解：由题意得OA=OC=12，OB=OD=9，CD=AB=16,∴△OCD的周长为12+9+16=37.在△ACD中，24-16＜AD＜24+16，∴8＜AD＜40；在△ABD中，18-16＜AD＜18+16，∴2＜AD＜34；在△AOD中，12-9＜AD＜12+9，∴3＜AD＜21．综上所述，AD的取值范围应是8＜AD＜21．【例题展示】 如图，点C是AB的中点，AD=CE，CD=BE．（1）求证：△ACD≌△CBE；（2）连接DE，求证：四边形CBED是平行四边形．证明：（1）∵点C是AB的中点，∴AC=BC.在△ADC与△CEB中，AD＝CE , CD＝BE , AC＝BC ,∴△ADC≌△CEB（SSS），（2）∵△ADC≌△CEB，∴∠ACD=∠CBE，∴CD∥BE.又∵CD=BE，∴四边形CBED是平行四边形．【例题展示】 如图，在△ABC中，AB＝AC，E为AB的中点，在AB的延长线上取一点D，使BD＝AB，求证：CD＝2CE.证明：取AC的中点F，连接BF.∵BD＝AB，∴BF为△ADC的中位线，∴DC＝2BF.∵E为AB的中点，AB＝AC，∴BE＝CF，∠ABC＝∠ACB.F∵BC＝CB，∴△EBC≌△FCB,∴CE＝BF，∴CD＝2CE .【例题展示】 如图，在△ABC中，AB＝AC，AD⊥BC，垂足为D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为E，求证：四边形ADCE为矩形．证明：在△ABC中，AB＝AC，AD⊥BC，∴∠BAD＝∠DAC，即∠DAC＝ ∠BAC.又∵AN是△ABC外角∠CAM的平分线，∴∠MAE＝∠CAE＝ ∠CAM,∴∠DAE＝∠DAC＋∠CAE ＝ (∠BAC＋∠CAM)＝90°.又∵AD⊥BC，CE⊥AN，∴∠ADC＝∠CEA＝90°,∴四边形ADCE为矩形．1 212 12【例题展示】 如图，在△ABC中，∠B＝90°，AB＝6cm，BC＝8cm.将△ABC沿射线BC方向平移10cm，得到△DEF，A，B，C的对应点分别是D，E，F，连接AD.求证：四边形ACFD是菱形．证明：由平移变换的性质得CF＝AD＝10cm，DF＝AC.∵∠B＝90°，AB＝6cm，BC＝8cm，∴AC＝DF＝AD＝CF＝10cm，∴四边形ACFD是菱形．()22226810cm. AC AB BC∴=+=+=某些运动变化 的现实问题 函数建立函数模型定义自变量取值范围 表示法 一次函数 y =kx +b (k ≠0)应用图象：一条直线性质：k ＞0，y 随x 的增大而增大 k ＜0，y 随x 的增大而减小数形结合一次函数与方程（组）、 不等式之间的关系一次函数【例题展示】小明所在学校与家距离为2千米，某天他放学后骑自行车回家，行驶了5分钟后，因故停留10分钟，继续骑了5分钟到家.如图，能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系图象D的是（ ）【例题展示】 已知直线l与直线y=-2x平行，且与y轴交于点(0，2)，求直线l的解析式.解：设直线l为y=kx+b, ∵l与直线y=-2x平行，∴k= -2.又∵直线过点（0，2），∴2=-2×0+b,∴b=2,∴直线l的解析式为y=-2x+2.【例题展示】小明将父母给的零用钱按每月相等的数额存在储蓄盒内，准备捐给希望工程，盒内钱数y （元）与存钱月数 x （月）之间的关系如图所示，根据下图回答下列问题：（1）求出y 关于x 的函数解析式.（2）根据关系式计算，小明经过几个月才能存够200元？4080120y /元x /月12345o解: (1)设函数解析式为y =kx ＋b ，由图可知图象过(0，40),(4，120)，∴这个函数的解析式为y =20x +40.(2)当y =200时，20x +40=200, 解得x =8，∴小明经过8个月才能存够200元.解得20,40,k b =⎧⎨=⎩∴{040,4120,k b k b ⨯+=+=4080120y /元x /月12345o数据的集中趋势数据的波动程度 方差用样本平均数估计总体平均数 用样本方差估计总体方差平均数 中位数 众 数 用样本估计总体数据的分析　数据收集—数据整理—数据描述—数据分析 【例题展示】 已知一组数据10，10，x，8(由大到小排列)的中位数与平均数相等，求x值及这组数据的中位数.解：∵10，10，x，8的中位数与平均数相等∴ (10+x)÷2＝ (10+10+x+8)÷4∴x＝8(10+x)÷2＝9∴这组数据的中位数是9.【例题展示】.五个数1，3，a，5，8的平均数是4，则a3 5.6=_____，这五个数的方差_____.。

目录Contents
第一篇 咬文嚼字需谨慎 一言一语总关情 (1)
言语理解与表达思维导图 (1)
第二篇 判断问题快准狠 推理之中定乾坤 (4)
判断推理思维导图 (4)
第三篇 数量问题不抽象 把握关系要得当 (7)
数量关系思维导图 (7)
第四篇 资料分析抓重点 省时省力找答案 (8)
资料分析思维导图 (8)
第一篇 咬文嚼字需谨慎 一言一语总关情言语理解与表达思维导图
第二篇 判断问题快准狠 推理之中定乾坤
判断推理思维导图
第三篇 数量问题不抽象 把握关系要得当
数量关系思维导图
第四篇 资料分析抓重点 省时省力找答案
资料分析思维导图
思维导图——职测A类
思维导图——职测A类。

绿色植物与生物圈的水循环
主题单元学习目标
知识与技能：说明植物的生活需要水的原因，水对植物分布的影响，解读数据的方法，说出根毛对植物吸水的意义和水在植物体内的运输途径。

运用有关绿色植物吸收水和运输器官的特点，了解绿色植物的蒸腾作用，描述气孔的组成及开闭原理，描述绿色植物在生物圈水循环中的重要作用。

过程与方法：通过测定植物的蒸腾作用和观察叶表皮气孔的实验，培养分析和综合的能力、画图能力以及实验探究能力。

培养学生运用知识解决实际问题的能力。

情感态度与价值观：爱护植物生活的水源，保护植物，涵养水源。

认同绿色植物对于维持生物圈中水循环的重要意义，自觉形成爱护绿色植物的美好情感初步形成节约用水，保护森林的意识。

欧洲西部情，激发学生的学习兴趣，1、看了这些图片，你最大的感受是什么？2、图片中涉及到哪些国家？这些国家都位于哪个大洲？他们都位于我们今天要学习的地区——欧洲西部。

活动二：讲授新课：去欧洲西部游学，出发前同学们只申请了德国和英国两个国家的签证，游学时却游走了多个国家，畅行无阻！乘坐飞机非常便捷，而且，有些国家之间还提供铁路通票，一张票在手，就可以走遍17国。

在乘坐某些国家的渡轮、缆车和公共汽车时还可以享受免费或折扣的优惠！在各国消费的时侯，也都大多使用同一种货币。

学生交流上述现象反映了什么？活动三：自主学习，合作探究学习任务一：认识欧洲西部的位置、范围、国家1、自主学习读图2-25结合地图册p28-29地图,回答：1）、欧洲西部地处南北半球、东西半球的哪两个半球？2）、欧洲西部的北、南、西分别濒临什么海或洋？3）、欧洲西部最南端的纬度大约是多少？最北端的纬度大约是多少？推测在五带中大部分处于什么温度带？4）、在“欧洲西部地形图”上找出欧洲西部的主要岛屿( 冰岛、大不列颠岛）、半岛（斯堪的纳维亚半岛、伊比利亚半岛、亚平宁半岛、巴尔干半岛）、海峡(英吉利海峡、直布罗陀海峡）、北海、波罗的海、比斯开湾。

5）、在欧洲西部的国家图中找到：英国、法国、德国、丹麦、西班牙、意大利、瑞士、奥地利、挪威等国，试着找出英国、法国、德国、意大利等国的首都。

2、小组交流学生小组交流，欧洲西部的地理位置特点以上问题并提出疑难3、阅读p53阅读材料，了解欧洲联盟的总部所在地、简称、统一货币、欧洲联盟在世界的地位活动四:快乐抢答：1、欧洲联盟的简称是什么？2、欧洲联盟的总部设在哪里？3、欧洲联盟统一使用的货币是什么?4、说明欧洲联盟在世界的地位教师介绍欧盟的作用任务二：雄厚的经济实力读图2-26思考：人均国民生产总值世界前十位的国家，欧洲西部占据了几个？说明了什么问题？小组合作探究：分小组考察欧洲西部的工业、农业、交通、部分国家的特色产业以小组为单位展示欧洲西部的工业、农业、交通、部分国家的特色产业。

∙截位直除o截谁▪一步除法：建议只截分母。

▪多步计算：建议上下都截。

o截几位▪选项差距大：截两位∙选项首位不同。

∙首位相同次位差大于首位。

▪选项差距小：截三位∙首位相同且次位差小于等于首位。

∙分数比较o一大一小直接看▪根据分子比大小，分子大的分数大，分子小的分数小。

o同大同小比速度▪上下直接除，左右看变化谁快谁牛气，慢的看成1。

∙快速找数o文字材料▪标记段落主题词，与题干进行匹配，注意相近词、时间、单位等。

o表格材料▪横纵目标，标题，单位，备注。

o图形材料▪标题，单位，图例。

o综合材料▪不同类型材料之间的关系，材料结构。

∙基期与现期o基期量▪识别：求前面某个时期的量。

▪公式：基期=现期-增长量：基期=现期/(1+r)▪速算：|r|>5大截位直除，|r|≤5小化除为乘。

▪基期和差：先用现期和正负排除再计算。

o现期量▪识别：求后面某个时期的量。

▪公式：现期=基期+增长量；现期=基期*（1+r）。

▪速算：截位计算，特殊数字。

∙增长率o普通增长率▪题型识别：增长/下降后%；成；倍；增长最快/慢。

▪解题方法：给百分点，直接加减；无百分点，r=增长量+基期量。

▪速算技巧：截位直除法；分数比较法。

o特殊增长率▪间隔增长率∙中间隔一年的增长率，今年与前年∙r=r1+r2+r1*r2,速算考虑r1*r2是否忽略。

▪年均增长率∙计算：（1+r）的n次方=现期+基期；居中代入。

∙比较：直接看现期+基期（n相同）▪混合增长率∙部分增速与整体增速之间的关系。

∙居中但不正中；偏向基期较大的；增速差与基期成反比。

∙增长量o计算▪识别：增长+单位（人/元/吨）。

▪公式：增长量=现期-基期=基期*r==现期r/(1+r)▪速算：∙百分数化分数：近似转化，倍数转化，取中转化。

∙若|r|≈1/n，增长量=现期/（n+1）；下降量=现期/（n-1）o比较▪识别：增长量多/少▪速算∙给出每年数据：直接两两相减，柱状图还可用直尺标注。

北师大版六年级数学数据处理思维导图+知识梳理+例题精讲+易错专练一、思维导图二、知识点梳理知识点一：扇形统计图1.扇形统计图。

扇形统计图是以一个圆作为总体，表示各部分量占单位“1”的量。

根据各部分量所占的百分比，用大小不同的扇形在这个圆中表示部分量，所以称为扇形统计图。

扇形所占的百分比越大，扇形的面积就越大；扇形所占的百分比越小，扇形的面积就越小。

2.扇形统计图的特点：能清楚地看出部分与整体之间的关系，也就是部分占整体的百分比的大小。

3.从扇形统计图中获取信息的方法：先与整体比较，看各部分占整体的百分比是多少，再看各部分之间谁占的百分比大，在此基础上仔细分析，得出结论。

知识点二：统计图的选择选择统计图的方法：条形统计图便于看出数据的多少；折线统计图便于看出数据的变化趋势，也能看出数据的多少；扇形统计图能清楚地看出部分与整体及部分与部分之间的关系。

知识点三：身高的情况－分段整理数据并解决问题分段整理、分析数据的方法：可以先把数据排列，并根据需要把数据按一定的标准分段整理，再用统计图描述数据，最后对数据作出全面的分析，并解决问题。

知识点四：身高的变化－统计图表的填补1.绘制复式折线统计图的方法和步骤：绘制复式折线统计图的方法和步骤与绘制单式折线统计图的方法相同，只是在同一统计图中用两种或两种以上的线表示不同的量，并要标明图例。

2.观察统计图的方法：通过运用横向观察、纵向观察、对比观察等多种方法，从中获取更多信息，提出并解决问题及作出合理的预测。

3.比较两组数据的方法：（1）比较两组数据中的最大值或最小值；（2）比较两组数据的平均值；（3）把两组数据分段比较。

三、例题精讲考点一：扇形统计图1．这是一款奶粉的成分含量情况统计图，看图回答下列问题。

①蛋白质的含量占奶粉总量的（）%。

②如果蛋白质的含量是200g，那这款奶粉的总质量是（）g。

③乳糖的含量比乳脂的含量多（）%。

④请你提一个数学问题并解答。

2．如图，苹果的销量占水果总销量的( )%，香蕉的销量占总销量的( )%，香蕉的销量是125kg，则橙子的销量是( )kg，西瓜的销量是( )kg，这一天的水果总销量是( )kg。

初中生物《动物的运动和行为》单元教学设计以及思维导图2动物的运动和行为适用年八年级级所需时课内三课时，课外二课时(每周一课时)间主题单元学习概述:有关动物的运动和行为的知识对学生认识动物的本质特征非常重要，动物的行为是目前生物学研究中一个十分活跃的领域，动物行为的知识和人类生活和生产密切相关。

本单元提供了分析和实验用的素材，让学生开展探究性学习。

通过对素材的分析，教师引导学生认识动物行为形成的机理，理解行为形成的本质和意义。

本单元包括动物的运动和动物的行为两个专题。

(一)动物的运动重点:理解肌肉、关节与功能相适应的结构特点 ;理解动物运动对动物生存的意义;根据素材分析推理，进行探究性学习。

难点:运动是动物结构和功能的统一，运动是动物行为的具体表现。

(二)动物的行为教学重点:区分先天性行为和后天学习行为，使学生对一些动物行为判别;使学生能够阐明动物的行为对于动物生存的意义。

教学难点:使学生能区分先天性行为和后天学习行为;使学生懂得学习行为的复杂性和遗传性。

本单元通过学生学生通过课后分组制作模型的方式，使学生更好的认识运动系统的组成、各自得作用及相互关系。

课本中资料分析通过小组合作的方式，让学生学会区分动物的先天性行为和学习行为。

运用实验的方法探究动物的先天性行为和学习行为。

主题单元规划思维导图主题单元学习目标知识与技能:1、描述动物运动的结构基础。

2、概述结构和功能的统一性。

3、概述运动对动物生存的意义。

4、通过学习使学生能区别动物的先天性行为和后天学习行为。

5、通过学习使学生能阐明动物的行为对于动物生存的意义。

过程与方法:1、通过对运动系统组成的观察与学习，使学生能与生产实践相联系。

2、通过屈肘和伸肘动作的观察与思考，使学生把握事物的内在联系，确立辩证统一看问题思维观点。

3、通过模拟实验的制作，使学生具有能运用所学知识，尝试一些手工制作，培养探究实验动手操作能力、合作学习的能力和表达能力。

4、通过对动物行为的观察和研究，培养学生观察能力、分析能力。

目录
言语理解与表达思维导图 (3)
逻辑填空 (4)
概括类片段阅读——主旨理解题1 (5)
概括类片段阅读——主旨理解题2 (6)
细节类片段阅读 (7)
语句表达 (8)
篇章阅读 (9)
判断推理思维导图 (10)
图形推理——平面图形1 (11)
图形推理——平面图形2 (12)
图形推理——平面图形3 (13)
图形推理——空间重构 (14)
类比推理——横向辨析 (15)
类比推理——纵向辨析 (16)
定义判断 (17)
逻辑判断——基础知识1 (18)
逻辑判断——基础知识2 (19)
逻辑判断——形式逻辑1 (20)
逻辑判断——形式逻辑2 (21)
逻辑判断——论证逻辑1 (22)
逻辑判断——论证逻辑2 (23)
数量关系思维导图 (24)
数量关系——方法篇1 (25)
数量关系——方法篇2 (26)
数量关系——高频考点1 (28)
数量关系——高频考点3 (30)
数量关系——高频考点4 (31)
数量关系——高频考点5 (32)
数量关系——高频考点6 (33)
数量关系——高频考点7 (34)
资料分析思维导图 (36)
资料分析——速算技巧 (37)
资料分析——高频考点1 (38)
资料分析——高频考点2 (39)
资料分析——高频考点3 (40)
资料分析——高分必背 (41)
言语理解与表达思维导图
逻辑填空
细节类片段阅读
判断推理思维导图。