自由曲面设计之切面迭代法介绍

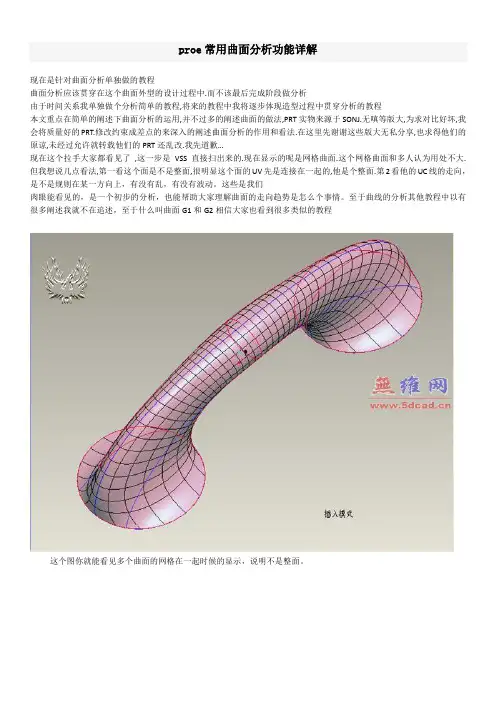
proe常用曲面分析功能详解现在是针对曲面分析单独做的教程曲面分析应该贯穿在这个曲面外型的设计过程中.而不该最后完成阶段做分析由于时间关系我单独做个分析简单的教程,将来的教程中我将逐步体现造型过程中贯穿分析的教程本文重点在简单的阐述下曲面分析的运用,并不过多的阐述曲面的做法,PRT实物来源于SONJ.无嗔等版大,为求对比好坏,我会将质量好的PRT.修改约束成差点的来深入的阐述曲面分析的作用和看法.在这里先谢谢这些版大无私分享,也求得他们的原谅,未经过允许就转载他们的PRT还乱改.我先道歉…现在这个拉手大家都看见了,这一步是VSS直接扫出来的.现在显示的呢是网格曲面.这个网格曲面和多人认为用处不大.但我想说几点看法,第一看这个面是不是整面,很明显这个面的UV先是连接在一起的,他是个整面.第2看他的UC线的走向，是不是规则在某一方向上，有没有乱，有没有波动。

这些是我们肉眼能看见的，是一个初步的分析，也能帮助大家理解曲面的走向趋势是怎么个事情。

至于曲线的分析其他教程中以有很多阐述我就不在追述，至于什么叫曲面G1和G2相信大家也看到很多类似的教程这个图你就能看见多个曲面的网格在一起时候的显示，说明不是整面。

网格曲面另一个重要作用呢就是观察收敛退化，也就是大家长说的3角面。

收敛退化是我们最不想看到的，但收敛点在那里呢，根据经验呢，比如说我这个，在做边界混合时候2条直线是一组，曲线是另一组，也就是退化点在2条直线相交的地方，但新手一般看见教程是跟着裁减那里的角，至于为什么是在哪个位置可能不是很清楚，就看下网格曲面吧剖面分析来说呢相对的要求比较高，原理呢很简单就是所选择的曲面面组和基准面相交的曲线的曲率梳，他不但能反映出单独曲面在截面基准面那里的曲率走向变化，还可以看出曲面和曲面接头处的曲率变化。

剖面分截面和高亮线2中分析。

截面分析的步骤呢我简单说下1，选取要在其上执行曲面分析的一个或多个曲面、面组、零件或所有模型曲面。

几何画板迭代详解迭代是几何画板中一个很有趣的功能，它相当于程序设计的递归算法。

通俗的讲就是用自身的结构来描述自身。

最典型的例子就是对阶乘运算可看作一下的定义：!(1)!(1)!(1)(2)!n n n n n n =⨯--=-⨯- 。

递归算法的特点是书写简单，容易理解，但是运算消耗内存较大。

我们先来了解下面这几个最基本的概念。

迭代：按一定的迭代规则，从原象到初象的反复映射过程。

原象：产生迭代序列的初始对象，通常称为“种子”。

初象：原象经过一系列变换操作而得到的象。

与原象是相对概念。

更具体一点，在代数学中，如计算数列1，3，5，7，9......的第n 项。

我们知道12n n a a -=+，所以迭代的规则就是后一项等于前一项加2。

以1作为原像，3作为初像，迭代一次后得到5，再迭代一次得到7，如此下去得到以下数值序列7 , 9，11, 13, 15......如图1.1所示。

在几何学中，迭代使一组对象产生一组新的对象。

图1.2中A 、B 、C 、D 、E 、F 、G ，各点相距1cm ，那么怎么由A 点和B 点得到其它各点呢？我们可以发现其中的规律就是从左到右，每一个点相当于前面一个点向右平移了1cm 。

所以我们以A 点作为原像，B 点作为初像，迭代一次得到B 点，二次为C 点，以此类推。

所以，迭代像就是迭代操作产生的象的序列，而迭代深度是指迭代的次数。

那么下面我们通过例子来进一步地了解迭代以及相关的概念。

几何画板中迭代的控制方式分为两种，一种是没有参数的迭代，另一种是带参数的迭代，我们称为深度迭代。

两者没有本质的不同，但前者需要手动改变迭代的深度，后者可通过修改参数的值来改变迭代深度。

我们先通过画圆的正n 边形这个例子来看一下它们的区别。

【例1】画圆的内接正7边形。

【分析】由正7边形的特征，我们知道，每一个点都相当于前面的点逆时针旋转360，抓住这个规律，我们可以用迭代功能来解决。

7【步骤】1.新建圆O，在圆O上任取一点A。

几何画板迭代详解之:迭代与分形几何佛山市南海区石门中学谢辅炬分形的特点是,整体与部分之间存在某种自相似性，整体具有多种层次结构。

分形图片具有无可争议的美学感召力，特别是对于从事分形研究的科学家来说。

欣赏分形之美当然也要求具有一定的科学文化知识，但相对而言，分形美是通俗易懂的.分形就在我们身边，我们身体中的血液循环管道系统、肺脏气管分岔过程、大脑皮层、消化道小肠绒毛等等都是分形，参天大树、连绵的山脉、奔涌的河水、漂浮的云朵等等,也都是分形。

人们对这些东西太熟悉了，当然熟悉不等于真正理解。

分形的确贴近人们的生活,因而由分形而来的分形艺术也并不遥远，普通人也能体验分形之美。

因为分形几何的迭代的原像一般不止一个，而且均为多映射迭代，为了叙述的方便，我们先作以下两个约定。

1.用（A，B，C）表示有顺序的两点A、B和C.2.(A,B,C)(D,E,F,),(G,H,I)表示A映射到D，B映射到D，C映射到F,然后添加映射A映射到G,B映射到H,C映射到I，如此类推。

【Sierpinski三角形】波兰著名数学家谢尔宾斯基在1915-1916年期间，为实变函数理论构造了几个典型的例子，这些怪物常称作“谢氏地毯"、“谢氏三角”、“谢氏海绵”、“谢氏墓垛"。

如今，几乎任何一本讲分形的书都要提到这些例子。

它们不但有趣,而且有助于形象地理解分形。

著名的Sierpinski三角形，它是很有代表性的线性分形，具有严格的自相似特点。

不断连接等边三角形的中点，挖去中间新的小三角形进行分割——-随着分割不断进行Sierpinski三角形总面积趋于零，总长度趋于无穷。

Sierpinski三角形在力学上也有实用价值，Sierpinski 三角形结构节省材料，强度高，例如埃菲尔铁塔的结构与它就很相似。

【步骤】1.在平面上任意画一个三角形ABC,取三边中点为D、E、F，连接DEF.2.新建参数n＝33.顺次选择B，C,A三点和参数n，作深度迭代,(B,C,A)(D,F,A)⇒。

迭代法详解迭代法（iteration）也称辗转法，是⼀种不断⽤变量的旧值递推出新值的解决问题的⽅法，迭代算法⼀般⽤于数值计算。

累加，累乘都是迭代算法的基础应⽤。

利⽤迭代法解题的步骤：1）确定迭代模型根据问题描述，分析出前⼀个（或⼏个）值与下⼀个值的迭代关系数学模型。

2）建⽴迭代关系式递推数学模型⼀般是带下标的字母，算法设计中要将其转化为“循环不变式”----迭代关系式，迭代关系式就是⼀个直接或间接地不断由旧值递推出新值的表达式，存储新值的变量称为迭代变量。

3）对迭代过程进⾏控制。

确定在什么时候结束迭代过程。

迭代过程是通过⼩规模问题的解逐步求解⼤规模问题的解，表⾯上看正好与递归相反，但也找到了⼤规模问题与⼩规模问题的关系。

本节的例⼦是⽤迭代完成的，也都可以⽤递归完成。

相信尝试后，定能体会到递归的简便之处。

1，递推法（recursion）是迭代算法的最基本表现形式。

⼀般来讲，⼀种简单的递推⽅法，就是从⼩规模的问题解出⼤规模问题的⼀种⽅法，也称其为“正推“。

如”累加“。

兔⼦繁殖问题：⼀对兔⼦从出⽣后第三个⽉开始，每⽉⽣⼀对兔⼦，⼩兔⼦每到第三个⽉有开始⽣兔⼦，问⼀年中每个⽉各有多少兔⼦？我们通常⽤的迭代：print(a,b)for(i=1;i<=10;i++){c=a+b; print(c); a=b; b=c;}另⼀种构造不变式的⽅法：1 2 3 4 5 6 7 8a b c=a+b a=b+c b=a+c c=a+b这样，⼀次循环其实是递推了三步，循环次数就要减少了。

#include<stdio.h>int main(){int i,a=1,b=1;int c;printf("%d %d ",a,b);for(i=1;i<=4;i++){c=a+b;a=b+c;b=c+a;printf("%d %d %d ",c,a,b); //注意输出顺序是c,a,b}}上⾯输出的共2+3*4=14项，这样的算法不太完美。

3.4 利用pro/e进行曲面造型曲面是一种没有厚度、质量、界限的薄膜。

一般对较规则的3D零件来说，实体特征提供了迅速且方便的造型建立方式。

但对复杂较高的造型设计而言，单单使用实体特征来建立3D 模型就显得很困难了，这是因为实体特征的造型建立方式较为固定化（如仅能使用拉伸、旋转、扫描、混合等方式来建立实体特征的造型），因此曲面特征应运而生，提供了非常弹性化的方式来建立单一曲面，然后将许多单一曲面集成为完整且没有间隙的曲面模型，通过封闭曲面转化为实体或者加厚曲面成为实体,来达到设计的目的。

它有别与实体造型,但是也和它息息相关。

曲面造型是一种用曲面表达实体形状的造型方法。

曲面特征的建立方式除了与实体特征相同的拉伸、旋转、扫描、混合等方式外，也可由点建立为曲线，再由曲线建立为曲面。

此外，曲面间也有很高的操作性，例如曲面的合并（merge），修剪（trim），延伸（extend）等（实体特征缺乏该类特征）。

由于曲面特征的使用较弹性化，因此其操作技巧性也较高3.4.1 基本曲面造型简介在造型的方法中,基本曲面由一下几种:填充、拉伸、旋转、扫描、混成。

第一种:填充曲面():以填充材料的方式构成曲面:先草绘封闭曲线,之后将在曲线边界内填充材料生成曲面,填充曲面一般为平面。

注意在pro/e中平面是有大小的,不像几何中的平面无限大,没有边界。

第二种:拉伸曲面(Extrude):拉伸曲面是指在绘图平面上的一条直线或曲线向垂直与绘图平面的一个或相对的两个方向拉伸说生成的曲面,平面是拉伸曲面最特殊的情况,结果类似与填充曲面。

第三种:旋转曲面(Revole):旋转曲面是指一条直线或曲线围绕一条中心轴线,按一定的角度旋所成的曲面(如图3-194所示图3-194第四种:扫描曲面(Sweep):扫描曲面是指一条直线或曲线(截面线)或直线或曲线(扫描路径)运动所生成的曲面,如图3-195所示。

图3-195第五种:混成曲面:混成曲面是由一系列直线或曲线的对应点串联所形成的曲面,混成曲面可根据对应点只见不同的数学过渡表达方式,可以是直线过渡,也可以是曲线过渡。

当前位置：模具学院首页>> Pro/E >> pro/E综合技巧>> ProE曲面设计方法总结及心得ProE曲面设计方法总结及心得2009-12-03 10:38:56 作者：未知来源：互联网浏览次数：437 文字大小：【大】【中】【小】在bound时，最好将破碎的边界近似结合后再邦面，虽然邦面后可能不能生成实体，可以将曲面同曲面延伸后生面实体1、curve和tanget chain的区别。

比如做两个连续的四边曲面，曲面A引用了curve1，则在创建曲面B时，最好引用A的tangent chain而不是其原始curv e。

因为尽管原理上A的边(tangent chain)即curve1，但在生成曲面后，它的边已经和原始c urve有了精度上的偏差。

所以为了保证曲面的连续性，应尽量选用tangent chain。

补充：在定义边界条件时，tangent chain无须选择曲面(因为本来就在曲面上)，而curv e则需选择相切曲面，也就是先前通过此curve创建的曲面。

(2)、变截面扫描时选项Pivot Dir(轴心方向)的理解。

首先把原始轨迹线看成无数个原点的组合，在任一原点处的截面参照为：原点、原点处的切线、以及过原点且与datum面垂直的直线(可以把它理解为创建point-on-plane轴)。

一个很好的例子是ice的鼠标面教程，以分模面作为变截面扫描的datum面，因此能保证任一扫描点处的脱模角。

(3)、创建连续的混合曲面，其curve要连续定义，以保证曲率连续;而曲面则可以先分开生成，再创建中间的连接面。

(4)，在通过点创建曲线时，可以用tweak进行微调，推荐选择基准平面进行二维的调节，然后再选择另一个基准进行调节，这样控制点就不会乱跑了。

(5)，如果曲面质量要求较高，尽可能用四边曲面。

(6)，扫描曲面尽可能安排在前面，因为它不能定义边界连接。

(7)，当出现>4边时，有时可以延长边界线并相交，从而形成四边曲面，然后再进行剪切处理。

常用算法——迭代法迭代法是一种常见的算法设计方法，它通过重复执行一定的操作来逐步逼近问题的解。

迭代法是一种简单有效的求解问题的方法，常用于求解数值问题、优化问题以及函数逼近等领域。

本文将介绍迭代法的基本概念、原理以及常见的应用场景。

一、迭代法的基本概念迭代法的思想是通过反复应用一些函数或算子来逐步逼近问题的解。

对于一个需要求解的问题，我们首先选择一个初始解或者近似解，然后通过不断迭代更新来逼近真实解。

迭代法的核心是找到一个递推关系，使得每次迭代可以使问题的解越来越接近真实解。

常见的迭代法有不动点迭代法、牛顿迭代法、梯度下降法等。

这些方法的求解过程都是基于迭代的思想，通过不断逼近解的过程来得到问题的解。

二、迭代法的原理迭代法的基本原理是通过不断迭代求解迭代方程的解，从而逼近问题的解。

迭代法的求解过程通常分为以下几个步骤：1.选择适当的初始解或者近似解。

初始解的选择对迭代法的收敛性和效率都有影响，一般需要根据问题的特点进行合理选择。

2.构建递推关系。

通过分析问题的特点，构建递推关系式来更新解的值。

递推关系的构建是迭代法求解问题的核心，它决定了每次迭代如何更新解的值。

3.根据递推关系进行迭代。

根据递推关系式，依次更新解的值，直到满足收敛条件为止。

收敛条件可以是解的变化小于一定阈值，或者达到一定的迭代次数。

4.得到逼近解。

当迭代停止时，得到的解即为问题的逼近解。

通常需要根据实际问题的需求来判断迭代停止的条件。

三、迭代法的应用迭代法在数值计算、优化问题以及函数逼近等领域有广泛的应用。

下面将介绍迭代法在常见问题中的应用场景。

1.数值计算：迭代法可以用于求解方程的根、解线性方程组、求解矩阵的特征值等数值计算问题。

这些问题的解通常是通过迭代的方式逼近得到的。

2.优化问题：迭代法可以应用于各种优化问题的求解，如最大值最小化、参数估计、模式识别等。

迭代法可以通过不断调整参数的值来逼近问题的最优解。

3.函数逼近：迭代法可以应用于函数逼近问题，通过不断迭代来逼近一个函数的近似解。

迭代算法简析----2bea2012-7165-11ec-a8f3-7cb59b590d7d算法设计之迭代法士兵们经常在进攻中交替掩护进攻。

如果数字轴上的点代表a和B的位置，且前面的数字大于后面的数字，则a>B和B>a交替出现。

但是现在假设军队里有一个胆小鬼，每个人都很照顾他。

每项指控都要让他跟进。

当前面的人占据一个新位置时，给他这个位置，然后其他人向前移动，占据一个新位置。

也就是说，a总是在B前面，a向前移动，B跟上，a把它的位置给B（即执行B=a的操作），然后a向前移动，占据一个新的位置，B跟上。

直到所有位置都被占据，前进结束。

两个数逐步逼近某一位置的方法称为迭代法。

迭代法也称辗转法，是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法（或者称为一次解法），即一次性解决问题。

迭代算法是用计算机解决问题的一种基本方法。

它利用计算机运算速度快、适合做重复性操作的特点，让计算机对一组指令（或一定步骤）进行重复执行，在每次执行这组指令（或这些步骤）时，都从变量的原值推出它的一个新值。

使用迭代算法解决问题需要以下三个方面：一、确定迭代变量。

在可以用迭代算法解决的问题中，至少存在一个直接或间接地不断由旧值递推出新值的变量，这个变量就是迭代变量。

二、建立一种反复的关系。

所谓的迭代关系是指如何从上一个值推导出一个变量的下一个值的公式（或关系）。

迭代关系的建立是解决迭代问题的关键，通常可以通过递归或反向方法来完成。

三、对迭代过程进行控制。

在什么时候结束迭代过程？这是编写迭代程序必须考虑的问题。

不能让迭代过程无休止地重复执行下去。

迭代过程的控制通常可分为两种情况：一种是所需的迭代次数是个确定的值，可以计算出来；另一种是所需的迭代次数无法确定。

对于前一种情况，可以构建一个固定次数的循环来实现对迭代过程的控制；对于后一种情况，需要进一步分析出用来结束迭代过程的条件。

最经典的迭代算法是欧几里德算法，用于计算两个整数a和B的最大公约数。

CATIA曲面设计理念全剖析（A面，B面，C面）2009-05-04 19:47关于做曲面，谈谈一点心得。

我觉得无论是CATIA或则其它软件，做曲面前规划曲面很重要，不能画到哪里是哪里，先构建基面和大过度面等，再添加细微特征和圆角特征等。

我们都会发现一般国外过来的数据都十分轨整，即使打上UV线，UV线的流向都十分整齐，而一般国外的数据都常常保留理论交线，这都是具备完整规划的曲面才可以做出类似“铁线尖角”模型通常经过规划的曲面模型，其曲面质量肯定是比较好。

最忌讳的是利用一个曲面来表现很多特征，无论是数据交换还是曲面质量一定会遇到不少麻烦。

实体也有同样的道理，先规划大轮廓，再做挖取部分，不要想起挖个洞就挖一个洞，想起补一块再补一块。

我从v4生成的exp文件中拖出了的model文件在五版本中打开时，如果是二维图，则提示说没有没有prj.model文件。

（我已经在option中设置了prj.model的路径了）请问如何在斯版本中声称这个文件？在五版本中读取四版本中的model文件有没有其它好办法？Top-Down 的思路已是欧美工程师的作业习惯了，除了设变的好处之外，当然在协同设计同步工程上也有相关的机制存在的，使用top-down 的观念从事设计工作最重视事前的规划，忌讳想到那里做到那里，而且要避免循环参考的问题，故有以下几点建议︰1.规划出共享的线架构及曲面的档案，即Layout Part, 将其放在总组立的第一个零件，所有零件皆以此为准2.先行插入共享零件及外购标准件，其定位点当然也是置于LayOut Part 中，以便日后进行设变单一化3.规划出几个大的次组件，在次组件中插入新零件进行零件的设计4.在零件数量渐渐变多时，仅量保持新零件参考旧零件的原则，避免循环参考的现象5.适当发布组件以利后续使用以上是一个大约的概念，若有不足请补充！以此法设计虽说是分成很多零件，但在零件设计时的方式也和在同一零件设计时方法一样并无特别的地方，当然要避免循环参考，若有发生这种现象时CATIA 会提醒你的，只要找出相关的父子关系就以解决这现象了ps : 在选项中的零件设计下要启动"与选取对象保持关联" 的选项！设计的基本方法即：自上而下或自下而上自上而下：1、可以构造骨架零件（在属性中将这个零件不显示在BOM 表中），然后将参考参数（点、线、面、控制变量等）发布（publish）;同时，我们在主骨架的控制下，可以构造子装配的骨架；在进行详细设计时，我们可以选择只关联发布元素，这样可以避免过多的参考，非关键元素在关联设计时生成的是只有子关系而没有父关系的元素，在进行大装配时，不致与造成系统崩溃；同时可以使用DMU的功能，在设计的同时检查设计的合理性，而这些检查皆可以挂在目录树中，使得我们可以重复的利用这些资源，我们只需要更新即可，而不必每次都从新选择等。

C a t i a--曲面设计第一章曲面设计概要1、曲面造型的数学概念：（1）、贝塞尔（Bezier）曲线与曲面：法国雷诺的Bezier在1962年提出的，是三次曲线的形成原理。

这是由四个位置矢量Q0、Q1、Q2、Q3定义的曲线。

通常将Q0，Q1，…，Qn组成的多边形折线称为Bezier控制多边形，多边形的第一条折线与最后一条折线代表曲线起点和终点的切线方向，其他折线用于定义曲线的阶次与形状。

（2）、B样条曲线与曲面：与Bezier曲线不同的是权函数不采用伯恩斯坦基函数，而采用B样条基函数。

（3）、非均匀有利B样条（NURBS）曲线与曲面：NURBS是Non-Uniform Rational B-Splines的缩写。

➢Non-Uniform（非统一）指一个控制顶点的影响力的范围能够改变。

当创建一个不规则曲面的时候，这一点非常有用。

同样，统一的曲线和曲面在透视投影下也不是无变化的，对于交互的3D建模来说，这是一个严重的缺陷。

➢Rational（有理）指每个NURBS物体都可以用数学表达式来定义。

➢B-Spline（B样条）指用路线来构建一条曲线，在一个或更多的点之间以内差值替换。

（4）NURBS曲面的特性及曲面连续性定义：NURBS曲面的特性：NURBS用数学方法来描述形体，采用解析几何图形，曲线或曲面上任何一点都有其对应的坐标（x,y,z），据有高度的精确性。

曲面G1与G2连续性定义：Gn表示两个几何对象间的实际连续程度。

●G0：两个对象相连或两个对象的位置是连续的。

●G1：两个对象光滑连接，一阶微分连续，或者是相切连续的。

●G2：两个对象光滑连接，二阶微分连续，或者两个对象的曲率是连续的。

●G3：两个对象光滑连接，三阶微分连续。

●Gn的连续性是独立于表示（参数化）的。

2、检查曲面光滑的方法：①、对构造的曲面进行渲染处理，可通过透视、透明度和多重光源等处理手段产生高清晰度的、逼真的彩色图像，再根据处理后的图像光亮度的分布规律来判断出曲面的光滑度。

用于DLP投影系统的自由曲面TIR准直透镜设计刘雁杰;惠彬;李景镇;丁金妃;朱天龙【摘要】In order to improve the collimation efficiency of illumination system of DLP projector and simplify the optical path, a free-form TIR lens is used as the collimating component. The coordinates of profile curve of the transmitting part and total reflecting part are calculated by Matlab according to the Snell's law and iterative method at first. Then the TIR lens model is established with Pro/E. The ideal point source and surface source are also used to do t he simulation. The view angle is collimated to±7°by the TIR lens. Finally, the suitable parameter of TIR lens is set according to DMD chip and LED source. The final uniformity of DLP illumination is about 90%, which can meet the related standard.%为了提高 DLP 投影照明系统中准直部分的准直度并简化准直光路,采用一种自由曲面的 TIR透镜作为 DLP 投影照明系统的准直器件.首先根据空间斯涅耳定律推导出反射曲面以及透射曲面母线上的点的坐标关系,并采用迭代的方法使用 Matlab 软件计算出母线上各个点的坐标并绘制出曲线图形,然后利用Pro/Engineer对TIR准直透镜进行建模得到TIR准直透镜的模型.分别用理想点光源和扩展光源进行模拟,经过TIR透镜准直后光束发散角在±7°以内,并根据选用的DMD芯片和LED光源选择合适的TIR透镜参数,建立DLP投影照明系统后进行模拟仿真,最终均匀度达到了90%,满足了投影照明系统的需求.【期刊名称】《红外技术》【年(卷),期】2015(037)007【总页数】6页(P582-587)【关键词】自由曲面;DLP;投影照明;准直透镜;光学设计【作者】刘雁杰;惠彬;李景镇;丁金妃;朱天龙【作者单位】深圳市微纳光子信息技术重点实验室,广东深圳 518060;深圳市微纳光子信息技术重点实验室,广东深圳 518060;深圳市微纳光子信息技术重点实验室,广东深圳 518060;深圳市微纳光子信息技术重点实验室,广东深圳 518060;深圳市微纳光子信息技术重点实验室,广东深圳 518060【正文语种】中文【中图分类】TN321.8现代投影技术按照投影显示芯片的不同可以分为LCD投影技术、LCOS投影技术和DLP投影技术。

几何迭代法及其应用综述摘要：儿何迭代法，又称渐进迭代逼近(progressive-iterative approximation, PI A),是一种具有明显几何意义的迭代方法.它通过不断调整曲线曲面的控制顶点，生成的极限曲线曲面插值(逼近)给定的数据点集.文中从理论和应用2个方面对几何迭代浓进行了综述.在理论方面，介绍了插值型几何迭代法的迭代格式、收敛性证明、局部性质、加速方法，以及逼近型几何迭代法的迭代格式和收敛性证明等.进而，展示了几何迭代法在几个方面的成功应用, 包括自适应数据拟合、大规模数据拟合、对称曲面拟合，以及插值给定位置、切矢量和曲率矢量的曲线迭代生成，有质量保证的四边网格和六面体网格生成，三变量B-spline体的生成等.关键词：渐进迭代逼近；几何迭代法；数据拟合；几何设计Survey on Geometric Iterative Methods with ApplicationsAbstract: Geometric iterative method, also called progressive-iterative approximation (PIA), is an iterative me- tliod with clear geometric meaning・ Just by adjusting the contiol points of cuives or suiiaces iteratively, tlie limit cuive or suiiace will mterpolate (approximate) the given data pomt set. Ill this paper, we mtroduce tlie geometric iterative method m two aspects, i.e., theory and application. In theory, we present the iterative formats of the mterpolatoiy and approxmiating geometiic iteration metliods, respectively, show thek convergence aiid local piopeity, and develop the acceleratmg teclnuques. Moieovei; some successfill applications of the geometiic itera・ tive metliods are demonstiated, mcludmg adaptive data fitting、large scale data fitting, syniinetiic suiiace fitting, generation of the cuive mteipolatmg given positions, tangent vectors, and cuivature vectors, generation of the quadiilateial and hexaliedral mesh with guaranteed quality, aiid generation of the tiivariate B-spline solid, etc.Key words: Piogressive-Iterative Approximation; Geometric Iterative Metliods; Data Fittmg; Geometric Design几何迭代法是一种具有明显几何意义的迭代方法.从一条初始混合曲线开始、通过迭代调整它的控制顶点，就可以使这条曲线插值或逼近给定的数据点列.由于几何迭代法的迭代过程具有明显的几何意义，在迭代的每一步，可以很容易地加入各种几何约束条件.使得几何迭代法生成的极限曲线曲面满足这些约束.由于几何迭代法的这一性质，近年来、它在几何设计及相关领域得到了成功地应用，包括自适应数据拟合，大规模数据拟合，对称曲面拟合、插值给定位置、切矢量和曲率第4期583矢屋的曲线迭代生成.有质虽保证的四边网格和六面体网格生成.三变B-splme体的生成等.几何迭代法垦始于1975年由齐东旭等学者提出的均匀3次B样条曲线的盈亏修正算法⑴，1979 年,de Boor也独立证明了这一算法的收敛性㈡.2004 年,Lm等证明了非均匀3次B样条曲线曲面的盈亏修正性质⑶；2006年，又证明了所有全正基混合曲线曲面都具有这一性质，并创造了英文术i吾progressive-iterative approximation(PIA:渐进迭代逼近)来描述这一方法同.在PIA算法中，每一个数据点对应的参数值在迭代中是固定不变的.2007 年，日本学者Maekawa等⑸将数据点的参数值取为每次迭代生成的拟合曲线曲面上最近点的参数值、并命名为geometric mterpolation(GI)［5'^.由于PIA和GI算法迭代步骤类似，都具有明显的几何意义，我们将这些具有明显几何意义的迭代法统称为几何迭代法.本文对几何迭代法的理论和应用进行了综述.1插值型几何迭代算法本节综述了几何设计中常用的几种曲线曲面的插值型几何迭代算法，包括全正基混合曲线曲面、NURBS 曲线曲面，三角Bernstem-Bezier(B-B)曲线曲面、以及细分曲线曲面等；同时还介绍了几何迭代法的加速技术和局部性质.1.1全正基混合曲线曲面的插值型几何迭代算法给定一个点列{0, ,=0, 1,…屮},其中每一个点0赋予一个参数值fi, /=0, 1, "，满足foWV”.以这个点列为初始控制点列.构造一条初始混合曲线P ⑼(/)= ”B (/);这里，为基另i i if=0函数，j=0, 1,…，假设第k次迭代后生成的第k 次曲线为/=0为进行第好1次迭代、首先计算差向量Aj 二QT然后，将其加到曲线砂匕的相应控制顶点上，即严=聊+妙，j=o,l,…，“；从而生成了第R+1次曲线严坊(/).这个过程迭代进行，产生了一个曲线序列{pQ(f)M = 0,l,2,・・・}・对于混合曲面(张虽积曲面)，也可以类似生成这样一个曲面序列［T.记山山伙) 伙)TA =［A L , A tl］⑴则式(1)矩阵形式［T为zfZ=(/_C)护；其中J为单位矩阵，弹0 （，0）C = |（o（“）恥0)Bn（，0 ） "1|5M） |13（，）L o 〃恥)1 nfB （/ ）nn」为基函数的配置矩阵.文献［3］中证明了当混合曲线曲面的基函数是非均勻3次B样条基函数时，这个曲线曲面序列收敛到插值于给定点列的曲线曲面、即伙)旣P (/.) = g./ = o,l，“；这称为混合曲线曲面的渐进迭代逼近(PIA)性质.进一步，文献［4］中证明了只要基函数是全正基函数, 这个曲线曲面序列就有渐进迭代逼近性质.由于Bernstein基函数和B样条基函数都是全正基函数, 因而Bezier曲线曲面、B样条曲线曲面都具有渐进迭代逼近性质•特别地，当混合曲线为周期均匀B样条曲线时，几何迭代的极限曲线表达式可以直接求出凹另外，文献［9］给出了渐进迭代的拟合误差估计公式.给定不同的拟合精度以及不同的初始数据参数化，利用拟合误差估计公式可以预估迭代次数.1.2 NURBS曲线曲面的插值型几何迭代算法我们首先构造NURBS曲线的几何迭代算法'NURBS曲面的几何迭代算法可以类似构造.NURBS曲线在射影空间中的齐次形式为f=0其中，Ri={wiPi, Wi)={wiXi, Wiyi, WiZi, Wi), j=o, 1，…,"； M7为权因子,?,=(.¥… >'j, 0)为欧氏空间的一个点，Bi⑴ 为Bernstein基函数或B样条基函数.它在3D欧氏空间中对应一条有理曲线Z也恥)P(f)=— ------- •flZ K)/=0584 第27卷给定齐次射影空间中一个点列{0= 30，i i i w,）=（“a，, WjZi，叫•）},构造一条初始曲线R⑼⑴二士呼乜⑴；i=0其中，K⑼=QM = o,i 在齐次形式下的几何迭代格式与第1.1节一样.这样产生了一个齐次形式表示的曲线序列{肿（°,=0 1 }.它对应着3D 欧氏空间中的一个有理曲线序列严（/）= _— / = 0,1,S 1 * J和一个权函数序列即），"0,1 }.可以证明上述2个序列都是收敛的，并且limP^（r）=e，/ = OJ 屮；f 盘Z = OJ 屮.13三角B・B曲面的插值型几何迭代算法这组点作为初始控制点，构造一张初始三角B-B 曲面T(0)(“』，w) = T{Q)B (U)B(V)B(W);2L ijk i j k其中,T®=Q r , W W1,H+U+W=1・了第力次三角B・B曲面(u)B(y)B (w)；S ijk i j k为生成第h+1次三角B-B曲面.计算(h) (h) // ijk= Qijk~T u.，v y Wk‘将其加到控制顶点巧贽上，得到第h+1次三角B-B 曲面的控制顶点这样，就生成了第h+1次三角B-B曲面穴3（“，V, W）.这个迭代过程产生了一个三角B-B曲面序列{T'\U^ V, w）, V, VtWl, Z/+ v + W=l}・当数据点对应的参数值取均匀参数时.即（i j k\（©,i”作）斗i,一厂」J +j + k ~n * 利用Bernstein算子忒疋於以及算子和矩阵的对应关系，Chen等证明了这个三角B-B曲面序列的收敛性卩气也就是hmT 叫W] =Q.力TX H n）秋在一般情况下，目前仅证明了4次和4次以下三角B-B 曲面序列的收敛性Z.1.4细分曲面的几何迭代算法本节中涉及的细分曲面为逼近型细分曲面. 具体为Catmull-Clark, Doo-Sabin 及Loop 细分曲面. 假设为一个细分曲面的控制网格顶点集合，其中，©为网格顶点.每一个网格顶点0在细分极體輛豔扁靂廳，缩如它可以表示为相2/.X = c lQi,l + 00,2 + + c k Qijc ■以给定的控制网格Q为初始控制网格旳={皆},算中⑼5 =0,可以生成一张初始细分曲面S • 假设第k次迭代后生成的第R次细分曲面GQ 的控制网格为p（k>={P k }p它的每一个网格顶点伙）⑹伙）P,在细分曲面S上的极限位置为P讦.构造差向屋£）=并将它加到第k次控制网格的顶点上，生成了第k+1次细分曲面外7的控制网格（好1丿=『（知叭（"1）=伙）伙）殆尸Pi ' Pi Pi +Ai 这样，就产生了一系列细分曲面序列{0气B0, 1,・・・}・当细分疊酸痂制咕器画皺翻髄轉?i它的控制网格中不存在度为3的顶点时，有（k）hmP,,8 =Qi・1.5插值型几何迭代算法的迭代速度和加速方法如第1.1节所述，当混合曲线曲面的基函数是全正基函数时，插值型几何迭代算法都收敛.由于B样条基函数和Bernstein基函数都是全正基函数，所以B样条曲线曲面和Bezier曲线曲面的插值型几何迭代格式都收敛.这两者之中、B样条曲线曲面的迭代速度更快[1S-19].插值型几何迭代法的加速是通过在差向虽dp前面乘以一个权因子3来实现的•这样.迭代格式变为P}H1）=砂"+血忡,/= 0,1, n.假设Zun为基函数配置矩阵的最小特征值、当2权因子取。