当前位置：文档之家 › 信息论基础与应用-李梅-第五章 无失真信源编码解析

信息论基础与应用-李梅-第五章 无失真信源编码解析

  • 格式：ppt
  • 大小：1.53 MB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

信息论基础与编码— 无失真信源编码ch05.article

信息论基础与编码— 无失真信源编码ch05.article

信息论基础与编码—无失真信源编码Contents1 无失真信源编码基本概念12 定长无失真信源编码23 渐进等同分割性54 定长无失真信源编码定理65 变长无失真编码85.1 Kraft 不等式 (8)5.2 唯一可译码判决准则. . . . . . . . . . . . . . . . . . . . . . . . . 96 变长无失真信源编码定理107 无失真信源编码技术117.1Huffman 编码 (12)7.2Shannon 编码 (12)7.3Shannon-Fano-Elias 编码 (12)7.4Fano 编码 (12)7.5Huffman 编码的几个问题 (13)7.6 算数编码. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147.7 游程编码. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157.8 通用编码. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157.9 几种编码方案的性能对比. . . . . . . . . . . . . . . . . . . . . . . 22 1 无失真信源编码基本概念•对于信源来说有两个基本问题：如何计算信源输出的信息量；如何有效地表示信源输出，即在不失真或允许一定失真的条件下，如何用尽可能少的符号来表示信源，以便提高信息传输的效率。

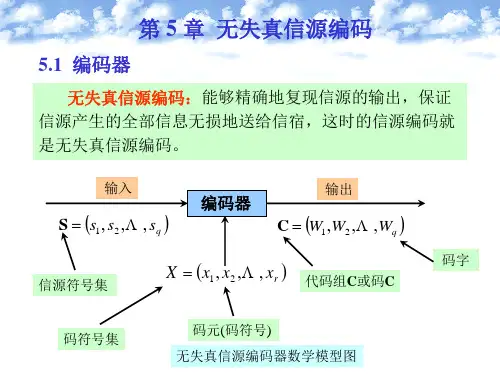
•编码实质上是对信源的原始符号按照一定的数学规则进行的一种变换。

1, . . . , W q }S : {s Array✻X : {x1, x2, . . . , x r }Figure 1: 信源编码器模型•将信源符号集合中的s i（或者长为N的信源符号序列）变换成由x j 组成的长度为l i 的一一对应的码符号序列W i。

信息论 基础理论与应用第三版(傅祖芸) 第5章 讲义

信息论 基础理论与应用第三版(傅祖芸) 第5章 讲义
l H ( S ) 2 N log r
则不可能实现无失真编码，当N趋向于无穷大时，译码错误 率接近于1。
•分析：定理中的条件式可写成
l log r NH (S )
左边: 长为 l 的码符号（码字）所能载荷的最大信息量； 右边: 长为N的信源符号序列平均携带的信息量。 因此，定理说明了：只要码字传输的最大信息量大于信源序 列携带的信息量，则可以实现无失真编码 。
第5章 无失真信源编码定理
5.1 编码器 5.2 等长码 5.4 等长信源编码定理 5.5 变长码 5.6 变长信源编码定理
引 言
信息通过信道传输到信宿的过程。要做到既不失真又快速地 通信，需要解决两个问题： 信源编码: 在不失真或允许一定失真条件下，提高信息传输率. 信道编码: 在信道受到干扰的情况下，增加信号的抗干扰能力，同时又 使得信息传输率最大.
信源 符号
码字
00: W1W1=B1
001:W1W2=B2 0001:W1W3=B3 0111:W1W4=B4
信源 符号
码字
010:W2W1=B5
信源 符号
码字
α1
α2 α3 α4
α5
： ： ：
：
： ： α16
：
： ：
111111:W4W4=B16
： ： ：
6、唯一可译码(单义可译码）
由码构成的任意一串有限长的码符号序列只能被唯一的 译成所对应的信源符号序列。 否则,就为非惟一可译码或非单义可译码。

最佳编码： 一般来说，抗干扰能与信息传输率二者相互矛盾。而编码 定理理论上证明，至少存在某种最佳的编码能够解决上述矛盾， 做到既可靠又有效地传输信息。 信源编码： 信源虽然多种多样，但无论是哪种类型的信源，信源符号 之间总存在相关性和分布的不均匀性，使得信源存在冗余度。 信源编码的目的就是要减少冗余，提高编码效率。

信息论课件第五章_无失真信源编码

信息论课件第五章_无失真信源编码

由此可见,当考虑信源符号之间依赖关系后,有 些信源符号序列不会出现,这样信源符号序列 个数会减少,再进行编码时,所需平均码长就可 以缩短. 英文 等长编码定理给出了信源进行等长编码所需 码长的理论极限值.
5.3 渐进等分割性和ε典型序列
渐进等分割性AEP是弱大数定理的直接推论 大数定理：若X1,X2,…，Xn是独立同分布的随机变 1 量，只要n足够大， ∑ X接近于数学期望E(X)。 n
α i (i = 1,..., q N ) 现在需要把这些长为N的信源符号序列
变换成长度为l的码符号序列 Wi = ( xi1 xi2 ...xil ), ( xi1 ,..., xil ∈ X )
根据前面的分析,若要求得编得的等长码是惟一 可译码则必须满足
qN ≤ rl (5.2)
此式表明,只有当l长的码符号序列数(rl)大于或 等于N次扩展信源的符号数(qN)时,才可能存在等 长非奇异码. 对式(5.2)两边取对数,则有
例如，表5.1中码１是惟一可译码，而码２是 非惟一可译码。 因为对于码２，其有限长的码符号序列能译 成不同的信源符号序列。如：0010,可译成 s1s2s1或s3s1,显然不是惟一的。 下面，我们分别讨论等长码和变长码的最佳 编码问题，也就是是否存在一种惟一可译编 码方法，使平均每个信源符号所需的码符号 最短。也就是无失真信源压缩的极限值。
sik ∈ S ( k = 1, 2,..., N ) xik ∈ X ( k = 1, 2,..., li )
这种码符号序列Wi，称为码字。长度li称为码字长 度或简称码长。所有这些码字的集合C称为码（或 称码书）此码为r元码或称r进制码。
编码就是从信源符号到码符号的一种映射 若要实现无失真编码，必须这种映射是一一 对应的、可逆的。

信息论基础第5章无失真信源编码

信息论基础第5章无失真信源编码
进行霍夫曼编码时，应把合并后的概率总是放在 其他相同概率的信源符号之上，以得到码长方差最小 的码。
r 元霍夫曼编码步骤：
1) 验证所给 q 是否满足 q (r 1) r ，若不满足该式，
可以人为地增加 t 个概率为零的符号，满足式
n (r 1) r ，以使最后一步有 r 个信源符号；
2) 取概率最小的 r 个符号合并成一个新符号，并分别用 0， 1，…，(r 1) 给各分支赋值，把这些符号的概率相加作为该新 符号的概率；
上述不等式只是即时码存在的充要条件，而不能作为判别的依据。
需要注意的是，克拉夫特不等式是即时码存在的充要条件，而 不能作为判别的依据。后来麦克米伦（B. McMillan）证明唯一可译 码也满足克拉夫特不等式。这说明在码长选择的条件上，即时码与 唯一可译码是一致的。
【例】 对于二元码，即 r 2 ，如果 q 4 ， L1 2 ， L2 2 ，
原始信源普遍存在剩余度，香农信息论认为信源的剩余度主 要来自两个方面：一是信源符号间的相关性，二是信源符号概率 分布的不均匀性。为了去除信源剩余度，提高信源的信息传输率， 必须对信源进行压缩编码。
目前去除信源符号间相关性的主要方法是预测编码和变换编 码，而去除信源符号概率分布不均匀性的主要方法是统计编码。
《信息论基础》
第5章 无失真信源编码
第 2 章已经讨论了离散信源的信息度量—信源熵， 本章将讨论信源的另一个重要问题：如何对信源的输出 进行适当的编码，才能用尽可能少的码元来表示信源信 息，做到以最大的信息传输率无差错地传输信息呢？即 无失真信源编码，它解决的是通信的有效性问题。
本章将首先介绍信源编码器；然后从理论上阐述无 失真信源编码定理，得出“平均码长的理论极限值就是

信息论与编码chapter5

信息论与编码chapter5

渐进均分特性
典型序列的概率估计
设 x G 1 ( 满 足 公 式 5 .3 )
log p ( x ) N H (X )
N [ H ( X ) ] log p ( x ) N [ H ( X ) ]
设取2为底 2 N [ H ( X ) ] p ( x ) 2 N [ H ( X ) ]
（适用于离散信源的编码）
限失真信源编码： 信源符号不能通过编码序列无 差错地恢复。
（可以把差错限制在某一个限度内）
信源编码的目的：提高传输有效性，即用尽可能短 的码符号序列来代表信源符号。
§5.1 信源编码的相关概念
本节主要内容
一、信源编码器 二、码的分类 三、分组码
§5.1.1 信源编码器
将信源符号集中的每一个符号固定映 射成一个码字的码 分组码单符号信源编码器
第五章 无失真信源编码
主要内容
本章主要介绍无失真信源编码定理与一 些重要的无失真信源编码方法
一、概述 二、定长码 三、变长码
四、哈夫曼编码
信源编码：将信源符号序列按一定的数学规律映射 成由码符号组成的码序列的过程。 信源译码： 根据码序列恢复信源序列的过程。 无失真信源编码： 即信源符号可以通过编码序列 无差错地恢复。
若不满足上式 =
H (X
N
l N
l l
log r H ( X )
;Y )
N
l
) H (X
N
/ Y ) H (Y ) lH (Y ) l log r
H (X
) NH ( X )
H (X
N
/ Y ) NH ( X ) l log r 0

第5章_无失真信源编码

第5章_无失真信源编码
l •定理5.3的条件式也可写成： N log r H (S ) l 令：R ' log r 称之为编码信息率。可见，编码信息 N
率大于信源的熵，才能实现无失真编码。
H (S ) H (S ) l R' log r N
为了衡量编码效果，引进
称为编码效率。
H (S )
15
H (S ) H (S ) 最佳编码效率为： ' R H (S )
信源编码理论是信息论的一个重要分支，其理论基础是信源编码的两个定理。
限失真信源编码定理：香农第三定理
是连续信源/模拟信号编码的基础。
信源编码的分类：离散信源编码、连续信源编码和相关信源编码三类。
离散信源编码：独立信源编码，可做到无失真编码；
连续信源编码：独立信源编码，只能做到限失真信源编码； 相关信源编码：非独立信源编码。
q N r l ， 两边取对数得： l log q
l N
N
log r
表示平均每个信源符号所需的码符号个数。
DUT
信息论基础
9
5.2 等长码
例：对英文电报得32个符号进行二元编码，根据上述关系：
log 32 l 5 log 2
我们继续讨论上面得例子，我们已经知道英文的极限 熵是1.4bit,远小于5bit，也就是说，5个二元码符号只携 带1.4bit的信息量，实际上，5个二元符号最多可以携带 5bit信息量。我们可以做到让平均码长缩短，提高信息传 输率
8、唯一可译码：
若码的任意一串有限长的码符号序列只能被唯一的译成 所对应的信源符号序列，则称此码为唯一可译码。
DUT
信息论基础
8
5.2 等长码
若对信源进行等长编码，则必须满足

信息论与编码 限失真信源编码

信息论与编码 限失真信源编码

第一节 失真测度
1、失真度
信源 信源 编码 信道 编码 广义无扰信道
信道
干扰
信道 译码
信源 译码
信宿
失真范围: 由于只涉及信源编码问题, 所以可以将信 道编码和信道译码看成是信道的一部分. 这样信宿 收到消息的失真(或误差)只是由信源编码带来的.
第一节 失真测度

试验信道: 由于是失真编码, 所以信道不是一一
前 言

失真传输的研究方向:

在允许一定程度失真的条件下, 能把信源信息压 缩到什么程度, 即最少需要多少比特数才能描述
信源;

也就是说, 在允许一定程度失真的条件下, 如何
能快速地传输信息, 这是本章要讨论的问题。
前 言

这个问题在香农1948年最初发表的经典论文中已 经有所体现, 但直到1959年香农又发表了“保真
条件下, 如何能快速的传输信息, 这就是本章所要讨
论的问题. 本章所讨论的内容是量化、数模转换、频带压 缩和数据压缩的理论基础.
前 言
本章主要介绍信息率失真理论的基本内容, 侧重 讨论离散无记忆信源. 首先给出信源的失真度和信息率失真函数的定义
与性质, 然后讨论离散信源的信息率失真函数计算.
在这个基础上论述保真度准则下的信源编码定理.
前 言

失真传输的可能性:

传送图像时, 也并不是需要全部精确地把图像传送到
观察者. 只需将电视信号每一像素的黑白灰度级分成
256级, 屏幕上的画面就已足够清晰悦目.

对于静止图像或活动图像, 从空间频域来看, 每一帧一 般只含有大量的低频域分量, 高频域分量很少. 若将高 频分量丢弃, 只传输或存储低频分量, 数据率便大大减 少, 而图像质量仍能令人满意. 这是因为人眼有一定的 主观视觉特征, 允许传送图像时有一定的误差存在.

(信息论)第5章无失真信源编码

(信息论)第5章无失真信源编码
这就是说，每个英文电报符号至少要用5位二元符号进行 编码才能得到唯一可译码。 12
定长编码定理
定长信源编码定理讨论了编码的有关参数对译 码差错的限制关系
sq p s q
定理 5.3.1 设离散无记忆信源
S s1 P p s 1 p s 2 s2
的熵为H S ，其 N 次扩展信源为
S N 1 p 1 P
2 q p 2 p q

N N

现在用码符号集 X x1 , x2 ,, xr 对N次扩展信源 S N 进行长度为 l 的定长编码，对于 0, 0 ，只要满足
l H S N log r
则当 N 足够大时，译码错误概率为任意小，几乎可以实 现无失真编码。 反之，若满足
l H S 2 N log r
则不可能实现无失真编码。而当N足够大时，译码错误概 14 率近似等于1。

以上的定理5.3.1 和定理5.3.2实际上说明的是一个 问题，虽然该定理是在平稳无记忆离散信源的条件下 证明的，但它也同样适合于平稳有记忆信源，只要要 2 求有记忆信源的极限熵 H S 和极限方差 存在 即可。对于平稳有记忆信源，式(5.6)和式(5.7 ) 中 H S 应该为极限熵 H S 。
变长码(可变长度码)
2
奇异码：若码中所有码字都不相同，则称此码为非
奇异码。反之，称为奇异码。
同价码：每个码符号所占的传输时间都相同的码。定
长码中每个码字的传输时间相同。而变长码中的每个码 字的传输时间不一定相等。
表 5.1
信源符号si
信源符号出现概率 si p

2015秋.信息论.第5章限失真信源编码

2015秋.信息论.第5章限失真信源编码

r r 1 N 1 d N ( x , y ) d ( xi , yi ) d ( x1 , y1 ) d ( x2 , y2 ) d ( x3 , y3 ) N i 1 3
1 1 d3 000,000 d 0,0 d 0,0 d 0,0 0 0 0 0 3 3 1 1 1 d3 000,001 d 0,0 d 0,0 d 0,1 0 0 1 3 3 3
常见失真函数： 1. 汉明失真： 0， if x y, d ( x, y ) 1， if x y.
2. 平方失真：
2 d ( x, y ) （y x） .
3. 绝对失真： d (x, y ) y x
图像处理中，常用平方误差和绝对误差度量失真
9
若源符号集A包含r个符号，码符号集B包含s个符号，
5.1.2 平均失真
失真函数的数学期望称为平均失真。
D E[d ]
i
p( x y
i i j j
j
)d ( xi , y j )
p ( x ) p ( y
i j
| xi )d ( xi , y j ).
单个符号的 失真函数
信源特性
试验信 道特性
矢量平均失真： DN 1 E[ d N ] N 1 E[d ( xi , yi )] N i 1
13
例7.1.2 假定离散矢量信源N=3，输出矢量序列为X=X1X2X3， 其中Xi的取值为{0,1}；经信道传输后的输出为Y=Y1Y2Y3， 其中Yi的取值为{0,1}。定义失真函数
d 0， 0 d 11 ， 0 d 0， 1 d 1， 0 1

信息理论与编码第5章

信息理论与编码第5章

2.唯一可译性 定义2 若一个分组码的任意一串有限长码序列，只能唯一
地分割一个个的码字，则称为唯一可译码。 唯一可译码又称为单义码。 例 分组码为: s1→1 s2→10 s3→11 s1s1 →11 ，s3→11， s1s1 与 s3 不是一一对应的。
s2 s3 s1… 10 111 …. s2 s1 s1 s1 … s2 s1 s3 …
5.1 信源编码器
信源
编码器
信道
码表
1. 信源的符号集和符号序列
1°信源符号集
信源发出的符号消息的集合，记为S；设 S 有q个符号：
S 2°信源符号序列:Βιβλιοθήκη ={s1,
s2
,
…
,
sq
}
由信源符号集合 S 中符号的N 次扩展组成长度为N 的
符号序列，符号序列的集合记为 S N ；
N — 信源符号序列长；
非唯一可译码对有限长码流，不能唯一地分割一个个 的码字。唯一可译码在传输过程中不需要同步码。
非奇异定长码是唯一可译码
3.即时性 定义 在分组码形成码序列中，一个完整的码字接收到后，
无需等到接收下一个码字，就能立即译码，称为即 时码。
即时码又称为非延长码、异前缀码或逗点码。
异前缀码(即时码)指的是码集任何一个码不能是其他 码的前缀。
信息论与编码
Information Theory & Coding 第5章 无失真信源编码
信源编码一直是信息论研究的一个重要方向。信源编 码是通过压缩编码来去掉信号源中的冗余成分，提高信息 传输的有效性。
本章的重点
1.信源编码的概念； 2.变长码的分类与主要编码方法； 3.惟一可译码的判别准则； 4. Huffman编码

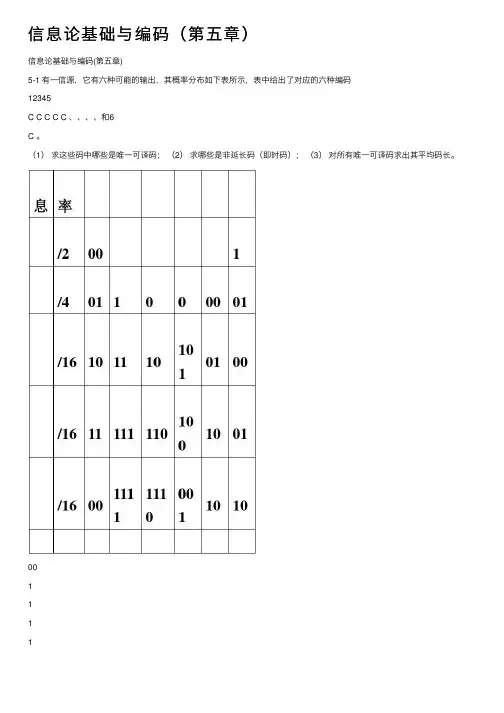
信息论基础与编码（第五章）

信息论基础与编码（第五章）

信息论基础与编码（第五章）信息论基础与编码(第五章)5-1 有⼀信源，它有六种可能的输出，其概率分布如下表所⽰，表中给出了对应的六种编码12345C C C C C 、、、、和6C 。

（1）求这些码中哪些是唯⼀可译码；（2）求哪些是⾮延长码（即时码）；（3）对所有唯⼀可译码求出其平均码长。

001111解：（1）1,2,3,6是唯⼀可译码； (2)1,3,6是即时码。

5-2证明若存在⼀个码长为12,,,ql l l 的唯⼀可译码，则⼀定存在具有相同码长的即时码。

证明：由定理可知若存在⼀个码长为的唯⼀可译码，则必定满⾜kraft 不等式1。

由定理4可知若码长满⾜kraft 不等式，则⼀定存在这样码长的即时码。

所以若存在码长的唯⼀可译码，则⼀定存在具有相同码长P （y=0）的即时码。

5-3设信源126126()s s s S p p p P s=?，611ii p==∑。

将此信源编码成为r 元唯⼀可译变长码（即码符号集12{,,,}r X x x x =），其对应的码长为（126,,,l l l ）=（1，1，2，3，2，3），求r 值的最⼩下限。

解：要将此信源编码成为 r 元唯⼀可译变长码，其码字对应的码长（l 1 ,l 2 ,l 3, l 4,l 5, l 6）=(1,1,2,3,2,3) 必须满⾜克拉夫特不等式，即LqL L ,,2,1Λ∑=-qi l ir1≤4?LqL L ,,2,1Λ132321161≤+++++=------=-∑r r r r r r ri li所以要满⾜ 122232≤++rr r ，其中 r 是⼤于或等于1的正整数。

可见，当r=1时，不能满⾜Kraft 不等式。

当r=2, 1824222>++，不能满⾜Kraft 。

当r=3, 127262729232<=++，满⾜Kraft 。

所以，求得r 的最⼤值下限值等于3。

5-4设某城市有805门公务电话和60000门居民电话。

信息论与编码5----无失真信源编码1

信息论与编码5----无失真信源编码1

∑2
i =1
4
li
=2

+2
2
+2
2
+2
3
9 = >1 8
因此不存在满足这种码长的唯一可译码.可以用 树码进行检查.
信息论与编码-无失真信源编码
唯一可译码的判断法(变长): 将码C中所有可能的尾随后缀组成一个集合F,当 且仅当集合F中没有包含任一码字,则可判断此 码C为唯一可译码. 集合F的构成方法: 首先,观察码C中最短的码字是否是其它码字的 前缀,若是,将其所有可能的尾随后缀排列出. 而这些尾随后缀又有可能是某些码字的前缀, 再将这些尾随后缀产生的新的尾随后缀列出,
信息论与编码-无失真信源编码
与码字是一一对应的,并求由码字组成的符号序 列的逆变换也是唯一的(唯一可译码). 定长编码定理: 定长编码定理 由L个符号组成的,每个符号熵为 HL(X) 的无记忆 平稳信源符号序列 X 1 X 2 L X L ,可用 K L 个符号 Y1Y 2 L Y K L (每个符号有m中可能值)进行定长 变码.对任意 ε > 0, δ > 0 ,只要
信息论与编码-无失真信源编码
P σ 2 ( X ) 和 ε 2 均为定值时,只要L足够大, ε 可 当
一小于任一整数δ ,即
σ 2(X ) ≤δ 2 Lε
此时要求:
σ 2(X ) L≥ ε 2δ
信息论与编码-无失真信源编码
只要 δ 足够小,就可以几乎无差错地译码,当然 代价是L变得更大. 令 KL
KL log m ≥ H L ( X ) + ε L
信息论与编码-无失真信源编码
则当L足够大时,必可使译码差错小于δ ;反之, 当
KL log m ≤ H L ( X ) 2ε L

信息论基础与应用-李梅-第五章 无失真信源编码资料

信息论基础与应用-李梅-第五章 无失真信源编码资料
p(s2)=1/4 p(s3)=1/8 p(s4)=1/8
00
01 10 11
0
01 001 111
第五章：无失真信源编码
一、信源编码的相关概念
3. N次扩展码
S s1 , s2 ,, sq


siBiblioteka C {w1 , w2 ,
, wq }
wi
S s1 , s2 ,
N

, sqN

s jN
计匹配编码，根据信源的不同概率分布而选用与之相 匹配的码。
第五章：无失真信源编码
一、信源编码的相关概念
1. 信源编码概述（续2）

信源的统计剩余度主要决定于以下两个因素 ： 1）无记忆信源中，符号概率分布的非均匀性； 2）有记忆信源中，符号间的相关性及符号概率分布 的非均匀性。

怎样压缩信源的冗余度？
C N {w1 , w 2 ,, w q N }
w j w j1 w j2 w jN
s j s j1 s j2
j 1,2,, q N
j1 , j2 ,, jN 1,2,, q
第五章：无失真信源编码
一、信源编码的相关概念
3. N次扩展码（续1）
二次扩展信源符号 s j ( j 1, 2,...,16)
若一个码中所有码字的码长都相等，则称为定长码；
否则为变长码。
第五章：无失真信源编码
一、信源编码的相关概念
5. 奇异性
若一个码中所有码字互不相同，则称为非奇异码； 否则为奇异码。
信源符号si 码1 码2
s1 s2 s3 s4
0 11 00 11
0 10 00 01
第五章：无失真信源编码

第五章 无失真信源编码定理

第五章 无失真信源编码定理
则不可能实现无失真编码。
第三节 等长信源编码定理
•定理5.3的条件式可写为：
长为l 的码符号所能 载荷的最大信息量 长为N的序列平均携带的信息量
l log r > NH ( S )
只要码字传输的信息量大于信源序列携带的 信息量，总可以实现无失真编码。 l •定理5.3的条件式也可写成： log r H ( S ) e N
i
N
1
2
N
是一一对应的：
i Bi (Wi1 ,Wi2 , ,WiN ), i S ,Wil C
N
4）惟一可译码 若任意一串有限长的码符号序列只能被惟 一地译成所对应的信源符号序列，则此码称 为惟一可译码（或称单义可译码）；否则就 称为非惟一可译码或非单义可译码。
例：对于二元码 C1 {1, 01, 00} ，当任意给定一串 码字序列，例如“10001101”，只可唯一地划 分为1,00,01,1,01，因此是惟一可译码；而对 另一个二元码 C 2 {0,10, 01} ，当码字序列为 “01001”时，可划分为0,10,01或01,0,01，所 以是非惟一可译的。
P(G eN )
-
(2) 若 i (si1, s i2 ,...,s iN ) GeN，则 2 - N [ H ( s )e ] < P( i ) < 2 - N [ H ( s ) -e ] (3) || GeN || 表示e典型序列集中 e典型序列的个数，则 (1 - )2 N [ H ( s )-e ] <|| GeN ||< 2 N [ H ( s ) e ]
1 N - log P ( si ) 以概率收敛于均值 H ( s ) 熵定义 N i 1 1 N 1 即 - log P ( s i ) - log[ P ( s i ) P ( s 2 ) L P ( s N )] N次扩展信源 N i 1 N 1 - log P ( si s 2 L s N ) H ( S ) 以概率收敛 N 因为 i1 ( si1 si 2 L s i N ) S1 S 2 L S N , (i 1, 2 , L , q N i1 , i2 , L , i N 1, 2 , L , q )

信息论与编码[第五章无失真信源编码定理与编码]山东大学期末考试知识点复习

信息论与编码[第五章无失真信源编码定理与编码]山东大学期末考试知识点复习

第五章无失真信源编码定理与编码5．1．1 信源编码和码的类型1．信源编码2．码的类型若码符号集中符号数r=2称为二元码，r=3称为三元码，……，r元码。

若分组码中所有码字的码长都相同则称为等长码，否则称为变长码。

若分组码中所有码字都不相同则称为非奇异码，否则称为奇异码。

若每个码符号x i∈X的传输时间都相同则称为同价码，否则称为非同价码。

若分组码的任意一串有限长的码符号只能被唯一地译成所对应的信源符号序列则称为唯一可译码，否则称为非唯一可译码。

若分组码中,没有任何完整的码字是其他码字的前缀，则称为即时码（又称非延长码或前缀条件码），否则称为延长码。

本章主要研究的是同价唯一可译码.5．1．2 即时码及其树图构造法即时码（非延长码或前缀条件码)是唯一可译码的一类子码。

即时码可用树图法来构造。

构造的要点是:（1）最上端为树根A，从根出发向下伸出树枝，树枝总数等于r，树枝的尽头为节点。

（2）从每个节点再伸出r枝树枝，当某节点被安排为码字后,就不再伸枝，这节点为终端节点。

一直继续进行，直至都不能伸枝为止。

(3）每个节点所伸出的树枝标上码符号，从根出发到终端节点所走路径对应的码符号序列则为终端节点的码字。

即时码可用树图法来进行编码和译码。

从树图可知，即时码可以即时进行译码。

当码字长度给定，即时码不是唯一的。

可以认为等长唯一可译码是即时码的一类子码。

5．1．3 唯一可译码存在的充要条件（1)对含有q个信源符号的信源用含r个符号的码符号集进行编码,各码字的码长为l1，l2,…,l q的唯一可译码存在的充要条件是,满足Kraft不等式5．1．4 唯一可译码的判断法唯一可译码的判断步骤:首先，观察是否是非奇异码.若是奇异码则一定不是唯一可译码。

其次，计算是否满足Kraft不等式。

若不满足一定不是唯一可译码。

再次，将码画成一棵树图，观察是否满足即时码的树图的构造,若满足则是唯一可译码。

或用Sardinas和Patterson设计的判断方法：计算出分组码中所有可能的尾随后缀集合F，观察F中有没有包含任一码字，若无则为唯一可译码;若有则一定不是唯一可译码.上述判断步骤中Sardinas和Patterson设计的判断方法是能确切地判断出是否是唯一可译码的方法,所以可以跳过前三个步骤直接采用该判断法。

第五章：无失真编码1

第五章：无失真编码1

实际信源举例

对于数字型图像信号，可以采用马氏链模型
1 2 X x 2 N 1

1
2 N 1
1 1
而
为相邻像素之间的相关系数。实际信源举例2）语音信源 可以近似用一个一维随机过程U(ω, t)表示。 严格的讲，它是一个非平稳过程，但是对于 短时段(5-50ms)可认为是平稳的，且某些是 随机噪声（清辅音）而某些时段则呈现周期 性特征（浊音），还有一些短时段是二者的 混合。

无记忆信源


在某些简单的离散平稳信源情况下，信源先后发出 的一个个符号彼此是统计独立的。也就是说信源输 出的随机矢量 X=(X１X２…XＮ）中，各随机变量 Xi (i=1,2,…N) 之间是无依赖的、统计独立的，则 N 维 随机矢量的联合概率分布满足 P(X)=P １（Ｘ １） P２ （Ｘ２）…PＮ（ＸＮ） 我们称由信源空间［X，P(x)］描述的信源X为离散 无记忆信源。这信源在不同时刻发出的符号之间是 无依赖的，彼此统计独立的。
可能取值。
离散序列信源

例：最简单 L=3 的三位 PCM 信源：这时 L=3, n=2, 即i={0,1}，则有：
U 3 U 000, U 001,, U 111 3 2 3 p(u ) p , p p , p 0 0 1 1

离散序列信源总结
离散无记忆信源 离散序列信源 离散有记忆信源
一般无记忆 平稳无记忆 平稳序列信源 时齐马氏链信源
随机波形信源


更一般地说，实际信源输出的消息常常是时间和取值都是连续的。例如，语音 X(t)、热噪声信号n(t)、电视图像信号X(x0,y0,t)等时间连续函数。同时， 在某一固定时间t０，它们的可能取值又是连续的和随机的。对于这种信源输出 的消息，可用随机过程来描述。称这类信源为随机波形信源。 分析一般随机波形信源比较复杂和困难。常见的随机波形信源输出的消息是时 间上或频率上为有限的随机过程。根据取样定理，只要是时间上或频率上受限 的随机过程，都可以把随机过程用一系列时间(或频率)域上离散的取样值来表 示，而每个取样值都是连续型随机变量。这样，就可把随机过程转换成时间(或 频率)上离散的随机序列来处理。甚至在某种条件下可以转换成随机变量间统计 独立的随机序列。如果随机过程是平稳的随机过程，时间离散化后可转换成平 稳的随机序列。这样，随机波形信源可以转换成连续平稳信源来处理。若再对 每个取样值(连续型的)经过分层(量化)，就可将连续的取值转换成有限的或可数

信息论第5章 无失真信源编码

信息论第5章 无失真信源编码
若码长l1, l2, …, lq 不满足Kraft不等式à 不是惟一可译码；反之， l1, l2, …, lq 满 足Kraft不等式的码，不一定是惟一可译码。 结论：不能用克拉夫特不等式，只能根据定义 判断码C是否是惟一可译码。 判别依据：非惟一可译变长码 有限长的码 符号序列能译成两种不同的码字序列。
66
香农第一定理的物理意义
无失真信源编码的实质：对离散信源进行变换 变换后信源符号(信道的输入信源)尽可能为等概 率分布 新信源符号平均所含的信息量达到最大 à 使信道的信息传输率R达到信道容量C，实现 信源与信道理想的统计匹配。 无失真信源编码定理通常又称为无噪信道编码定 理。表述为：若信道的信息传输率R不大于信道 容量C，总能对信源的输出进行适当的编码，使 得在无噪无损信道上能无差错地以最大信息传输 率C传输信息，但要使信道的信息传输率R大于C 而无差错地传输信息则是不可能的。
62
63
64
65
定理4.8（香农信息论的主要定理之一）的结论：
要做到无失真的信源编码，编码每个信源符号平均所 需最少的r元码元数为信源的熵Hr(S) 。即Hr(S) 是无 失真信源压缩的极限值。 若编码的平均码长小于信源的熵值Hr(S) ，则惟一可 译码不存在，在译码或反变换时必然要带来失真或差 错。 通过对扩展信源进行变长编码，当N ∞时，平均码长 Hr(S) 。
4
几个术语： 信源符号：信源输入S={s1,s2,…,sq} 码符号 (码元)：X={x1,x2,…,xr} 码字Wi： 由xj (j=1,2,…,r)组成的长度为 li 的序列，Wi与si一一对应。 码字长度 (码长)： Wi的长度li 码 (码书)：码字Wi的集合 C={W1,W2,…,Wq} 编码器：将信源符号si变换成Wi的设备
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
s1 s1s1 s 2 s1s2 s3 s1s3 s16 s4 s4
二次扩展码码字 w j ( j 1, 2,...,16)
w1 w1w1 00 w 2 w1w2 001 w3 w1w3 0001 w16 w4 w4 111111
第五章：无失真信源编码
一、信源编码的相关概念
4. 关于编码的一些术语

编码器输出的码符号序列 wi称为码字；长度 li 称为码 字长度，简称码长；全体码字的集合C称为码。 若码符号集合为X={0,1}，则所得的码字都是二元序 列，称为二元码。

将信源符号集中的每个信源符号
si 固定的映射成某
一个码字 wi ，这样的码称为分组码。
码字与信源符号一一对应
2) 不同的信源符号序列对应不同的码字序列
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续2）
例1：
1) 奇异码
s1 s2 s3 s4
0 11 00 Байду номын сангаас1
译码 11
s2 s4
奇异码一定不是唯一可译码
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续3）
译码 0 0 0 1 1 0 1 1
s1s2 s3 s4
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续5）
4)
唯一可译码 1 1 0 1 0 0 1 0 0 0 0
s1 s2
1 10
1 0
1
s2 / s3 ?
s3 100 s4 1000

为非即时码
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性
若任意一串有限长的码符号序列只能被唯一地译为 对应的信源符号序列，则称此码为唯一可译码。

信源符号si s1 s2 s3 s4
码1 0 11 00 11
码2 0 10 00 01
码3 0 10 110 111
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续1）

唯一可译码应当满足的条件 1) wi (i 1, 2,..., q) si (i 1, 2,..., q)
第五章：无失真信源编码
一、信源编码的相关概念
2. 信源编码器模型（续2）
例: 5.1
S s1 P p( s ) 1
p(si)
s2 p( s2 )
码1
s3 p ( s3 )
s4 p ( s4 )
码2
信源符号si
s1
s2 s3 s4
p(s1)=1/2
1) 去除码符号间的相关性。
2) 使码符号等概分布。
第五章：无失真信源编码
一、信源编码的相关概念
2. 信源编码器模型
信源编码：将信源符号序列按一定的数学规律映射成 码符号序列的过程。

S
信源
X 编码器
信道
Y 译码器
S’
信宿
S s1 , s2 ,, sq


X {x1 , x2 , , xr }
第五章：无失真信源编码
一、信源编码的相关概念 二、定长码及定长信源编码定理
三、变长码及变长信源编码定理 四、变长码的编码方法
五、实用的无失真信源编码方法
第五章：无失真信源编码
一、信源编码的相关概念
1. 信源编码概述

信源编码的作用：
使信源适合于信道的传输，用信道能传输的符号来代
表信源发出的消息； 在不失真或允许一定失真的条件下，用尽可能少的符 号来传递信源消息，提高信息传输率。
2) 非奇异码
s1 0 s2 10 s3 s4 00 01
译码 0 10 00 01 0 译码
s1s2 s3 s4 s1
01 00
00 10
s4 s3 s3 s2
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续4）
3)
等长码

非奇异码

唯一可译码
s1 s2
00 01
s3 10 s4 11
p(s2)=1/4 p(s3)=1/8 p(s4)=1/8
00
01 10 11
0
01 001 111
第五章：无失真信源编码
一、信源编码的相关概念
3. N次扩展码
S s1 , s2 ,, sq


si
C {w1 , w2 ,
, wq }
wi
S s1 , s2 ,
N

, sqN

s jN
若一个码中所有码字的码长都相等，则称为定长码；
否则为变长码。
第五章：无失真信源编码
一、信源编码的相关概念
5. 奇异性
若一个码中所有码字互不相同，则称为非奇异码； 否则为奇异码。
信源符号si 码1 码2
s1 s2 s3 s4
0 11 00 11
0 10 00 01
第五章：无失真信源编码
一、信源编码的相关概念
图1 信源编码器模型
第五章：无失真信源编码
一、信源编码的相关概念
2. 信源编码器模型（续1）
S s1 , s2 ,, sq


编码器
C {w1 , w2 ,
, wq }
X : {x1 , x2 ,..., xr }
码字

wi xi1 xi2
xil
i
将信源符号集中的符号 s（或者长为 N的信源符号序 i 列）映射成由码符号 xi 组成的长度为 li 的一一对应的码 符号序列 wi 。
以提高通信有效性为目的。通常通过压缩信源的冗余 度来实现。采用的一般方法是压缩每个信源符号的平 均码长。

第五章：无失真信源编码
一、信源编码的相关概念
1. 信源编码概述（续1）
信源编码理论是信息论的一个重要分支，其理论基础 是信源编码的两个定理：

无失真信源编码定理 限失真信源编码定理

本章主要介绍无失真信源编码，它实质上是一种统
C N {w1 , w 2 ,, w q N }
w j w j1 w j2 w jN
s j s j1 s j2
j 1,2,, q N
j1 , j2 ,, jN 1,2,, q
第五章：无失真信源编码
一、信源编码的相关概念
3. N次扩展码（续1）
二次扩展信源符号 s j ( j 1, 2,...,16)
6. 唯一可译性（续6）
5) 唯一可译码
s1 s2 s3 s4
计匹配编码，根据信源的不同概率分布而选用与之相 匹配的码。
第五章：无失真信源编码
一、信源编码的相关概念
1. 信源编码概述（续2）

信源的统计剩余度主要决定于以下两个因素 ： 1）无记忆信源中，符号概率分布的非均匀性； 2）有记忆信源中，符号间的相关性及符号概率分布 的非均匀性。

怎样压缩信源的冗余度？