信息论与编码第5章
- 格式:doc
- 大小:475.00 KB
- 文档页数:32


设信源1234567()0.20.190.180.170.150.10.01X a a a a a a a p X ⎡⎤⎧⎫=⎨⎬⎢⎥⎣⎦⎩⎭(1) 求信源熵H(X); (2) 编二进制香农码; (3) 计算平均码长和编码效率.解: (1)721222222()()log ()0.2log 0.20.19log 0.190.18log 0.180.17log 0.170.15log 0.150.1log 0.10.01log 0.012.609/i i i H X p a p a bit symbol==-=-⨯-⨯-⨯-⨯-⨯-⨯-⨯=∑(2)(3)71()0.230.1930.1830.1730.1530.140.0173.141()()/ 2.609 3.14183.1%i i i K k p x H X H X K Rη===⨯+⨯+⨯+⨯+⨯+⨯+⨯====÷=∑对习题的信源编二进制费诺码,计算编码效率.解:a i p(a i )编码码字k ia10002 a2100103 a310113 a410102 a5101103 a61011104 a7111114对信源编二进制和三进制哈夫曼码,计算各自的平均码长和编码效率.解:二进制哈夫曼码:x i p(x i)编码码字k i s61s50s41s30s21x10102 x21112 x300003x410013 x500103 s11x6001104 x7101114三进制哈夫曼码:x i p(x i)编码码字k i s31s20s11x1221 x20002 x31012 x42022 x50102 x61112 x72122设信源(1) 求信源熵H(X);(2) 编二进制香农码和二进制费诺码;(3) 计算二进制香农码和二进制费诺码的平均码长和编码效率;(4) 编三进制费诺码;(5) 计算三进制费诺码的平均码长和编码效率;解:(1)(2)二进制香农码:x i p(x i)p a(x i)k i码字x1010x2210x33110x441110x5511110x66111110x771111110x871111111二进制费诺码:xi p(xi)编码码字k ix1001x210102x3101103x41011104x510111105x6101111106x71011111107 x8111111117 (3)香农编码效率:费诺编码效率:(4)x i p(x i)编码码字k i x1001 x2111 x320202 x41212x5202203 x612213 x72022204 x8122214(5)设无记忆二进制信源先把信源序列编成数字0,1,2,……,8,再替换成二进制变长码字,如下表所示.(1) 验证码字的可分离性;(2) 求对应于一个数字的信源序列的平均长度;(3) 求对应于一个码字的信源序列的平均长度;(4) 计算,并计算编码效率;(5) 若用4位信源符号合起来编成二进制哈夫曼码,求它的平均码长,并计算编码效率.序列数字二元码字1010000111001001310100001310110000141100有二元平稳马氏链,已知p(0/0) = ,p(1/1) = ,求它的符号熵.用三个符号合成一个来编写二进制哈夫曼码,求新符号的平均码字长度和编码效率.对题的信源进行游程编码.若“0”游程长度的截至值为16,“1”游程长度的截至值为8,求编码效率.选择帧长N= 64(1) 对00000000000000000000000000000000000000遍L-D码;(2) 对000000000010遍L-D码再译码;(3) 对0000000000000000000000000000000000000000000000000000000000000000遍L-D码;(4) 对0遍L-D码;(5) 对上述结果进行讨论.。



5.1某离散无记忆信源的概率空间为采用香农码和费诺码对该信源进行二进制变长编码,写出编码输出码字,并且求出平均码长和编码效率。
解:计算相应的自信息量1)()(11=-=a lbp a I 比特 2)()(22=-=a lbp a I 比特 3)()(313=-=a lbp a I 比特 4)()(44=-=a lbp a I 比特 5)()(55=-=a lbp a I 比特 6)()(66=-=a lbp a I 比特 7)()(77=-=a lbp a I 比特 7)()(77=-=a lbp a I 比特根据香农码编码方法确定码长1)()(+<≤i i i a I l a I平均码长984375.164/6317128/17128/1664/1532/1416/138/124/112/1L 1=+=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=由于每个符号的码长等于自信息量,所以编码效率为1。
费罗马编码过程5.2某离散无记忆信源的概率空间为使用费罗码对该信源的扩展信源进行二进制变长编码,(1) 扩展信源长度,写出编码码字,计算平均码长和编码效率。
(2) 扩展信源长度,写出编码码字,计算平均码长和编码效率。
(3) 扩展信源长度,写出编码码字,计算平均码长和编码效率,并且与(1)的结果进行比较。
解:信息熵811.025.025.075.075.0)(=--=lb lb X H 比特/符号 (1)平均码长11=L 比特/符号编码效率为%1.81X)(H 11==L η(2)平均码长为84375.0)3161316321631169(212=⨯+⨯+⨯+⨯=L 比特/符号 编码效率%9684375.0811.0X)(H 22===L η(3)当N=4时,序列码长309.3725617256362563352569442569242562732562732256814=⨯+⨯+⨯⨯+⨯⨯+⨯⨯+⨯+⨯⨯+⨯=L平均码长827.04309.34==L %1.98827.0811.0X)(H 43===L η可见,随着信源扩展长度的增加,平均码长逐渐逼近熵,编码效率也逐渐提高。

信息论与编码第5章第五章信源编码(第⼗讲)(2课时)主要内容:(1)编码的定义(2)⽆失真信源编码重点:定长编码定理、变长编码定理、最佳变长编码。
难点:定长编码定理、哈夫曼编码⽅法。
作业:5。
2,5。
4,5。
6;说明:本堂课推导内容较多,枯燥平淡,不易激发学⽣兴趣,要注意多讨论⽤途。
另外,注意,解题⽅法。
多加⼀些内容丰富知识和理解。
通信的实质是信息的传输。
⽽⾼速度、⾼质量地传送信息是信息传输的基本问题。
将信源信息通过信道传送给信宿,怎样才能做到尽可能不失真⽽⼜快速呢?这就需要解决两个问题:第⼀,在不失真或允许⼀定失真的条件下,如何⽤尽可能少的符号来传送信源信息;第⼆,在信道受⼲扰的情况下,如何增加信号的抗⼲扰能⼒,同时⼜使得信息传输率最⼤。
为了解决这两个问题,就要引⼊信源编码和信道编码。
⼀般来说,提⾼抗⼲扰能⼒(降低失真或错误概率)往往是以降低信息传输率为代价的;反之,要提⾼信息传输率常常⼜会使抗⼲扰能⼒减弱。
⼆者是有⽭盾的。
然⽽在信息论的编码定理中,已从理论上证明,⾄少存在某种最佳的编码或信息处理⽅法,能够解决上述⽭盾,做到既可靠⼜有效地传输信息。
这些结论对各种通信系统的设计和估价具有重⼤的理论指导意义。
§3.1 编码的定义编码实质上是对信源的原始符号按⼀定的数学规则进⾏的⼀种变换。
讨论⽆失真信源编码,可以不考虑⼲扰问题,所以它的数学描述⽐较简单。
图 3.1是⼀个信源编码器,它的输⼊是信源符号},,, {21q s s s S =,同时存在另⼀符号},,,{21r x x x X =,⼀般来说,元素xj 是适合信道传输的,称为码符号(或者码元)。
编码器的功能就是将信源符号集中的符号s i (或者长为N 的信源符号序列)变换成由x j (j=1,2,3,…r)组成的长度为l i 的⼀⼀对应的序列。
输出的码符号序列称为码字,长度l i 称为码字长度或简称码长。
可见,编码就是从信源符号到码符号的⼀种映射。

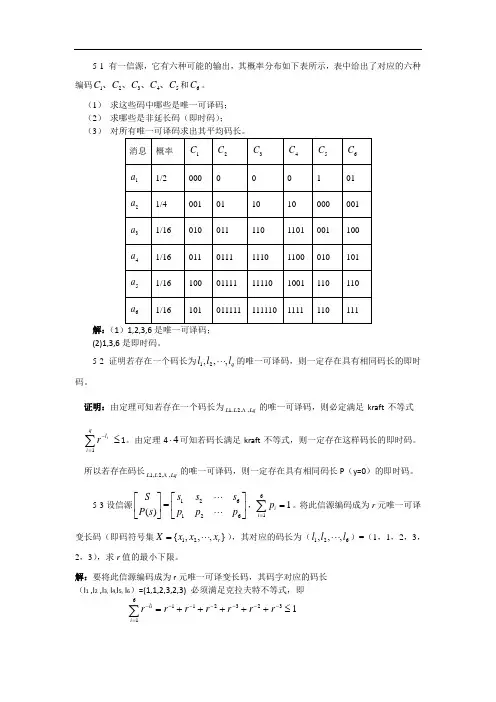
5-1 有一信源,它有六种可能的输出,其概率分布如下表所示,表中给出了对应的六种编码12345C C C C C 、、、、和6C 。
(1) 求这些码中哪些是唯一可译码; (2) 求哪些是非延长码(即时码);(3) 对所有唯一可译码求出其平均码长。
解:(1(2)1,3,6是即时码。
5-2证明若存在一个码长为12,,,q l l l ⋅⋅⋅的唯一可译码,则一定存在具有相同码长的即时码。
证明:由定理可知若存在一个码长为的唯一可译码,则必定满足kraft 不等式1。
由定理4可知若码长满足kraft 不等式,则一定存在这样码长的即时码。
所以若存在码长的唯一可译码,则一定存在具有相同码长P (y=0)的即时码。
5-3设信源126126()s s s S p p p P s ⋅⋅⋅⎡⎤⎡⎤=⎢⎥⎢⎥⋅⋅⋅⎣⎦⎣⎦,611i i p ==∑。
将此信源编码成为r 元唯一可译变长码(即码符号集12{,,,}r X x x x =⋅⋅⋅),其对应的码长为(126,,,l l l ⋅⋅⋅)=(1,1,2,3,2,3),求r 值的最小下限。
解:要将此信源编码成为 r 元唯一可译变长码,其码字对应的码长(l 1 ,l 2 ,l 3, l 4,l 5, l 6)=(1,1,2,3,2,3) 必须满足克拉夫特不等式,即132321161≤+++++=------=-∑r r r r r r ri liLq L L ,,2,1 ∑=-qi l ir1≤4⋅Lq L L ,,2,1所以要满足122232≤++r r r ,其中 r 是大于或等于1的正整数。
可见,当r=1时,不能满足Kraft 不等式。
当r=2, 1824222>++,不能满足Kraft 。
当r=3, 127262729232<=++,满足Kraft 。
所以,求得r 的最大值下限值等于3。
5-4设某城市有805门公务电话和60000门居民电话。
作为系统工程师,你需要为这些用户分配电话号码。


信息论与编码-曹雪虹-第五章-课后习题答案第五章(2) 哪些码是⾮延长码?(3) 对所有唯⼀可译码求出其平均码长和编译效率。
解:⾸先,根据克劳夫特不等式,找出⾮唯⼀可译码31123456231244135236:62163:22222216463:164:22421:2521:2521C C C C C C --------------?<+++++=<<++?=+?>+?<5C ∴不是唯⼀可译码,⽽4C :⼜根据码树构造码字的⽅法1C ,3C ,6C 的码字均处于终端节点∴他们是即时码(1) 因为A,B,C,D四个字母,每个字母⽤两个码,每个码为0.5ms, 所以每个字母⽤10ms当信源等概率分布时,信源熵为H(X)=log(4)=2平均信息传递速率为bit/ms=200bit/s(2) 信源熵为H(X)==0.198bit/ms=198bit/s5-541811613216411281128H(U)=1 2Log2() 14Log4() +18Log8() +116Log16 ()+132Log32 ()Log64()+1128Log128()+1128Log128()+ 1.984= (2) 每个信源使⽤3个⼆进制符号,出现0的次数为出现1的次数为P(0)=P(1)=(3)相应的费诺码(5)⾹农码和费诺码相同平均码长为编码效率为:5-11(1)信源熵(2)⾹农编码:平均码长:编码效率为(3)平均码长为:编码效率:4平均码长为:编码效率:5.16 已知⼆元信源{0,1},其p0=1/4,p1=3/4,试⽤式(4.129)对序列11111100编算术码,并计算此序列的平均码长。
解:根据算术编码的编码规则,可得:P(s=11111100) = P2(0)P6(1) = (3/4)6 (1/4)27)(1log =??=S P l根据(4.129)可得:F(S) = P(0) + P(10) + P(110) + P(1110) + P(11110) + P(111110) = 1–∑≥sy y P )(= 1 – P(11111111) – P(11111110) – P(11111101) – P(11111100)= 1– P(111111) = 1– (3/4)6 = 0.82202 = 0.110100100111⼜P(S) = A(S)= 0.0000001011011001,所以F(S) + P(S) = 0.1101010 即得C = 0.1101010 得S 的码字为1101010平均码长L 为 0.875。

信息论与编码曹雪虹第三版第五章1、在Windows 的"资源管理器" 窗口中,如果想一次选定多个分散的文件或文件夹,正确的操作是()。
[单选题] *A.按住Ctrl 键,用鼠标右键逐个选取B.按住Ctrl 键,用鼠标左键逐个选取(正确答案)C.按住Alt键,用鼠标右键逐个选取D.按住Alt键,用鼠标左键逐个选取2、72.在下列关于字符大小关系的说法中,正确的是()。
[单选题] *A.空格>a>AB.空格>A>aC.a>A>空格(正确答案)D.A>a>空格3、40.下列选项属于面向对象的程序设计语言是()。
[单选题] *A.Java和CB.Java和C++(正确答案)C.VB和CD.VB和Word4、76.计算机病毒的危害表现为()[单选题] *A.能造成计算机芯片的永久性失效B.使磁盘霉变C.影响程序运行,破坏计算机系统的数据与程序(正确答案)D.切断计算机系统电源5、在WPS表格中,关于筛选数据的说法正确的是()。
[单选题] *A.删除不符合设定条件的其它内容B.筛选后仅显示符合我们设定筛选条件的某一值或符合一组条件的行(正确答案)C.将改变不符合条件的其它行的内容6、执行删除操作时,()中的文件不能被送入回收站,而是直接删除。
[单选题] *A. C盘B. D盘C.U盘(正确答案)7、能够实现电子邮件服务器之间传输邮件的协议是()。
易[单选题] *A.DNSB.SNMPC.HTTPD.SMTP(正确答案)8、计算机硬件能直接识别和执行的只有()。
[单选题] *A.高级语言B.符号语言C.汇编语言D.机器语言(正确答案)9、把计算机网络看成是自治的计算机系统的集合,其中“自治的计算机”主要指()易[单选题] *A.可以独立运行的计算机(正确答案)B. 网络计算机C.裸机D. 网络终端10、在Internet 上,政府机构类别的域名中一般包括()。
第5章 有噪信道编码5.1 基本要求通过本章学习,了解信道编码的目的,了解译码规则对错误概率的影响,掌握两种典型的译码规则:最佳译码规则和极大似然译码规则。
掌握信息率与平均差错率的关系,掌握最小汉明距离译码规则,掌握有噪信道编码定理(香农第二定理)的基本思想,了解典型序列的概念,了解定理的证明方法,掌握线性分组码的生成和校验。
5.2 学习要点5.2.1 信道译码函数与平均差错率5.2.1.1 信道译码模型从数学角度讲,信道译码是一个变换或函数,称为译码函数,记为F 。
信道译码模型如图5.1所示。
5.2.1.2 信道译码函数信道译码函数F 是从输出符号集合B 到输入符号集合A 的映射:*()j j F b a A =∈,1,2,...j s =其含义是:将接收符号j b B ∈译为某个输入符号*j a A ∈。
译码函数又称译码规则。
5.2.1.3 平均差错率在信道输出端接收到符号j b 时,按译码规则*()j j F b a A =∈将j b 译为*j a ,若此时信道输入刚好是*j a ,则称为译码正确,否则称为译码错误。
j b 的译码正确概率是后验概率:*(|)()|j j j j P X a Y b P F b b ⎡⎤===⎣⎦ (5.1)j b 的译码错误概率:(|)()|1()|j j j j j P e b P X F b Y b P F b b ⎡⎤⎡⎤=≠==-⎣⎦⎣⎦ (5.2)平均差错率是译码错误概率的统计平均,记为e P :{}1111()(|)()1()|1(),1()|()s se j j j j j j j ssj j j j j j j P P b P e b P b P F b b P F b b P F b P b F b ====⎡⎤==-⎣⎦⎡⎤⎡⎤⎡⎤=-=-⎣⎦⎣⎦⎣⎦∑∑∑∑ (5.3)5.2.2 两种典型的译码规则两种典型的译码规则是最佳译码规则和极大似然译码规则。
第五章 信源编码(第十讲)(2课时)主要内容:(1)编码的定义(2)无失真信源编码 重点:定长编码定理、变长编码定理、最佳变长编码。
难点:定长编码定理、哈夫曼编码方法。
作业:5。
2,5。
4,5。
6;说明:本堂课推导内容较多,枯燥平淡,不易激发学生兴趣,要注意多讨论用途。
另外,注意,解题方法。
多加一些内容丰富知识和理解。
通信的实质是信息的传输。
而高速度、高质量地传送信息是信息传输的基本问题。
将信源信息通过信道传送给信宿,怎样才能做到尽可能不失真而又快速呢?这就需要解决两个问题:第一,在不失真或允许一定失真的条件下,如何用尽可能少的符号来传送信源信息;第二,在信道受干扰的情况下,如何增加信号的抗干扰能力,同时又使得信息传输率最大。
为了解决这两个问题,就要引入信源编码和信道编码。
一般来说,提高抗干扰能力(降低失真或错误概率)往往是以降低信息传输率为代价的;反之,要提高信息传输率常常又会使抗干扰能力减弱。
二者是有矛盾的。
然而在信息论的编码定理中,已从理论上证明,至少存在某种最佳的编码或信息处理方法,能够解决上述矛盾,做到既可靠又有效地传输信息。
这些结论对各种通信系统的设计和估价具有重大的理论指导意义。
§3.1 编码的定义编码实质上是对信源的原始符号按一定的数学规则进行的一种变换。
讨论无失真信源编码,可以不考虑干扰问题,所以它的数学描述比较简单。
图 3.1是一个信源编码器,它的输入是信源符号},,,{21q s s s S =,同时存在另一符号},,,{21r x x x X =,一般来说,元素xj 是适合信道传输的,称为码符号(或者码元)。
编码器的功能就是将信源符号集中的符号s i (或者长为N 的信源符号序列)变换成由x j (j=1,2,3,…r)组成的长度为l i 的一一对应的序列。
输出的码符号序列称为码字,长度l i 称为码字长度或简称码长。
可见,编码就是从信源符号到码符号的一种映射。
若要实现无失真编码,则这种映射必须是一一对应的,并且是可逆的。
码符号的分类: 下图是一个码分类图⎪⎪⎩⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧即时码(非延长码)非即时码唯一可译码非唯一可译码非奇异码奇异码分组码非分组码码下面,我们给出这些码的定义。
1. 二元码若码符号集为X={0;1},所有码字都是一些二元序列,则称为二元码。
二元码是数字通信和计算机系统中最常用的一种码。
2. 等长码:若一组码中所有码字的码长都相同,即l i =l(i=1,2,…q),则称为等长码。
3. 变长码:若一组码组中所有码字的码长各不相同,则称为变长码。
4. 非奇异码:若一组码中所有码字都不相同,则称为非奇异码。
5. 奇异码:若一组码中有相同的码字,则称为奇异码。
6. 唯一可译码:若码的任意一串有限长的码符号序列只能唯一地被译成所对应的信源符号序列,则此码称为唯一可译码,否则就称为非唯一可译码。
7. 非即时码和即时码:如果接收端收到一个完整的码字后,不能立即译码,还要等下一个码字开始接收后才能判断是否可以译码,这样的码叫做非即时码。
如果收到一个完整的码字以后,就可以立即译码,则叫做即时码。
即时码要求任何一个码字都不是其他码字的前缀部分,也叫做异前缀码。
码树:即时码的一种简单构造方法是树图法。
对给定码字的全体集合C={W 1,W 2,…W q }来说,可以用码树来描述它。
所谓树,就是既有根、枝,又有节点,如图 5.2(80业)所示,图中,最上端A 为根节点,A 、B 、C 、D 、E 皆为节点,E 为终端节点。
A 、B 、C 、D 为中间节点,中间节点不安排码字,而只在终端节点安排码字,每个终端节点所对应的码字就是从根节点出发到终端节点走过的路径上所对应的符号组成,如图5.2中的终端节点E ,走过的路径为ABCDE ,所对应的码符号分别为0、0、0、1,则E 对应的码字为0001。
可以看出,按树图法构成的码一定满足即时码的定义(一一对应,非前缀码)。
从码树上可以得知,当第i 阶的节点作为终端节点,且分配码字,则码字的码长为i 。
任一即时码都可以用树图法来表示。
当码字长度给定后,用树图法安排的即时码不是唯一的。
如图3.2中,如果把左树枝安排为1,右树枝安排为0,则得到不同的结果。
对一个给定的码,画出其对应的树,如果有中间节点安排了码字,则该码一定不是即时码。
每个节点上都有r 个分支的树称为满树,否则为非满树。
即时码的码树图还可以用来译码。
当收到一串码符号序列后,首先从根节点出发,根据接收到的第一个码符号来选择应走的第一条路径,再根据收到的第二个符号来选择应走的第二条路径,直到走到终端节点为止,就可以根据终端节点,立即判断出所接收的码字。
然后从树根继续下一个码字的判断。
这样,就可以将接收到的一串码符号序列译成对应的信源符号序列。
⏹克拉夫特(Kraft )不等式定理3.1 对于码符号为X={x 1,x 2,…x r }的任意唯一可译码,其码字为W 1,W 2,…W q ,所对应的码长为l 1,l 2…l q ,则必定满足克拉夫特不等式11≤∑=-qi l i r 反之,若码长满足上面的不等式,则一定存在具有这样码长的即时码。
注意:克拉夫特不等式只是说明唯一可译码是否存在,并不能作为唯一可译码的判据(可以排除,不能肯定)。
如{0,10,010,111}满足克拉夫特不等式,但却不是唯一可译码。
例题:设二进制码树中X={x 1,x 2,x 3,x 4},对应的l 1=1,l 2=2,l 3=2,l 4=3,由上述定理,可得18922222322141>=+++=----=-∑i l i 因此不存在满足这种码长的唯一可译码。
可以用树码进行检查。
⏹唯一可译码的判断法(变长):将码C 中所有可能的尾随后缀组成一个集合F ,当且仅当集合F 中没有包含任一码字,则可判断此码C 为唯一可译码。
集合F 的构成方法:首先,观察码C 中最短的码字是否是其它码字的前缀,若是,将其所有可能的尾随后缀排列出。
而这些尾随后缀又有可能是某些码字的前缀,再将这些尾随后缀产生的新的尾随后缀列出,然后再观察这些新的尾随后缀是否是某些码字的前缀,再将产生的尾随后缀列出,依此下去,直到没有一个尾随后缀是码字的前缀为止。
这样,首先获得了由最短的码字能引起的所有尾随后缀,接着,按照上述步骤将次短码字、…等等所有码字可能产生的尾随后缀全部列出。
由此得到由码C 的所有可能的尾随后缀的集合F 。
例题:设码C={0,10,1100,1110,1011,1101},根据上述测试方法,判断是否是唯一可译码。
解:1. 先看最短的码字:“0”,它不是其他码字前缀,所以没有尾随后缀。
2. 再观察码字“10”,它是码字“1011”的前缀,因此有尾随后缀。
所以,集合F={11,00,10,01},其中“10”为码字,故码C 不是唯一可译码。
§3.2 定长编码定理前面已经说过,所谓信源编码,就是将信源符号序列变换成另一个序列(码字)。
设信源输出符号序列长度为L ,码字的长度为K L ,编码的目的,就是要是信源的信息率最小,也就是说,要用最少的符号来代表信源。
在定长编码中,对每一个信源序列,K L 都是定值,设等于K ,我们的目的是寻找最小K 值。
要实现无失真的信源编码,要求信源符号X i (i=1,2,…q)与码字是一一对应的,并求由码字组成的符号序列的逆变换也是唯一的(唯一可译码)。
定长编码定理:由L 个符号组成的、每个符号熵为H L (X)的无记忆平稳信源符号序列X 1X 2X 3…X L 用K L 个符号Y 1Y 2…Y KL (每个符号有m 种可能值)进行定长变码。
对任意0,0>>δε,只要ε+≥)(log X H m LK L L则当L 足够大时,必可使译码差错小于δ;反之,当 ε2)(log -≤X H m LK L L时,译码差错一定是有限值,当L 足够大时,译码几乎必定出错。
式中,左边是输出码字每符号所能载荷的最大信息量所以等长编码定理告诉我们,只要码字传输的信息量大于信源序列携带的信息量,总可以实现几乎无失真的编码。
条件时所取得符号数L 足够大。
设差错概率为εP ,信源序列的自方差为22)]}()({[)(X x I E X i -=σ则有:22)(εσεL X P ≤ 当)(2X σ和2ε均为定值时,只要L 足够大,εP 可以小于任一整数δ,即δεσ≤22)(L X 此时要求:δεσ22)(X L ≥只要δ足够小,就可以几乎无差错地译码,当然代价是L 变得更大。
令m LK K Llog =为码字最大平均符号信息量。
定义编码效率为:KX H L )(=η 最佳编码效率为εη+=)()(X H X H L L无失真信源编码定理从理论上阐明了编码效率接近于1的理想编码器的存在性,它使输出符号的信息率与信源熵之比接近于1,但要在实际中实现,则要求信源符号序列的L 非常大进行统一编码才行,这往往是不现实的。
例如:例题:设离散无记忆信源概率空间为⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡04.005.006.007.01.01.018.04.087654321x x x x x x x x P X 信源熵为符号/55.2log )(812bit p p X H i i i =-=∑=自信息方差为82.7)]([)(log )]([log )(2)(log })]([log )(2){(log )](log [})]()({[)(812228181812222812222812222=-=++=++=--=-=∑∑∑∑∑∑======i i i i i i ii i i i i i i i i i i i X H p p p X H p p X H p p X H p X H p p X H p p X H x I E X σ对信源符号采用定长二元编码,要求编码效率%90=η,无记忆信源有)()(X H X H L =,因此%90)()(=+=εηX H X H可以得到28.0=ε如果要求译码错误概率610-≤δ,则872210108.9(≈⨯=≥δεσ)X L 由此可见,在对编码效率和译码错误概率的要求不是十分苛刻的情况下,就需要810=L 个信源符号一起进行编码,这对存储和处理技术的要求太高,目前还无法实现。
如果用3比特来对上述信源的8个符号进行定长二元编码,L=1,此时可实现译码无差错,但编码效率只有2.55/3=85%。
因此,一般说来,当L 有限时,高传输效率的定长码往往要引入一定的失真和译码错误。
解决的办法是可以采用变长编码。
§3.3 最佳编码最佳码:对于某一信源和某一码符号集来说,若有一唯一可译码,其平均码长K 小于所有其他唯一可译码的平均长度。