电磁学课后答案第四章

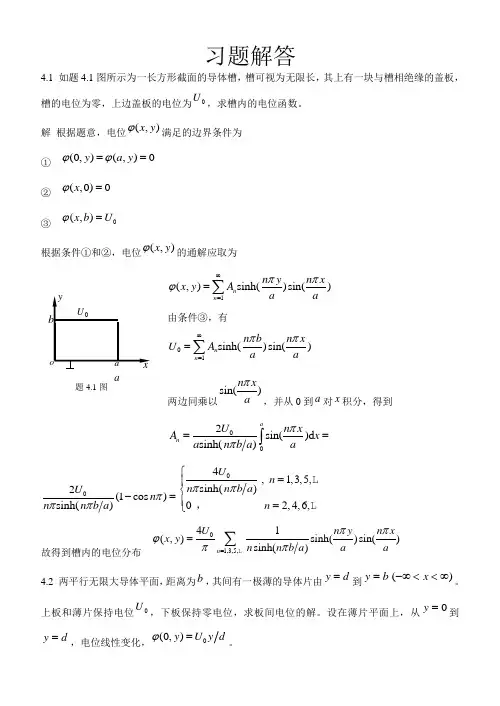
习题解答4.1 如题4.1图所示为一长方形截面的导体槽，槽可视为无限长，其上有一块与槽相绝缘的盖板，槽的电位为零，上边盖板的电位为U ，求槽内的电位函数。

解 根据题意，电位(,)x y ϕ满足的边界条件为 ① (0,)(,)0y a y ϕϕ== ② (,0)0x ϕ= ③0(,)x b U ϕ=根据条件①和②，电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a a ππϕ∞==∑由条件③，有01sinh()sin()n n n b n x U A a a ππ∞==∑两边同乘以sin()n x a π，并从0到a 对x 积分，得到002sin()d sinh()an U n xA x a n b a a ππ==⎰02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩L L ，故得到槽内的电位分布1,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a a ππϕππ==∑L4.2 两平行无限大导体平面，距离为b ，其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。

上板和薄片保持电位U ，下板保持零电位，求板间电位的解。

设在薄片平面上，从0=y 到d y =，电位线性变化，0(0,)y U y d ϕ=。

a题4.1图解 应用叠加原理，设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中，1(,)x y ϕ为不存在薄片的平行无限大导体平面间（电压为U ）的电位，即10(,)x y U y b ϕ=；2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位，其边界条件为： ①22(,0)(,)0x x b ϕϕ==②2(,)0()x y x ϕ=→∞③002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b d b ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩根据条件①和②，可设2(,)x y ϕ的通解为 21(,)sin()en x bn n n y x y A b ππϕ∞-==∑由条件③有00100(0)sin()()n n U U y y d n y b A U U b y yd y b d b π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n yb π，并从0到b 对y 积分，得到0002211(1)sin()d ()sin()d dbn d U U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d b ππ故得到 (,)x y ϕ=0022121sin()sin()e n x bn U bU n d n y y b d n b b ππππ∞-=+∑4.3 求在上题的解中，除开0U y 一项外，其他所有项对电场总储能的贡献。

4.3若半径为a 、电流为I 的无线长圆柱导体置于空气中，已知导体的磁导率为0μ，求导体内、外的磁场强度H 和磁通密度B 。

解：（1）导体内：0≤ρ<a由安培环路定理，⎰•ll d H='I'I =22.I a πρπ=22I a ρ 所以，21.22I H a ρπρ=，122I H a ρπ=，122I H e a ϕρπ→→=，011022I B H e a ϕμρμπ→→→==（2）导体外：a ≤ρ<+∞⎰•l l d H =I, 所以2.2H I πρ=,22I H e ϕπρ→→=，022I B e ϕμπρ→→=4.5 在下面的矢量中，哪些可能是磁通密度B ？如果是，与它相应的电流密度J 为多少？ （1）F a ρρ→→=解:1..()F F ρρρρ→∂∇=∂=1.2ρρ=2≠0所以F →不是磁通密度 （2）F →=-x a →y+y a →x 解：∇.F →=y x ∂-∂+xy ∂∂=0 所以F 是磁通密度 B →∇⨯=0μJ →=|x y ze e e x y zy x 0→→→∂∂∂∂∂∂-=2z e → 所以 J →=02μz e →（3）F →=x a →x —y a →y∇.F →=0F →是磁通密度B →∇⨯=0μJ →=|x y ze e e x y zx y→→→∂∂∂∂∂∂-=0所以J →=0 （4）F →=a ϕ→-r∇.F →=0所以F →是磁通密度B →∇⨯=r 2a a a r sin r sin rr 20r sin 0ϕθθθθϕθ→→→∂∂∂∂∂∂-=r a →-θcot +2a θ→=0μJ →所以J →=0cot θμ-r a →+02μa θ→ 4.6已知某电流在空间产生的磁矢位是A →=x a →2x y+y a →x 2y +z a →（2y —2z ） 求磁感应强度B →解：B →=A →∇⨯=|x y z2e e e x y z222x y xy y z →→→∂∂∂∂∂∂-=2y x e →+z e →（2y —2z ）4.13已知钢在某种磁饱和情况下的磁导率为1μ=20000μ，当钢中的磁通密度为B 1=0.5×102T ，1θ= 75°时，试求此时的磁力线由钢进入自由空间一侧后，磁通密度2B 的大小与2B 与法线的夹角2θ。

第四章 习题一(磁场)1、一根载有电流I 的无限长直导线，在A 处弯成半径为R 的圆形，由于导线外有绝缘层，在A 处两导线并不短路，则在圆心处磁感应强度B的大小为( C )(A) I (μ0＋1)／(2πR) (B) μ0πI ／(2πR) (C) μ0I(1＋π)／(2πR) (D) μ0I(1＋π)／(4πR)2、载有电流为I 的无限长导线，弯成如图形状，其中一段是半径为a 的半圆，则圆心处的磁感应强度B的大小为( D )(A) μ0I ／(4a ) + μ0I ／(4πa )(B))8/(2)4/()4/(a I a I a I o o o πμπμμ++(C) ∞(D))4/(2)4/()4/(a I a I a I o o o πμπμμ+-3、如图，电流I 均匀地自下而上通过宽度为a 的 无限长导体薄平板，求薄平板所在平面上距板的一 边为d 的P 点的磁感应强度。

解：该薄板可以看成是由许多无限长的细直载流 导线组成的，每一条载流线的电流为dI =Idx /a ， 根据无限长直载流线磁场公式，它们在P 点产 生的磁感应强度的大小为xdxa πI μx πdI μdB 2200==，B d 的方向⊗ ∴ dad a πI μx dx a πI μdB B a d d ad d+===⎰⎰++ln 2200，B 的方向⊗PB4、电流均匀地自下而上通过宽为2a 的无限长导体薄平板，电流为I ，通过板的中线并与板面垂直的平面上有一点P ，P 到板的垂直距离为x ，设板厚可略去不计，求P 点磁感应强度B 。

解：面电流线密度a I j 2/=在离轴线y 处取一宽为dy 的窄条，其电流为dy a Ijdy dI 2==, 22y x r +=P 点B d的方向如图所示。

r πdI μdB 20=220044yx dy a πI μr dy a πI μ+== 22cos sin yx x rx φθ+===，22sin cos yx y ry φθ+===2204cos y x ydya πI μθdB dB x +==，2204sin y x xdy a πI μθdB dB y+== 04220=+==⎰⎰--a a aa x x yx ydya πI μdB Bxaa πI μx y a πI μy x dy aπIx μdB B aa aa aa y y arctan 2arctan 4400220==+==---⎰⎰ y y y x x e x a aπIμe B e B B ⎪⎭⎫ ⎝⎛=+=arctan 205、求上题当a →∞，但维持aIj 2=(单位宽度上的电流，叫做电流线密度)为一常量时P 点的磁感应强度。

1.如图所示，一根细长的永磁棒沿轴向均匀磁化，磁化强度为。

试求图中表示的1、2、3、4、5、6、7各点的磁感应强度和磁场强度。

解永磁体被磁化，可以认为表面出现磁化电流，由磁化电流与磁化强度的关系，可知。

并且磁化电流产生的磁感应强度可与一细长螺线管产生的磁场等效，所以由细长螺线管磁场分布可知，在细长螺线管轴线上，其端部的磁感应强度恰为其中部的一半，故表明磁感应线连续。

因为沿方向的投影式为所以表明磁场不连续。

2有一圆柱形无限长载流导体，其相对磁导率为，半径为，今有电流沿轴线方向均匀分布，试求： 导体内任一点的 ； （2）导体外任一点的 ； （3）通过长为的圆柱体的纵截面的一半的磁通量。

解 （1）在导体内过距轴线为 的任一点作一个与轴垂直，圆心在轴线上，半径为 的圆周作为积分线路，如图所示。

此圆周与磁场线重合，而且沿圆周 是常数。

故得根据含介质的安培环路定理因导体内电流均匀分布，所以电流密度为在半径为 的截面中所以 ,则（2）在导体外任一点 ，以过这一点而圆心在轴线上的圆周作为积分线路，同样得因 ，故 ，所以 ,(3)如图所示，通过长为的圆柱体纵截面的一半的磁通量为3同轴电缆由两同心导体组成，内层是半径为的导体圆柱，外层是半径分别为、的导体圆筒，如图所示。

两导体内电流等量而反向，均匀分布在横截面上，导体的相对磁导率为,两导体间充满相对磁导率为的不导电的均匀磁介质。

试求在各区域中的分布。

解:对称性分析可知，在半径相等处的磁场强度大小相等，方向与电流方向成右手螺旋关系。

可用含介质时的安培环路定理求得，再由、之间的关系求得分布。

在中，,所以在中所以在中所以在中,, 各区域的方向与内层导体圆柱中的电流方向成右手螺旋关系。

4 一铁环外均匀绕有绝缘导线，导线中通有恒定电流，今若在环上开一条狭缝。

试求：（1）开狭缝前后，铁环中的，和如何变化；（2）铁环与缝隙中的，和。

解由高斯定理可知，磁场中磁感应强度总是闭合曲线，而磁场强度线却不一定连续；的环流是由回路中的传导电流决定的，而的环流是由回路中的传导电流和磁化电流（也称束缚电流）共同决定的。