基于主成分线性加权综合评价的信用评分方法及应用

主成分分析方法及其应用效果评估主成分分析（Principal Component Analysis，简称PCA）是一种常用的数据降维技术，被广泛应用于数据分析、模式识别和机器学习等领域。

本文将介绍主成分分析的基本原理、具体方法以及其在实际应用中的效果评估。

一、主成分分析的基本原理主成分分析是一种统计分析方法，旨在将具有相关性的多个变量转化为一组线性无关的新变量，称为主成分。

通过降维，主成分分析可以有效减少数据的维度，并保留原始数据中的大部分信息。

主成分分析的基本原理是通过找到数据中的最大方差方向来构建主成分。

具体步骤如下：1. 标准化数据：对原始数据进行标准化处理，使得每个变量具有相同的尺度。

2. 计算协方差矩阵：计算标准化后数据的协方差矩阵。

3. 计算特征值与特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。

4. 选择主成分：根据特征值的大小排序，选择前k个特征值对应的特征向量作为主成分。

5. 构建主成分：将选择的主成分按权重线性组合，得到原始数据的主成分。

二、主成分分析的具体方法主成分分析可以通过多种计算方法实现，其中最常用的是基于特征值分解的方法。

下面介绍主成分分析的具体计算步骤：1. 标准化数据：对原始数据进行标准化处理，使得每个变量具有均值为0、方差为1的特性。

2. 计算协方差矩阵：将标准化后的数据计算协方差矩阵。

3. 特征值分解：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。

4. 选择主成分：根据特征值的大小选择前k个特征向量作为主成分。

5. 构建主成分：将选择的主成分按权重线性组合，得到原始数据的主成分。

三、主成分分析在实际应用中的效果评估在应用主成分分析时，我们需要对其效果进行评估，以确保选择的主成分能够充分保留原始数据的信息。

常用的效果评估方法有以下几种：1. 解释方差比（Explained Variance Ratio）：解释方差比可以衡量每个主成分对原始数据方差的贡献程度。

基于主成分分析算法的信用评估模型研究一、引言信用评估是金融领域中的重要问题，它可以帮助银行和其他金融机构评估借款人的信用风险，以决定是否向其发放贷款。

随着金融信息化技术的发展，越来越多的金融机构开始采用机器学习方法进行信用评估，以提高评估质量和效率。

本文将介绍一种基于主成分分析算法的信用评估模型，并探讨其优缺点和应用前景。

二、背景传统的信用评估方法往往依赖于贷款人提供的财务和背景资料，这种方法的主要问题在于可能存在欺诈行为和数据不全等情况。

另一方面，随着互联网金融的兴起，越来越多的贷款人开始使用网络平台进行借贷，这种方式更加强调快速和便利，传统的信用评估方法已无法满足这种需求。

为了解决这一问题，机器学习方法逐渐应用于信用评估领域。

对于金融机构来说，使用机器学习方法可以帮助它们更好地评估借款人的信用风险，并提高贷款的成功率。

同时，对于借款人来说，使用机器学习方法不仅可以提高成功借贷的概率，还可以在一定程度上降低借贷成本。

三、主成分分析算法主成分分析算法又称为PCA，是最常用的无监督降维算法之一。

它的基本思想是找到一个新的坐标系，使得数据能够在新的坐标系下得到最大的方差。

具体方法是将高维数据映射到低维空间中，从而达到减少数据冗余的目的。

在信用评估中，我们可以将PCA算法应用于借款人的行为数据和信用历史数据。

例如，如果一个借款人在信用卡账单上有很高的滞纳金和逾期次数，那么这个行为可能代表着他的还款能力不足。

而如果借款人的信用历史记录中有很多欠款和违约记录，那么这个历史记录可能代表着他的信用worthiness低。

由此可以看出，PCA算法可以帮助Goldman Sachs等金融机构更好地评估借款人的信用worthiness。

其基本思想是将行为数据和信用历史数据分别表示为不同的特征，并将它们映射到低维空间中。

之后，评估模型将根据映射后的数据进行信用worthiness评估，并决定是否向该借款人发放贷款。

四、优缺点PCA算法有以下优点和缺点：优点：1. 可以有效减少数据冗余，提高数据的处理效率；2. 可以将高维数据映射到低维空间中，方便进行数据可视化和分析；3. 不需要任何先验知识或人工干预。

主成分分析在综合评价中的应用作者：王丽芳来源：《经济研究导刊》2012年第19期摘要：应用主成分分析原理，以较小的综合变量取代原有的多维变量，并且能客观的确定权数，避免主观随意性。

把原指标综合成几个主成分，再以这几个主成分的贡献率为权数构成加权平均，构造出一个综合评价函数。

给出了多指标复杂系统的排序方法，它排除了各指标间的相关性和量纲的不一致性，使系统信息不重叠，得到的排序结果合理可信。

关键词：主成分分析；综合评价；排序中图分类号：F22 文献标志码：A 文章编号：1673-291X（2012）19-0219-05引言排序问题在我们日常生活中经常碰到，对单指标系统中的各样本点进行排序，可按指标值的大小排序就可以了，而对多指标系统中的各样本点要进行排序就不能按各指标值的大小这一简单原则进行了，一个常用方法是对各指标进行总和平均后，按平均值的大小进行排序。

但有时由于各指标间的量纲不一样，就不能进行加法运算了。

再者，即使各指标间的量纲一致，可以作加法运算，而各指标反映系统侧面不同，对系统的作用不一样，作加法运算时，存在一个权系数的处理问题，而权系数的取定没有一个统一的标准，这样就不能得到统一的排序结果，同时，在很多情况下各指标间有一定的相关性，甚至是严重相关，从而使得这些指标所提供的信息在一定的程度上有所重叠，求和时系统信息会重叠计算，也不能得到令人信服的排序结果，本文利用主成分分析原理，对多维空间实行降维处理，在系统变异信息损失最小的情况下，得到线性无关的几个主成分，利用主成分得分，对系统中各样本点进行综合评价，这样就排除了各指标间由于量纲不同和信息重叠所造成的影响，不用人为规定权系数，排除主观因素的干扰，使得计算结果更加科学、真实可靠。

一、主成分分析法原理[1]设系统中各指标向量的均值为，协方差阵为，考虑线性组合：y1=l′1X=l11x1+l21x2+…+lp1xpy2=l′2x=l12x1+l22x2+…+lp2xp………………………………y p=l′pX=l1px1+l2px2+…+lppxp（1）由随机向量变换的性质，显然有：var（yi）=l′i∑li （i=1，2，…，p）cov（yi，yj）=l′i∑lj （i，j=1，2，…，p）在式（1）中的y1，y2，…，yp分别称为X=（x1，…，xp）′的第一主成分，第二主成分，…，第P主成分，如果它们满足：（1）yi与yj（i≠j）不相关；（2）y1是X的一切线性组合中方差达到最大的；y2是与y1不相关的一切X的线性组合中方差达到最大的，…，yi是与y1，…,yi-1（i=1，2，…，p）都不相关的一切X的线性组合中方差达到最大的。

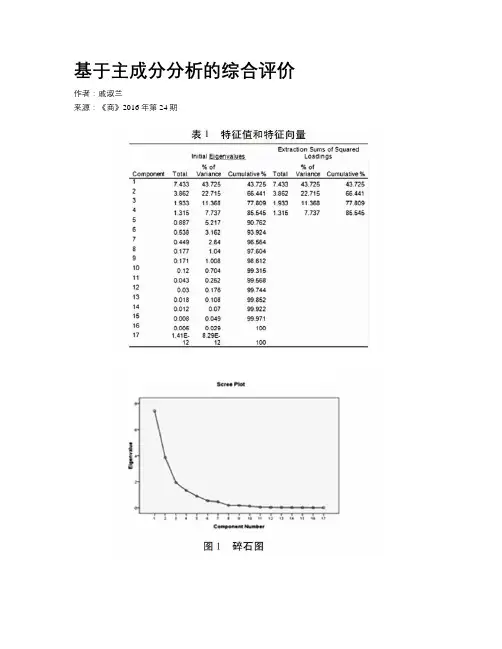
基于主成分分析的综合评价作者：戚淑兰来源：《商》2016年第24期摘要：研究综合评价研究问题关于社会、环境、经济等很多领域，是将事物的时效性，准确性，经济性以及满意性等方面进行评价的过程。

这要经过一定的途径将许多评价指标值合成一个综合性的评价指标值，从而进行综合评价。

主成分分析是一种重要的统计分析方法，它不仅可以想办法把原来很多具有一定相关关系的指标重新组合成一组新的且相互之间没有关系的指标，而且还能显示出比较客观的权重。

关键词：主成分分析；综合评价；环境污染；工业发展；spss.一、引言评价是一个综合咨询、计算和观测等方法的一个综合分析的过程。

但是这个过程需要评价者做出相应的指示。

综合评价就是将事物的准确性，时效性，经济性以及满意性等方面进行评价的过程。

但是评价者在评价这个过程中很容易主关干预，造成评价的结果偏离原来的结果。

多元统计分析是探讨多维变量总体，总体的每一个个体都可用p项指标来表示，虽然指标多能够描述详尽，显示细腻的一方面；但由于指标很多就较易造成分不清主次，对研究的对象很难做一个直接清楚的判断。

而主成分分析作为综合分析的一种统计方法，能够比较好的保证评价的结果是客观的。

主成分分析作为了一种比较科学的、客观的评价方法。

使综合评价的结果更加的科学，更加的实效。

二、研究背景人类的生产及生活过程与环境资源和生态环境有着很强的关系。

随着科学技术与经济的发展，人民生活水平的提高，工业的发达，废弃废料的排放造成很大程度的环境破坏和环境污染。

中国作为一个发展中国家，随着改革开放和经济的高速发展，环境污染也随之呈加剧之势。

经济发展与环境污染已经成为一个越来越重要的话题。

现在我们国家处于经济转型期，要把经济效益、环境保护以及产业结构相结合起来，形成经济新常态。

运用主成分分析综合评价的方法，寻找各省市经济发展、工业产值与环境污染状况之间的关系，而且对评价结论进行了解释。

三、主要思路经过探讨指标体系里面的结构关系就可以把许多个指标转换为相互之间没有关系的、含有初始指标的大部分内容的少数的几个综合性指标，运每个主成分的方差贡献率对那些指标加权得到综合评价得分。

基于主成分分析的综合评价模型在数据分析领域中，主成分分析（Principal Component Analysis，简称PCA）是一种常用的降维技术，它能够将高维的数据转化为较低维的数据，并保留数据的主要信息。

基于主成分分析的综合评价模型则是在PCA的基础上，对多个评价指标进行综合评价的模型。

本文将介绍基于主成分分析的综合评价模型的原理和应用。

一、主成分分析（PCA）简介主成分分析是一种通过线性变换将原始数据转化为低维空间的技术。

它通过找到数据中的主要方向，将数据投影到新的坐标系中，使得投影后的数据具有更好的可解释性和区分性。

主成分分析的基本步骤包括特征值分解、选择主成分和投影计算。

二、综合评价模型的构建方法基于主成分分析的综合评价模型的构建方法包括数据准备、特征值分解、主成分选择和综合评价计算。

首先，需要收集和整理待评价的指标数据，并进行归一化处理，以消除不同指标之间的量纲差异。

然后，对归一化后的指标数据进行特征值分解，得到特征值和特征向量。

接下来，选择主成分，可以根据特征值的大小顺序，选择前几个特征值对应的特征向量作为主成分。

最后，利用选定的主成分对原始指标数据进行投影，得到综合评价结果。

三、基于主成分分析的综合评价模型的应用举例以某酒店为例，我们希望对其服务质量进行综合评价。

我们收集了以下几个指标作为评价依据：员工态度、服务速度、设施条件和价格水平。

首先，对这些指标进行归一化处理，然后进行特征值分解。

假设得到的特征值分别为λ1、λ2、λ3、λ4，对应的特征向量分别为v1、v2、v3、v4。

根据特征值的大小顺序，我们选择前两个特征值对应的特征向量作为主成分。

然后，我们利用选定的主成分对原始指标数据进行投影计算，得到综合评价结果。

假设原始指标数据为X1、X2、X3、X4，对应的投影结果为Y1、Y2。

最后，通过采用某种评分方法，将投影结果转化为能够描述酒店服务质量的综合评价得分。

四、基于主成分分析的综合评价模型的优势与不足基于主成分分析的综合评价模型具有以下优势：首先，可以将多个指标融合为一个综合指标，简化评价过程；其次，可以消除不同指标之间的量纲差异，减小指标权重确定的困难。

主成分分析主成分计算综合评分公式主成分分析的基本原理是寻找一个新的坐标系，使得数据在新坐标系下的方差最大化。

这个新坐标系的基向量称为主成分，是原始数据向量的线性组合。

主成分分析的目标是找到一个转换矩阵，将原始数据映射到主成分空间，从而找到最能代表原始数据特征的主成分。

主成分的计算可以通过协方差矩阵的特征值分解来实现。

设原始数据矩阵为X，其中每一行为一个样本，每一列为一个特征。

首先，计算原始数据的均值向量μ，然后将每个特征减去其均值，得到零均值的数据矩阵X'。

接着，计算协方差矩阵C=1/(n-1)*X'*X'的转置，其中n为样本数量。

对协方差矩阵进行特征值分解，得到特征值λ和特征向量V。

按照特征值从大到小的顺序排列特征向量，选取前k个特征向量构成主成分，其中k为降维后的维度。

主成分得分的计算可以通过原始数据矩阵和主成分矩阵的乘积来实现。

设主成分矩阵为P=[v1,v2,...,vk]，其中vi为第i个主成分的特征向量，原始数据矩阵为X，由n个样本组成。

则主成分得分矩阵为Y=X*P，其中Y的每一行对应一个样本在主成分空间的坐标。

综合评分公式是一种基于主成分分析结果计算样本综合得分的方法。

在主成分分析中，主成分可以看作是原始数据中的一种变化，反映了数据样本在不同方向上的变化程度。

综合评分可以通过将每个主成分乘以其贡献率得到，然后对结果求和，从而综合反映各主成分对样本的影响程度。

具体而言，设主成分向量为v=[v1,v2,...,vk]，其贡献率为λ=[λ1,λ2,...,λk]，样本数据矩阵为X，其中每一行为一个样本。

主成分得分矩阵为Y=X*P，综合评分向量为Z=Y*v。

综合评分Z可以表示为Z=z1*v1+z2*v2+...+zk*vk，其中zi为第i个主成分的得分，vi为第i 个主成分的向量。

这样，综合评分Z即为将各主成分的得分按照其贡献率加权求和得到的结果。

综合评分公式的计算可以通过以下步骤实现：1.计算主成分矩阵P和贡献率向量λ；2.计算主成分得分矩阵Y=X*P；3.计算综合评分矩阵Z=Y*v，其中v为主成分矩阵；4.对综合评分矩阵Z的每一行求和，即可得到样本的综合评分。

主成分分析及其在统计综合评价系统中的应用一. 文献综述主成分分析法是在对于复杂系统进行统计分析时十分有效的一种方法。

本文主要是对主成分分析法进行详细介绍，并分析其在统计综合评价中的应用[1]。

突出介绍主成分分析法在学生综合成绩分析[2]、企业业绩分析[3]及景区游客服务满意度测评[4]这三个综合评价系统中的应用。

并在文末，对主成分分析法进行了一定的改进[5]，使得主成分分析法更加合理并贴近实际，且在一定程度上减小了统计分析过程中“线性化”产生的误差。

二.相关知识在我们进行系统分析时，多变量问题是经常会遇到的。

变量太多，无疑会增加分析问题的难度与复杂性，而且在许多实际问题中，多个变量之间是具有一定的相关关系的。

因此，我们就会很自然地想到，能否在各个变量之间相关关系研究的基础上，用较少的新变量代替原来较多的变量，而且使这些较少的新变量尽可能多地保留原来较多的变量所反映的信息？事实上，这种想法是可以实现的，本文介绍的主成分分析方法就是综合处理这种问题的一种强有力的方法。

（一）主成分分析方法的原理主成分分析是把原来多个变量化为少数几个综合指标的一种统计分析方法，从数学角度来看，这是一种降维处理技术。

假定有n个样本，每个样本共有p个变量描述，这样可构成一个n×p阶的数据矩阵。

如何从这么多变量的数据中抓住事物的内在规律性呢？要解决这一问题，自然要在p维空间中加以考察，这是比较麻烦的。

为了克服这一困难，就需要进行降维处理，即用较少的几个综合指标来代替原来较多的变量指标，而且使这些较少的综合指标既能尽量多地反映原来较多指标所反映的信息，同时它们之间又是彼此独立的。

那么，这些综合指标（即新变量)应如何选取呢？显然，其最简单的形式就是取原来变量指标的线性组合，适当调整组合系数，使新的变量指标之间相互独立且代表性最好。

如果记原来的变量指标为，它们的综合指标——新变量指标为，（m≤p)。

则在（1)式中，系数由下列原则来决定：（1)与相互无关；（2)是的一切线性组合中方差最大者；是与不相关的的所有线性组合中方差最大者；……；是与都不相关的的所有线性组合中方差最大者。

基于线性加权的综合评价法在输油管布置问题上的应用【摘要】本文通过综合评价法在输油管布置问题上的应用展开讨论。

首先介绍了研究背景、研究目的和研究意义，明确了研究的重要性。

然后对输油管布置问题进行了概述，说明了其在能源领域的重要作用。

接着介绍了基于线性加权的综合评价法的原理和方法，详细阐述了其在输油管布置问题中的应用。

通过案例分析，展示了该方法的实际效果，并对其优缺点进行了分析。

最后对基于线性加权的综合评价法在输油管布置问题上的应用进行了总结，同时展望了未来的研究方向。

本文为相关领域的研究提供了有益的参考和借鉴。

【关键词】线性加权、综合评价法、输油管布置、案例分析、优缺点分析、研究背景、研究目的、研究意义、结论、展望未来、研究方向。

1. 引言1.1 研究背景输油管布置问题是输油工程中重要的问题之一，其合理布置可以提高输油效率、降低运输成本，并且对环境保护具有重要意义。

随着输油工程规模的不断扩大和投资的增加，如何在满足输油需求的同时兼顾成本和环境因素成为了研究重点。

传统的输油管布置方案多基于经验和专家经验，缺乏科学依据和系统评价方法。

研究人员开始将多种评价方法引入输油管布置问题中，以提高决策的科学性和准确性。

基于线性加权的综合评价法是一种常用的决策方法，通过对各种因素进行加权处理，综合考虑各因素之间的关联性，得出最优的方案。

本研究旨在探讨基于线性加权的综合评价法在输油管布置问题上的应用，为输油工程决策提供科学依据和方法支持。

通过对该方法的分析和评价，可以为输油工程的优化设计和运营管理提供重要的参考依据。

1.2 研究目的研究的目的是通过基于线性加权的综合评价法来解决输油管布置问题，提高输油管线的布置效率和可靠性。

具体来说，通过对输油管线布置问题进行综合评价，确定最佳的管线布置方案，以降低输油管线的运行成本、减少环境影响，并提高输油系统的安全性和可靠性。

研究的目的还包括探讨基于线性加权的综合评价方法在输油管布置问题中的适用性和有效性，为实际工程应用提供参考和指导。

基于主成分分析模型的我国商业银行绩效评估一、商业银行绩效评估的意义商业银行作为金融机构，在国民经济中扮演着重要的角色。

其绩效评估直接关系到金融市场的稳定和国民经济的发展。

通过绩效评估，可以更好地了解商业银行的经营状况，为监管部门提供参考依据，同时也可以为商业银行的内部管理和运营决策提供重要参考意见。

商业银行绩效评估的意义重大。

二、主成分分析模型在绩效评估中的应用主成分分析模型是一种常用的多元统计方法，其主要目的是通过将原始变量进行线性变换，得到一组新变量，这些新变量称为主成分。

主成分能够尽可能多地概括原始变量的信息，减少变量之间的相关性，从而实现降维和信息提取的目的。

在商业银行绩效评估中，主成分分析模型可以帮助我们从众多指标中提取出关键的绩效特征，为评估提供便利。

三、我国商业银行绩效评估的指标体系在商业银行绩效评估的指标体系中，通常包括了财务指标、运营效率指标、风险管理指标等多个方面。

财务指标包括资产负债率、净利润率、不良贷款率等；运营效率指标包括利润率、资产利润率、存款利润率等；风险管理指标包括资本充足率、两个月逾期贷款率、拨备覆盖率等。

这些指标综合反映了商业银行资产质量、盈利能力和风险管理水平等方面的情况。

四、基于主成分分析模型的我国商业银行绩效评估实证分析以某省份5家商业银行为研究对象，进行了基于主成分分析模型的绩效评估实证分析。

选取了10个代表性的绩效指标进行主成分分析，得到了3个主成分。

然后，利用主成分得分进行了实证研究和评价。

通过实证研究，我们发现不同商业银行的绩效表现存在较大差异，同时也发现了各家商业银行的绩效特点和问题所在。

某家商业银行的主要问题在于风险管理水平不佳，另一家商业银行的主要问题在于盈利能力较弱。

通过主成分分析模型，我们可以更清晰地了解商业银行的绩效特征和问题所在。

五、完善我国商业银行绩效评估体系的建议基于以上分析，我们提出以下建议，以完善我国商业银行绩效评估体系：一是应该加强对非财务指标的采集和利用，在绩效评估中不仅应该关注财务指标，还应该重视运营效率和风险管理指标，以全面评价商业银行的绩效；二是应该进一步细化评价指标和加强动态性分析，绩效评估体系需要不断改进和完善，以适应金融市场的变化和发展；三是应该建立统一的评价标准和指标权重，对于商业银行绩效评估，需要建立一套统一的评价标准和指标权重，以确保评价的客观性和公正性。

主成分综合评价模型引言：主成分综合评价模型是一种常用的多指标综合评价方法，可以用于评估和比较不同对象或方案的综合性能。

本文将介绍主成分综合评价模型的基本原理、应用领域以及优缺点，并结合实际案例进行说明。

一、主成分综合评价模型的基本原理主成分综合评价模型是一种基于统计学原理的多指标综合评价方法。

首先，通过对多个指标的测量或观测，计算得到各个指标的原始数据。

然后，通过主成分分析方法，将这些指标进行综合，得到一组主成分。

最后，根据主成分的贡献率，对不同对象或方案进行综合评价。

主成分分析是一种降维技术，通过线性变换将原始数据转化为一组互相无关的主成分。

主成分的选择是基于其解释方差的能力，通常选择前几个主成分，使其累计贡献率达到一定阈值。

主成分的计算和选择可以使用各种统计软件进行实现。

二、主成分综合评价模型的应用领域主成分综合评价模型在各个领域都有广泛的应用，包括经济、环境、工程、管理等方面。

以下是几个常见的应用领域：1. 经济领域：主成分综合评价模型可以用于评估不同地区或国家的经济发展水平。

通过选取合适的经济指标，如GDP、人均收入、失业率等，可以对不同地区或国家的经济综合实力进行比较和评价。

2. 环境领域：主成分综合评价模型可以用于评估环境质量。

通过选取合适的环境指标，如空气质量指数、水质指标、土壤污染程度等，可以对不同地区或场所的环境质量进行综合评价。

3. 工程领域：主成分综合评价模型可以用于评估工程项目的综合效益。

通过选取合适的评价指标，如投资回报率、工期、质量等，可以对不同工程项目进行综合评价，从而帮助决策者做出合理的决策。

4. 管理领域：主成分综合评价模型可以用于评估企业或组织的综合绩效。

通过选取合适的绩效指标，如销售额、利润率、员工满意度等，可以对不同企业或组织的综合绩效进行比较和评价，从而指导管理决策。

三、主成分综合评价模型的优缺点主成分综合评价模型具有以下优点：1. 可以综合考虑多个指标的信息，避免了单一指标评价的局限性。

四川农业大学商学院课程论文《数据处理方法》课程论文论文题目：主成分分析在综合评价中的应用成员1：工作：分数：成员2：工作：分数：成员3：工作：分数：成员4：工作：分数：2013-5-14主成分分析在综合评价中的应用摘要本文根据2007年各地区国有及国有控股工业企业主要经济效益指标的统计数据，进行主成分分析并选取三个主成分，运用主成分对各地区进行综合排名。

运用K均值聚类，得出的结果与主成分综合排名进行比较，结果相当吻合，主成分分析可广泛运用于经济指标数据分析。

关键字：主成分分析经济效益指标综合排名分类Application of Principal Component Analysis in the analysis of Economic Data Xionghao, Information and Computing Science, 20109271Yang Xiaotao, Information and Computing Science, 20109281Zou Huimin, Financial Management, 20118795Zhao Wenqin, Financial Management, 20118793Abstract: according to the 2007 state-owned and state holding industrial enterprises in various areas of the main economic benefit index statistics, principal component analysis and three principal components and using the principal component comprehensive ranking for all regions. Using k-means clustering, and the results comparing with principal component comprehensive ranking and the results are consistent, principal component analysis data analysis can be widely used in economic indicators.Key words: principal component analysis ;Comprehensive ranking ;Classification1.问题描述经济数据分析结果对国家的宏观调控与企业决策有着至关重要的作用。

基于主成分分析模型的我国商业银行绩效评估随着我国经济的不断发展，商业银行作为金融体系中的重要组成部分，其扮演着极为重要的角色。

商业银行的绩效评估，直接关系到金融体系的稳定和经济的发展。

对商业银行的绩效进行科学客观的评估成为当务之急。

本文将基于主成分分析模型，探讨我国商业银行的绩效评估方法，并提出了一种基于主成分分析模型的我国商业银行绩效评估方法。

主成分分析（Principal Component Analysis, PCA）是一种常用的多元统计分析方法，能够从多个指标中提取出少数几个综合指标，用以反映原始指标所包含的综合信息。

在研究商业银行绩效评估时，我们可以通过主成分分析模型，将众多指标化解为少数几个综合指标，用以评估商业银行中的绩效状况。

主成分分析模型能够充分挖掘指标间的信息，简化指标体系，提高评估的效率和准确性。

我国商业银行的绩效评估指标多种多样，包括资产负债率、资本充足率、不良贷款率、息差、资金成本、资产利润率等。

将这些指标进行主成分分析，我们能够将这些指标综合起来，形成一个更为全面客观的绩效评估指标体系。

我们需要确定评估对象。

我国商业银行众多，不同规模、不同性质、不同地区的商业银行在绩效上存在差异。

我们需要针对不同类型的商业银行，建立相应的绩效评估模型。

我们需要确定评估指标。

我们可以根据商业银行的特点和发展阶段，选择适当的指标作为评估指标，例如对于新兴的商业银行，我们可以关注其成长性和风险抵御能力，对于成熟的商业银行，我们可以更多关注其盈利能力和风险控制水平。

然后，我们利用主成分分析模型对这些指标进行综合评估。

主成分分析模型能够将多个指标综合起来，形成一个更为全面客观的绩效评估指标。

通过主成分分析，我们可以得出少数几个综合指标，用以评估商业银行的绩效状况。

这些综合指标既考虑了不同指标的重要性，也减少了指标间的相关性对评估结果的影响。

我们可以根据得到的综合指标，对商业银行的绩效进行评估和排名。

基于主成分分析的综合评价研究一、本文概述主成分分析（Principal Component Analysis, PCA）作为一种多元统计分析方法，通过线性变换将原始数据集中的多个相互关联的变量转换为少数几个互不相关的主成分，从而实现对数据集的降维处理。

这一方法既简化了数据结构，又保留了原始数据中的主要信息，因此在多个领域得到了广泛应用。

本文旨在探讨基于主成分分析的综合评价研究，通过深入分析和研究主成分分析的理论基础、应用方法及其在综合评价中的实际应用，以期为相关领域的研究和实践提供有益的参考和启示。

本文将对主成分分析的基本理论进行梳理和阐述，包括主成分分析的基本原理、数学模型、计算方法以及优缺点等。

在此基础上，进一步探讨主成分分析在综合评价中的应用方法和步骤，包括评价指标体系的构建、数据的预处理、主成分的计算和解释以及最终评价结果的生成等。

本文将以实际案例为基础，分析主成分分析在综合评价中的具体应用和效果。

通过对案例的深入剖析，展示主成分分析在解决实际问题中的有效性和实用性，同时也探讨其在应用中可能存在的局限性和挑战。

本文将对主成分分析在综合评价中的未来发展进行展望，探讨其在新技术、新方法不断涌现的背景下如何与其他方法相结合，进一步提高综合评价的准确性和有效性。

也期望通过本文的研究，能够激发更多学者和实践者对主成分分析在综合评价中的研究和应用兴趣，共同推动该领域的发展和进步。

二、主成分分析基本理论主成分分析（Principal Component Analysis，PCA）是一种广泛使用的统计方法，它通过线性变换将原始数据集中的多个相关变量转化为少数几个独立的综合变量，这些新的综合变量称为主成分。

主成分分析旨在减少数据集的维度，同时保留数据中的主要变化特征。

方差最大化：主成分分析通过寻找数据集中方差最大的方向来提取主成分。

方差越大，说明该主成分包含的信息量越多，对数据集的代表性也越强。

协方差为零：主成分之间是相互独立的，即它们的协方差为零。

主成分分析法在公司综合评价中的应用文章主要介绍了主成分分析法的基本思想和计算步骤，并用主成分分析法在公司综合评价方面进行了实证分析。

标签：主成分分析法指标综合评价目前国内外关于多指标综合评价的方法很多，根据权重确定方法的不同，大致可分为两类：一类是主观赋权法，如层次分析法、德尔菲法，等等，多是采用综合咨询评分的定性方法。

这类方法因受到人为因素的影响，往往会夸大或降低某些指标的作用，致使排序的结果不能完全真实地反映事物间的现实关系。

另一类是客观赋权法，即根据各指标间的相关关系或各项指标值的变异程度来确定权数，避免由于人为因素带来的偏差，如主成分分析法、因子分析法，等等。

本文介绍的主成分分析法在将原始变量转变为主成分的过程中，同时形成了反映主成分和指标包含信息量的权数，以计算综合评价值。

这样在指标权重选择上克服了主观因素的影响，客观地反映了样本间的现实关系。

一、主成分分析法的基本思想和分析步骤主成分分析就是设法将原来众多的具有一定相关性的指标(比如P个指标)，重新组合成一组新的相互无关的综合指标来代替原来的指标。

通常数学上的处理就是将原来P个指标作线性组合，若没有限制条件作为新的综合指标，这样的线性组合会有很多，那么如何去选取呢?主成分分析的基本思想是：如果将选取的第一个线性组合即第一个综合指标记为F1，自然希望尽可能多的反映原来指标的信息。

这里的“信息”最经典的方法就是用F1的方差来表达，即Var(F1)越大，表示F1包含的信息越多。

因此在所有的线性组合中所选取的F1应该是方差最大的，故称F1为第一主成分。

如果第一主成分不足以代表原来P个指标的信息，再考虑选取F2 即选第二个线性组合,为了有效地反映原来信息,F1已有的信息就不再需要出现在F2中，用数学语言表达就是要求Cov(F1,F2)=0,称F2为第二主成分，依次类推可以造出第三，第四…第P个主成分。

不难想象这些主成分之间不仅不相关，而且它们的方差依次递减，因此在实际工作中，就挑选前几个最大主成分。

线性加权综合法在药品供应商评价中的应用引言药品供应商是药品生产、流通和销售的重要组成部分，其服务质量和信誉度对于整个药品行业的发展具有重大意义。

因此，药品供应商的评价是非常重要的。

在药品供应商评价中，使用线性加权综合法可以更准确地反映供应商在多个方面的表现，使评价结果更客观。

线性加权综合法线性加权综合法是一种常用的综合评价方法，它根据不同指标的权重值对多个指标进行加权求和，得出一个总评价值。

其计算公式如下：总评价指数= Σ（权重值 × 标准化后的指标值）其中，权重值表示指标的重要程度，标准化后的指标值可以将不同指标的不同量纲统一化。

药品供应商评价指标药品供应商的评价指标可以综合考虑供应商道德、价格、质量、配送、售后等多个方面。

下面是一些可能用到的指标和其相应的权重值：指标权重值正面评价数0.3产品价格0.15产品质量0.25配送速度0.2售后服务0.1这些指标的权重值可以根据实际情况进行调整。

线性加权综合法在药品供应商评价中的应用下面以一个实例来说明线性加权综合法在药品供应商评价中的应用。

某医院需要对两家药品供应商进行评价，假设它们在正面评价数、产品价格、产品质量、配送速度和售后服务等方面得分如下：供应商正面评价数产品价格产品质量配送速度售后服务总评价分数A供应商8 4.5 3.3 4 4.7 4.09B供应商 6 4 4.5 4.5 3.8 4.04则可以根据上面所述的线性加权综合法，计算两家供应商的总评价分数。

其中，正面评价数的权重值为0.3，价格的权重值为0.15，质量的权重值为0.25，配送速度的权重值为0.2，售后服务的权重值为0.1。

首先，对各个指标进行标准化处理，使得各个指标的值在同一量纲下：供应商正面评价数产品价格产品质量配送速度售后服务A供应商0.533 0.750 0.550 0.800 0.940B供应商0.400 0.667 0.750 1.000 0.760然后，根据上述公式计算两家供应商的总评价分数：A供应商的总评价分数 = 0.3 × 0.533 + 0.15 × 0.750 + 0.25 × 0.550 + 0.2 × 0.800 + 0.1 × 0.940 = 0.673B供应商的总评价分数 = 0.3 × 0.400 + 0.15 × 0.667 + 0.25 × 0.750 + 0.2 × 1.000 + 0.1 × 0.760 = 0.646因此，根据综合评价结果，A供应商在多方面的表现更好，是优选的药品供应商。

基于线性加权的综合评价法在输油管布置问题上的应用随着现代工业的发展，输油管布置问题日益成为一个备受关注的话题。

输油管网的合理布置是确保油气运输安全高效的重要因素之一。

为了解决输油管布置问题，用多维度的指标对候选方案进行评价和比较，一种常用的方法是基于线性加权的综合评价法，该方法基于对各项指标的重要性进行加权求和，得到最终方案的评价分数，从而确定最佳布置方案。

本文将探讨基于线性加权的综合评价法在输油管布置问题上的应用，分析其优缺点，并结合实际案例进行讨论。

2. 基于线性加权的综合评价方法的优点线性加权的综合评价方法具有以下优点：（1）简单易行：线性加权的综合评价方法不需要过多的数学理论和计算，只需对各项指标进行重要性的排序和确定权重，然后进行加权求和即可得到评价结果，操作简单方便。

（2）直观易懂：线性加权的综合评价方法对各项指标的重要性进行了明确的权重分配，最终得到的评价分数直观地反映了各方案的优劣程度，便于决策者进行权衡和选择。

（3）适用性广泛：线性加权的综合评价方法适用于各种多指标决策问题，包括输油管布置问题在内，对各种类型的指标、各种类型的方案都具有较好的适用性。

3. 基于线性加权的综合评价方法的缺点线性加权的综合评价方法也存在一些缺点：（1）权重确定困难：确定各项指标的重要性权重是线性加权的核心，但往往由于主观与客观因素的综合影响，权重的确定往往较为困难，且容易受到专家经验和主观意识的干扰。

（2）忽略指标间的相互关系：线性加权的综合评价方法直接对各项指标进行加权求和，忽略了指标之间的相互关系和相互影响，可能导致评价结果的片面性和不够全面性。

（3）结果的敏感性差：由于线性加权的综合评价方法对各项指标的加权求和直接线性叠加，对指标的变化不够敏感，导致评价结果的稳定性和灵活性不足。

基于线性加权的综合评价方法在输油管布置问题上有着一定的应用前景，可以为输油管布置问题的决策提供科学的依据和参考。

在实际应用中，也需要注意权重确定的准确性和评价结果的可靠性，充分发挥线性加权的综合评价方法的优势，同时针对其缺点进行进一步的探讨和改进，以提高其在输油管布置问题上的应用效果和价值。

信用评分算法的设计和应用一、概述信用评分是指通过对借款人的信用背景、信用历史、个人情况等进行综合评估，从而确定其偿还借款的风险性以及借款额度和利率等相关事宜。

信用评分的设计和应用在金融业、保险业、电商等领域中广泛应用。

二、常见的信用评分算法1.经典评分卡模型经典评分卡模型是目前应用最广泛的信用评分模型之一。

其基本原理是通过建模分析来识别与风险相关的特征因素，进而设计出可信度较高、能够预测未来行为的评分卡。

评分卡通常包含多个评分因素和相应的评分标准，将借款人的信用评分结果划分为相应的评级，以此来评估借款人的信用风险。

2.逻辑回归模型逻辑回归模型是另一种常见的信用评分算法。

逻辑回归模型通过建立一个逻辑方程来预测未来的事情发生概率。

逻辑方程基于借款人的特征因素，例如年龄、收入等，对借款人进行分类得分，以此来预测其是否有偿还借款的能力。

3.神经网络模型神经网络模型是一种基于生物神经系统的信用评分算法。

神经网络模型通过对整个数据集进行训练，从而预测未来的信用风险。

神经网络模型具有较强的泛化能力，能够有效地处理海量数据，适用于大规模信用评分体系的实现。

三、信用评分算法的设计要素1.选择合适的评分模型评分模型的选择直接决定了评分结果的准确性和信度。

因此，在选择评分模型时，应根据评分目的、数据样本量、评级分布、变量相关性、欠拟合与过拟合等因素进行权衡。

2.合理选择评分因素评分因素是决定评分结果的关键因素。

要选择最合适的评分因素，需要根据行业特点、评分模型的特点等进行综合考虑。

常用的评分因素包括借款人个人基本信息、财务状况、信用历史、用途和背景等。

3.构建可靠的评分卡评分卡是信用评分模型的核心，也是决定评分结果的关键因素。

在构建评分卡时，应注意评分卡的可信度、可解释性、可操作性和可更新性等方面，以便满足不同的应用场景需求。

四、信用评分算法的应用实践1.金融领域在金融领域，信用评分算法被广泛应用于贷款申请、信用卡申请、资产管理、保险等方面。

消费者信用评估中的PCALWM方法研究李建平1,2，徐伟宣2(1.中国科学技术大学商学院，安徽合肥，230026; 2.中科院科技政策与管理科学研究所，北京 100080)摘要：设计了一种基于主成分线性加权模型(PCALWM)的消费者信用评估方法，具有评估的客观性、可行性、适应性等优点。

使用真实信用卡数据的实证检验表明模型分类效果比较好，具有较好的应用价值。

关键字：消费者信用评估；分类；主成分分析；KS距离中图分类号：文章标志码：A1 引言近年来，，我国的消费信贷快速发展，2003年全国消费信贷余额为15790亿元，比1997增长了90倍，消费信贷占整个信贷的比例从不足0.3%上升到9.3%[1]。

但在消费信贷如火如荼的发展过程中，一些阻碍消费信贷的因素也越来越被人们所认识，如，消费信贷的门槛太高，审批的手续烦杂，审批时间过长等等。

金融界将诸多制约因素归因为个人信用体系的缺失,并见仁见智地提出了建立个人制度的种种设想与方案[2,3]。

但是，建立个人信用制度是一项非常复杂的系统工程，需要政府有关部门、金融机构、个人信用中介机构的密切合作，并非一日之功。

对于银行等授信机构来说，更为现实的问题是，如果能够在现有环境下，科学、高效地确定信用发放的对象，就能使自身的市场竞争力与效益得到巨大的提高。

而确定信用发放对象的过程，首先表现为对申请贷款消费者的信用评估方法是否高效、科学。

消费者信用评估的主要目的是对可能引起信用风险的因素进行定性分析、定量计算，以测量消费者的违约概率，为授信方决策提供依据。

目前信用评估最常用方法是“分类”方法——根据消费者的若干原始资料，通过若干方法，将其分为正常类(按期还本付息)和违约类，或给出一个违约概率或信用等级，，收稿日期：基金项目：中国科学院院长基金(yjjz946)、中国科学院科技政策与管理研究所所长基金(0343sz) 作者简介：（1976－），男（汉族），浙江建德人，中国科技大学商学院与中科院科技政策与管理科学研究所联合培养博士生，研究方向：风险管理与数据挖掘技术。