第2讲_CAE技术基本求解过程

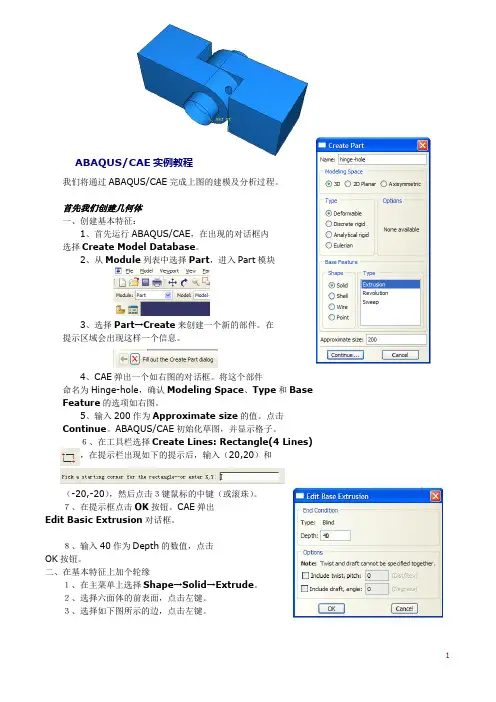
我们将通过ABAQUS/CAE完成上图的建模及分析过程。

首先我们创建几何体一、创建基本特征：1、首先运行ABAQUS/CAE，在出现的对话框内选择Create Model Database。

2、从Module列表中选择Part，进入Part模块3、选择Part→Create来创建一个新的部件。

在提示区域会出现这样一个信息。

4、CAE弹出一个如右图的对话框。

将这个部件命名为Hinge-hole，确认Modeling Space、Type和Base Feature的选项如右图。

5、输入200作为Approximate size的值。

点击Continue。

ABAQUS/CAE初始化草图，并显示格子。

６、在工具栏选择Create Lines: Rectangle(4 Lines)，在提示栏出现如下的提示后，输入（20,20）和７、在提示框点击OK按钮。

CAE弹出Edit Basic Extrusion对话框。

８、输入40作为Depth的数值，点击OK按钮。

二、在基本特征上加个轮缘１、在主菜单上选择Shape→Solid→Extrude。

２、选择六面体的前表面，点击左键。

３、选择如下图所示的边，点击左键。

４、如右上图那样利用图标创建三条线段。

５、在工具栏中选择Create Arc: Center and 2 Endpoints６、移动鼠标到(40,0.0)，圆心，点击左键，然后将鼠标移到(40,20)再次点击鼠标左键，从已画好区域的外面将鼠标移到(40,20)，这时你可以看到在这两个点之间出现一个半圆，点击左键完成这个半圆。

７、在工具栏选择Create Circle: Center and Perimeter８、将鼠标移动到(40,0.0)点击左键，然后将鼠标移动到(50,0.0)点击左键。

９、从主菜单选择Add→Dimension→Radial，为刚完成的圆标注尺寸。

10、选择工具栏的Edit Dimension Value图标11、选择圆的尺寸(10)点击左键，在提示栏输入12，按回车。

常问 CAE 界面操作前处理：1、如何显示梁截面（如何显示三维梁模型）a）无论是运算还是默认显示，ABA中的梁都是一条线,显示梁截面：view->assembly display option->render beam profiles/view->part display option->render beam profiles，自己调节系数。

b）后处理在deformed shape和undeformed shape都能用上面的方法显示梁截面，在应力云图（contour）不能显示。

c) Conventional shell 沒有辦法顯示厚度，因為本身就是用一代表面去表達實際幾何(一般常用中平面)。

但如果想觀察厚度方向的應力變化，可在後處理觀察(透過選擇fraction).而continuum shell可以顯示厚度，因其是以實際幾何去表達如需考慮厚度的改變，使用continuum shell會更容易釐清問題。

更詳細內容可參考Abaqus Analysis User's Manual 24.6節Shell elements。

2、4 建立几何模型草绘sketch的时候，发现画布尺寸太小了1）这个在create part的时候就有approximate size，你可以定义合适的（比你的定性尺寸大一倍）；如果你已经在sketch了，可以在edit菜单－－sketch option －－grid更改2）这里如果你选择constriant标签，还能更改尺寸精度3、如何定义局部坐标系Tool－Create Datum－CSYS－－建立坐标系方式－－选择直角坐标系or柱坐标系or球坐标4、如何在局部坐标系定义载荷laod－－Edit load－－CSYS－Edit（在BC中同理）选用你定义的局部坐标系5、怎么知道模型单元数目（一共有多少个单元）在mesh步，mesh verify 可以查到单元类型，数目以及单元质量一目了然，Query---element 也可以查询的。

CAE的基本原理1）粘性流體力學的基本方程(1) 廣義牛頓定律，反映了一般工程問題範圍內粘性流體的應力張量與應變速率張量之間的關係，數學運算式為本構方程。

(2) 品質守恆定律，其含義是流體的品質在運動過程中保持不變，數學運算式為連續性方程。

(3) 動量守恆定律，其含義是流體動量的時間變化率等於作用於其上的外力總和，數學運算式為運動方程。

(4) 熱力學第一定律，其含義是系統內能的增加等於對該系統所作的功與加給該系統的能量之和，數學運算式為能量方程。

2）塑膠熔體充模流動的簡化和假設(1) 由於型腔壁厚(z向)尺寸遠小於其他兩個方向(x和y方向)的尺寸且塑膠熔體粘性較大，所以熔體的充模流動可視為擴展層流，z向的速度分量可忽略不計，且認為壓力不沿z向變化。

(2) 充模過程中熔體壓力不是很高，因此可視熔體為未壓縮流體。

(3) 由於熔體粘性較大，相對于粘性剪切應力而言，慣性力和品質力都很小，可忽略不計。

(4) 在熔體流動方向(x和y方向)上，相對于熱對流項而言，熱傳導項很小，可忽略不計。

(5) 熔體不含內熱源。

(6) 在充模過程中，熔體溫度變化不大，可認為比熱容和導熱係數是常數。

(7) 熔體前沿採用平面流前模型。

3）塑膠熔體充模流動的控制方程5）數值計算實施過程與策略CAE軟體的應用過程。

首先根據製品的幾何模型剖分具有一定厚度的三角形單元，對各三角形單元在厚度方向上進行有限差分網格剖分，在此基礎上，根據熔體流動控制方程在中性層三角形網格上建立節點壓力與流量之間的關係，得到一組以各節點壓力為變數的有限元方程，解方程組求得節點壓力分佈，同時將能量方程離散到有限元網格和有限差分網格上，建立以各節點在各差分層對應位置的溫度為未知量的方程組，求解方程組得到節點溫度在中性層上的分佈及其在厚度方向上的變化，由於壓力與溫度通過熔體粘度互相影響，因此必頇將壓力場與溫度場進行迭代耦注射溫度熔體流入冷卻的型腔，因熱傳導而散失熱量。

Abaqus_CAE基础培训实例教程我们将通过ABAQUS/CAE完成上图的建模及分析过程。

首先我们创建几何体一、创建基本特征：1、首先运行ABAQUS/CAE，在出现的对话框内选择Create Model Database。

2、从Module列表中选择Part，进入Part模块3、选择Part→Create来创建一个新的部件。

在提示区域会出现这样一个信息。

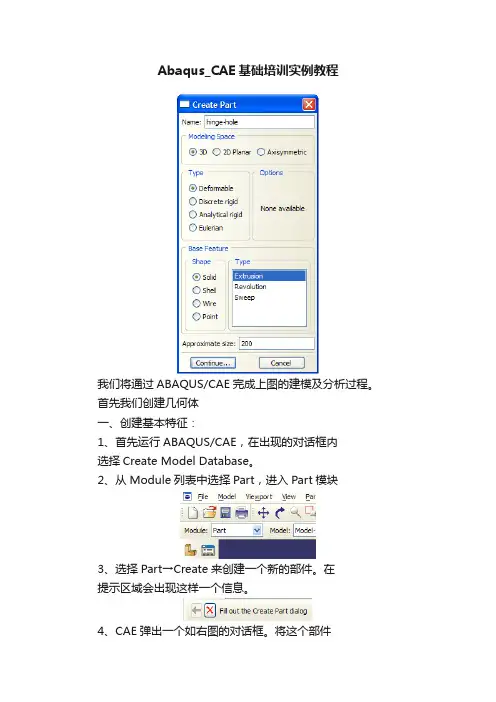
4、CAE弹出一个如右图的对话框。

将这个部件命名为Hinge-hole，确认Modeling Space、Type和Base Feature的选项如右图。

5、输入200作为Approximate size的值。

点击Continue。

ABAQUS/CAE初始化草图，并显示格子。

６、在工具栏选择Create Lines: Rectangle(4 Lines)，在提示栏出现如下的提示后，输入（20,20）和７、在提示框点击OK按钮。

CAE弹出Edit Basic Extrusion对话框。

８、输入40作为Depth的数值，点击OK按钮。

二、在基本特征上加个轮缘１、在主菜单上选择Shape→Solid→Extrude。

２、选择六面体的前表面，点击左键。

３、选择如下图所示的边，点击左键。

４、如右上图那样利用图标创建三条线段。

５、在工具栏中选择Create Arc: Center and 2 Endpoints６、移动鼠标到(40,0.0)，圆心，点击左键，然后将鼠标移到(40,20)再次点击鼠标左键，从已画好区域的外面将鼠标移到(40,20)，这时你可以看到在这两个点之间出现一个半圆，点击左键完成这个半圆。

７、在工具栏选择Create Circle: Center and Perimeter８、将鼠标移动到(40,0.0)点击左键，然后将鼠标移动到(50,0.0)点击左键。

９、从主菜单选择Add→Dimension→Radial，为刚完成的圆标注尺寸。

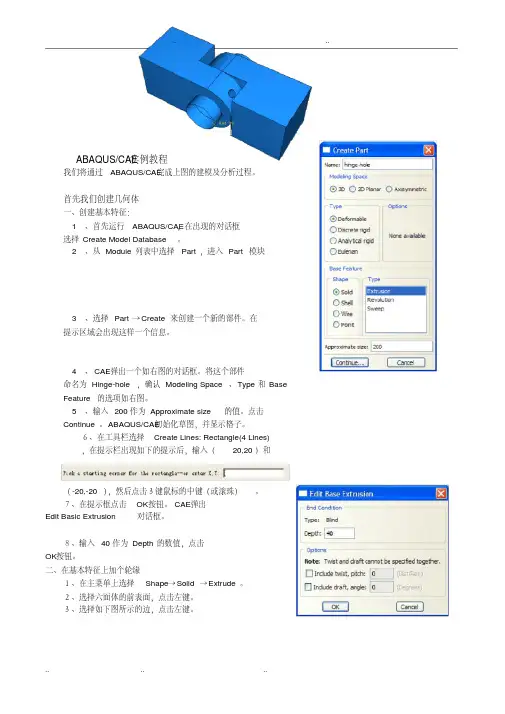
ABAQUS/CAE实例教程我们将通过ABAQUS/CAE完成上图的建模及分析过程。

首先我们创建几何体一、创建基本特征：1、首先运行ABAQUS/CAE，在出现的对话框选择Create Model Database。

2、从Module列表中选择Part，进入Part模块3、选择Part→Create来创建一个新的部件。

在提示区域会出现这样一个信息。

4、CAE弹出一个如右图的对话框。

将这个部件命名为Hinge-hole，确认Modeling Space、Type和Base Feature的选项如右图。

5、输入200作为Approximate size的值。

点击Continue。

ABAQUS/CAE初始化草图，并显示格子。

６、在工具栏选择Create Lines: Rectangle(4 Lines)，在提示栏出现如下的提示后，输入（20,20）和（-20,-20），然后点击３键鼠标的中键（或滚珠）。

７、在提示框点击OK按钮。

CAE弹出Edit Basic Extrusion对话框。

８、输入40作为Depth的数值，点击OK按钮。

二、在基本特征上加个轮缘１、在主菜单上选择Shape→Solid→Extrude。

２、选择六面体的前表面，点击左键。

３、选择如下图所示的边，点击左键。

４、如右上图那样利用图标创建三条线段。

５、在工具栏中选择Create Arc: Center and 2 Endpoints６、移动鼠标到(40,0.0)，圆心，点击左键，然后将鼠标移到(40,20)再次点击鼠标左键，从已画好区域的外面将鼠标移到(40,20)，这时你可以看到在这两个点之间出现一个半圆，点击左键完成这个半圆。

７、在工具栏选择Create Circle: Center and Perimeter８、将鼠标移动到(40,0.0)点击左键，然后将鼠标移动到(50,0.0)点击左键。

９、从主菜单选择Add→Dimension→Radial，为刚完成的圆标注尺寸。

铸造cae基本流程
铸造CAE基本流程
铸造过程的仿真分析是整个产品开发周期中一个非常重要的环节,通过有限元分析软件可以预测铸件的充型、固化及缩孔缺陷等质量问题,并优化工艺参数。

下面是铸造CAE基本流程:
1. 建立三维模型
根据产品图纸,使用三维建模软件如Pro/E、SolidWorks等建立铸件三维实体模型和各类型浇口系统模型。

2. 网格划分
将模型导入有限元前处理模块,为模型划分网格,其中对于重点区域可以加密网格。

合理的网格划分对仿真精度至关重要。

3. 设置边界条件和材料参数
设置铸造工艺参数,如浇注温度、金属材料物性、浇注系统参数等。

同时也需设置模具壁面传热参数。

4. 计算分析
使用有限元求解器进行数值计算分析,包括模拟金属液流动、固液共存和完全固化等物理过程。

5. 后处理
利用后处理模块查看计算结果,如充型过程、温度场、残余应力场、
缩孔预测等。

根据结果诊断铸件质量问题。

6. 优化设计
根据仿真结果修改浇注系统、调整工艺参数,然后重复上述步骤,直至获得满意的优化方案。

通过上述流程,可以大大缩短新产品开发周期,减少实际试制成本,提高铸件质量和工艺成熟度,实现精益生产。

1. 有限元分析概述对于一般的工程受力问题，希望通过平衡微分方程、变形协调方程、几何方程和本构方程联立求解而获得整个问题的精确解是十分困难的，一般几乎是不可能的。

随着20世纪五六十年代计算机技术的出现和发展、以及工程实践中对数值分析要求的日益增长，并发展起来了有限元的分析方法。

有限元法自1960年由Clough首次提出后，获得了迅速的发展；虽然首先只是应用于结构的应力分析，但很快就广泛应用于求解热传导、电磁场、流体力学、成形工艺等连续问题。

1.1、有限元法的基本概念对于连续体的受力问题，既然作为一个整体获得精确求解十分困难；于是，作为近似求解，可以假想地将整个求解区域离散化，分解成为一定形状有限数量的小区域（即单元），彼此之间只在一定数量的指定点（即节点）处相互连接，组成一个单元的集合体以替代原来的连续体，如图7-1弯曲凹模的受力分析所示；只要先求得各节点的位移，即能根据相应的数值方法近似求得区域内的其他各场量的分布；这就是有限元法的基本思想。

从物理的角度理解，即将一个连续的凹模截面分割成图7-1所示的有限数量的小三角形单元，而单元之间只在节点处以铰链相连接，由单元组合成的结构近似代替原来的连续结构。

如果能合理地求得各单元的力学特性，也就可以求出组合结构的力学特性。

于是，该结构在一定的约束条件下，在给定的载荷作用下，各节点的位移即可以求得，进而求出单元内的其他物理场量。

这就是有限元方法直观的物理的解释。

从数学角度理解，是将图7-1所示的求解区域剖分成许多三角形子区域，子域内的位移可以由相应各节点的待定位移合理插值来表示。

根据原问题的控制方程（如最小势能原理）和约束条件，可以求解出各节点的待定位移，进而求得其他场量。

推广到其他连续域问题，节点未知量也可以是压力、温度、速度等物理量。

这就是有限元方法的数学解释。

从有限元法的解释可得，有限元法的实质就是将一个无限的连续体，理想化为有限个单元的组合体，使复杂问题简化为适合于数值解法的结构型问题；且在一定的条件下，问题简化后求得的近似解能够趋近于真实解。