高数第九章(10)最小二乘法

最小二乘法基本原理：成对等精度测得一组数据，试找出一条最佳的拟合曲线，使得这条曲线上的各点值与测量值的平方和在所有的曲线中最小。

我们用最小二乘法拟合三次多项式。

最小二乘法又称曲线拟合，所谓的“拟合”就是不要求曲线完全通过所有的数据点，只要求所得的曲线反映数据的基本趋势。

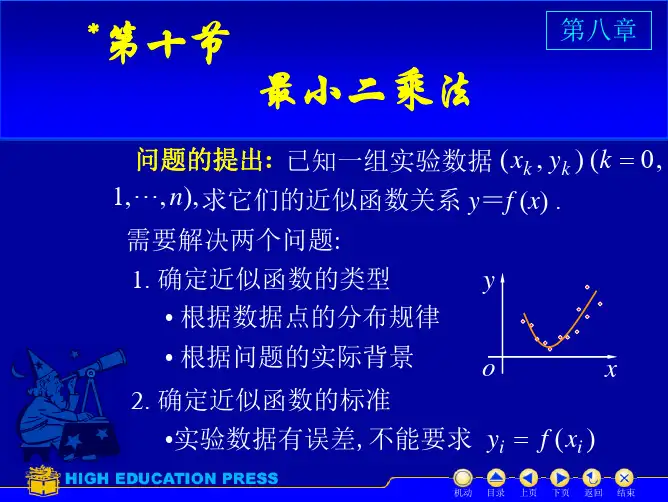
曲线的拟合几何解释：求一条曲线，使所有的数据均在离曲线的上下不远处。

第一节 最小二乘法的基本原理和多项式拟合 一最小二乘法的基本原理从整体上考虑近似函数)(x p 同所给数据点),(i i y x (i=0,1,…,m)误差i i i y x p r -=)((i=0,1,…,m)常用的方法有以下三种：一是误差i i i y x p r -=)((i=0,1,…,m)绝对值的最大值im i r ≤≤0max ，即误差 向量T m r r r r ),,(10 =的∞—范数；二是误差绝对值的和∑=mi ir 0，即误差向量r 的1—范数；三是误差平方和∑=mi ir02的算术平方根，即误差向量r 的2—范数；前两种方法简单、自然，但不便于微分运算 ，后一种方法相当于考虑 2—范数的平方，因此在曲线拟合中常采用误差平方和∑=mi ir02来 度量误差i r (i=0，1，…，m)的整体大小。

数据拟合的具体作法是：对给定数据 ),(i i y x (i=0,1,…，m)，在取定的函数类Φ中,求Φ∈)(x p ,使误差i i i y x p r -=)((i=0,1,…,m)的平方和最小，即∑=m i ir 02=[]∑==-mi ii y x p 02min)(从几何意义上讲，就是寻求与给定点),(i i y x (i=0,1,…,m)的距离平方和为最小的曲线)(x p y =（图6-1）。

函数)(x p 称为拟合 函数或最小二乘解，求拟合函数)(x p 的方法称为曲线拟合的最小二乘法。

Φ可有不同的选取方法.6—1二多项式拟合假设给定数据点),(i i y x (i=0,1,…,m)，Φ为所有次数不超过)(m n n ≤的多项式构成的函数类，现求一Φ∈=∑=nk k k n x a x p 0)(,使得[]min )(00202=⎪⎭⎫⎝⎛-=-=∑∑∑===mi mi n k i k i k i i n y x a y x p I (1)当拟合函数为多项式时，称为多项式拟合，满足式（1）的)(x p n 称为最小二乘拟合多项式。

高中数学最小二乘法最小二乘法是一种常用的统计学方法，通常应用于数据拟合。

在高中数学中，最小二乘法主要用于线性回归分析，即寻找一条直线来拟合一组数据点。

假设有一组数据 $(x_1,y_1),(x_2,y_2),cdots,(x_n,y_n)$，我们希望找到一条直线 $y = ax + b$，使得这条直线与这些数据点的误差平方和最小。

换句话说，就是让这条直线尽可能地接近这些数据点。

假设直线 $y = ax + b$ 与数据点 $(x_i,y_i)$ 的误差为 $e_i$，则有：$$e_i = y_i - (ax_i + b)$$将所有数据点的误差平方和表示出来，可以得到：$$sum_{i=1}^n e_i^2 = sum_{i=1}^n(y_i - (ax_i + b))^2$$ 我们的目标是使得上式的值最小，因此需要对 $a$ 和 $b$ 分别求偏导数并令其为0，得到：$$begin{cases}frac{partial}{partial a}sum_{i=1}^n e_i^2 = 0 frac{partial}{partial b}sum_{i=1}^n e_i^2 = 0end{cases}$$ 将上式展开并整理可得到：$$begin{cases}displaystylesum_{i=1}^n x_i(y_i - ax_i - b) = 0displaystylesum_{i=1}^n(y_i - ax_i - b) = 0end{cases}$$ 解出 $a$ 和 $b$ 即可得到最小二乘法的结果，即：$$a = frac{displaystyle nsum_{i=1}^nx_iy_i -sum_{i=1}^nx_isum_{i=1}^ny_i}{displaystyle nsum_{i=1}^nx_i^2 - (sum_{i=1}^nx_i)^2}$$$$b = frac{displaystyle sum_{i=1}^ny_i - asum_{i=1}^nx_i}{n}$$这就是高中数学中最小二乘法的基本原理和公式。

2015考研数学基础阶段学习计划（数二）考研数学一般考察考生的基础知识的掌握和运用解题的能力。

数学的复习需要一步一步的积累知识、循序渐进地完全掌握。

学好考研数学，务必要夯实基础。

在此，建议您在6月底之前前完成基础阶段的学习，3月份之前主要是以教材、零基础入门课程为主，把教材上的习题做一遍，然后3月份——6月份把基础课程学习一遍，以便于后面的强化、冲刺。

根据考研数学中高数、线代所占分值的不同，对不同章节确定了合理的学习时间。

复习计划使用说明：(1) 计划里明确了每章节的重难点，以及不需要掌握的内容也已经指明，后面备有考纲规定的考试内容，同学们要根据大纲要求合理学习知识点。

(2) 同学们在学习的时候如果有条件一定要和你周围的同学、老师多交流学习心得。

只有你总结出来的方法才是最适合你的方法。

(3) 同学们在学习的过程中难免会遇到一些疑难问题、做错的题目，一定要在第一时间把它整理到你的笔记本里，并到名师堂提问。

本阶段主要复习资料是大学教材，包括高等数学、线性代数，如果手头没有这几本书，推荐购买：《高等数学》同济第六版上下册；《工程数学线性代数》同济第五版。

学习课程：高等数学零基础入门（一元函数微积分学）、线性代数零基础入门（线代基础）高等数学基础、线性代数基础说明：听课之前一定要复习过一遍教材，这样在听课的时候才能抓住重点。

零基础入门课程所讲内容是考研数学最基础，也是最重要的部分，其中包括了与考研数学紧密联系的部分高中知识，如三角函数等。

数学的学习是一个循序渐进、由浅入深的过程，夯实基础尤为关键，之后的学习才能达到事半功倍的效果。

建议先学习零基础入门课程，然后再学习基础课程。

学习顺序：教材与零基础入门课程同步进行，之后学习基础课程。

复习教材的时候先复习高等数学内容，高等数学是基础，然后再复习线性代数。

过完一轮教材之后跟着我们的课程再学习一遍。

注意：预习内容时，请参考考试大纲的考试内容（最后一列）预习。

考试大纲不要的章节内容不用看。

最小二乘法1：最小二乘法的原理与要解决的问题最小二乘法是由勒让德在19世纪发现的，形式如下式：标函数 = \sum（观测值-理论值）^2\\观测值就是我们的多组样本，理论值就是我们的假设拟合函数。

目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使目标函数最小化时候的拟合函数的模型。

举一个最简单的线性回归的简单例子，比如我们有 m 个只有一个特征的样本： (x_i, y_i)(i=1, 2, 3...,m)样本采用一般的 h_{\theta}(x) 为 n 次的多项式拟合，h_{\theta}(x)=\theta_0+\theta_1x+\theta_2x^2+...\theta _nx^n,\theta(\theta_0,\theta_1,\theta_2,...,\theta_n) 为参数最小二乘法就是要找到一组\theta(\theta_0,\theta_1,\theta_2,...,\theta_n) 使得\sum_{i=1}^n(h_{\theta}(x_i)-y_i)^2 (残差平方和) 最小，即，求 min\sum_{i=1}^n(h_{\theta}(x_i)-y_i)^22 ：最小二乘法的矩阵法解法最小二乘法的代数法解法就是对 \theta_i 求偏导数，令偏导数为0，再解方程组，得到 \theta_i 。

矩阵法比代数法要简洁，下面主要讲解下矩阵法解法，这里用多元线性回归例子来描：假设函数h_{\theta}(x_1,x_2,...x_n)=\theta_0+\theta_1x_1+...+\t heta_nx_n 的矩阵表达方式为：h_{\theta}(\mathbf{x})=\mathbf{X}\theta\\其中，假设函数 h_{\theta}(\mathbf{x})=\mathbf{X}\theta 为 m\times1 的向量, \theta 为 n\times1 的向量，里面有 n 个代数法的模型参数。

最小二乘法概述最小二乘法是一种常用的回归分析方法，用于拟合一个模型到实际观测数据中。

最小二乘法的目标是最小化观测数据的残差平方和，从而找到最佳拟合曲线或者面。

原理给定一组实际观测数据点(X, Y)，我们的目标是找到一个函数 y=f(x) 使其能够拟合这些数据点。

最小二乘法的基本原理是使模型的预测值与实际观测值之间的残差平方和最小化。

最小二乘法的基本假设是，观测数据点之间的误差是独立同分布的，并且服从正态分布。

这意味着观测数据点具有相同的误差方差，并且误差服从一个以零为均值的正态分布。

最小二乘法使用了一个常见的线性模型，其中函数 f(x) 是一个线性组合参数向量β 和自变量向量 X 的乘积。

即y = β0 + β1*x1 +β2*x2 + ... + βn*xn。

在拟合过程中，需要找到最佳的参数向量β，使得拟合的模型能够最好地描述数据。

最小二乘法求解过程可以通过多种方法实现，其中最常用的是正规方程法，该方法通过求解一个线性方程组来得到最佳参数向量β。

另外，还可以使用梯度下降法等迭代方法来求解。

应用最小二乘法在实际问题中有广泛的应用。

以下是一些常见的应用领域：1. 经济学：最小二乘法可用于拟合经济模型，例如线性需求模型和生产函数模型。

这些模型可以用于预测和解释经济现象。

2. 金融学：最小二乘法可用于拟合股票价格、利率曲线和其他金融数据。

这样的模型可以用于金融风险管理和投资决策。

3. 物理学：最小二乘法在物理学中也有广泛的应用，例如拟合实验数据以确定物理模型的参数，或者拟合传感器数据以估计物理量。

4. 工程学：最小二乘法可用于工程领域的多个应用，例如信号处理、图像处理和控制系统设计。

5. 人工智能：最小二乘法在机器学习和数据挖掘领域也有应用。

例如，在线性回归和支持向量机等算法中，最小二乘法可以用于模型参数的拟合。

优势和局限性最小二乘法的主要优势是简单直观，易于理解和实现。

它提供了一种有效的方法来拟合数据并得到参数的估计。

一文让你彻底搞懂最小二乘法（超详细推导）要解决的问题在工程应用中，我们经常会用一组观测数据去估计模型的参数，模型是我们根据先验知识定下的。

比如我们有一组观测数据 ( x i , y i ) (x_i,y_i) (xi,yi)（一维），通过一些数据分析我们猜测 y y y和 x x x之间存在线性关系，那么我们的模型就可以定为： f ( x ) = k x + b f(x)=kx+bf(x)=kx+b这个模型只有两个参数，所以理论上，我们只需要观测两组数据建立两个方程，即可解出两个未知数。

类似的，假如模型有n n n个参数，我们只需要观测 n n n组数据就可求出参数，换句话说，在这种情况下，模型的参数是唯一确定解。

但是在实际应用中，由于我们的观测会存在误差（偶然误差、系统误差等），所以我们总会做多余观测。

比如在上述例子中，尽管只有两个参数，但是我们可能会观测 n n n组数据( x 1 , y 1 ) . . , ( x n , y n ) (x_1, y_1)..,(x_n, y_n) (x1,y1)..,(xn,yn)，这会导致我们无法找到一条直线经过所有的点，也就是说，方程无确定解。

于是这就是我们要解决的问题：虽然没有确定解，但是我们能不能求出近似解，使得模型能在各个观测点上达到“最佳“拟合。

那么“最佳”的准则是什么？可以是所有观测点到直线的距离和最小，也可以是所有观测点到直线的误差（真实值-理论值）绝对值和最小，也可以是其它，如果是你面临这个问题你会怎么做？早在19世纪，勒让德就认为让“误差的平方和最小”估计出来的模型是最接近真实情形的。

为什么是误差平方而不是另一个？就连欧拉和拉普拉斯都没能成功回答这个问题。

后来高斯建立了一套误差分析理论，从而证明了系统在误差平方和最小的条件下是最优的。

证明这个理论并不难。

我写了另一篇关于最小二乘法原理理解的博客。

相信你了解后会对最小二乘法有更深的理解。

最小二乘法最小二乘法（Least Squares Method）是一种统计学上常用的参数估计方法，通过最小化观测数据与理论模型之间的误差的平方和，来估计模型的参数。

在统计学和数学中，最小二乘法被广泛应用于曲线拟合、回归分析、数据处理以及信号处理等领域。

最小二乘法的基本思想是，通过找到可以使得各观测数据与理论模型预测的数据之间的差异最小的参数估计值，从而得到最佳的拟合结果。

它是一种数学上比较成熟且有效的方法，可以用来解决具有一定误差的线性和非线性函数拟合问题。

在应用最小二乘法时，首先需要建立数学模型来描述观测数据与自变量之间的关系。

这个数学模型可以是线性的，也可以是非线性的，根据实际问题的特点来确定。

然后，根据观测数据和数学模型，利用最小二乘法的原理来求解模型的参数估计值。

最小二乘法的基本步骤如下：1. 建立数学模型：通过分析问题的背景和要求，确定观测数据与自变量之间的关系，并建立数学模型。

2. 确定误差函数：定义误差函数，它是观测数据与数学模型之间的差异度量。

3. 最小化误差函数：通过最小化误差函数，即求解误差函数的导数为0的参数估计值，来得到最佳的模型拟合结果。

4. 评估拟合结果：通过各种统计指标和图示分析来评估最小二乘拟合的效果，并对结果进行解释和验证。

最小二乘法的优点在于它是一种数学上比较简单和直观的方法，并且在实际应用中得到了广泛的应用。

它能够充分考虑观测数据的误差，通过最小化误差的平方和来估计模型的参数，从而得到较为可靠的拟合结果。

最小二乘法的应用非常广泛，涵盖了许多学科领域，如物理学、经济学、工程学、生物学和地球科学等。

在曲线拟合中，最小二乘法可以用来拟合直线、曲线和曲面等；在回归分析中，最小二乘法可以用来建立回归模型，并进行参数估计和显著性检验；在数据处理中，最小二乘法可以用来进行信号滤波和数据平滑等。

总之，最小二乘法是一种重要的数学和统计方法，在许多实际问题中起着重要的作用。

它不仅可以用来拟合曲线和回归分析，还可以应用于信号处理、数据处理和参数估计等领域。

最小二乘法通俗讲解方法说白了，最小二乘法就是帮助我们找到一条直线，尽可能靠近一堆散落的点。

就像你在超市买水果，想挑选最成熟的苹果，但总是有些苹果看起来有点皱，那就得靠近一些，更挑剔一些，才能挑到最好。

数据点就是这些苹果，而那条直线就是你挑出来的“最佳选择”。

可别小看这条线，它能告诉你很多东西，比如说未来的趋势，或者某种关系的强弱。

怎么找到这条神奇的直线呢？很简单，咱们先给这些点打个分。

也就是说，咱们看每个点和这条线之间的距离，越近越好，离得远的就像你和你的初恋一样，遥不可及。

最小二乘法就是用这种方式，把每个点和直线之间的距离的平方相加，求一个最小值。

这听起来有点复杂，但实际上就是把这些“错误”加起来，尽量让它们的小脾气消失。

这样做的好处是什么呢？想象一下，你在做一个拼图，每一块都得合在一起才能形成一幅美丽的画。

最小二乘法帮助我们找到这些拼图块的完美位置，最终拼出一幅完整的图景。

就好比，你要用数据预测明天的天气，找到趋势，掌握风向，才能不被突如其来的雨淋个透心凉。

用这个方法还可以解决很多实际问题。

比如，想知道学习时间和考试成绩的关系，或者你每天的跑步距离和体重变化之间的联系。

就像你去健身房，想知道做多少次深蹲才能瘦下来，这些数据能够帮助你找到最佳的训练方案。

最小二乘法让这些关系变得清晰可见，不再是一团迷雾。

最小二乘法也不是完美的，它有时会受到一些异常值的影响。

这就好比你在群聊里发了一条消息，结果被某个不合群的小伙伴抢了风头，搞得大家都没法集中注意力。

不过，咱们可以通过一些技术手段，比如加权最小二乘法，来处理这些问题，保证我们的分析结果更靠谱。

最小二乘法就像是我们生活中的导航仪，帮我们在数据的海洋中找到方向。

它简单易懂，却能解决很多复杂的问题。

在这个快速变化的时代，掌握这样的方法，绝对能让你在职场和生活中如鱼得水，顺风顺水。

所以，下次你听到“最小二乘法”这几个字，不妨轻松一下，想象一下它就是你生活中的小助手，帮助你理清思路，找到最优解。

多维最小二乘法
多维最小二乘法是一种优化方法，通过最小化误差的平方和寻找数据的最佳函数匹配，从而求解过度定参数模型。

假设拟合函数为$y=f(x;θ)$，$θ$为未知参数，$y$为观测值，$x$为样本，$m$为样本数，则目标函数（loss function）为：$\sum_{i=1}^{m}(y_i-f(x_i;θ))^2$。

在多维空间中，线性是一个超平面，最小二乘法实际是寻找向量间最佳的线性组合，使得其与目标向量的差最小。

在向量张成的空间中找到与目标向量残差最小的向量，该向量与目标向量的差即为残差，当目标向量在向量张成的空间的投影最大时残差最小，此时残差与空间垂直。

多维最小二乘法在样本量较大时，能够获得较为准确的统计参数估计，具有线性和非偏性的特点，并且易于理解和实现。