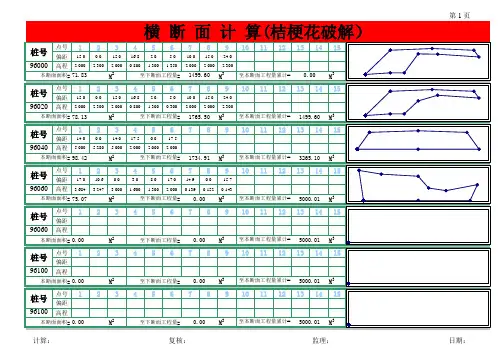
横断面计算程序

任务4 路基土石方计算与调配在公路工程项目中，路基土石方数量十分可观，它是公路工程项目的一项主要指标，直接影响公路建设的造价、工期、用地等许多方面。

土石方的数量及其调配，关系着取土或弃土地点、公路用地范围，同时对工程造价、所需劳动力和机具设备的数量以及施工期限有较大影响。

土石方数据计算与调配的主要任务是计算每公里路段的土石方数量和全线总土石方工程数量，合理调配挖方的利用和填方的来源及运距，为编制工程预（概）算、确定合理的施工方案以及计量支付提供依据。

由于自然地面起伏多变，填挖体积不可能是一个简单的几何体，若按地面的起伏变化来进行土石方数量的计算，不仅繁杂，而且实用意义不大。

因此，在公路的测设过程中，土石方的计算通常采用近似方法，计算精度视工程的要求而定。

一般情况下，横断面的面积以m2为单位，可取小数后一位，土石方的体积以m3为单位，可取至整数。

一、横断面面积计算路基填挖的断面积是指断面图中地面线与路基设计线所围成的面积，包括填方区域面积与挖方区域面积，在断面面积计算时，填方与挖方应分别考虑。

常用的断面面积计算方法有积距法、坐标法、几何图形法和混合法。

1、积距法积距法的原理是把断面面积垂直分割成宽度相等的若干条块，由于每一条块的宽度相等，所以在计算面积时，只需量取每一条块的平均高度，然后乘以宽度，即可得出每一条块的面积，如图3-12所示。

其计算公式为：（3-1）式中：——横断面面积，；——横断面所分成的三角形或梯形条块的宽度，通常用1m或2m；——横断面所分成的三角形或梯形条块的平均高度，m。

图3-12 积距法计算示意图图3-13 坐标法由此可见，积距法求面积就是在实际操作中转化为量取的累加值，这种操作可以使用分规按顺序由左到右连续量取每一条块的平均高度，分规最后的累计高就是，将条块宽度乘以累计高度即为填或挖的面积。

积距法也可以用厘米格纸拆成窄条作为量尺，每量一次在窄条上画好标记，从开始到最后标记的累计距离就是，然后乘以条块宽度即为所求面积。

8
0.0 0.152
9
-15.7 0.143
10
11
12
13
14
15
本断面面积= 75.07
M2
至下断面工程量=
0.00
M3
至本断面工程量累计=
5000.01
M3
桩号
96060
点号 偏距 高程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
本断面面积= 0.00
M
2
至下断面工程量=
0.00
M
3
至本断面工程量累计=
14
15
本断面面积= 0.00
M
2
至下断面工程量=
0.00
M
3
至本断面工程量累计=
5000.01
M
3
桩号
点号 偏距 高程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
本断面面积= 0.00
M
2
至下断面工程量=
0.00
M
3
至本断面工程量累计=
5000.01
M
3
桩号
点号 偏距 高程
1
2
3
4
5
6
7
8
9
10
11
M
3
桩号
点号 偏距 高程
1
2
3
4
5
6
7
8
9
10
11

5.6 横断面设计方法及成果
5.6.1 横断面设计步骤
1. 公路横断面设计内容
（1）确定路幅横断面尺寸（宽度及横坡度）； （2）确定路基高度：纵断面设计完成； （3）路基横断面形状设计：直线式边坡
折线式边坡 台阶形边坡； （4）边坡坡度确定；路堤及路堑边坡 土质与岩石边坡 （5）绘制横断面图； （6）横断面面积计算及土石方数量计算与调配。
1．在计算纸上绘制横断面的地面线。 地面线是在现场测绘的，若是纸上定线，可从大比例尺的地形图上内
插获得。 横断面图的比例尺一般是1：200。
2．绘出设计线：“戴帽子”
3. 绘出路基防护及加固设施的断面图。 4．绘出路基排水设施的断面图。 ➢ 根据综合排水设计，画出路基边沟、截水沟、排灌渠等的位置和 断面形式。
1. 土石方调配原则 ▪ （1）就近利用，以减少运量； ▪ （2）不跨沟调运； ▪ （3）高向低调运； ▪ （4）经济合理； ▪ 应进行远运利用与附近借土的经济比较（移挖作填与借土费用的
比较）。 ▪ 远运利用的费用：运输费用、装卸费等 ▪ 借土费用：开挖费用、占地及青苗补偿费用、弃土占地及运费 ▪ （5）不同的土方和石方应根据工程需要分别进行调配，以保证路基
A2 )L
A2
A1
5.7.2 土石方数量计算
1. 平均断面法： 若相邻两断面均为填方或均为挖方且面积大小相近，则可假定两断
面之间为一棱柱体其体积的计算公式为：
1 V 2 ( A1 A2 )L
2. 棱台体积法： 若A1和A2相差甚大，则与棱台更为接近。其计算公式为：
1 V 3 ( A1 A2 A1A2 )L
5.7.3 路基土石方调配
▪ 土石方调配的目的：确定填方用土的来源、挖方弃土的去向；以及计价 土石方的数量和运量等。

积距法计算迅速、操作简便，是目前广泛采用的方法，因常用“分规” 来卡得积距值，又称卡规法。如图所示，先将所计算面积分成横距为L的 则总面积为各条块面积累加之和，即 A Ai h1l h2l hnl l hi
在实用中，为避免“分规”的松动而影响计算准确和“分规”脚尖刺破 图纸，可用毫米方格纸折成窄条作为量尺，代替“分规”量取积距，并 可随即读得所计算的填、挖面积。
2 块分法
块分法是把横断面图上地面线及设计线的转折点，划分成若干块不等 宽的梯形或三角形，分别计算每一块图形的面积，并累加起来，即为 该横截面的面积。块分法适用于计算机计算，精度较高。
3 坐标法
坐标法是已知断面图上各转折点坐标（xi，yi），则断面面积计算为：
路基横断面面积计算
01
02
路基 横断面
03
模块四
路基横断面组成分析
路基横断面设计 路基横断面
面积计算
路基土石方数量计算及调配
路基横断面设计成果
C目 录 ONTENTS 1 积距法（条分法） 2 块分法 3 坐标法
1 积距法（条分法）
积距法是把横断面图划分成若干条等宽的小条，累加每一小条中心处的 高度，再乘以条宽即为该图形的面积。 积距法适用于不规则图形面积计算。

平均断面 面 积
距
体
积 m3
m
72.05 72.43 72.40 72.30 72.25 72.20 72.15 72.10 72.00
挖
0 2.01
填
8.32 3.48
m2 离 m 挖
1.01 1.80 0.79 0 0 0.63 1.18 1.21 70 30 100 50 50 50 50 100
3
1
2′
3′
1′
2
⑵测设过程如下 ① 将方向架立在 ZY点位，以方向架 1 − 1′方向对准
交点 JD 。转动杆 3 − 3′对准 p 点
1
1′
3′
将其拧紧固定。
2
JD
p3 p2 p1
ZY
p4
3
2′
1
将方向架移动到p 点。 ② 用方向架2 − 2′对准ZY点，（根据同一弧段弦 切角 相等的原理） 定向杆3 − 3′所指的方向 2′ 1 即为p 点处的横断方向。 3 JD
2.653
74.826 74.826
1.985
1.424 1.103
74.562 74.562 74.224 74.224
1.688 1.441 1.087
已知
8.416
7.402
∑h测=∑a-∑b=8.416－ ∑h测=∑a-∑b=8.416－7.402=1.014 fh=∑h测－（H终－ H始）=1.014－(73.140－72.123)=-0.003m =∑h测－（H =1.014－(73.140－72.123)=f h 允 = ± 40 L = ± 28 mm
检 计 核 算
1.123 2.113
73.246 73.246 74.158 74.158 1.201 0.98 1.25

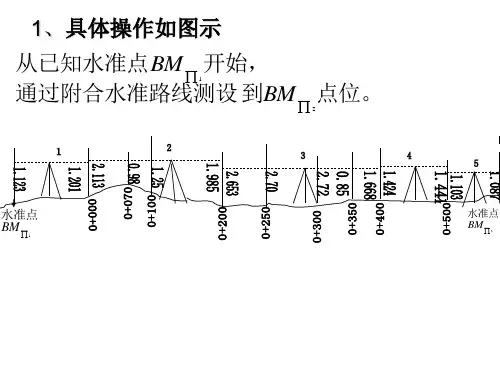
§5 渠道纵横断面设计简要解释“渠道纵横断面设计”横断面设计：确定渠道边坡、底宽、水深等。

纵断面设计：确定推算水位、确定渠底线、堤顶高程线等。

一、渠道横断面设计（一）基本公式明渠均匀流公式对于梯形断面渠道:（二）横断面计算方法１．计算底宽ｂ和设计水深ｈ优点：比试算法简便，比图解法精度更高。

２．计算加大水深和最小水深一般需2~3次迭代即可得到满意的结果。

（三）设计参数的确定１．渠底比降ｉ指单位渠长的渠底降落值。

当Q一定时, i大, 则过水断面A小,工程量小, 但控制的灌溉面积小。

i小, 则A大, 工程量大, 但控制的灌溉面大。

取值方法：（１）接近地面比降（２）Ｑ大，则ｉ宜小（防冲剧）（３）平原地区ｉ小，山丘区ｉ大２．渠床糙率ｎ反映渠床粗糙程度。

糙率大，则阻水能力大。

取值：（１）渠床光滑顺直，ｎ小（２）Ｑ大，则ｎ小参考教材表４-8。

请同学思考：ｎ取值偏大会造成什么后果？ｎ取值偏小会造成什么后果？３．边坡系数ｍm大, 则工程占地多,输水损失大m小, 边坡不稳定取值：（１）土质好（粘重），ｍ小（２）流量大，水深大，则ｍ大参考表4-9，4-10。

４．宽深比b渠底宽与设计水深之比有三种宽深比（１）水力最优断面宽深比特点: 断面窄深, 适用于小型渠道。

（２）满足相对稳定的宽深比相对平稳：不冲不淤或冲淤平稳对于一般渠道：多沙河流上引水的渠道:（３）实用经济断面宽深比水力最优断面，虽然过水断面小，但由于其断面比较窄深，对大型渠道并不适用（为什么？因为不易施工，易塌）。

为克服最优水力断面的缺点（加大底宽，减小水深），同时又使过水断面面积接近于最优水力断面的断面面积，因而提出实用经济断面宽深比。

计算方法：例已知某渠道设计流量为20.3m3/s，渠底比降ｉ＝1/5000,沿线土质为粘壤土。

分别计算最优水力断面、实用经济断面、相对稳定断面的设计水深和底宽。

解：（１）最优水力断面最优水力断面水深计算公式为b = 0.828*4.88 =4.04(m)（２）实用经济断面（３）相对稳定断面最优水力断面水深最大，实用经济断面次之。

如 ： ０ ０， ５ ６６ ８ ９ ３７，９ ６ ． ２ ； ０＋ ０ ３ ７ ４ ． ０ ５ １４ ５ ６６ １ ０＋１ ０ ０，
ＨＡＯ ｏ ｇ—ｚ Ｚ ｎ ｅ
（ ｈ ｉ ｔ ａ ｅ ｆ ｎ ｉｅｒ ｇＳ ｒ ｅｉｇａ ｄＭａ ｐｎ ｆ ｈ ａ ｘ Ｐ ｏ ｉｃ ， ｉ ｎ７ ０５ ， ｈｎ ） Ｔ ｅＦｒ ｄ ｍｙｏ ｇ ｅｉ ｕ ｖｙｎ ｎ ｐ ｉｇｏ ａ ｎ ｉ ｒｖｎ ｅＸ １０ ４ Ｃ ｉａ ｓ Ａｃ Ｅ ｎ ｎ Ｓ ａ
作 方法 。
范要 求 ， 应用 Ｖｓａ Ｂｓ ． 件 开 发 平 台 设计 编写 横 ｉ ｌ ａｉ ６０软 ｕ ｃ 断 面数据 处理 系统 。在该 系 统 中将 横 断 面数据 导 人 数据 库后 ， 生成 横 断面 的预 览 图形 ， 可根 据 图形检 查 断面 的数 据错 误 ， 并输 出 已入 库横 断 面数 据 的错 误记 录 到记 事本 中。编制 Ａ ｔ Ａ ｕ Ｃ Ｄ的脚本命 令组 文件 在 Ａ ｔ Ａ ｏ ｕ Ｃ Ｄ下绘 制 ｏ 横 断面 图形 ， 用 Ａ ｔ Ａ 中 的 Ａ ｔ ａｏ 查横 断 面 利 ｕ ＣＤ ｏ ｕ ｍ ｔｎ检 ｏ ｉ 基点坐 标 。该 系统 可实 现横 断 面数 据 处 理及 应 用 的一 体 化、 可视 化 ， 用于 处理 大 规模 横 断面 数据 处理 及其 他 线 适
ｄａａ ｔ．
Ｋｅ ｒ ｓ Ａｕ ｏ ＡＤ； ｒ ｓ ｅ ｔ ｎ Ｗｉ ｄ ｗｓｏ ｅ ａ ｉｇ；ｃ ｐ ｏ ｙ ｗｏ ｄ ： ｔ Ｃ ｃ ｏ ｓ ｓ ｃｉ ； ｎ ｏ ｐ ｒ ｔ ｏ ｎ ｓ ｒ ｔｃ ｍｍａ ｄ ｇｏ ｐ ｄ ｔｂ ｓ ｅ ｌｔ ｐ ｉ ｔｅｒ ｒ ｉ ｎ ｕ ； ａａ ａ ｅ ｔｍｐ ａｅ； ｏ ｎ ｒ ｒ ｏ
性 横断 面数 据 处 理 。经 过 实践 检 验 ， 系 统 的 应 用 极 大 该

cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
此课件下载可自行编辑修改，供参考！ 感谢你的支持，我们会努力做得更好！
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
四、编辑道路断面图数据
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
二、生成里程
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤
cass道路土石方横断面图计算详细 步骤

三、路基土石方调配
▪ 土石方调配的目的：确定填方用土的来源、挖方弃土的去向； 以及计价土石方的数量和运量等。
▪ 填方土源：附近挖方利用
▪
借土
▪ 挖方去向：调往附近填方
▪
弃土
▪ （一）土石方调配原则
▪ （1）就近利用，以减少运量；
▪ （2）不跨沟调运；
▪ （3）高向低调运；
▪ （4）经济合理；
（4）经济合理；
二、土石方数量计算
1. 平均断面法： 若相邻两断面均为填方或均为挖方且面积大小相近，则
可假定两断面之间为一棱柱体其体积的计算公式为：
1 V 2 (F1 F2 )L
二、土石方数量计算
1. 平均断面法： 若相邻两断面均为填方或均为挖方且面积大小相近，则
可假定两断面之间为一棱柱体其体积的计算公式为：
平均运距：挖方路段中心桩号至填方路段中心桩号的距离计算。
（3）运量
土石方运量为平均运距与土石方调配数量的乘积。单位：
m3·km
（4）计价土石方数量
计价土石方数量=挖方数量+借方数量 如某工程土石方数量：填方500m3 挖方200m3
借方400m3 弃方100m3 则计价土石方数量=600m3
一般工程的土石方总量，实际上是指计价土石方数量。一条 公路的土石方总量，一般包括路基工程、排水工程、临时工程、 小桥涵工程等项目的土石方数量。
（二）土石方调配方法
土石方计算表调配法：公路设计文件推荐方法。
土石方调配后，应按下式进行复核检查：

横向调运+纵向调运+借方=填方

横向调运+纵向调运+弃方=挖方

挖方+借方=填方+弃方

路基土方工程量计算方法地面形状是很复杂的，填、挖方不是简单的几何体，所以其计算只能是近似的，计算的精确度取决于中桩间距、测绘横断面时采点的密度和计算公式与实际情况的接近程度等。

计算时一般应按工程的要求，在保证使用精度的前提下力求简化。

一、横断面面积计算路基的填挖断面面积，是指断面图中原地面线与路基设计线所包围的面积，高于地面线者为填，低于地面线者为挖，两者应分别计算。

通常采用积距法和坐标法。

1.积距法：如图4-4将断面按单位横宽划分为若干个梯形和三角形，每个小条块的面积近似按每个小条块中心高度与单位宽度的乘积：Ai=b*hi则横断面面积：A=b*h1+b*h2+b*h3+…+b*hn =b∑hi当b=1m时，则A在数值上就等于各小条块平均高度之和∑hi。

2.坐标法：如图4-5已知断面图上各转折点坐标（xi,yi）,则断面面积为：A=[∑（x i*y i+1-x i+1y i)]1/2坐标法的计算精度较高，适宜用计算机计算。

二、土石方数量计算路基土石方计算工作量较大，加之路基填挖变化的不规则性，要精确计算土石方体积是十分困难的。

在工程上通常采用近似计算。

即假定相邻断面间为一棱柱体，则其体积为：V=（A1+A2）*2/L式中：V—体积，即土石方数量（m3）；A1、A2—分别为相邻两断面的面积（m2）；L—相邻断面之间的距离（m）。

L—相邻断面之间的距离（m）。

此种方法称为平均断面法，如图4-5。

用平均断面法计算土石方体积简便、实用，是公路上常采用的方法。

但其精度较差，只有当A1、A2相差不大时才较准确。

当A1、A2相差较大时，则按棱台体公式计算更为接近，其公式如下：V=1/3(A1+A2)L(1+m/(1+m))式中：m=A1/A2其中A1＜A2。

第二种的方法精度较高，应尽量采用，特别适用计算机计算。

用上述方法计算的土石方体积中，是包含了路面体积的。

若所设计的纵断面有填有挖基本平衡，则填方断面中多计算的路面面积与挖方断面中少计算的路面面积相互抵消，其总体积与实施体积相差不大。

一、横断面面积计算路基的填挖断面面积，是指断面图中原地面线与路基设计线所包围的面积，高于地面线者为填，低于地面线者为挖，两者应分别计算。

通常采用积距法和坐标法。

1.积距法：如图4-4将断面按单位横宽划分为若干个梯形和三角形，每个小条块的面积近似按每个小条块中心高度与单位宽度的乘积：Ai=b hi则横断面面积： A =b h1+b h2+b h3+… +b hn=b∑ hi当 b = 1m 时，则 A 在数值上就等于各小条块平均高度之和∑ hi。

2.坐标法：如图4-5已知断面图上各转折点坐标（xi,yi）, 则断面面积为：A = [∑（xi yi+1-xi+1yi) ] 1/2坐标法的计算精度较高，适宜用计算机计算。

图4-4 横断面面积计算(积距法)h 4h 1h 2h 3hn A图4-5 横断面面积计算(坐标法)5,y 5)二、 土石方数量计算路基土石方计算工作量较大，加之路基填挖变化的不规则性，要精确计算土石方体积是十分困难的。

在工程上通常采用近似计算。

即假定相邻断面间为一棱柱体，则其体积为：V=（A 1+A 2） 2L 式中：V — 体积，即土石方数量（m 3）；A 1、A 2 — 分别为相邻两断面的面积（m 2）；L —相邻断面之间的距离（m ）。

此种方法称为平均断面法，如图4-5。

用平均断面法计算土石方体积简便、实用，是公路上常采用的方法。

但其精度较差，只有当A1、A2相差不大时才较准确。

当A1、A2相差较大时，则按棱台体公式计算更为接近，其公式如下：V=31(A 1+A 2) L (1+mm 1) 式中：m = A 1 / A 2 ，其中A 1 ＜A 2 。

图4-5 平均断面法第二种的方法精度较高，应尽量采用，特别适用计算机计算。

用上述方法计算的土石方体积中，是包含了路面体积的。

若所设计的纵断面有填有挖基本平衡，则填方断面中多计算的路面面积与挖方断面中少计算的路面面积相互抵消，其总体积与实施体积相差不大。

如何进行道路纵横断面测量与计算道路纵横断面测量与计算是道路设计和规划过程中必不可少的一环。

它涉及到道路的几何形状、交通流量分布以及排水系统等方面的设计，对于确保道路的安全和顺畅起到重要的作用。

本文将介绍几个关键步骤以及常用的测量与计算方法。

首先，进行道路纵横断面测量前，需要准备一些必要的工具和设备。

测量常用的工具包括测量尺子、水平仪、锤子、彩色标记笔等。

此外，需要地形测量仪和全站仪等高精度测量设备来获取地形数据。

在使用测量设备时，需要确保其正确校准和准确放置，以保证测量结果的准确性。

其次，进行道路纵横断面的测量。

在测量过程中，首先需要确定测量起点和终点，并设置基准点。

然后，按照事先设定的间距，在道路纵向上进行横截面的测量。

可以选择两侧对称测量，或者根据具体需要进行单侧测量。

在每个测量点上，使用测量尺子等工具测量路面的高程，并记录在测量表格中。

同时，还需要记录道路的宽度、道路边线、沟槽、护栏等交通设施的位置和尺寸。

然后，进行道路纵横断面的计算。

在计算过程中，可以利用道路纵断面图和测量数据，使用数学和图形计算方法进行计算。

首先，计算道路各截面的纵坡、横坡和高程等参数。

根据测量数据计算出每个测量点的高程值，并根据高程值的变化来计算纵坡。

然后，通过比较不同测量点的高程值，计算出横坡和弯曲度等参数。

最后，绘制纵断面图和横断面图，并进行数据分析和评估。

在进行道路纵横断面测量与计算时，还需要考虑几个关键因素。

首先是实际测量中的误差和不确定性。

测量中可能会存在测量误差和仪器偏差，因此需要在计算过程中进行相应的调整和修正。

其次是道路设计的要求和标准。

根据不同的设计需求，可能需要对测量和计算结果进行调整和优化。

最后是数据的处理和存储。

测量和计算得到的数据应该进行合理的归档和管理，方便日后的查阅和使用。

综上所述，道路纵横断面测量与计算是一个复杂而关键的环节，直接影响着道路设计和规划的质量和效果。

在进行测量和计算时，需要准备好相应的工具和设备，并确保其正确使用和校准。

如何进行横断面测绘与计算近年来，横断面测绘与计算在各个领域得到了广泛的应用。

无论是城市规划、道路建设还是水利工程，准确绘制横断面并进行相关计算都起着至关重要的作用。

本文旨在探讨如何进行横断面测绘与计算，并介绍相关的方法和工具。

横断面测绘是指根据地形特征，在某一特定位置沿垂直于某一线路或水流方向的平面上测绘地形的高程及各种要素，如道路、河流、建筑物等。

横断面测绘的首要任务是确定测绘线路和测量基线，在测量过程中需要使用一系列仪器和工具，如全站仪、水平仪、高程杆等。

在进行测绘时，需要注意选择合适的孔距与测点数量，以保证数据的准确性和可靠性。

测绘完成后，接下来就是进行横断面计算。

横断面计算主要包括曲线平差和剖面面积计算两个方面。

曲线平差是指将不连续的测量点通过曲线拟合与平均滤波等方法，得到一条平滑的横断面曲线。

而剖面面积计算则是根据测量点的坐标和高程数据，计算出各个部分的面积，常用的方法有梯形法、辛普森公式等。

在实际操作中，为了提高测绘和计算效率，人们还开发了许多辅助工具和软件。

比如，目前市场上有很多流行的测绘软件，如AutoCAD、ArcGIS等，它们可以帮助工程师更快、更精确地完成横断面测量和计算工作。

此外，还有一些专门为横断面测绘和计算设计的软件，例如LandSlope、LandXplorer等，它们提供了更多专业的功能和工具，能够满足复杂工程项目的需求。

除了软件工具，还有一些其他的测绘与计算方法值得关注。

例如，无人机测绘技术在横断面测绘领域得到了广泛应用。

通过搭载高精度相机或激光雷达等设备，无人机可以在短时间内获取大面积地形数据，并通过专门的软件进行后期计算和分析。

相比传统的测绘方法，无人机测绘具有成本低、速度快、数据准确等优势，逐渐成为横断面测绘的主要手段之一。

此外，在实际应用过程中，还需要考虑一些技术难题和实际问题。

例如，地形复杂、测量环境恶劣、数据质量不稳定等因素都可能对测绘和计算结果造成影响。

其中 ｄ ＝∑ｄ一 ， ｓ 前 垂 到中 的 ：ｌ ｓ ｓ ∑ｄ为 一 线 １ 桩
图 １
水平距离 ；
如采 用 手 工 在 厘 米 纸 上 绘 图 ， 人 工 计 算 ， 用 主 要从 图上 量 取 ， 作 量 大 ， 度 低 。而 采 用 计 算 机 工 精
ｈ ２为包含 的顶 点作 垂 线 与地 面 线 （ 点在 设 １ 顶
（２） ｈ ） ｄ ２ ｄ —ｄｌ ｈ 一 ｈ ｈ
施 工单 位为 了提高 土 方 量 的精 度 ， 断 面 的 间距 都 横 较 小 ， 土方 成本 大的地 方 ， 的甚 至 ５Ｉ 量 一个 在 有 ｎ测
断面 。
１ ２ 标 准断 面 ． １ ）对 于复测 后 的断 面 与 原 设计 单 位 勘 测 的相
差不 大 ， 为施 工单 位来 说 ， 准 断 面都 是 由设 计 作 标 图纸 确定 ， 工 单 位 不 得 变 更 。 （ 施 而设 计 阶 段 的标
计 线上 ） 或设计 线 （ 点在 地面 线上 ） 顶 相交 的距离 。
第５ 期
童新 建等 ： 公路施工 中横断面 图的绘制和土方计算程序设计
Ｉ １ ＊ ｈ ＞ ０ Ｔｈ ｎ ｛ｈ ２ ｅ
４ ５
对 于 （） ｃ 图形 ， 含 设 计 线 与地 面线 相 交 点 ， 包 面
积为 ：
第 ３ 卷第 ５ １ 期
２０ ０８年 ９月
现
代
测
绘
Ｖ０ ． ， ． １ ３１ Ｎｏ ５
Ｓ ｐ２ ０ ｅａ ｄ Ｍ ａ ｐｎ ｄ ｒ ｕ ｖ ｙｎ ｎ ｐ ｉｇ
公 路 施 工 中横 断面 图的 绘制 和 土 方计 算 程序 设 计
准断 面可 以 自由确 定 ）