《圆》单元测试卷

人教版小学六年级数学第5单元《圆》单元测试卷一、填空题。

1．半径决定圆的（），圆心决定圆的（）。

2．画一个周长是18.84 cm的圆，圆内最长的线段是（）cm，所画出的圆的面积是（）cm2。

3．淘气用一个圆规画一个直径是 6 厘米的圆，圆规针尖的位置是圆的（），圆规两脚之间的距离是（）厘米，这个圆的周长是（）厘米，面积是（）平方厘米。

4．自行车的车轮溶动一周，所行的路程就是车轮的（）。

5．一个圆的直径扩大到原来的 3 倍，它的周长扩大到原来的（）倍，面积就扩大到原来的（）倍。

6．有一个钟面，它的分针长3分米，时针长2分米。

从6时到9时，分针的针尖走过的路程是（）分米；时针扫过的面积是（）平方分米。

7．已知一个挂钟的时针长度是分针的3，转动一小时后，时针扫过的面积是分4针的（）。

8．大圆的半径与小圆的直径相等，那么大小两个圆的周长比是（），它们的面积比是（）。

9．画一个圆，圆规两脚间的距离是3cm，那么，这个圆的周长是（），面积是（）。

10．一个圆的周长是12.56厘米，它的面积是（）。

二、选择题。

1．把一个直径是2cm 的圆分割成两个半圆形后，每个半圆形的周长是( )cm。

A．6.28 B．3.14 C．4.14 D．5.142．圆的（）是圆中最长的线段。

A．周长B．直径C．半径3．画圆时，圆规两脚间的距离是圆的（）。

A．半径B．直径C．周长4．一个圆的直径由原来的 3 厘米增加到 7 厘米，周长增加了（）厘米。

A．6.28 B．12.56 C．25.12 D．50.245．将一个圆形纸片沿着它的直径剪成两半，它的面积和周长（）。

A．面积不变周长增加B．面积增加周长不变C．面积周长都不变D．面积周长都增加6．在一个长 5 cm ，宽 3 cm 的长方形中画一个最大的半圆，这个半圆的直径是（）。

A．1.5 cm B．3 cm C．5 cm D．6 cm7．一个圆的直径与周长的比是（）A．1：2πB．1：πC．2：π8．淘气和笑笑分别在本子上画了一个大圆和小圆，两个圆的圆周率（）A．淘气的大B．笑笑的大C．一样大D．无法比较9．用圆规画一个周长是6.28cm的圆，这个圆的半径是（）cm。

[详解]作PE⊥OA于E，
∵OP=1，∠POE=45°，
∴OE=PE= ，即点P的坐标为（ ， ），
则第2秒P点为（0，1），
根据题意可知，第3秒P点为（- ， ），第4秒P点为（-1，0），第5秒P点为（- ，- ），第6秒P点为（0，-1），
第7秒P点为（ ，- ），第8秒P点为（1，0），
2018÷8=252……2，
A. B. πC. πD. π
11.如图，A B是⊙O的直径，C，D是圆上两点，连接A C，B C，A D，C D．若∠C A B=55°，则∠A D C的度数为（ ）
A. 55°B. 45°C. 35°D. 25°
12.如图，在矩形A B C D中，A B=3，B C=4，O为矩形A B C D对角线的交点，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（）
A. 44°B. 54°C. 62°D. 72°
3.如图，A B、C D分别与半圆OO切于点A，D，B C切⊙O于点E，若A B=4，C D=9，则⊙O 半径为（ ）
A. 12B. C. 6D. 5
4.如图，△A B C是⊙O的内接三角形，A B为⊙O的直径，点D为⊙O上一点，若∠A C D＝40°，则∠B A D的大小为（ ）
16.如图，Rt△A B C中，A B⊥B C，A B=6，B C=4，P是△A B C内部的一个动点，且满足∠PA B=∠PB C，则线段CP长的最小值为_____．
17.如图，在Rt△AOB中，∠AOB＝90°，OA＝3，OB＝2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接A D，则图中阴影部分面积是_____．

《圆》单元测试卷一、选择题：1．如图，⊙O中弧AB的度数为60°，AC是⊙O的直径，那么∠BOC等于 ( ) A．150° B．130° C．120° D．60°AB、相交于P，则下列结论正确的是（）2．如图，⊙O中，弦CDA．PA·AB＝PC·PD B． PA·AB＝PC·CDC．PA·PB＝PC·PD D． PA·PD＝PC·PB3．一条弦分圆为1∶5两部分，则这条弦所对的圆周角的度数为（）A．300 B．1500 C．300或1500 D．不能确定4．下列命题是真命题的是（）A、垂直于圆的半径的直线是圆的切线B、经过半径外端的直线是圆的切线C、直线上一点到圆心的距离等于圆的半径的直线是圆的切线D、到圆心的距离等于圆的半径的直线是圆的切线5．⊙O的半径为R，圆心到点A的距离为d，且R、d分别是方程x2－6x＋8＝0的两根，则点A与⊙O的位置关系是（）A．点A在⊙O内部 B．点A在⊙O上C．点A在⊙O外部 D．点A不在⊙O上6．如图，在平面直角坐标系中，⊙O′与两坐标轴分别交于A、B、C、D四点.已知：A（6， 0），B（0，－3），C（－2，0），则点D的坐标是（）A．（0，2） B．（0，3） C．（0，4） D．（0，5）7．如图，A、B是⊙O上的两点，AC是⊙O的切线，∠OBA=75°，⊙O的半径为1，则OC的长等于（）图3P BCOADA、32 B 、22 C 、233D 、2 二、填空题：1．已知AB 是⊙O 的直径，CB 与⊙O 相切于点B ，AC ＝2AB ，则∠ACB ＝ 。

2．在△ABC 中,∠ACB=90°.AC=2cm,BC=4cm,CM 是中线,以C 为圆心以5cm 长为半径画圆则A 、B 、M 三点在圆外的是 ，在圆上的是 。

8.如图,△A B C是⊙O的内接三角形,∠C＝30°,⊙O的半径为5,若点P是⊙O上的一点,在△A BP中,PB＝A B,则PA的长为()
A.5B. C.5 D.5
[答案]D
[解析]
试题解析：连接OA、OB、OP,
∵∠C=30°,∴∠APB=∠C=30°,∵PB=A B,∴∠PA B=∠APB=30°
A.π+1B.π+2C.2π+2D.4π+1
8.如图,△A B C是⊙O的内接三角形,∠C＝30°,⊙O的半径为5,若点P是⊙O上的一点,在△A BP中,PB＝A B,则PA的长为()
A. 5B. C. 5 D. 5
9.如图是某公园的一角,∠AOB=90°,弧A B的半径OA长是6米,C是OA的中点,点D在弧A B上,C D∥OB,则图中休闲区(阴影部分)的面积是()
23.如图,点I是△A B C的内心,AI的延长线和△A B C的外接圆相交于点D,与B C相交于点E．
(1)求证：DI=D B；
(2)若AE=6Cm,ED=4Cm,求线段DI的长．
24.如图,已知扇形AOB的圆心角为直角,正方形OC DE内接于扇形AOB．点C、E、D分别在OA、OB、弧A B上,过点A作AF⊥DE交ED的延长线于F,如果正方形的边长为1,求阴影部分M、N的面积和．
点睛：本题考查了圆周角定理,圆周角的度数等于它所对的弧所对的圆心角度数的一半,圆的弦所对的圆周角分两种,一种是优弧所对的圆周角,一种是劣弧所对的圆周角,它们是互补的关系.
4.⊙O的半径r＝5Cm,直线l到圆心O的距离D＝4,则l与⊙O的位置关系是( )
A.相离B.相切C.相交D.重合
[答案]C
[解析]
3.正六边形内接于圆,它的边所对的圆周角是( )

六年级数学上册《圆》单元测试卷六年级上册《圆》单元测试卷一、填空题不困难，全对不简单。

（10分）1.圆的半径扩大到原来的5倍，周长扩大到原来的25倍，面积扩大到原来的25倍。

2.圆有无数条对称轴。

3.同一个圆中，圆的周长是直径的π倍，直径与周长的比是1:π。

4.大圆和小圆的直径比是3:2，周长比是3:2，面积比是9:4.5.一个时钟的分针长20cm，45分钟分针所走的路程是15cm，它扫过的面积是150cm²。

6.一个车轮的外直径是1.5m，它滚动一周的距离是4.5m。

二、我是小法官，对错我来判。

（10分）7.错误。

8.正确。

9.错误。

10.正确。

11.错误。

三、脑筋转转转，答案全发现。

（10分）12.C。

13.A。

14.B。

15.B。

16.A。

四、填空题。

（18分）17.半径（r）：2.5cm直径（d）：5cm周长（C）：15.7cm面积（S）：19.63cm²五、动动小脑瓜，一起画一画。

（6分）18.画出的图形如下：正方形面积为9cm²，圆的面积为7.07cm²，它们的比值为9:7.07.19.对称轴如下图所示：无法插入图片，请见谅）六、计算。

20.1）①周长为18.84cm，②半径为2.5dm。

2）①半径为1.57dm，②直径为16m。

21.阴影部分的面积为25π-50cm²。

22.阴影部分的面积为16π-32cm²。

23.某小区有一片半径为15m的半圆形绿地，要求计算这片绿地的周长。

24.一个圆形养鱼池的直径是20m，平均每平方米水面投放鱼苗15尾，需要计算这个养鱼池一共要投放鱼苗多少尾。

25.在一个圆形花坛的周围修建一条宽1m的甬路，花坛的周长是125.6m，需要计算这条甬路的占地面积。

26.已知一个正方形的面积为9cm²，以它的边长为半径画圆，需要计算这个圆的面积。

27.杂技演员表演独轮车走钢丝，车轮的直径为40cm，需要计算车轮在骑过31.4m长的钢丝时需要转动多少周。

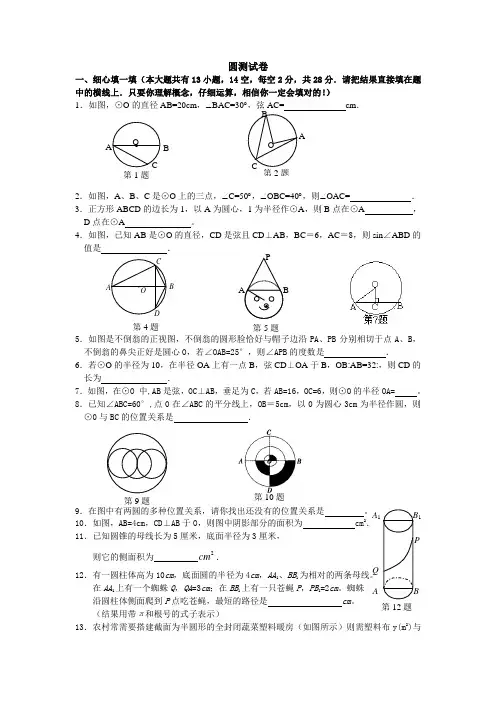
第2题 B第4题圆测试卷一、细心填一填（本大题共有13小题，14空，每空2分，共28分．请把结果直接填在题中的横线上．只要你理解概念，仔细运算，相信你一定会填对的！）1．如图，⊙O 的直径AB=20cm ，∠BAC=30︒，弦AC= cm ．2．如图，A 、B 、C 是⊙O 上的三点，∠C=50︒，∠OBC=40︒，则∠OAC= ．3．正方形ABCD 的边长为1，以A 为圆心，1为半径作⊙A ，则B 点在⊙A ，D 点在⊙A 。

4．如图，已知AB 是⊙O 的直径，CD 是弦且CD ⊥AB ，BC ＝6，AC ＝8，则sin ∠ABD 的值是 ．5．如图是不倒翁的正视图，不倒翁的圆形脸恰好与帽子边沿PA 、PB 分别相切于点A 、B ，不倒翁的鼻尖正好是圆心O ，若∠OAB=25°，则∠APB 的度数是 ．6．若⊙O 的半径为10，在半径OA 上有一点B ，弦CD ⊥OA 于B ，OB ׃AB=3׃2，则CD 的长为 ．7．如图，在⊙O 中,AB 是弦，OC ⊥AB ，垂足为C ，若AB=16，OC=6，则⊙O 的半径OA= 。

8．已知∠ABC=60°,点0在∠ABC 的平分线上，OB ＝5cm ，以0为圆心3cm 为半径作圆，则⊙0与BC 的位置关系是 ．9．在图中有两圆的多种位置关系，请你找出还没有的位置关系是 。

10．如图，AB=4cm ，CD ⊥AB 于O ，则图中阴影部分的面积为 cm 2．11．已知圆锥的母线长为5厘米，底面半径为3厘米， 则它的侧面积为 2cm ．12．有一圆柱体高为10cm ，底面圆的半径为4cm ，AA 1、BB 1为相对的两条母线。

在AA 1上有一个蜘蛛Q ，QA =3cm ；在BB 1上有一只苍蝇P ，PB 1=2cm 。

蜘蛛 沿圆柱体侧面爬到P 点吃苍蝇，最短的路径是 cm 。

（结果用带π和根号的式子表示）13．农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房（如图所示）则需塑料布y(m 2)与B第1题 第5题A B 1 A 1 BQ P第12题 第9题第10题半径R(m)的函数关系式是（不考虑塑料埋在土里的部分） .二、精心选一选（本大题共7小题，每小题3分，共21分. 在每小题所给出的四个选项中，只有一项是正确的.把所选项前的字母代号填在题后的括号内. 只要你掌握概念，认真思考，相信你一定会选对！）14．三角形的内心是 （ ）A ．三条中线的交点B ．三边垂直平分线的交点C ．三条角平分线的交点D ．三条高的交点15．下列说法中正确的是 （ ）A ．经过三个点一定可以作一个圆B ．一个圆一定有一个内接三角形，并且只有一个内接三角形C ．一个三角形有且只有一个内切圆，并且一个圆有且只有一个外切三角形D ．任意三角形有且只有一个外接圆和一个内切圆16．如图，⊙O 1的半径为5cm ，⊙O 2经过O 1并且半径为2cm ，O 1、O 2在直线l 上，⊙O 2沿直线l 移动．当⊙O 2平移 cm 时与⊙O 1外切． （ ）A ．1或5B ．1或C ．5或7D ．5或917．⊙O 的半径为5cm ，点P 在直线l 上，若OP=5cm ，则直线l 与⊙O的位置关系是 （ ） A ．相离 B 。

第1页 共4页 第2页 共4页…………○…………内…………○…………装…………○…………订…………○…………线…………○…………人教版六年级数学上册《圆》测试卷学校:______姓名:______班级:______题号 一 二 三 四 五 总分 得分一、选择题1.以一点为圆心可以画出( )个圆。

A.1B.2C.3D.无数2.盒子里刚好放下五瓶罐头，盒子的长是30cm ，每瓶罐头底面的半径是( )。

A.10cmB.5cmC.3cmD.4cm3.下面各圆中的阴影部分，( )是扇形。

A.B.C.D.4.画圆时，如果圆规两脚间张开的距离是4厘米，那么画出的圆的周长是( )厘米。

A.8B.12.56C.18.84D.25.125.在研究圆环的面积时，陈军借助研究圆面积公式时所用的方法，把圆环等分成16份，外圆半径用R 表示，内圆半径用r 表示，拼成一个近似的平行四边形。

他发现平行四边形的底是( )。

A.πRB.πrC.πR −πrD.πR +πr二、判断题6.两端都在圆上的所有线段中，直径最长。

( )7.圆的周长是半径的6.28倍。

( )8.把一个圆沿直径剪开，所得半圆的面积是原来圆面积的一半。

( )9.圆越大圆周率越大，圆越小圆周率越小。

( )三、填空题10.在一张边长是8厘米的正方形纸上画一个最大的圆，圆的半径是( )厘米；画一个最大的半圆，半圆的半径是( )厘米。

11.半圆也是一个扇形，它的圆心角是（ ）∘。

12.在一张长40cm 、宽6cm 的长方形铁皮上剪下一个最大的圆，圆的周长是（）cm 。

13.一个挂钟的时针长5厘米，这根时针的尖端一昼夜走了( )厘米。

14.如图所示，正方形的面积是20平方厘米，圆的面积是( )平方厘米。

15.一种自动旋转的喷水装置，它的喷灌面是一个半径为6米的圆形，这种装置的喷灌面积是( )平方米。

四、图形计算题16.计算下列图形的周长。

（单位：cm ）(1)(2)17.求下面各图形阴影部分的面积。

故选A．
【点睛】本题考查了圆柱的计算，解题的关键是熟知圆柱的侧面积的计算方法．
11. 在直角坐标系中的位置如图所示，若将 绕点 旋转，点 的对应点为点 ，其中 ， ， ， ，则旋转后点 的对应点 的坐标为（）
A. B. C. D.
【答案】D
【解析】
分析】
根据旋转的性质作出旋转后的图形，写出点A对应点的坐标即可得解．
【详解】连结BC．
∵OB=OC，∴∠OBC=∠OCB．
∵∠ABO=∠ACO，∴∠ABC=∠ACB，∴AB=AC，∴ = = ，故A、B、C正确，不符合题意；
∠BOC的度数无法求出，故D错误，符合题意．
故选D．
【点睛】本题考查了圆心角、弧、弦的关系定理：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等；同时考查了等腰三角形的判定与性质．
指出其旋转中心和旋转的角度
求 的长度；
与 的位置关系如何？说明理由．
24.想一想：如图称为太极图，圆形图案由两条形状和大小完全一样的白鱼和黑鱼组成，也称为“阴阳鱼”，若太极图的直径为 ，你能算出一条白鱼或黑鱼的面积吗？
25.已知 是 的直径，点 是 延长线上一点， ， 是 的弦， ．
（1）求证：直线 是 的切线；
设圆心角为n，有 =2πr=πR，
∴n=180°．
故选B．
考点：圆锥的计算
8.如图，直线 经过 的圆心，与 相交于 、 两点，点 在 上，且 度．点 是直线 上的一个动点（与点 不重合），直线 交 于 ，则使 的点 共有（）
A.1个B.2个C.3个D.4个
【答案】C
【解析】
【分析】
作图，根据等腰三角形的性质和三角形的内角和、外角的性质求解即可.

圆单元测试卷一、选择题（每题2分，共20分）1. 圆的周长公式是（）。

A. C = πdB. C = 2πrC. C = πrD. C = 2πd2. 圆的面积公式是（）。

A. A = πr²B. A = 2πrC. A = πdD. A = πd²3. 半径为2厘米的圆的周长是（）厘米。

A. 4πB. 6.28C. 12.56D. 25.124. 半径为3厘米的圆的面积是（）平方厘米。

A. 9πB. 28.26C. 45D. 28.55. 圆的直径是半径的（）倍。

A. 1B. 2C. 3D. 46. 圆的半径增加1厘米，其面积增加（）平方厘米。

A. πB. 2πC. 3πD. 4π7. 圆的直径是10厘米，其周长是（）厘米。

A. 31.4B. 62.8C. 314D. 6288. 圆的半径是5厘米，其直径是（）厘米。

A. 10B. 15C. 20D. 259. 圆的半径是4厘米，其周长是（）厘米。

A. 12.56B. 25.12C. 50.24D. 100.4810. 圆的半径是6厘米，其面积是（）平方厘米。

A. 113.04B. 36πC. 108D. 36二、填空题（每题2分，共20分）11. 半径为r的圆的周长是______。

12. 半径为r的圆的面积是______。

13. 如果一个圆的周长是31.4厘米，那么它的半径是______厘米。

14. 如果一个圆的面积是28.26平方厘米，那么它的半径是______厘米。

15. 两个圆的半径之比是3:2，那么它们的面积之比是______。

16. 一个圆的直径是20厘米，那么它的周长是______厘米。

17. 一个圆的半径是8厘米，那么它的直径是______厘米。

18. 一个圆的周长是50.24厘米，那么它的半径是______厘米。

19. 一个圆的面积是78.5平方厘米，那么它的半径是______厘米。

20. 如果一个圆的半径增加2厘米，那么它的面积增加______平方厘米。

人教版六年级上册数学第五单元《圆》单元测试卷（含答案）一、认真审题，填一填。

(每小题2分，共18分)1．战国时期墨家所著的《墨经》一书中记载：“圆，一中同长也。

”它表示圆上任意一点到( )的距离相等，也就是圆的( )都相等。

2．白居易的《府西池》中“柳无气力枝先动，池有波纹冰尽开”描述了雨点打在水面上荡开层层的波纹。

已知水池是长6 m、宽5 m的长方形，当波纹到池边时，所形成的最大整圆的周长是( ) ，面积是( )。

3．一个时钟的分针长5 cm，当它走一圈时，它的尖端走了( )cm，分针扫过部分的面积是( )cm2。

4．如右图，把一个圆分割，拼成近似的长方形。

已知这个长方形的周长比圆的周长大10 cm，这个圆的周长是( ) cm，面积是( ) cm2。

5．坐落于辽宁省沈抚新区的“生命之环”，无论是高度还是形式都是世界独有的。

它近似于一个圆环，它的外直径是170米，内直径是150米，则“生命之环”的面积约是( )平方米。

6．一种小汽车的轮子的直径是40厘米，小汽车在行驶过程中轮子每分钟大约转1000圈，这辆小汽车每小时大约行驶( )千米。

(取整千米数)7．如图，在长方形内有甲、乙、丙三个圆，已知乙、丙两个圆相同，那么甲、乙两个圆的周长比是( )，面积比是( )。

(第7题图)) (第8题图)) (第9题图))8．如图，等边三角形的边长是6 cm ，则涂色部分的面积是( )cm 2，空白部分的周长是( )cm 。

9．一面镜子的形状如图，它是由1个正方形和4个直径相等的半圆形组成的，半圆形的直径是6 dm ，在镜子周围镶上铝边，需要铝边长( )dm ，镜子的面积是( )dm 2。

二、仔细推敲，选一选。

(将正确答案的序号填在括号里)(每小题2分，共12分) 1．如图，圆从点A 开始，沿着直尺向右滚动一周到达点B ，点B 的位置大概在( )。

A ．9到10之间 B ．10到11之间 C ．11到12之间2．如图，从甲到乙，走a 路线与走b 路线的路程相比，( )。

人教版数学九年级上学期《圆》单元测试(满分120分，考试用时120分钟)一、单选题OP ，则点P与O的位置关系是( ) 1．已知O的半径为5，同一平面内有一点P，且7A．点P在圆内B．点P在圆上C．点P在圆外D．无法确定2．已知正六边形的边长是2，则该正六边形的边心距是()A．1 B C．2 D．23．如图，已知在⊙O中，BC是直径，AB＝DC，∠AOD＝80°，则∠ABC等于( )A．40°B．65°C．100°D．105°4．如图，ABCD为⊙O内接四边形，若∠D=85°，则∠B=( )A．85°B．95°C．105°D．115°5．如图，已知AB是⊙O直径，∠AOC＝130°，则∠D等于()A．65°B．25°C．15°D．35°6．如图，AB是⊙O的直径，C，D为⊙O上的点，AD CD，如果∠CAB＝40°，那么∠CAD的度数为()A．25°B．50°C．40°D．80°7．已知⊙O的半径为4，直线l上有一点与⊙O的圆心的距离为4，则直线l与⊙O的位置关系为() A．相离B．相切C．相交D．相切、相交均有可能8．在平面直角坐标系中，以原点O为圆心，5为半径作圆，若点P的坐标是(3，4)，则点P与⊙O的位置关系是()A．点P在⊙O外B．点P在⊙O内C．点P在⊙O上D．点P在⊙O上或在⊙O外9．若⊙A的半径为5，圆心A的坐标是(1，2)，点P的坐标是(5，2)，那么点P的位置为()A．在⊙A内B．在⊙A上C．在⊙A外D．不能确定10．如图，AB是⊙O直径，若∠AOC＝140°，则∠D的度数是()A．20°B．30°C．40°D．70°11．如图，MN是⊙O的直径，MN＝4，∠AMN＝30°，点B为弧AN的中点，点P是直径MN上的一个动点，则P A+PB的最小值为()A．4 B．C．D．212．“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材，埋在壁中，不知大小，，以锯锯之，深一寸，锯道长六寸，问径几何？”用现代的数学语言表述是:“CD为O的直径，弦AB CD垂足为E，CE=1寸，AB=10寸，求直径CD的长”，依题意得CD的长为( )A．12寸B．13寸C．24寸D．26寸二、填空题13．如图，AB是⊙O的直径，D是AB延长线上一点，DC切⊙O于C，连接AC，若∠CAB＝30°，则∠D ＝_____度．14．如图，已知AB是⊙O的直径，AB=2，C、D是圆周上的点，且∠CDB=30°，则BC的长为______.15．若一个扇形的圆心角为45°，面积为6π，则这个扇形的半径为_______．16．如图，用一个半径为30cm，面积为300πcm2的扇形铁皮，制作一个无底的圆锥(不计损耗)，则圆锥的底面半径r为______．三、解答题17．已知如图所示，OA、OB、OC是⊙O的三条半径，弧AC和弧BC相等，M、N分别是OA、OB的中点．求证:MC=NC．18．如图，AB为⊙O的直径，过点C的切线DE交AB的延长线于点D，AE⊥DC，垂足为E．求证:AC平分∠BAE．19．如图，四边形ABCD 是⊙O 的内接四边形，BD 是∠ABC 的角平分线，过点D 分别作DE ⊥AB ，DF ⊥BC ，垂足分别为E 、F ．(1)求证:△AED ≌△CFD;(2)若AB ＝10，BC ＝8，∠ABC ＝60°，求BD 的长度．20．如图，矩形ABCD 中，3AB =，4AD =．作DE ⊥AC 于点E ，作AF ⊥BD 于点F ．(1)求AF 、AE 的长;(2)若以点A 为圆心作圆， B 、C 、D 、E 、F 五点中至少有1个点在圆内，且至少有2个点在圆外，求A的半径 r 的取值范围．21．如图，已知O ．(1)用尺规作正六边形，使得O 是这个正六边形的外接圆，并保留作图痕迹; (2)用两种不同的方法把所做的正六边形分割成六个全等的三角形．22．校运会期间，小捷同学积极参与各项活动．在铅球项目中，他掷出的铅球在场地上压出一个小坑(图示是其主视图)，经测量，其中坑宽AB为8cm，小坑的最大深度为2cm，请帮助小捷同学计算铅球的半径OA 的长为多少？23．如图，P是⊙O外一点，P A是⊙O的切线，A是切点，B是⊙O上一点，且P A＝PB，延长BO分别与⊙O、切线P A相交于C、Q两点．(1)求证:PB是⊙O的切线;(2)QD为PB边上的中线，若AQ＝4，CQ＝2，求QD的值．24．如图，O 的直径AB 垂直弦CD 于M ，且M 是半径OB 的中点，8CD cm =，求直径AB 的长．25．如图，四边形ABCD 内接于O ，AB 为O 的直径，点C 为BD 的中点．若40A ∠=，求B ∠的度数．26．如图是破残的圆形轮片，求作此残片所在的圆．(不写作法，保留作图痕迹)参考答案一、单选题12．“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长六寸，问径几何？”用现代的数学语言表述是:“CD 为的直径，弦，垂足为E ，CE=1寸，AB=10寸，求直径CD 的长”，依题意得CD 的长为( )A ．12寸B ．13寸C ．24寸D ．26寸【答案】D 【解析】【分析】连接AO ，设直径CD 的长为寸，则半径OA=OC=寸，然后利用垂径定理得出AE ，最后根据勾股定理进一步求解即可.【详解】如图，连接AO ，设直径CD 的长为寸，则半径OA=OC=寸，∵CD 为的直径，弦，垂足为E ，AB=10寸，∴AE=BE=AB=5寸，根据勾股定理可知， O AB CD⊥2xx 2x x O AB CD ⊥12在Rt △AOE 中，，∴，解得:，∴，即CD 长为26寸.【点评】本题主要考查了垂径定理与勾股定理的综合运用，熟练掌握相关概念是解题关键.二、填空题13．如图，AB 是⊙O 的直径，D 是AB 延长线上一点，DC 切⊙O 于C ，连接AC ，若∠CAB ＝30°，则∠D ＝_____度．【答案】30【解析】【分析】连接OC ，如图，根据切线的性质得∠OCD =90°，再根据等腰三角形的性质和三角形外角性质得到∠COD =60°，然后利用互余计算∠D 的度数．【详解】连接OC ，如图，∵DC 切⊙O 于C ，∴OC ⊥CD ，∴∠OCD =90°．∵OA =OC ，∴∠ACO =∠CAB =30°，∴∠COD =∠ACO +∠CAB =60°，∴∠D =90°﹣∠COD =90°﹣60°=30°． 故答案为30．222AO AE OE =+()22251x x =+-13x =226x=【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径．也考查了等腰三角形的性质． 14．如图，已知AB 是⊙O 的直径，AB=2，C 、D 是圆周上的点，且∠CDB=30°，则BC 的长为______.【答案】1【解析】【分析】根据同弧或等弧所对的圆周角相等可得∠A=∠CDB=30°，再根据AB 是⊙O 的直径，得出∠ACB=90°，则BC=AB ，从而得出结论． 【详解】解:∵AB 是⊙O 的直径，∴∠ACB=90°，∵∠A=∠CDB=30°，∴BC=AB=， 故答案为1．【点评】本题考查了圆周角定理:在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论:半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径．15．若一个扇形的圆心角为45°，面积为6π，则这个扇形的半径为_______．12121212⨯=【答案】【解析】【分析】已知了扇形的圆心角和面积，可直接根据扇形的面积公式求半径长．【详解】设扇形的半径为r．根据题意得:6π解得:r＝故答案为【点评】本题考查了扇形的面积公式．熟练将公式变形是解题的关键．16．如图，用一个半径为30cm，面积为300πcm2的扇形铁皮，制作一个无底的圆锥(不计损耗)，则圆锥的底面半径r为______．【答案】10cm【解析】【分析】根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式得到•2π•r•30=300π，然后解方程即可．【详解】解:根据题意得•2π•r•30=300π，解得r=10(cm)．245360rπ=1212故答案为:10cm．【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．三、解答题17．已知如图所示，OA、OB、OC是⊙O的三条半径，弧AC和弧BC相等，M、N分别是OA、OB的中点．求证:MC=NC．【答案】证明见解析【解析】【分析】根据弧与圆心角的关系，可得∠AOC=∠BOC，又由M、N分别是半径OA、OB的中点，可得OM=ON，利用SAS判定△MOC≌△NOC，继而证得结论．【详解】证明:∵弧AC和弧BC相等，∴∠AOC=∠BOC，∵OA=OB又∵M、N分别是OA、OB的中点∴OM=ON，在△MOC和△NOC中，OM ONAOC BOCOC OC，=⎧⎪∠=∠⎨⎪=⎩∴△MOC≌△NOC(SAS)，∴MC=NC．【点评】此题考查了弧与圆心角的关系以及全等三角形的判定与性质;证明三角形全等是解决问题的关键．18．如图，AB为⊙O的直径，过点C的切线DE交AB的延长线于点D，AE⊥DC，垂足为E．求证:AC平分∠BAE．【答案】证明见解析【解析】【分析】连接OC，根据切线的性质得到OC⊥CD，根据平行线的性质、等腰三角形的性质得到∠EAC=∠CAO，即AC平分∠BAE．【详解】如图:连接OC．∵DE切⊙O于点C，∴OC⊥DE．又∵AE⊥DC，∴OC∥AE，∴∠ACO=∠EAC．∵OA=OC，∴∠ACO=∠OAC，∴∠EAC=∠OAC，∴AC平分∠BAE．【点评】本题考查了切线的性质，掌握圆的切线垂直于经过切点的半径是解题的关键．19．如图，四边形ABCD 是⊙O 的内接四边形，BD 是∠ABC 的角平分线，过点D 分别作DE ⊥AB ，DF ⊥BC ，垂足分别为E 、F ．(1)求证:△AED ≌△CFD;(2)若AB ＝10，BC ＝8，∠ABC ＝60°，求BD 的长度．【答案】(1)见解析【解析】【分析】(1)由角平分线性质定理可得DE ＝DF ，由圆内接四边形性质可得∠A ＋∠BCD ＝180°，然后代换可得∠A ＝∠DCF ，又∠DEA ＝∠F ＝90°， 所以△AED ≌△CFD;(2)由三角形全等可得AE ＝CF ，BE ＝BF ，设AE ＝CF ＝x ，可得x ＝1;在Rt △BFD ，根据30°所对的直角边是斜边的一半，则BD ＝2DF ，利用勾股定理解得BD ＝【详解】(1)∵四边形ABCD 是⊙O 的内接四边形，∴∠A ＋∠BCD ＝180°，又∵∠DCF ＋∠BCD ＝180°，∴∠A ＝∠DCF∵BD 是∠ABC 的角平分线，又∵DE ⊥AB ，DF ⊥BC ，∴DE ＝DF ，∠DEA ＝∠F ＝90°，∴△AED ≌△CFD.(2)∵△AED ≌△CFD ，∴AE ＝CF ，BE ＝BF ，设AE ＝CF ＝x ，则BE ＝10－x ，BF ＝8＋x ，即10－x ＝8＋x ，解得x ＝1，在Rt △BFD ，∠DBC ＝30°，设DF ＝y ，则BD ＝2y ，∵BF 2＋DF 2＝BD 2，∴y 2＋92＝(2y)2，y ＝BD ＝【点评】本题考查了全等三角形的性质和判定，勾股定理等知识，由条件灵活转移线段关系是解题关键. 20．如图，矩形中，，．作DE ⊥AC 于点E ，作AF ⊥BD 于点F ． (1)求AF 、AE 的长;(2)若以点为圆心作圆， 、、、E 、F 五点中至少有1个点在圆内，且至少有2个点在圆外，求的半径 的取值范围．【答案】(1)，;(2) 【解析】【分析】(1)先利用等面积法算出AF=，再根据勾股定理得出; (2)根据题意点F 只能在圆内，点C 、D 只能在圆外，所以⊙A 的半径r 的取值范围为.【详解】解:如图，ABCD 3AB =4AD =A B C D Ar 125AF =165AE = 2.44r <<125165AE = 2.44r <<(1)在矩形中，，．∴∵DE ⊥AC ，AF ⊥BD ，∴ ; ∴AF=， 同理，DE=, 在Rt △ADE 中，=, (2) 若以点为圆心作圆， 、、、E 、F 五点中至少有1个点在圆内，则r>2.4,当至少有2个点在圆外，r<4,故⊙A 的半径r 的取值范围为:21．如图，已知．(1)用尺规作正六边形，使得是这个正六边形的外接圆，并保留作图痕迹; (2)用两种不同的方法把所做的正六边形分割成六个全等的三角形．ABCD 3AB =4AD =11··22ABD S AB AD BD AF ==△125125165A B C D 2.44r <<O O【答案】(1)答案见解析;(2)答案见解析【解析】【分析】(1)利用正六边形的性质外接圆边长等于外接圆半径;(2)连接对角线以及利用正六边形性质．【详解】解:(1)如图所示:,(2)如图所示:【点评】此题主要考查了复杂作图以及全等三角形和正六边形的性质，根据正六边形性质得出作法是解题关键.22．校运会期间，小捷同学积极参与各项活动．在铅球项目中，他掷出的铅球在场地上压出一个小坑(图示是其主视图)，经测量，其中坑宽AB为8cm，小坑的最大深度为2cm，请帮助小捷同学计算铅球的半径OA 的长为多少？【答案】5cm【解析】【分析】先根据垂径定理求出AD 的长，设OA=rcm ，则OD=(r-2)cm ，再根据勾股定理求出r 的值即可．【详解】解:作OD ⊥AB 于D ，如图所示:∵AB=8cm ，OD ⊥AB ，小坑的最大深度为2cm ，∴AD=AB=4cm ． 设OA=rcm ，则OD=(r-2)cm在Rt △OAD 中，∵OA 2=OD 2+AD 2，即r 2=(r-2)2+42，解得r=5cm;即铅球的半径OA 的长为5cm ．【点评】本题考查的是垂径定理的应用，熟知平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧是解答此题的关键．23．如图，P 是⊙O 外一点，P A 是⊙O 的切线，A 是切点，B 是⊙O 上一点，且P A ＝PB ，延长BO 分别与⊙O 、切线P A 相交于C 、Q 两点．(1)求证:PB 是⊙O 的切线;(2)QD 为PB 边上的中线，若AQ ＝4，CQ ＝2，求QD 的值．12【答案】(1)详见解析;(2)QD【解析】【分析】(1)要证明PB 是⊙O 的切线，只要证明∠PBO=90°即可，根据题意可以证明△OBP ≌△OAP ，从而可以解答本题;(2)根据题意和勾股定理的知识，可以求得QD 的值．【详解】(1)证明:连接OA ，在△OBP 和△OAP 中，，∴△OBP ≌△OAP (SSS )，∴∠OBP ＝∠OAP ，∵P A 是⊙O 的切线，A 是切点，∴∠OAP ＝90°，∴∠OBP ＝90°，∵OB 是半径，∴PB 是⊙O 的切线;(2)连接OCPA PB OB OAOP OP ⎧⎪⎨⎪⎩＝＝＝∵AQ＝4，CQ＝2，∠OAQ＝90°，设OA＝r，则r2+42＝(r+2)2，解得，r＝3，则OA＝3，BC＝6，设BP＝x，则AP＝x，∵PB是圆O的切线，∴∠PBQ＝90°，∴x2+(6+2)2＝(x+4)2，解得，x＝6，∴BP＝6，∴BD＝3，∴QD，即QD【点评】本题考查切线的判定与性质，解题关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．24．如图，的直径垂直弦于，且是半径的中点，，求直径的长．【解析】【分析】连接OC ，根据垂径定理可求CM =DM =4cm ，再运用勾股定理可求半径OC ，则直径AB 可求．【详解】连接OC ．设圆的半径是r ．∵直径AB ⊥CD，∴CM =DM =CD =4cm ． ∵M 是OB 的中点，∴OM =r ，由勾股定理得:OC 2=OM 2+CM 2，∴r 2=(r )2+42，解得:r =，则直径AB =2r =(cm )．【点评】本题考查了垂径定理，解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里，运用勾股定理求解．25．如图，四边形内接于，为的直径，点为的中点．若，求的度数． O AB CD M M OB 8CD cm =AB 1212123ABCD O AB O C BD 40A ∠=B ∠【答案】.【解析】【分析】连接AC ，根据圆周角定理可得∠ACB=90°，∠BAC=∠BAD ，然后根据∠B 与∠BAC 互余即可求解.【详解】解:连接，∵是直径，∴，∵点为的中点，，∴， ∴在中，．【点评】本题主要考查圆周角定理:在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．26．如图是破残的圆形轮片，求作此残片所在的圆．(不写作法，保留作图痕迹)【答案】见解析70B ∠=12AC AB 90ACB ∠=C BD 40BAD ∠=11402022BAC BAD ∠=∠=⨯=Rt ABC 902070B ∠=-=【解析】【分析】根据圆的性质，弦的垂直平分线过圆心，所以只要找到两条弦的垂直平分线，交点即为圆心，有圆心就可以作出圆轮．【详解】如图:圆O为所求．【点评】本题考查了圆的基本性质，是一种求圆心的作法．作圆的方法有:①圆心半径;②三个圆上的点．。

人教版数学六年级上册第五单元《圆》单元测试卷学校:___________姓名：___________班级：___________考号：___________一、选择题1．用40厘米长的铁丝分别围成长方形、正方形、圆，（）的面积最大。

A．长方形B．正方形C．圆2．如图，阴影部分的周长是（）cm．A．π B．2πC．4π D．2.5π3．半径是一条（）．A．线段B．射线C．直线4．圆是平面上的（）。

A．直线图形B．曲线图形C．无法确定5．如图，图形（单位：分米）涂色部分的面积是（）。

A．12.84dm²B．9.24dm²C．18.24dm²D．9.42dm²6．一个圆的直径增加2倍后，面积是原来的（）A．9倍B．8倍C．4倍D．2倍7．把完全相同的两个半圆合成一个整圆后，它们的（）A．面积不变，周长减少了B．面积增加了，周长不变C．面积不变，周长增加了D．面积和周长都减少了8．在面积相等的情况下，正方形、长方形和圆三个图形相比，周长最短的是（）．A．长方形B．正方形C．圆二、判断题9．在同一个圆中，两条半径就是一条直径。

（________）10．顶点在圆内的角一定是圆心角．（____）11．所有圆的周长和它的直径的比值一定相等。

（________）12．半径是2厘米的圆的周长和面积相等。

（________）13．大小两个不同的圆，它们的圆周率也不同。

（________）14．圆在平面滚动时，圆心在一条直线上运动．（_____）15．两个圆的周长相等，这两个圆的直径也一定相等（_____）16．扇形的大小只与它的圆心角的度数有关。

（________）三、填空题17．______和经过______两端的______所围成的图形叫做扇形．18．用圆规画出圆以后，针尖固定的一点就是________，通常用字母________表示，________决定圆的位置。

19．看图填空（单位：厘米）．图1：d=（_____）cm 图2：d=（_____）cm 图3：r=（_____）cm 图4：d=（_____）cm20．一个圆形的笔筒的半径是8厘米，它的直径是（________）厘米，周长是（________）厘米。

人教版六年级上册数学第五单元《圆》测试卷一.选择题(共6题，共12分)1.要画直径4厘米的圆，圆规两脚之间的距离就是（）厘米。

A.4B.2C.82.画一个周长是18.84厘米的圆，圆规的两脚之间的距离应该是（）厘米。

A.3B.6C.93.小红用彩色纸剪了一个半圆（如图），半径是6cm，求周长，列式是（）。

A.3.14×6×2÷2B.3.14×6×2÷2+6C.3.14×6×2÷2+6×24.圆面积扩大16倍,则周长随着扩大（）。

A.16倍B.32倍C.4倍5.把一根长10米的铜丝，在一个圆盘上绕了3圈，还多0.58米，这个圆盘的半径是（）米。

A.0.5B.1C.1.56.从圆心开始，把一个圆平均分成若干份，剪开后可以拼成的图形是（）。

A.三角形B.长方形C.梯形二.判断题(共6题，共12分)1.圆的任何一条直径都是圆的对称轴，所以圆有无数条对称轴。

（）2.圆的周长和直径越大，圆周率就越大。

（）3.两条半径就是一条直径。

（）4.画圆时，圆规两脚间的距离就是圆的直径。

（）5.在同一个圆中，圆心到圆上的距离处处相等。

（）6.半圆形的周长是圆周长的一半。

（）三.填空题(共6题，共12分)1.扇形是（）图形，它有（）条对称轴。

2.画一个直径为4厘米的圆，圆规两脚间的距离应该是（）。

3.一个圆形的笔筒的半径是8厘米，它的直径是（）厘米，周长是（）厘米。

4.画一个直径是5厘米的圆，圆规两脚之间的距离是（）厘米。

如果要画一个周长是12.56厘米的圆，圆规两脚之间的距离应该是（）厘米，这个圆的面积是（）平方厘米。

5.一个圆形粮仓的半径是3米，它的直径是（）厘米，周长是（）厘米。

6.要画一个半径为4厘米的圆，圆规的两脚应叉开（）厘米；要画一个周长是18.84厘米的圆，圆规的两脚应叉开（）厘米。

四.计算题(共1题，共6分)1.求下面图形的周长。

故选D．
[点睛]本题考查了垂径定理、勾股定理的应用,关键在于正确地作出辅助线构建直角三角形,认真地进行计算．
5.如图,A B是⊙O的弦,点C在圆上,已知∠OB A＝40°,则∠C＝()
A. 40°B. 50°C. 60°D. 80°
[答案]B
[解析]
[分析]
首先根据等边对等角即可求得 的度数,然后根据三角形的内角和定理求得 的度数,再根据圆周角定理即可求解.
[答案]相离
[解析]
[分析]
A. B. C. D.
[答案]D
[解析]
[分析]
连接OA,由题意即可得出OC、OA的长度,运用勾股定理即可推出A D的长度,然后,通过垂径定理即可推出A B的长度．
[详解]连接OA．
∵⊙O的弦A B垂直平分半径OC,C D= ,∴OC= ,∴OA= ．
∵OC⊥A B,∴A D= ．
∵A B=2A D,∴A B= ．
1.下列关于圆的说法,不正确的是（ ）
A.圆是轴对称图形B.圆是中心对称图形
C.优弧大于劣弧D.垂直于弦的直径平分这条弦所对的弧
[答案]C
[解析]
[分析]
根据圆的基本概念、圆的基本性质分析即可．
[详解]A．圆是轴对称图形,过圆心的直线都是它的对称轴,该说法正确；
B．圆是中心对称图形,它的中心对称点为圆心,该说法正确；
[详解] ,
,
,
.
故选： .
[点睛]本题考查了等腰三角形的性质定理以及圆周角定理,正确理解定理是关键.
6.如图,现有一个圆心角为90°,半径为8Cm的扇形纸片,用它恰好围成一个圆锥的侧面（接缝忽略不计）,则该圆锥底面圆的半径为（）
A.2CmB.3CmC.4CmD.1Cm

小学人教版六年级数学上册第五单元《圆》单元测试卷姓名等级一、选择题1．在长10厘米，宽8厘米的铁皮里剪一个最大的圆，圆的直径是（）A．10 cm B．5 cm C．16 cm D．8 cm2．如图（单位：厘米）阴影部分的周长是（）A．38.84B．57.68C．42.84D．18.843．两个圆的直径比是3:1，它们的周长比是（）。

A．3:1B．1:3C．9:14．把一个圆平均分成10个扇形,圆心角都是( )．A．90°B．36°C．18°D．70°5．大小两个圆的半径之比是3：1，则它们的面积之比是（）A．3：1B．6：1C．9：1D．9：26．在长8cm，宽6cm的长方形内，剪一个最大的圆，那么圆的周长是（）cm。

A．25.12B．28.26C．18.84D．50.247．从中午12点到下午3点，时钟上长度为5cm的时针尖端走过了( )cm。

A．7.85B．15.7C．31.4D．62.88．用放大镜放大一段弧时，不能被放大的部分是（）A．圆心角 B．半径 C．弧长 D．都能放大9．在一个长6厘米、宽4厘米的长方形中画一个最大的圆，这个圆的（）厘米。

A．直径是6B．半径是6C．直径是4D．半径是4 10．两个圆的周长比是4：9，这两个圆的面积比是（）A．4：9B．2：3C．16：81D．9：4二、填空题1．一个圆的周长是188.4分米，这个圆的半径是( )分米，面积是( )平方分米．2．两个圆直径的比是4∶3，那么这两个圆半径的比是（）。

3．一个圆的半径是 3 厘米，这个圆的面积是（）平方厘米。

4．圆有无数条半径，所有的半径都( )。

5．在边长为5厘米的正方形中剪下一个最大的圆，圆的周长是( )厘米。

6．如图是一个边长为4厘米的正方形，则阴影部分的面积是( )平方厘米。

7．一个圆的面积是以这个圆的半径为边长的一个正方形的面积的( )倍．18．圆的周长是直径的( )倍，周长除以直径的商叫做( )，通常取( )。

A.5B.6C.7D.8
3. 如图，圆O是△ABC的外接圆，∠A＝68°，则∠OBC的大小是( )
A 22°B. 26°C. 32°D. 68°
4.若⊙O的面积为25π，在同一平面内有一个点P，且点P到圆心O的距离为4.9，则点P与⊙O的位置关系为( )
A.点P在⊙O外B.点P在⊙O上
C.点P ⊙O内D.无法确定
点睛：本题考查了切线的性质、等腰三角形的性质以及勾股定理的运用，熟记切线的性质定理是解题的关键．
11.如图，已知一块圆心角为270°的扇形铁皮，用它作一个圆锥形的烟囱帽（接缝忽略不计），圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是( )
A.40cmB.50cmC.60cmD.80cm
【答案】A
(2)△PCF是等腰三角形．
26.如图，在直角坐标系中，⊙M经过原点O(0，0)，点A( ，0)与点B(0，－ )，点D在劣弧 上，连结BD交x轴于点C，且∠COD＝∠CBO.
(1)求⊙M的半径；
(2)求证：BD平分∠ABO；
(3)在线段BD的延长线上找一点E，使得直线AE恰为⊙M的切线，求此时点E的坐标．
A. 5 B. 5 C. 5D.
【答案】A
【解析】
解：过点D作OD⊥AC于点D，∵AB是⊙O的直径，PA切⊙O于点A，∴AB⊥AP，∴∠BAP=90°，∵∠P=30°，∴∠AOP=60°，∴∠AOC=120°，∵OA=OC，∴∠OAD=30°，∵AB=10，∴OA=5，∴OD= AO=2.5，∴AD= = ，∴AC=2AD= ，故选A．
人教版数学九年级上学期
《圆》单元测试
（满分120分，考试用时120分钟）
一、选择题
1.下列说法中不正确的是( )
A.圆是对称图形B.三点确定一个圆

圆第一单元测试卷一、选择题（每题3分，共30分）1. 圆的周长公式是（）。

A. C = 2πrB. C = πdC. C = 4rD. C = 2d2. 半径为3的圆的面积是（）。

A. 28.26B. 9C. 18.84D. 363. 圆的直径是半径的（）倍。

A. 1B. 2C. 4D. 34. 一个圆的半径增加1厘米，面积增加（）。

A. πB. 2πC. π(2r+1)D. π(r+1)²5. 扇形的面积公式是（）。

A. S = 1/2 * r² * θB. S = 1/2 * r * θC. S = r * θD. S = π * r²6. 圆的内接四边形的对角和是（）。

A. 90°B. 180°C. 360°D. 270°7. 圆的切线与半径垂直，垂直点在（）。

A. 圆心B. 圆周上C. 圆内D. 圆外8. 圆的弧长公式是（）。

A. L = r * θB. L = 2πr * θ/360C. L = πr * θD. L = r * θ/29. 圆的内切圆与外切圆的半径之和等于（）。

A. 内切圆半径B. 外切圆半径C. 圆的直径D. 圆的半径10. 圆的内接多边形的边数增加，其内角趋近于（）。

A. 90°B. 180°C. 360°D. 无法确定二、填空题（每题2分，共20分）11. 半径为5的圆的周长是______。

12. 圆的面积公式是S = ______。

13. 扇形的弧长是半径的2倍时，其圆心角是______度。

14. 圆的切线与半径垂直，其切线长度等于______。

15. 圆的内接正六边形的边长等于______。

16. 圆的直径为10，其内接正方形的面积是______。

17. 圆的半径为r，圆心角为α，扇形的面积是______。

18. 圆的内接正三角形的边长为s，其半径为______。