实验八 验证距离平方反比率
- 格式:doc
- 大小:128.00 KB
- 文档页数:5

牛顿引力平方反比定律的发现万有引力定律发现是人类认识史上最重大的事件之一。
国内外科学史界一致公认,在这一发现过程中,牛顿对引力平方反比定律的发现,即所谓“开普勒命题”的证明,起到了关键性作用,它标志着牛顿成熟地掌握了动力学原理,是牛顿在1685至1686年间发现万有引力定律的必要前提。
牛顿在一份约写于1717年的自传体备忘录中,就弓!力平方反比定律的发现曾指出,他是在1666年根据开普勒行星运动周期定律“推出了”力的平方反比关系,未提及人们通常一认为的另一根据一—离心力定律,并认为:“惠更斯先生后来所发表的离心力的理论我相信是在我之前的。
最后,在1676和1677年之间的冬季,我发现了一个命题,那就是在离心力等于和距离的平方成反比的情况下,一个行星必然要统处于椭圆下面一个脐点(即焦点一笔者注)的力心作椭圆运动,同时那画向这个中心的半径所掠过的面积,其大小和所用的时间成正比。
在1683和1684年之间的冬季,这个命题及其论证也写进了皇家学会的记事册。
”牛顿在论及开普勒命题的一份来发表手稿中写道:“在1677年,我应用流数的反求法(即积分一笔者注),发现了开普勒天文学命题的证明,那就是《原理》第一卷的命题Ⅺ:行星在椭圆轨道上运动。
”他在其后追加的一页草稿中又把“证明”的日期“推迟”到1679午。
事实上,《原理》第一卷命题Ⅺ,即开普勒命题的内容是:物体沿椭圆绕转,求指向椭圆焦点的向心力定律;而牛顿有关开普勒命题的论证,是1685年2月13日前不久才写进皇家学会的记事册。
因此,从牛顿晚年因微积分发明权之争而撰造的“剧情说明式的”自述中,我们无法确定牛顿在何时证明了开普勒命题,其对平方反比定律的认识过程,也与史实有出入。
国外史学界认为,牛顿是在17世纪60年代,应用离心力定律和开普勒周期定律,得到圆轨道上的引力平方反比关系,而论及椭圆轨道上引力与距离关系的开普勒命题,是在1679年或1684年得到证明的。

简介电的平方反比定律指出,电场强度与离源的距离的平方成反比。
这一定律是由亨利-卡文迪什于1776年首次提出的,此后一直在实验中得到验证。
这篇文章将讨论平方反比定律的历史,它的数学表述,以及它的实验验证。
平方反比定律的历史反平方律是由亨利-卡文迪许在1776年首次提出的。
他提出,当两个电荷相隔一定距离时,它们的相互作用遵循反平方律。
这意味着,如果一个电荷增加一倍,那么它们之间的力将减少到原来的四分之一。
卡文迪许的工作为理解电场如何相互作用以及它们如何与物质相互作用奠定了基础。
1820年,迈克尔-法拉第进一步发展了卡文迪许的工作,并提出电场在空气或水等介质中传播时服从反平方律。
法拉第的工作使人们对电场如何与物质相互作用有了更全面的了解,并有助于建立对电的现代理解。
平方反比定律的数学表述平方反比定律的数学表述是:如果两个电荷q_1和q_2相隔一段距离,那么它们的相互作用就遵循平方反比定律。
F = frac{q_1q_2}{4\pi\epsilon_0r^2}。
其中F是它们之间的力,q_1和q_2是它们各自的电荷,epsilon_0是自由空间的引力(8.854 x 10^{-12} C^2/Nm^2),r是它们的分离距离。
这个方程可以用来计算任何给定距离的两个电荷之间的力。
平方反比定律的实验验证自从卡文迪许在1776年首次提出平方反比定律以来,它已经在实验中得到验证。
验证这一定律的最常用方法是测量两个带电物体之间的力与它们的分离距离的函数关系。
这可以通过一个被称为静电天平的仪器来完成,该仪器使用弹簧秤或其他力传感器测量两个带电物体在不同距离上的力。
通过测量不同距离的这些力,有可能确定它们是否如理论所预测的那样服从反平方关系。
除了使用静电平衡来验证这一定律外,还可以使用库仑定律来验证,库仑定律指出。
F=frac{kq_1q_2}{r^2}。
其中k是库仑常数(8.99 x 10^9 Nm^2/C^2)。
通过使用库仑定律测量不同距离的两个带电物体之间的力,可以验证它们是否如理论所预测的那样服从反平方关系。
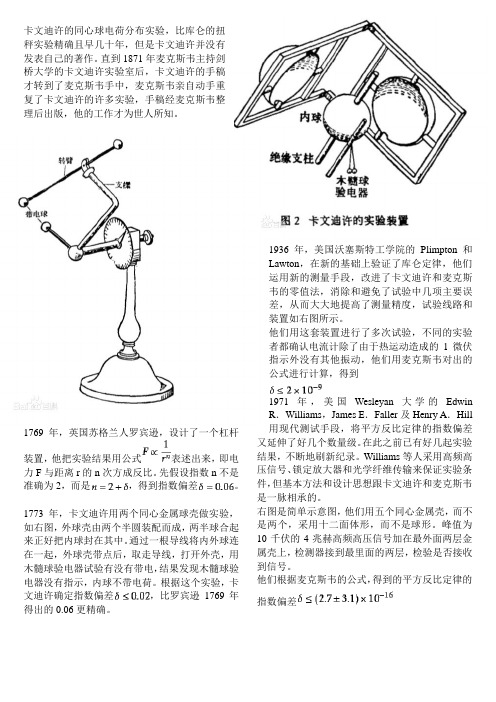
卡文迪许的同心球电荷分布实验,比库仑的扭秤实验精确且早几十年,但是卡文迪许并没有发表自己的著作。
直到1871年麦克斯韦主持剑桥大学的卡文迪许实验室后,卡文迪许的手稿才转到了麦克斯韦手中,麦克斯韦亲自动手重复了卡文迪许的许多实验,手稿经麦克斯韦整理后出版,他的工作才为世人所知。
1769年,英国苏格兰人罗宾逊,设计了一个杠杆装置,他把实验结果用公式表述出来,即电力F与距离r的n次方成反比。
先假设指数n不是准确为2,而是,得到指数偏差。
1773年,卡文迪许用两个同心金属球壳做实验,如右图,外球壳由两个半圆装配而成,两半球合起来正好把内球封在其中。
通过一根导线将内外球连在一起,外球壳带点后,取走导线,打开外壳,用木髓球验电器试验有没有带电,结果发现木髓球验电器没有指示,内球不带电荷。
根据这个实验,卡文迪许确定指数偏差,比罗宾逊1769年得出的0.06更精确。
1936年,美国沃塞斯特工学院的Plimpton和Lawton,在新的基础上验证了库仑定律,他们运用新的测量手段,改进了卡文迪许和麦克斯韦的零值法,消除和避免了试验中几项主要误差,从而大大地提高了测量精度,试验线路和装置如右图所示。
他们用这套装置进行了多次试验,不同的实验者都确认电流计除了由于热运动造成的1微伏指示外没有其他振动,他们用麦克斯韦对出的公式进行计算,得到1971年,美国Wesleyan大学的Edwin R.Williams,James E.Faller及Henry A.Hill 用现代测试手段,将平方反比定律的指数偏差又延伸了好几个数量级。
在此之前已有好几起实验结果,不断地刷新纪录。
Williams等人采用高频高压信号、锁定放大器和光学纤维传输来保证实验条件,但基本方法和设计思想跟卡文迪许和麦克斯韦是一脉相承的。
右图是简单示意图,他们用五个同心金属壳,而不是两个,采用十二面体形,而不是球形。
峰值为10千伏的4兆赫高频高压信号加在最外面两层金属壳上,检测器接到最里面的两层,检验是否接收到信号。

卡文迪许的同心球电荷分布实验,比库仑的扭秤实验精确且早几十年,但是卡文迪许并没有发表自己的著作。
直到1871年麦克斯韦主持剑桥大学的卡文迪许实验室后,卡文迪许的手稿才转到了麦克斯韦手中,麦克斯韦亲自动手重复了卡文迪许的许多实验,手稿经麦克斯韦整理后出版,他的工作才为世人所知。
1769年,英国苏格兰人罗宾逊,设计了一个杠杆装置,他把实验结果用公式表述出来,即电力F与距离r的n次方成反比。
先假设指数n不是准确为2,而是,得到指数偏差。
1773年,卡文迪许用两个同心金属球壳做实验,如右图,外球壳由两个半圆装配而成,两半球合起来正好把内球封在其中。
通过一根导线将内外球连在一起,外球壳带点后,取走导线,打开外壳,用木髓球验电器试验有没有带电,结果发现木髓球验电器没有指示,内球不带电荷。
根据这个实验,卡文迪许确定指数偏差,比罗宾逊1769年得出的0.06更精确。
1936年,美国沃塞斯特工学院的Plimpton和Lawton,在新的基础上验证了库仑定律,他们运用新的测量手段,改进了卡文迪许和麦克斯韦的零值法,消除和避免了试验中几项主要误差,从而大大地提高了测量精度,试验线路和装置如右图所示。
他们用这套装置进行了多次试验,不同的实验者都确认电流计除了由于热运动造成的1微伏指示外没有其他振动,他们用麦克斯韦对出的公式进行计算,得到1971年,美国Wesleyan大学的Edwin R.Williams,James E.Faller及Henry A.Hill 用现代测试手段,将平方反比定律的指数偏差又延伸了好几个数量级。
在此之前已有好几起实验结果,不断地刷新纪录。
Williams等人采用高频高压信号、锁定放大器和光学纤维传输来保证实验条件,但基本方法和设计思想跟卡文迪许和麦克斯韦是一脉相承的。
右图是简单示意图,他们用五个同心金属壳,而不是两个,采用十二面体形,而不是球形。
峰值为10千伏的4兆赫高频高压信号加在最外面两层金属壳上,检测器接到最里面的两层,检验是否接收到信号。


牛顿巧证平方反比-概述说明以及解释1.引言1.1 概述:牛顿巧证平方反比是牛顿在物理学领域所作出的重要贡献之一。
通过对重力现象的深入研究和实验,牛顿发现了物体间的引力与它们之间的距离的平方成反比的关系,即平方反比定律。
这一发现不仅在当时引起了轰动,也为后世的物理学发展奠定了基础。
本文将对牛顿的生平背景、平方反比定律的提出及其实验与证明进行探讨,在深入分析牛顿巧证平方反比的意义和他在科学上的重要贡献的基础上,对这一重要发现进行全面的论述和解析。
1.2 文章结构在本文中,我们将通过三个主要部分来探讨牛顿巧证平方反比的相关内容。
首先,在第二部分中,我们会介绍牛顿的生平背景,了解他在科学领域的成就和影响。
接着,我们将详细讨论平方反比定律的提出,探讨牛顿是如何得出这一定律的。
最后,我们会深入研究实验与证明的过程,揭示牛顿是如何通过实践验证这一定律的正确性。
通过这些内容的呈现,我们希望能全面了解牛顿巧证平方反比的意义以及他对科学领域所做出的不可磨灭的贡献。
文章1.3 目的:本文旨在探讨牛顿巧证平方反比定律的过程和意义,通过介绍牛顿的生平背景、平方反比定律的提出以及实验与证明的过程,分析牛顿在科学领域的贡献和他对物理学的重大影响。
通过对这一重要科学定律的深入研究,可以更好地理解牛顿的思想和方法,同时也可以体会到科学研究中的创新与突破。
探讨牛顿巧证平方反比的意义,可以帮助我们更全面地认识和理解自然界的规律,感受到科学探索的魅力和价值。
最终,希望通过本文的撰写,让读者更加深入地了解牛顿的科学思想,激发大家对科学研究的兴趣和热情。
2.正文2.1 牛顿的生平背景艾萨克·牛顿(Isaac Newton,1643年12月25日-1727年3月20日)是英国著名的物理学家、数学家和天文学家,也是科学史上最重要的人物之一。
他出生在英格兰的林肯郡,父母早逝,由祖母抚养长大。
牛顿在青少年时代表现出非凡的数学天赋,但由于家庭贫困,他无法接受正规的教育,只能在家自学。
探究光强变化和距离之间关系的实验装置设计与制作问题的提出:传统实验方法:1、在一条直线一端设置一个光源(小灯泡等)2、用光强传感器在直线上距离光源最近点测量光源光强,每测量一次,就以适当的单位距离向直线上远离光源移动一个单位距离,重复进行以上步骤,并记录数据3、计算,制图表其中存在问题:1、在开放,有外界光环境中进行实验,外界光会对光强传感器产生干扰2、人工操作,进行计算制图表,程序复杂,容易增大误差,费时费力我的改进实验设计:(实验材料:水箱1个,220v潜水泵1个,泡沫板【或浮板】1块,小灯泡1个,电源+开关1套,亮度传感器1个,超声波距离传感器1个,数据采集器【或电脑】1个)1、用水代替空气作为光的传播介质2、用超声波距离传感器直接测量传感器与光源距离3、利用水箱中水位的匀速上升带动光强传感器上升,代替人工移动4、利用PASCO传感器-数据采集器系统和计算机采集数据,计算制图表,拟合设计与制作实验设备:1、用有机玻璃制作顶部开发的水箱,并用黑漆喷涂全身,在底部中央留有一个1cm*1cm的透光口2、按水箱内部底面积裁制一块轻质塑料板,全身喷涂黑漆。
放于水箱底部,在水箱透光口位置钻一个安装光强传感器的圆孔,底部粘上能使塑料板及光强传感器浮于水面,足够体积的泡沫塑料,并空出中央部分组装实验设备:1、按照光源高度垫高水箱(在保证水箱稳定的前提下),在底部放置一个光源,对准透光口位置2、在浮板上安装光强传感器,将浮板放与水箱底部3、在铁架台上安装超声波距离传感器,使超声波距离传感器位于水箱上方,与浮板平行4、设置好输水管和水泵5、将传感器与数据采集器、计算机连接好使用装置进行实验:1、开启各部分电源2、开始采集数据,水泵开始工作,水位缓缓上升3、水位接近水箱顶部,水泵停止工作4、计算机绘制图表,进行数据拟合改进后实验装置的特点:1、在隔绝外界光的环境中进行实验,减少外界光对光强传感器的干扰2、全过程自动进行,效率高,误差小3、计算机自动采集数据、分析、绘制图表、拟合改进实验装置2:(实验材料:水箱1个,直尺一把,220v潜水泵1个,泡沫板【或浮板】1块,小灯泡1个,电源+开关1套,手机2个【带摄像头】,电脑1台)1、用水代替空气作为光的传播介质2、用手机计时器间接测量传感器向光源不同距离的时刻3、利用水箱中水位的匀速上升带动光强传感器上升,代替人工移动4、利用手机摄像头拍摄灯泡亮度变化的连续视频制作实验设备:1、用有机玻璃制作顶部开发的水箱,并用黑漆喷涂全身,在底部中央留有一个1cm*1cm的透光口2、按水箱内部底面积裁制一块轻质塑料板,全身喷涂黑漆。
实验2:验证距离平方反比率实验目的1. 学会根据实验精度要求选择测量时间。
2. 学会运用现行最小二乘法拟合实验数据,验证距离平方反比律。
内容1. 改变探测器与放射源之间的距离,测量各相应位置的计数率,获取一定精度要求的实验数据。
2. 用等精度线性最小二乘法处理实验数据,验证γ射线强度随距离的变化规律-平方反比律。
原理在放射性测量中,为得到一定精度的实验数据,必须根据放射源及本底计数率的实际情况,结合某些客观条件(如探测器效率及测量时间的限制),确定适当的测量方案;为了得到可靠的实验结果,还需要进行数据分析和处理。
我们将通过本实验作有关的基本训练。
1.γ射线强度随距离的变化关系——平方反比律设有一点源(指源的线度与源到观察点的距离相比很小),向各方向均匀地发射γ光子。
若单位时间发射的光子数为0N ,则在以点源为球心,以R 为半径的球面上,单位时间内将有0N 个光子穿过(设空间内无辐射之吸收与散射等)。
因此,在离源R 处,单位时间、单位面积上通过的γ光子数为:2204RCR N I ==π ( 1 )(1)式中,π40N C =,对于一定活度的源,C 是常数。
可见21RI ∝,此即距离平方反比律。
显然,若在测量中,探测器的灵敏体积始终位于源对探测器所张的立体角内时,测得的净计数率n 也应与2R 成反比。
即有2'RC n = ( 2)(2)式中'C 为常数。
因此,验证平方反比律的问题在实验上就归结为测量n 与R 的关系。
怎样才能在一定的实验条件下,在规定的实验时间内,取得满足精度要求的数据呢?下面就此进行讨论。
2. 按照实验精度要求合理分配计数时间在每次测量的计数中都包括有本底计数,而且在本实验中,随着距离R 的不同本底计数在测量的计数中占的比例也不同。
设在s t 时间内测得源加本底的总计数为s N ;在b t 时间内测得本底计数为b N ,则源的净计数n 为:bbs s b s t N t N n n n -=-=( 3 )总计数率s n 与本底计数率b n 的标准误差分别为b s σσ,:sss s s t N t N ==σ (4 )bb bbb t n t N ==σ( 5 )根据误差传递公式,净计数率n 的标准误差n σ及相对误差n ν分别为:212122)()(bbs s bs n t n t n +=+=σσσ ( 6 ))/()(21b s bb s s nn n n t n t n n -+==σν( 7 )因此,净计数率的结果可表示为:21)()(bb s s b s n t n t n n n n +±-=±σ ( 8 )或 )]/()(1)[()1(21b s bb s s b s n n n t n t n n n n -+±-=±ν ( 9 )为了减少n 的误差,应增加s t 与b t 。
光学距离平方反比定律光学距离平方反比定律,这听起来是不是有点深奥呢?别急,咱们慢慢聊聊。
想象一下,你在一个阳光明媚的日子里,和朋友在公园里打球,突然,你发现那球在阳光下的影子变得越来越小。
没错,这就是光的神奇之处!光源越远,光的强度就越弱,这就像你和朋友的声音一样,离得越远,听得越模糊。
光学距离平方反比定律就是告诉我们,光的强度和距离之间的关系,就像“远水不救近火”一样,越远的东西,越难得到。
咱们再来想象一下,如果有一天,你站在一个巨大的舞台上,四周都是观众。
你发觉,靠近舞台的人听得特别清楚,后面的人却得屏息才能听见。
这就是光线的工作原理。
光从灯光射出,随着距离的增加,光的强度就像是“人往高处走”,往后退的观众,越听越模糊。
你会发现,光的强度和距离是成反比的关系,远离光源,光的强度就会迅速下降,就像一瓶汽水打开后,气泡一溜烟儿跑掉,喝到最后只剩下水了,没意思吧。
光的传播就像是咱们生活中的一些事情,近在咫尺的东西总是最清晰的。
比如,早上起床的时候,阳光透过窗帘洒进来,房间里亮堂堂的,特别舒服。
但要是你站在窗外,哎呀,那光照得你眼睛发疼,想要遮挡都来不及。
这时候你就明白了,光的强度在靠近的时候最强,离得远了就像是远方的亲戚,虽然偶尔想念,但见面没那么容易。
咱们还可以用“细水长流”来形容光的强度。
光的强度就像涓涓细流,源源不断,但如果你把它放在一个大池子里,随着距离的增加,水流就变得越来越小。
这就是光的本质,随着你离光源的距离增大,光的强度就会越来越弱,让你不得不承认,距离产生的不是美,而是模糊。
其实这道理在生活中无处不在,像有些朋友,平时聊得热火朝天,距离一旦拉开,连问候都成了奢侈。
然后,再来看看实际的应用。
科学家们可真是聪明,他们把这个光学定律运用到了许多地方。
比如在天文观察中,遥远的星星发出的光,随着距离的增加,强度变弱,结果我们看到的星星只是一闪而过的光点。
就像那句“路遥知马力”,越远的星星,越能考验你对光的理解。
实验八 验证距离平方反比率
一、 实验目的:
1. 学会根据实验精度要求选择测量时间和测量次数;
2. 学会用线性最小二乘法拟合实验数据;
3. 理解距离平方反比率的意义和实际指导作用。
二、 实验器材:
1、 γ总量检测仪(KZG03C 辐射总量检测仪);
2、 Cs-137点源一个;
3、 铅准直器、铅皮套和铅板若干。
三、 实验原理:
设有一点源向各个方向均匀地发射光子(γ光子),若单位时间发射的光子数为N 0 ,测量以点源为球心、以R 为半径的球面上,单位时间将有N 0 个光子穿过(假设空间无辐射、吸收与散射等作用—理想条件),因此在离源R 处单位时间单位面积上通过的γ光子数为:
02
4N
I R
π=
---------------------------------------------- (1)
令04N C
π
=
,当放射源的强度I 一定时,则C 为常数,但是通常情况下
源在不停的衰变,因此N 0 也随时在变小,故我们在做实验时一般视很短时间内N 0不变。
所以可得以下公式:
2
C I R
=
⇒ I ∝
2
1R
四、 实验步骤:
1、 由指导老师或自己在实验场所及附近设定一条测线进行不同
测点放射性γ总量测量。
每隔10秒记数,每一个测量点记数3次取均值。
2、在实验室内找一定点,在同一条件下进行多次重复性测量(每
隔10秒记一次数,不少于100次),然后以平均值N为中心,以δ∕2为组距统计画出落在计数落在N±δ、N±2δ、N±3δ区间内的概率,与理论值相比较。
(δ为均方差)
五、数据分析与处理:
1.不同地点测量结果:
表1 测量的原始数据
根据表1测得的数据在平面直角坐标上画出测线的放射性水平示意图(注:用测点表示横坐标,测点间距要求大体一致;用每个测点的计数表示纵坐标)。
2.固定地点测量结果:
表2测量的原始数据
例图1
计数落在N±δ区间内的概率为84%,落在N±2δ区间内的概率为94%,落在N±3δ区间内的概率为98%,基本符合正态分布。
例图2
六、实验结论与心得体会:
七、思考题:
1、衰变服从什么规律,核辐射测量的两个基本特征是什么?
2、统计误差的意义是什么?
八、参考文献:
1.复旦大学、清华大学、北京大学合编《原子核物理实验方法》
原子能出版社1998;
2.[美] 格伦F.诺尔《辐射探测与测量》原子能出版社1988;
3.贾文懿《核地球物理仪器》原子能出版社1982;
4.周容生《核方法原理及应用》地质出版社1994。