5.6向心加速度

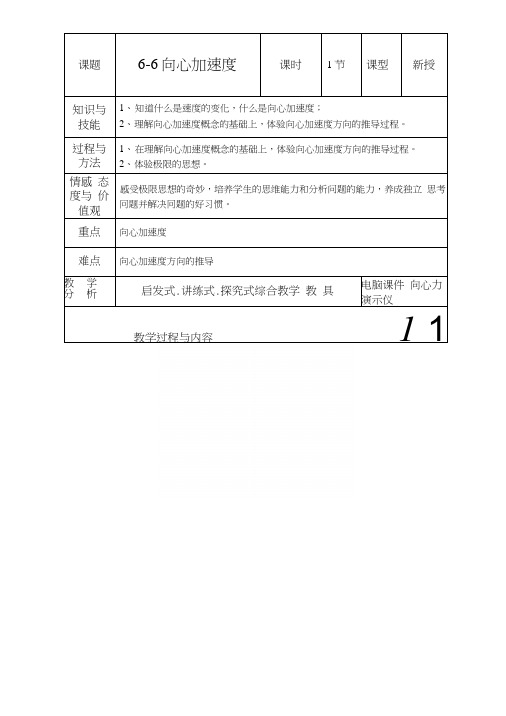
课题6-6向心加速度课时 1节 课型 新授知识与 技能 1、知道什么是速度的变化，什么是向心加速度； 2、理解向心加速度概念的基础上，体验向心加速度方向的推导过程。

过程与 方法 1、 在理解向心加速度概念的基础上，体验向心加速度方向的推导过程。

2、 体验极限的思想。

情感 态度与 价值观 感受极限思想的奇妙，培养学生的思维能力和分析问题的能力，养成独立 思考冋题并解决冋题的好习惯。

重点 向心加速度难点向心加速度方向的推导学析教分启发式.讲练式.探究式综合教学 教 具电脑课件 向心力演示仪教学过程与内容1 1思考与讨论：我们已经知道，如果物体不受力，它将作匀速直线运动。

我们还知道，力的作用效果之一是改变物体的运动状态，即改变物体速度的大小或（和）方向。

所以沿着圆周运动的物体一定受力。

那么，作匀速圆周运动的物体体，它所受的力沿着什么方向？下面我们来考虑几个实例会受到启发。

实例1:地球绕太阳的运动近似为匀速圆周运动，地球受到什么力的作用？这个力可能沿着什么方向？实例2:光滑的水平桌面上一个小球由于细线的牵引，绕桌面上的图钉作匀速圆周运动。

小球受几个力的作用？这几个力的合力沿着什么方向？通过以上分析和学生的回答，小结：1、上述几个实例中，匀速圆周运动的物体，要受到一个指向圆心方向的力。

2、在前面学习加速度对速度的影响时，我们知道，一个加速度沿着速度方向的分量只改变速度的大小;垂直于速度方向的分量只改变速度的方向。

匀速圆周运动是速度大小不变、方向沿着圆周的切线方向的运动，所以一定受到一个垂直于切线，即指向圆心方向的加速度。

实例1、2不要求学生回答得非常准确，只是对向心加速度的方向有个直观的感受。

加速度对速度的影响时在曲线运动肘已有基础。

教学过程与内容课堂调控下面我们再从速度娈化（Av）的角度来讨论作圆周运动的物体的加速度的方向。

K做直线运动的物体：设初速度（V,）方向为正方向，末速度为巾，Av=V2-Vio例如：若物体的初速度v,=5m/s,向东；末速度v2=8m/s,也向东。

5.5 向心加速度一、教学目标1、知识与技能（1）理解速度变化量和向心加速度的概念；（2）知道向心加速度和线速度、角速度的关系式；（3）能够运用向心加速度公式求解有关问题。

2、过程与方法：体会速度变化量的处理特点，体验向心加速度的导出过程，领会推导过程中用到的数学方法，教师启发、引导，学生自主阅读、思考、讨论、交流学习成果。

3、情感、与价值观：培养学生思维能力和分析问题的能力，培养学生探究问题的热情，乐于学习的品质。

特别是“做一做”的实施，要通过教师的引导让学生体会成功的喜悦。

二、教学重点/难点教学重点：理解匀速圆周运动中加速度的产生原因，掌握向心加速度的确定方法和计算公式。

教学难点：向心加速度方向的确定过程和向心加速度公式的推导与应用。

三、教学用具多媒体、板书四、教学过程（一）新课导入思考与讨论：如果物体所受的合力为零，物体做什么运动？物体做匀速直线运动或静止做圆周运动的物体所受的合力为零吗？物体合力一定不为0，一定有加速度那么做匀速圆周运动的物体所受合外力方向有何特点，它们的加速度大小方向如何确定？通过上面的分析我们知道在现实生活中，物体都要在一定的外力作用下才能做曲线运动，如图教所示(课件展示)．地球绕太阳做(近似的)匀速圆周运动 小球绕桌面上的图钉做匀速圆周运动对于图中的地球和小球，它们受到了什么样的外力作用？它们的加速度大小和方向如何确定？一、圆周运动的向心加速度的方向(1)实例分析①地球绕太阳做近似的匀速圆周运动，地球受太阳的力是万有引力，方向由地球中心指向太阳中心．②光滑桌面上一个小球由于细线的牵引，绕桌面上的图钉做匀速圆周运动．小球受到的力有重力、桌面的支持力、细线的拉力．其中重力和支持力在竖直方向上平衡，合力总是指向圆心．(2)结论猜测一切做匀速圆周运动的物体的合力和加速度方向均指向圆心．定义：任何做匀速圆周运动的物体的加速度都指向圆心，这个加速度叫做向心加速度． 二、向心加速度的大小 思考：加速度的定义式是什么？tv a ∆∆=v ∆：速度的变化量a 的方向与Δv 的方向相同 问题：如何确定Δv 的方向? 用矢量图表示速度变化量直线运动中的速度的变化量： v1=3m/s,水平向东; v2=5m/s,水平向东. Δv = 2m/sv1=5m/s,水平向东; v2=3m/s,水平向东. Δv = -2m/s作法：从同一点作出物体在一段时间的始末两个速度矢量v1和v2，从初速度v1的末端至末速度v2的末端所作的矢量就是速度的变化量△v向心加速度的表达式设做匀速圆周运动的物体的线速度的大小为v ，轨迹半径为r 。

（精心整理，诚意制作）5.6 向心加速度【学业达标测试】1.关于向心加速度的物理意义，下列说法正确的是（）A.它描述的是线速度方向变化的快慢B.它描述的是线速度大小变化的快慢C.它描述的是角速度变化的快慢D.它描述的是转速变化的快慢【解析】选A.匀速圆周运动的线速度大小和角速度都是不发生变化的，转速变化的快慢与角速度的变化快慢是对应的.所以B、C、D是错误的.向心加速度大小描述了物体线速度方向变化的快慢，向心加速度越大，v方向变化越快，A对.2.(20xx·中山高一检测)关于匀速圆周运动及向心加速度，下列说法中正确的是（）A.匀速圆周运动是一种匀速运动B.匀速圆周运动是一种匀速曲线运动C.向心加速度描述线速度大小变化的快慢D.匀速圆周运动是加速度方向不断改变的变速运动【解析】选D.匀速圆周运动的速度方向时刻改变，是一种变速曲线运动，A、B错.匀速圆周运动的加速度大小不变，方向时刻在改变，且加速度的大小描述了做匀速圆周运动的物体线速度方向变化的快慢，故C错、D对.L23.小金属球质量为m，用长L的轻悬线固定于O点，在O点的正下方处钉有一颗钉子P，把悬线沿水平方向拉直，如图5-6-3所示，若无初速度释放小球，当悬线碰到钉子后的瞬间（设线没有断）（）A.小球的角速度突然增大B.小球的线速度突然减小到零C.小球的向心加速度突然增大D.小球的线速度突然增大4.（20xx·温州高一检测）如图5-6-4所示为一皮带传动装置，右轮的半径为r，a为它边缘上一点，左侧是一轮轴，大轮的半径是4r，小轮的半径是2r.b点在小轮上，到小轮中心的距离为r，c点和d点分别位于小轮和大轮边缘上，若在传动过程中皮带不打滑.则（）A.a点与b点的线速度大小相等B.a点与b点的角速度大小相等C.a点与d点的线速度大小相等D.a点与d点的向心加速度大小相等5.如图5-6-5所示，长为l的细线一端固定在O点，另一端拴一质量为m的小球，让小球在水平面内做角速度为ω的匀速圆周运动，摆线与竖直方向成θ角，求小球运动的向心加速度.【解析】小球做匀速圆周运动的半径r=lsinθ向心加速度a=ω2r=ω2lsinθ.答案：ω2lsinθ一、选择题（本题包括5小题，每小题4分，共20分.至少一个选项正确）1.下列说法正确的是（ ）A.匀速圆周运动不是匀速运动而是匀变速运动B.圆周运动的加速度一定指向圆心C.向心加速度越大，物体速度的方向变化越快D.因为a= ，所以a与v2成正比2.（20xx·厦门高一检测）下列各种运动中，不属于匀变速运动的是（）A.斜抛运动B.匀速圆周运动C.平抛运动D.竖直上抛运动【解析】选B.匀变速运动指的是加速度不变的运动.据斜抛运动、平抛运动及竖直上抛运动的定义可知，三种运动中均是只有重力作用，运动的加速度都是重力加速度，即这三种运动都是匀变速运动，而匀速圆周运动的加速度方向指向圆心，故此加速度时刻在变化，匀速圆周运动属于变加速运动，符合题意的选项为B.3.一物体以4 m/s的线速度做匀速圆周运动,转动周期为2s,则物体在运动过程中的任一时刻,速度变化率的大小为（）【解析】选D.由于做变速运动的物体的速度变化率就是物体的加速度，本题中即为向心加速度，4.如图1所示,为A、B两质点做匀速圆周运动的向心加速度随半径变化的图象,其中A为双曲线的一个分支,由图可知（）A.A物体运动的线速度大小不变B.A物体运动的角速度大小不变C.B物体运动的角速度大小不变D.B物体运动的线速度大小不变5.（20xx·运城高一检测）如图2所示为两级皮带传动装置，转动时皮带均不打滑，中间两个轮子是固定在一起的，轮1的半径和轮2的半径相同，轮3的半径和轮4的半径相同，且为轮1和轮2半径的一半，则轮1边缘的a点和轮4边缘的c点相比（）A.线速度之比为1∶4B.角速度之比为4∶1C.向心加速度之比为8∶1D.向心加速度之比为1∶8二、非选择题（本题包括3小题，共30分.有必要的文字叙述）6.（思维拓展题）（9分）如图3所示，定滑轮的半径r=2cm，绕在滑轮上的细线悬挂着一个重物，由静止开始释放，测得重物以加速度a=2m/s2做匀加速运动，在重物由静止下落距离为1m的瞬间，求滑轮边缘上的点的角速度和向心加速度大小.7.（10分）如图4所示A、B、C分别是地球表面上北纬30°、南纬60°和赤道上的点.若已知地球半径为R，自转的角速度为ω0，求：（1）A、B两点的线速度大小.（2）A、B、C三点的向心加速度大小之比.［探究·创新］8.（11分）汽车以一定的速度在草原上沿直线匀速行驶，突然发现正前方有一壕沟，为了尽可能地避免掉进壕沟，通常有急转弯或急刹车两种方式.假设汽车急转弯做匀速圆周运动，急刹车做匀减速直线运动，且转弯时的向心加速度大小等于刹车时的加速度，请问司机是紧急刹车好，还是马上急转弯好？。

5.6 向心加速度课堂训练1．在一堂物理观摩课上，四名同学对于向心加速度提出了四种说法，请你帮助分析正误，肯定正确答案 （ ）A ．向心加速度的方向始终与速度的方向垂直B ．向心加速度的方向保持不变C ．在匀速圆周运动中，向心加速度是恒定的D ．在匀速圆周运动中，向心加速度的大小不断变化2．在匀速圆周运动中，下列物理量不变的是 （ ）A ．向心加速度B ．线速度C ．周期D ．角速度3．A 、B 两小球都在水平面上做匀速圆周运动，A 球的轨道半径是B 球轨道半径的2倍，A 的转速为30r/min ，B 的转速为15r/min 。

则两球的向心加速度之比为 （ ）A ．1：1B ．2：1C ．4：1D ．8：14．关于质点做匀速圆周运动的说法正确的是（ ）A ．由a=v 2/r 知a 与r 成反比B ．由a=ω2r 知a 与r 成正比C ．由ω=v/r 知ω与r 成反比D ．由ω=2丌n 知ω与转速n 成正比5．关于向心加速度的物理意义，下列说法正确的是 （ ）A ．它描述的是线速度方向变化的快慢B ．它描述的是线速度大小变化的快慢C ．它描述的是角速度变化的快慢D ．以上说法都不正确6．下列关于向心加速度的说法中正确的是 ( )A ．向心加速度的方向始终与速度方向垂直B ．在匀速圆周运动中，向心加速度是恒定的C ．做圆周运动时，向心加速度一定指向圆心D ．地球自转时，各点的向心加速度都指向地心7．如图6-18所示，O 1为皮带传动的主动轮的轴心，轮半径为r 1，O 2为从动轮的轴心，轮半径为r 2∶r 3为固定在从动轮上的小轮半径，已知r 2＝2r 1，r 3＝1.5r 1,A.B 和C 分别是3个轮边缘上的点，质点A.B.C 的向心加速度之比是 ( )A ．1∶2∶3B ．2∶4∶3C ．8∶4∶3D ．3∶6∶28．如图6-19所示，O 1和O 2是摩擦传动的两个轮子，O 1是主动轮，O 2是从动轮.若两轮不打滑，则对于两轮上a.b.c三点(半径比为1∶2∶1)，其向心加速度的比为A ．2∶2∶1B ．1∶2∶2C ．1∶1∶2D ．4∶2∶1图6-18 图6-19课外提升9、如图所示,A,B 两点做匀速圆周运动的向心加速度随半径变化的图象，其中A 为双曲线的一个分支,由图可知 ( ) A.A 物体运动的线速度大小不变B.A 物体运动的角速度大小不变C.B 物体运动的角速度大小不变D.B 物体运动的线速度大小不变10、图是物体由A 到D垂直，则下列说法中，正确的是： A 、D 点的速率比C 点速率大。

第五章曲线运动第六节向心加速度主备人：李超审核人：黄双平定稿时间：2012 年01月06日【学习目标】1、理解速度变化量和向心加速度的概念。

2、知道向心加速度和线速度，角速度的关系。

3、能够用向心加速度公式求有关问题。

【学习重点】理解匀速圆周运动中产生加速度的原因，掌握向心加速度的确定方法和计算公式。

【学习难点】向心加速度的方向的确定过程和其公式的推导过程。

【知识要点】一、速度变化量1、速度变化量是矢量，既有大小，又有方向。

2、速度变化量的运算法则：当初末速度不在一条直线上时，则△v的运算满足平行四边形法则二、向心加速度作匀速圆周运动的物体加速度指向圆心。

这个加速度称为向心加速度。

三、向心加速度的大小a n=v2/r , a n=rω2四、向心加速度的方向作匀速圆周运动的物体，一定有加速度，而速度大小要保持不变，故a n的方向一定垂直于速度方向，由于速度沿切线方向，故a n指向圆心。

【典型例题】【例题1】.关于北京和广州随地球自转的向心加速度，下列说法中正确的是（）A.它们的方向都沿半径指向地心B.它们的方向都在平行赤道的平面内指向地轴C.北京的向心加速度比广州的向心加速度大D.北京的向心加速度比广州的向心加速度小【答案】：BD◇听课记录【例题2】如图所示，为A、B两质点做匀速圆周运动的向心加速度随半径变化的图像．其中A为双曲线的一个分支、由图可知( )A．A物体运动的线速度大小不变B．A物体运动的角速度大小不变C．B物体运动的角速度大小不变D．B物体运动的线速度大小不变【答案】：AC◇听课记录【例题3】关于向心加速度的物理意义，下列说法中正确的是（）A.它描述的是线速度方向变化的快慢B.它描述的是线速度大小变化的快慢C.它描述的是角速度变化的快慢D.匀速圆周运动的向心加速度是恒定不变的【答案】A◇听课记录【例题4】做匀速圆周运动的物体，线速度为10m/s，物体从A到B速度变化量大小为10m/s，已知A、B间弧长是3.14m，则A、B弧长所对应的圆心角为多大？物体的向心加速度大小是多少？【答案】：速度是矢量，具有方向性，所以线速度与速度增量相同时，可以构成一个等边三角形，所以角度为60度。

六、向心加速度【要点导学】1、速度变化量Δv指末速度v2与初速度v1的差值，即Δv＝v2－v1。

注意，这里的差值并非速度大小相减的结果，而是两个速度矢量相减。

某一过程的速度变化量可按照以下方法求解：从同一点作出物体在一段时间的始末两个速度矢量v1和v2，从初速度v1的末端作一个矢量Δv至末速度v2的末端，所作矢量Δv就是速度的变化量。

2、做匀速圆周运动的物体，加速度方向始终指向，这个加速度叫做。

3、向心加速度的大小表达式有a n＝、a n＝等。

4、匀速圆周运动是一个加速度大小不变、方向时刻变化的变加速曲线运动。

【范例精析】例1一质点沿着半径r = 1 m的圆周以n = 1 r/s的转速匀速转动，如图，试求：(1)从A点开始计时，经过1/4 s的时间质点速度的变化；(2)质点的向心加速度的大小。

例2关于向心加速度，下列说法正确的是（）A．它是描述角速度变化快慢的物理量B．它是描述线速度大小变化快慢的物理量C．它是描述线速度方向变化快慢的物理量D．它是描述角速度方向变化快慢的物理量例3如图所示为质点P、Q做匀速圆周运动时向心加速度随半径变化的图线，表示质点P的图线是双曲线，表示质点Q的图线是过原点的一条直线。

由图可知（）A．质点P线速度大小不变B．质点P的角速度大小不变C．质点Q的角速度随半径变化D．质点Q的线速度大小不变【能力训练】1．由于地球的自转，地球表面上各点均做匀速圆周运动，所以（）A．地球表面各处具有相同大小的线速度B．地球表面各处具有相同大小的角速度C．地球表面各处具有相同大小的向心加速度D．地球表面各处的向心加速度方向都指向地球球心2．下列关于向心加速度的说法中，正确的是（）A．向心加速度的方向始终与速度的方向垂直B．向心加速度的方向保持不变C．在匀速圆周运动中，向心加速度是恒定的D．在匀速圆周运动中，向心加速度的大小不断变化3．由于地球自转，比较位于赤道上的物体1与位于北纬60°的物体2，则（）A．它们的角速度之比ω1∶ω2=2∶1B．它们的线速度之比v1∶v2=2∶1C．它们的向心加速度之比a1∶a2=2∶1D．它们的向心加速度之比a1∶a2=4∶14．关于质点做匀速圆周运动的下列说法正确的是（）A．由a=v2/r，知a与r成反比B．由a=ω2r，知a与r成正比C．由ω=v/r，知ω与r成反比D．由ω=2πn，知ω与转速n成正比5．A、B两小球都在水平面上做匀速圆周运动，A球的轨道半径是B球轨道半径的2倍，A的转速为30r/min，B的转速为15r/min。

上节课我们学了向心加速度，这节课我们来学习向心力。

我们在生活中其实经常遇到向心力和向心加速度，比如坐一些过山车之类的，大家会感觉整个身体快飞出去了。

其实那时候我们就在做圆周运动，在那种情况下我们应该很深刻的体会到向心力的可怕之处，感觉心脏都要跳出来了。

【视频】那这节课我们就一起来学习什么是向心力？向心力如何表达？以及向心力在生活中有着怎样的应用？好，首先我们看什么是向心力，即定义。

顾名思义，“向心力”F向就是：做圆周运动的物体，受到的指向圆心的力。

指向圆心简称“向心”。

那么这个力有什么特别之处吗？通过举一个例子大家来归纳。

这是一个圆周运动的轨迹，我们在其上标出4等分点A,B,C,D，我们知道曲线运动的速度沿着轨迹的切线方向，所以这4个点的方向是水平向右，竖直向下，水平向左，竖直向上的。

那下面我请4位同学结合定义（指向圆心的力）在黑板上标出这4个点受到的向心力的方向，注意把箭头画出来。

好，他们画完了。

同学们通过观察，发现这4个力都是指向圆心的，除此之外它们还有什么共同点吗？（标垂足）哎！它们是不是与速度都是垂直的？对，这就是向心力的第一个特征：方向始终与速度垂直，即θ=90°；那更深层次地，向心力还有没有其他特征呢？我们在本学期的第一节课就曾介绍过，当力与速度垂直时，只能改变速度的什么？方向不改变速度的大小。

而夹角小鱼90°，速度比变快；夹角大于90°，速度变慢。

所以向心力的第二个特征就是：只改变速度的方向，不影响速度的大小。

下一个问题是，向心力究竟从何而来？是你给它的还是从石头里蹦出来的？肯定有个出处。

所以我们要探究向心力的来源是什么。

好，这里举3个高考常见的模型。

第一个，我们在数学中用平行四边形表示平面，那这是一个平面，平面上有一个钉子，与钉子相连有一根绳子，绳子末端系一个小球，现在我们悠着小球在平面内做圆周运动，请问：小球受几个力？分别是什么？3个力，有重力（受力分析顺序：一种二弹三摩擦），支持力，还有什么？由于小球有一个向外飞的趋势，绳子就会绷紧，从而产生一个对小球的拉力。