自相关过程控制简介
- 格式:ppt
- 大小:770.00 KB
- 文档页数:38

自相关过程控制院系:管理科学与工程专业:质量与可靠性工程学号:110510335 姓名:张华威自相关过程质量控制引论:自相关过程质量控制概述当质量过程呈现自相关现象时,常规控制图已经不能准确反映生产中质量的波动.常规控制图理论:质量管理的观点认为:质量具有变异性其特性值是波动的,具有规律性,但它不是通常的确定性现象的确定性规律,而是随机现象的统计规律,用数学语言来讲,就是服从某种分布。
如果出现异常情况,就必然使波动偏离原来的分布,利用统计技术就可以发现这种波动。
在现代质量管理学中,通常使用休哈特控制图进行质量控制,但休哈特控制图的原理要求数据必须复合独立正态性,即要求数据服从正态分布,所以说如果数据之间彼此具有相关性的话,休哈特控制图便不再使用。
基于以上理论基础绘制的常规控制图虽然使用简便且易于理解,但对于受控状态下一般性原因的认知过于简化。
因此为了提高控制图对特殊性原因的检测能力,当过程相关时设计控制图,必须考虑质量过程的自相关结构。
为了解决过程自相关情况下的质量控制问题,统计学家们陆续提出了一些改进方法,其中主要方法之一就是引入时间序列分析法。
以ARMA以及ARIMA 模型为基础,我们便可以对具有相关性的一组数据进行相关性分析,方差分析,以及残差分析等,通过一系列控制图,便可以达到对具有自相关性的数据进行质量控制和质量改进的目的。
一、收集或生成反应自相关生产过程的平稳时间序列ARMA(p,q)数据:0.5377 0.1183 -0.6593 -1.8273 -0.93062.3339 0.5832 -1.9769 -1.5564 -1.2791-0.9306 -0.887 -1.0862 -1.3611 -0.59951.097 -1.3821 -1.6807 -1.9456 -0.37060.5881 -0.964 -0.8627 -0.3625 -1.2301-0.6845 0.636 -1.5359 -0.8981 -0.7563-0.5994 -0.7409 -0.5368 -1.2723 -0.912-0.1624 0.1918 0.0102 0.4458 -0.05523.3173 -0.352 1.556 -0.3836 0.79214.3794 0.9989 0.5869 -0.6471 1.48871.835 -0.6952 -1.3781 -0.7324 -0.9085.2662 -0.0154 -1.3526 -1.4082 -0.42463.909 0.3363 0.2649 -2.044 0.23763.4713 1.2641 -1.3455 1.0815 2.57693.6231 2.2772 0.3677 1.5831 0.69282.648 1.6038 -0.0958 1.4235 1.30682.2868 -0.0066 1.4991 -0.0704 0.77883.4275 -0.2645 -1.2401 -0.4736 -1.15163.8088 -1.1958 -0.368 -0.4345 -0.78114.3498 1.6732 -1.7639 0.4321 -2.53073.9891 -0.1377 1.9157 -1.2463 -0.3442.092 1.1812 1.2539 -2.8234 -0.59092.96 0.3569 2.5806 -3.2347 -2.14883.7378 1.4214 0.6083 -2.1308 -1.5373 3.2458 0.0529 0.6097 -1.6445 -2.2447 3.7789 -0.9494 0.2149 -1.0098 -2.5627 3.5901 -1.8812 1.3888 -1.1285 -3.1112 2.6253 -0.7372 0.481 -0.6835 -2.858 2.6835 -1.1103 1.3587 -1.1565 -4.3651.3421 -0.9724 -1.2282 0.0787 -2.07562.3645 0.6 -0.5603 -1.6693 0.3241 0.4378 0.2999 -1.4722 -0.356 0.1171 -0.1406 0.5277 -2.4813 -1.5275 -0.1473 -0.7485 1.9415 -1.1743 -1.2054 -0.0155 -3.3607 0.3246 -1.0496 -0.5082 -0.0006 -0.4665 1.4414 -0.8436 0.4234 0.8211 -0.9163 1.6532 -2.0703 -1.0584 1.9373 -1.353 1.0153 -0.1608 0.8585 1.6819 0.4189 1.2193 -0.3513 0.7719 1.2125 -1.908 -0.2516 -0.5229 0.5756 1.736二、建立过程的时间序列模型建模步骤:a :传统修哈特控制图分析:首先对所生成数据作正态性检验概率图P值大于0.05,服从正态分布作均值极差控制图控制图X 的Xbar 控制图检验结果检验1。



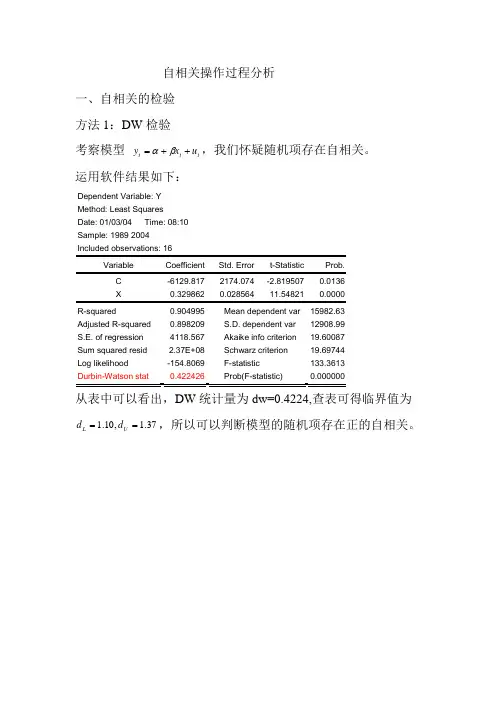
自相关操作过程分析一、自相关的检验 方法1:DW 检验考察模型 t t t u x y ++=βα,我们怀疑随机项存在自相关。
运用软件结果如下:Dependent Variable: Y Method: Least Squares Date: 01/03/04 Time: 08:10 Sample: 1989 2004 Included observations: 16C -6129.817 2174.074 -2.819507 0.0136 X0.3298620.02856411.548210.0000 R-squared0.904995 Mean dependent var 15982.63 Adjusted R-squared 0.898209 S.D. dependent var 12908.99 S.E. of regression 4118.567 Akaike info criterion 19.60087 Sum squared resid 2.37E+08 Schwarz criterion 19.69744 Log likelihood -154.8069 F-statistic 133.3613 Durbin-Watson stat0.422426 Prob(F-statistic)0.000000从表中可以看出,DW 统计量为dw=0.4224,查表可得临界值为37.1,10.1==U L d d ,所以可以判断模型的随机项存在正的自相关。
方法2:直接检验法(回归检验法) 一阶自相关形式为:t t t v u u +=-1ρ即对模型t t tv e e +=-1ρ进行回归,进行T 检验,判断系数是否为0.结果如下:在EVIEW 软件中常用)(k X -表示变量的X 的滞后k 阶变量。
Dependent Variable: E Method: Least Squares Date: 01/03/04 Time: 08:19 Sample(adjusted): 1990 2004R-squared0.565485 Mean dependent var -167.2139 Adjusted R-squared 0.565485 S.D. dependent var 4059.960 S.E. of regression 2676.235 Akaike info criterion 18.68655 Sum squared resid 1.00E+08 Schwarz criterion 18.73375 Log likelihood-139.1491 Durbin-Watson stat0.750574可写出模型为19818.0ˆ-=t t e e ,因为1-t e 的系数的T 检验的犯错概率为0.0008,远远地小于0.05,这说明系数显著地不为0。




第6章自相关1. 自相关定义1)非自相关由第2节知回归模型的假定条件之一是,Cov(u i,u j )=E(u i u j) =0, (i, j∈T, i ≠ j),(1.1)即误差项u t的取值在时间上是相互无关的。
称误差项u t非自相关。
2)自相关如果Cov (u i ,u j ) ≠ 0, (i ≠ j)则称误差项u t存在自相关。
自相关又称序列相关。
原指一随机变量在时间上与其滞后项之间的相关。
这里主要是指回归模型中随机误差项u t 与其滞后项的相关关系。
自相关也是相关关系的一种。
2.自相关类型1)自相关按滞后阶数可分为两类。
(1)一阶自回归形式当误差项u t只与其滞后一期值有关时,即u t = f (u t - 1),称u t具有一阶自回归形式。
(2) 高阶自回归形式当误差项u t的本期值不仅与其前一期值有关,而且与其前若干期的值都有关系时,即u t = f (u t – 1, u t – 2 , … ), 则称u t 具有高阶自回归形式。
2)按函数形式分为线性自相关和非线性自相关 (1)线性自相关 f 为线性函数形式 (2)非线性自相关 f 为非线性函数形式 3.一阶线性自相关通常假定误差项的自相关是线性的。
因计量经济模型中自相关的最常见形式是一阶自回归形式,所以下面重点讨论误差项的线性一阶自回归形式,即 u t =1a u t -1 + v t (1.2)其中1a 是自回归系数,v t 是随机误差项。
v t 满足通常假设E(v t ) = 0, t = 1, 2 …, T, Var(v t ) = σv 2, t = 1, 2 …, T,Cov(v i , v j ) = 0, i ≠ j, i, j = 1, 2 …, T, Cov(u t-1, v t ) = 0, t = 1, 2 …, T,依据普通最小二乘法公式,模型(1.2)中 1 的估计公式是,1ˆa= ∑∑=-=-Tt t Tt t tuuu 22121 (1ˆβ=∑∑---2)())((x x x x y y t t t ) (1.3)其中T 是样本容量。

自相关过程的控制图研究摘要:常规控制图的一个基本假设前提是:从过程获得的观测值彼此时间是相互独立的,然而在现实中存在大量具有自相关性的过程,违背独立性建设。
所以使用常规控制图对平稳的自相关过程进行控制时,会出现大量的虚假报警,从而导致错误的判断,控制图的效用会大为降低。
本文通过对自相关过程中常规控制图进行分析,指出其问题,并运用支持向量机制作残差控制图进行自相关过程控制。
关键词:自相关过程控制;控制图;支持向量机Abstract: The conventional control chart is a basic assumption: the observations obtained from the process each time is independent of each other, but in reality there is a lot of the process of self-correlation, against the independence of the building. Therefore, use of conventional control chart on the smooth control of the autocorrelation process, there will be a large number of false alarms, leading to incorrect judgments, the effectiveness of control charts will be greatly reduced. Based on the autocorrelation of conventional control chart the course of the analysis points out the problems and make use of support vector machines residual control chart for autocorrelated process control.Key words: self-related process control; control chart; support vector machine自相关过程的控制图研究 (1)1.引言 (3)1.1选题的意义 (3)1.2 本文的内容 (3)2.自相关过程常规控制图的局限性 (4)2.1 控制图基础理论 (4)2.1.1 统计过程控制 (4)2.1.2 控制图定义 (5)2.1.3 两种错误 (6)2.1.4 一种简单常规控制图——单值控制图 (7)2.3 自相关过程概述 (8)2.4 常规控制图运用于自相关过程的局限性 (8)3.自相关过程的控制图研究 (10)3.1残差控制图 (10)3.2支持向量机运用于残差控制图 (12)3.2.1 最小二乘支持向量机 (12)3.2.2 用最小二乘支持向量机制作残差控制图 (13) (14)3.3实验研究 (14)3.3.1 受控状态下的控制图研究3.3.2 失控状态下的控制图研究 (20)3.4 检测效率分析 (27)3.4.1平均链长 (27)3.4.2控制图效率比较分析 (27)3.5 结果分析 (27)4.案例分析 (28)4.1 案例说明 (28)4.2 运用残差控制图分析 (28)5总结 (30)1.引言1.1选题的意义要想在市场上立于不败之地,就要满足越来越严格的质量要求,生产出世界级质量的产品。

自相关通俗理解
一、什么是自相关
自相关(Autocorrelation),又称为自相关函数,是描述一个时间序列在不同时间滞后之间的相关性的统计量,它主要用于分析连续数据点之间的关系,以便弄清数据的结构、关系,以及建立数据模型,常用于统计分析中。
二、自相关的用例
自相关用于分析数据在不同时间点之间的相关性,常用于预测经济走势、电力系统的震荡、疾病模型预测,用于测验样本的随机性以及多元回归分析中的多重共线性检验等。
三、自相关的计算
自相关是由特定的自相关函数(ACF)和偏自相关函数(PACF)来计算的,自相关函数用于表示任意时刻与某一时刻之前的滞后时间的相关性,偏自相关函数用于表示任意时刻与某一时刻之前的滞后时间之间的非线性相关性。
四、自相关的应用
1. 用于预测:自相关技术可以用来预测未来趋势、潜在的变化点。
通过分析不同时间点之间的自相关性,可以推断出未来发展的方向,给出未来的预测结果,为企业决策提供参考依据。
2. 用于模型建立:自相关技术可以用来研究不同时间点之间的联系,分析数据的结构和关系,建立有效的模型,以确保模型能够更好地拟合和预测数据。
3. 用于风险控制:自相关技术可以用来识别时间序列可能存在的超出正态分布以外的特殊变异,从而可以避免风险,提高企业的财务效益。
第六章 自相关一、什么是自相关及其来源 二、自相关的后果三、自相关的检验 四、自相关的修正五、应用实例6.1自相关的概念及其来源例如:研究中国工业总产值指数(Y )和国有企业工业总产值指数(X )的关系,利用1977年至1997年的历史资料,运用OLS 方法得到如下模型。
2ˆ0.0568 1.0628(37.8666)(0.3502)(0.0015)(3.0348)0.32650.37679.2099t t Y X t R DW F =+====给定显著性水平a=0.05,自由度为19,查t 分布表得0.025(19) 2.093t =。
以模型的计算结果t=3.0348,且0.025(19)t t >,表明t X 对t Y 的影响比较显著,但可决系数并不理想。
这种情况下,随机扰动项之间有可能存在序列自相关。
一、自相关的概念自相关(auto correlation )又称序列相关(serial correlation ),是指总体回归模型的随机误差项i u 之间存在的相关关系。
更一般的,自相关是指某一随机变量在时间上与其滞后项之间的相关。
经典回归模型中,曾假定随机误差项无自相关,即i u 在不同观测点之间是不相关的。
(,)(,)0()i j i j Cov u u E u u i j ==≠如果该假设不成立,就称i u 与j u 存在自相关,即不同观测点上的误差项彼此相关。
二、自相关产生的原因 1)经济系统的惯性。
自相关现象大多出现在时间序列数据中,其本期值往往受滞后值影响,突出特征就是惯性和低灵敏度。
例如:居民总消费函数模型01(1,2,,)t t tC Y u t n ββ=++=总消费受收入(t Y )的影响,事实上消费也受消费习惯的影响。
把消费习惯并列随机扰动项中,就可能出现序列相关性。
2)经济行为的滞后性例如,基础设施的建设需要一定的建设周期,那么产出效益的发挥有一定滞后时间。
第五讲、自相关1、自相关的概念:古典线性回归中假设扰动项u i中不存在自相关,即E(u i u j)=0, i≠j这表明任一观察值的扰动项不受其他观察值的扰动项的影响。
但是如果存在E(u i u j) ≠0, i≠j表明存在自相关问题。
自相关通常与时间序列数据有关,但截面数据中也可能产生自相关的问题(空间相关),例如,某一家庭消费支出的增加可能影响不愿比别人逊色的另一家庭消费支出的影响。
图a-d表明扰动项u存在可辨别的模式(可能存在自相关),而图e则表明不存在系统模式(可能不存在自相关)。
2、导致自相关的因素:(1)在涉及时间序列数据的回归方程中,大多数经济时间序列数据的一个显著特征是“惯性”或“延迟性”。
如GDP、就业、货币供给等时间序列都呈现周期性,连续的观察值之间很可能存在相互依赖或是相关的。
(2)模型设定错误:应该包括在模型中的重要变量未包括进模型(过低设定)或模型选择了错误的函数形式,这时残差会呈现出系统模式。
(3)蛛网现象:即解释变量是时间滞后变量,即具有时间滞后效应。
如农产品供给模型中价格对供给的影响存在蛛网现象(滞后效应)。
这种情况下的扰动项不是随机的。
(4)数据加工:在实证研究中,通常原数据是要经过加工的。
例如季度数据的时间序列回归中,数据通常是由月度数据按季相加再平均得到,而这种“平滑”过程的本身可能导致扰动项的系统模式,从而产生自相关。
3、自相关的后果:(1)虽然最小二乘估计仍然是线性和无偏的,但不是有效的,即最小二乘估计量(OLS)不是最优线性无偏估计量(BLUE)。
(2)OLS估计量的方差是有偏的,计算OLS估计量的方差或标准差的公式可能严重低估真实的方差或标准差,从而导致常用的t检验和F检验是不可靠的。
(3)通常计算的R2也是不可靠的。
4、自相关的诊断自相关的诊断存在异方差诊断中的类似问题,即ui是无法观察的,而且也不知道其产生机制:我们通过OLS估计,仅仅得到的是ei,通过对ei的讨论来“了解”自相关是否存在。
解读如下:GB/T 17989《控制图》计划分为以下9个部分:第1部分:通用指南;第2部分:常规控制图;第3部分:验收控制图;第4部分:累积和控制图;第5部分:特殊控制图;第6部分:指数加权移动平均控制图;第7部分:多元控制图;第8部分:短周期和小批量控制方法;第9部分:自相关过程控制图。
本文对GB/T 17989的第2部分:常规控制图进行解读。
该标准给出了理解和应用常规控制图进行统计过程控制的指南适用于使用常规控制图进行统计过程控制的情形,所有涉及的补充内容均与常规控制图相关,诸如:警戒限的使用、趋势模式和过程能力分析等。
该标准将代替GB/T 4091 -2001《常规控制图》该标准指出,对于一个受控的过程,超出控制限(平均值±3西格玛)是很偶然的小概率事件。
故而,当一个点落在控制限外时,需要采取行动。
3西格玛控制限通常作为行动限。
同时,在控制图上,对中心线两侧的2西格玛处进行标注是有价值的。
任何落在2西格玛界限之外的点都将作为出现失控状态的警告。
因此2西格玛限称为警戒限。
超警戒限的点并不需要采取措施。
但是可以立即采集另一个样本以确定是否要有相应的纠正措施。
该标准给出了选择不同类型控制图的决策树:与GB/T 4091-2001相比,增加了4种异常波动的检验模式;给出了这四种检验模式所提示的警戒:检验1:表示存在失控状态检验2:表示过程均值或波动性已经偏离中心线检验3:表示过程出现有规则的线性趋势检验4:表示过程出现非随机或周期性模式当然,这些检验模式虽然提高了过程失控的检测能力,但也提高了虚发报警的概率,只使用检验1虚发报警率为3‰,同时应用检验1~3的虚发报警概率约为10‰。
检验模式的选择应基于过程的通常状态来确定,而不是套用模板给出了西部电器的八大判异规则,可作为补充增加了计量控制图的构建方法:给出了通过过程控制、过程能力分析进行过程改进的策略初始数据的采集,推荐25组,要求过程不应受到原材料、操作者、操作方法、机器的设置等外部因素带来的间歇性影响。
stm32自相关算法摘要:1.STM32 自相关算法概述2.STM32 自相关算法的原理3.STM32 自相关算法的实现4.STM32 自相关算法的应用5.总结正文:【1.STM32 自相关算法概述】STM32 自相关算法是一种基于STM32 微控制器的算法,用于处理信号处理、图像处理等领域中的自相关问题。
这种算法通过在STM32 上运行程序,实现对输入数据的自相关处理,以达到提取特征、降维等目的。
【2.STM32 自相关算法的原理】STM32 自相关算法的核心思想是利用自相关函数来处理输入数据。
自相关函数是一种统计学方法,用于衡量数据之间的相关性。
在信号处理和图像处理中,自相关函数可以用来提取特征、降维等。
STM32 自相关算法通过在STM32 上运行程序,实现对输入数据的自相关处理,从而实现数据特征的提取和降维。
【3.STM32 自相关算法的实现】STM32 自相关算法的实现主要包括以下几个步骤:(1)数据预处理:对输入数据进行预处理,包括数据规模化、数据归一化等。
(2)自相关函数计算:利用自相关函数计算输入数据的自相关值。
(3)自相关特征提取:根据自相关值的大小,提取输入数据的自相关特征。
(4)数据降维:根据自相关特征,对输入数据进行降维处理。
以上步骤通过在STM32 上运行程序来实现,从而完成对输入数据的自相关处理。
【4.STM32 自相关算法的应用】STM32 自相关算法广泛应用于信号处理、图像处理等领域。
例如,在图像处理中,STM32 自相关算法可以用来提取图像的特征,用于图像识别、目标检测等任务。
在信号处理中,STM32 自相关算法可以用来提取信号的特征,用于信号识别、信号分析等任务。
【5.总结】STM32 自相关算法是一种基于STM32 微控制器的算法,用于处理信号处理、图像处理等领域中的自相关问题。
这种算法通过在STM32 上运行程序,实现对输入数据的自相关处理,以达到提取特征、降维等目的。