描点画对数函数的图象

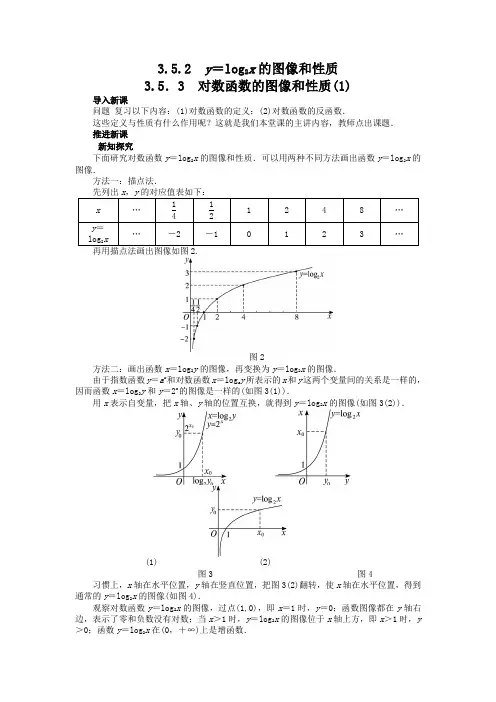
3.5.2 y＝log2x的图像和性质3.5．3 对数函数的图像和性质(1)导入新课问题复习以下内容：(1)对数函数的定义；(2)对数函数的反函数．这些定义与性质有什么作用呢？这就是我们本堂课的主讲内容，教师点出课题．推进新课新知探究下面研究对数函数y＝log2x的图像和性质．可以用两种不同方法画出函数y＝log2x的图像．方法一：描点法．图2方法二：画出函数x＝log2y的图像，再变换为y＝log2x的图像．由于指数函数y＝a x和对数函数x＝log a y所表示的x和y这两个变量间的关系是一样的，因而函数x＝log2y和y＝2x的图像是一样的(如图3(1))．用x表示自变量，把x轴、y轴的位置互换，就得到y＝log2x的图像(如图3(2))．(1) (2)图3 图4 习惯上，x轴在水平位置，y轴在竖直位置，把图3(2)翻转，使x轴在水平位置，得到通常的y＝log2x的图像(如图4)．观察对数函数y＝log2x的图像，过点(1,0)，即x＝1时，y＝0；函数图像都在y轴右边，表示了零和负数没有对数；当x＞1时，y＝log2x的图像位于x轴上方，即x＞1时，y ＞0；函数y＝log2x在(0，＋∞)上是增函数．对数函数y＝log a x(a＞0，a≠1)，在其底数a＞1及0＜a＜1这两种情况下的图像和性定义域：(0，＋∞)定义域：(0，＋∞)值域：R值域：R(1,0)，即x＝1时，(1,0)，即x＝1时，＞1时，y＞0；＞1时，y＜0；＜1时，y＞0提出问题根据你掌握的知识目前比较数的大小有什么方法？判断函数的单调性有哪些方法和步骤？判断函数的奇偶性有哪些方法和步骤？活动：学生回忆，教师引导，教师提问，学生回答，学生之间可以相互交流讨论，学生有困难教师点拨．问题(1)学生回顾数的大小的比较的方法，有些数一眼就能看出大小，有些数比较抽象，就用到某些函数的图像和性质，要分别对待，具体问题具体分析．问题(2)学生回顾判断函数的单调性的方法和步骤，严格按步骤与规定．问题(3)学生回顾判断函数的奇偶性的方法和步骤，严格按步骤与规定．讨论结果：(1)比较数的大小：①作差，看两个数差的符号，若为正，则前面的数大．②作商，但必须是同号数，看商与1的大小，再决定两个数的大小．③计算出每个数的值，再比较大小．④是两个以上的数，有时采用中间量比较．⑤利用图像法．⑥利用函数的单调性．(2)常用的方法有定义法、图像法、复合函数的单调性的判断．利用定义证明单调性的步骤：①在给定的区间上任取两个自变量的值x1，x2，且x1＜x2.②作差或作商(同号数)，注意变形．③判断差的符号，商与1的大小．④确定增减性．对于复合函数y＝f[g(x)]可以总结为：当函数f(x)和g(x)的单调性相同时，复合函数y＝f[g(x)]是增函数；当函数f(x)和g(x)的单调性相异即不同时，复合函数y＝f[g(x)]是减函数．又简称为口诀“同增异减”．(3)有两种方法：定义法和图像法．利用定义判断函数奇偶性的格式步骤：①首先确定函数的定义域，并判断其定义域是否关于原点对称；②确定f(－x)与f(x)的关系；③作出相应结论：若f(－x)＝f(x)或f(－x)－f(x)＝0，则f(x)是偶函数；若f(－x)＝－f(x)或f(－x)＋f(x)＝0，则f(x)是奇函数．图像法：偶函数的图像关于y轴对称；奇函数的图像关于原点对称．这也可以作为判断函数奇偶性的依据．下面看它们的应用．应用示例例1 比较下列各组数中的两个值的大小：(1)log 25.3，log 24.7；(2)log 0.27，log 0.29；(3)log 3π，log π3；(4)log a 3.1，log a 5.2(a ＞0，a ≠1)．活动：学生思考、交流，教师要求学生展示自己的思维过程，并及时评价．对(1)与(2)由数形结合的方法或利用函数的单调性来完成，直接利用对数函数的单调性；作出图像，利用图像法比较；计算出结果；作差利用对数函数的性质．对(4)因为底数的大小不确定，因此要分别讨论，再利用对数函数的单调性；作差利用对数函数的性质；转化为指数函数，再由指数函数的单调性判断大小．对(3)两个对数式的底数和真数均不相同．设法找到一个具体的对数函数，根据这个函数的单调性来比较它们的大小，题中所给的对数式的底数和真数都不相同，可以找一个中间量作为桥梁，通过比较中间量与这两个对数式的大小来比较对数式的大小，一般选择“0”或“1”作为中间量进行比较．解：(1)解法一：用图形计算器或多媒体画出对数函数y ＝log 2x 的图像，如图5.图5在图像上，横坐标为4.7的点在横坐标为5.3的点的下方，所以log 24.7＜log 25.3.解法二：由函数y ＝log 2x 在R ＋上是单调增函数，且4.7＜5.3，所以log 24.7＜log 25.3.(2)因为0.2＜1，函数y ＝log 0.2x 是减函数，7＜9，所以log 0.27＞log 0.29.(3)解法一：因为函数y ＝log 3x 和函数y ＝log πx 都是定义域上的增函数，所以log π3＜log ππ＝1＝log 33＜log 3π.所以log π3＜log 3π.解法二：直接利用对数的性质，log π3＜1，而log 3π＞1，因此log π3＜log 3π.(4)解法一：当a ＞1时，y ＝log a x 在(0，＋∞)上是增函数，且3.1＜5.2，所以log a 3.1＜log a 5.2.当0＜a ＜1时，y ＝log a x 在(0，＋∞)上是减函数，且3.1＜5.2，所以log a 3.1＞log a 5.2. 点评：对数函数的单调性取决于对数的底数是大于1还是小于1.而已知条件并未指明时，需要对底数a 进行讨论，体现了分类讨论的思想，要求学生逐步掌握．同时本题采用了多种解法，从中还体现了数形结合的思想方法，要注意体会和运用.变式训练比较log 20.7与log 130.8两值的大小．解：考查函数y ＝log 2x .因为2＞1，所以函数y ＝log 2x 在(0，＋∞)上是增函数．又0.7＜1，所以log 20.7＜log 21＝0.再考查函数y ＝log 13x ，因为0＜13＜1，所以函数y ＝log 13x 在(0，＋∞)上是减函数． 又1＞0.8，所以log 130.8＞log 131＝0.所以log 20.7＜0＜log 130.8.点评：题中所给的对数式的底数和真数都不相同，可以找一个中间量作为桥梁，通过比较中间量与这两个对数式的大小来比较对数式的大小，一般选择“0”或“1”作为中间量进行比较，这里的中间量是0.例2 求下列函数的定义域：(1)y＝log a x2；(2)y＝log a(4－x)．活动：学生回忆，教师提示，学生展示解题过程，教师巡导，及时评价学生．此题主要利用对数及对数函数的定义及y＝log a x的定义域(0，＋∞)求解．教师引导，学生回答，求函数定义域时应首先考虑函数解析式，这两类题既有二次根式，又有对数和指数式，且真数和指数中含有变量，因此考虑被开方数非负；零和负数没有对数等；转化为不等式来解．解：(1)要使函数有意义，则需x2＞0，即x≠0，所以定义域为{x|x≠0}；(2)因为4－x＞0，即x＜4，所以函数定义域为{x|x＜4}．点评：该题主要考查对数函数及其性质，根据函数的解析式，列出相应不等式或不等式组，解不等式或不等式组即可．课堂小结本节课复习了对数函数及其性质，借助对数函数的性质的运用，我们对函数的单调性和奇偶性又进行了复习巩固，利用单调性和奇偶性解决了一些问题，对常考的内容进行了学习，要高度重视，特别是要和高考接轨，注意题目的形式和难度．课后作业 p97 A组3补充：1．求函数y＝lg x＋lg(5－2x)的定义域．(x2－2x－3)的单调区间，并用单调定义给予证明．2．求函数y＝log123．已知y＝log a(2－a x)在[0,1]上是x的减函数，求a的取值范围．。

课件3 描点画对数函数的图象课件编号：ABⅠ-2-2-1.课件名称：描点画对数函数的图象.课件运行环境：几何画板4.0以上版本.课件主要功能：配合教科书“2.2.2 对数函数及其性质”的教学，说明对数函数图象的画法，演示对数函数图象的性质．课件制作过程（一）：（1）新建画板窗口．单击【Graph】（图表）菜单中的【Define Coordinate System】（建立直角坐标系），建立直角坐标系．选中原点，按Ctrl＋K，给原点加注标签A，并用【文本】工具把标签改为O．（2）单击【Graph】菜单的【New Parameter】（新建参数），弹出“New Parameter”对话框，如图1，把Name栏改为x，把Volum栏改为0.5，单击【OK】后，出现参数x＝0.5．再新建参数y＝－1，n＝0（用来控制迭代次数）．图1 图2（3）单击【Measure】（度量）菜单中的【Calculate】（计算）打开计算器，计算“x×2”以及“y＋1”的值，如图2．（4）先后选中x，y，单击【Graph】菜单的【Plot As （x，y）】（绘制点（x ，y ）），画点（x ，y ）．（5）单击【Display 】菜单的【Trace Plotted Point 】（追踪点的轨迹）．（6）先后选中x ，y ，n ，按住Shift 键，单击【Transform 】（变换）菜单的【Iterate To Depth 】（带参数的迭代），如图3，弹出“Iterate ”对话框，依次单击“x 2”，“y ＋1”，最后单击【Iterate 】完成迭代，如图4．图3 图4（7）先后选中x ，y ，x ×2以及y ＋1，单击【Display 】菜单的【Hide Measurements 】（隐藏目标）．（8）单击【Graph 】菜单的【Plot Points 】（绘制点）画点E （－0.5，0）．再画点F （8，0）．（9）选中两点E ，F ，按Ctrl ＋L 键画线段EF ．单击【Construct 】菜单的【Piont On Segment 】（在线段EF 上构造点A ）．（10）单击【Measure 】（度量）菜单中的【Abscissa （x ）】（度量点的横坐标），打开计算器，计算log A x 2的值，如图5．图5（11）先后选中x，log2xA，单击【Graph】菜单的【Plot As （x，y）】（绘制点（x，y））画点B．再先后选中点B，A．单击【Construct】菜单中的【Locus】构造点B的轨迹．并利用【Construct】菜单中的【Piont On Locus】构造轨迹上的点M，如图6．把点M置于（0.5，－1）处，然后隐藏x，log2x A，B，A及所作的轨迹．图6（12）选中点M，单击【Display】菜单的【Trace Objects】（追踪点的轨迹）．（13）选中点M，单击【Edit】菜单，在【Action Buttons】菜单中的【Animation】菜单作动画按钮．（14）单击【Graph】菜单的【Plot New Function】（绘制新函数），新建x的图象．函数f（x）＝log2图7（15）选中f（x）的图象，单击【Edit】菜单的【Action Buttons】中的x图象的按钮【Show Function Plot】．【Hide/Show】，设置隐藏函数f（x）＝log2课件制作过程（二）：log x的图象，只要按前面所述的“函数f 要用描点法求作函数f（x）＝12（x）＝log2x图象的作法即可”．也可以利用简易的方法来作它的图象，具体操作如下：（1）新建画板窗口（或直接在该窗口上继续作图）．（2）单击【Graph】菜单的【New Parameter】（新建参数），弹出“New Parameter”对话框，输入x＝0.5，单击确定即可．（3）单击【Measure】（度量）菜单中的计算，弹出新建计算对话框，输入log x，单击确定即可．12（4）在空白处单击释放一切选择对象，依次选取x＝0.5，y＝－1，单击【Graph】菜单的绘制点，同时弹出直角坐标系．（5）在空白处单击释放一切选择对象，选择文本工具，给原点标签，并改为O．（6）在空白处单击释放一切选择对象，依次选取x＝0.5，y＝－1，单击【Graph】菜单的【Tabulate】（制表），坐标系中出现表格．（7）选中x＝0.5，y＝－1及表格，按住Shift键，再按＋键，每按一下，表格新增一行，点也多描一个．课件使用说明：1．在几何画板 4.0以上版本环境下，打开课件“描点画对数函数的图象.gsp”．2．“描点画对数函数的图象.gsp”由4页组成．第1页是使用说明；第2、3、4页分别表现用描点法画对数函数的图象的过程，这些函数分别是log2x；12log x．3．第2页的使用说明．选中计算列表下面的迭代参数n=1和反映函数值的表格，并同时按Shift 键及＋键，每按一下，表格多增一行，坐标平面就多一个点，如图8．图8再用鼠标单击动画按钮【Animate Point】，出现描点过程，最后按【Show Function Plot】键，显示函数f（x）= log2x图象，如图9 ．图9这样就完成了计算、列表、描点、连线的整个绘图过程．4．第3页的使用与第二同．log x的对称性而5．第4页为说明两个函数f（x）＝log2x与g（x）＝12设置的，只要依次单击这两个按钮就可以了．。