正交设计助手实例

正交试验设计经典案例
一、L9(3^4)正交试验设计
这个实验设计是一个L9(3^4)正交试验设计，用于研究铜锌合金中锌的含量、冶炼时间、冷却速率和成型压力对铜锌合金硬度的影响。

在这个设计中，有四个因素（锌的含量、冶炼时间、冷却速率和成型压力）和三个水平（低、中、高）。

该试验的九个试验条件如下表所示。

2、L16(4^5)正交试验设计
这个实验设计是一个L16(4^5)正交试验设计，用于研究发酵生产中，发酵液pH 值、生物量、发酵温度、曲菌培养基和曲菌翻转次数对干酪根的质量影响。

在这个设计中，有五个因素（发酵液pH值、生物量、发酵温度、曲菌培养基和曲菌翻转次数）和四个水平（低、中低、中高、高）。

该试验的十六个试验条件如下表所示。

3、L16(4^5)正交试验设计
这个实验设计是一个L16(4^5)正交试验设计，用于研究太阳能集热器的建造，包括集热面积、集热器长度、集热器宽度、太阳能采集器的形状和位置对太阳能集热器效率的影响。

在这个设计中，有五个因素（集热面积、集热器长度、集热器宽度、太阳能采集器的形状和位置）和四个水平（低、中低、中高、高）。

该试验的十六个试验条件如下表所示。

以上这些都是经典的正交试验设计案例，这些设计都遵循着统计学中的一些原则和方法，有效地结合了多个因素的影响，将因素控制在一定范围内，从而帮助我们更好地理解问题并提出相应的解决方案。

正交设计举例正交设计是一种研究多因素多水平的设计方法，它根据正交性从全面试验中挑选出部分有代表性的点进行试验。

这些代表性的点具备了“均匀分散，齐整可比”的特点，是一种高效率、快速、经济的实验设计方法。

以下是正交设计的一个具体例子：假设某建筑材料研究院想要研究如何提高粉煤灰砖的抗折强度。

在这个试验中，有三个因素可能会影响抗折强度，分别是成型用水量、碾压时间和每次碾压的料重。

每个因素都有三个水平，例如成型用水量可以是9%、10%、11%，碾压时间可以是8min、10min、12min，每次碾压的料重可以是330kg、360kg、400kg。

如果进行全面试验，需要进行3^3=27种组合的实验，且尚未考虑每一组合的重复数。

但是，如果采用正交设计，可以选择一个三因素三水平的正交表，例如L9(3^4)，只需要进行9次试验。

这9次试验将涵盖所有因素的所有水平，而且每个因素的每个水平都会与其他因素的每个水平组合一次，且仅组合一次。

具体的试验方案可以如下安排：试验1：成型用水量9%、碾压时间8min、每次碾压的料重330kg试验2：成型用水量9%、碾压时间10min、每次碾压的料重360kg试验3：成型用水量9%、碾压时间12min、每次碾压的料重400kg试验4：成型用水量10%、碾压时间8min、每次碾压的料重360kg试验5：成型用水量10%、碾压时间10min、每次碾压的料重400kg试验6：成型用水量10%、碾压时间12min、每次碾压的料重330kg试验7：成型用水量11%、碾压时间8min、每次碾压的料重400kg试验8：成型用水量11%、碾压时间10min、每次碾压的料重330kg试验9：成型用水量11%、碾压时间12min、每次碾压的料重360kg通过这9次试验，可以找出影响抗折强度的最优组合。

这种方法大大减少了试验次数，提高了效率，而且能够得到全面试验的效果。

正交设计20220425180006一、正交设计简介正交设计是一款专注于实验设计与数据分析的智能工具，旨在帮助研究人员、工程师及各类实验爱好者快速、高效地进行正交实验设计。

通过本，用户可以轻松完成实验因素的筛选、实验水平设置、正交表以及实验结果分析，从而提高实验的准确性和效率。

二、功能特点1. 智能推荐正交表：根据用户输入的实验因素和水平，自动推荐合适的正交表，确保实验设计的科学性和合理性。

2. 一键实验方案：用户只需简单设置实验因素和水平，系统便会自动实验方案，节省实验设计时间。

3. 数据分析与图表展示：实验结束后，用户可导入实验数据，系统将自动进行数据分析，并以图表形式展示，便于用户直观了解实验结果。

4. 智能优化实验方案：根据实验结果，系统可提供实验方案的优化建议，助力用户进一步提高实验效果。

5. 云端存储与共享：支持实验数据云端存储，方便用户随时随地查看、分享和协作。

三、操作指南1. 注册登录：访问正交设计官网，注册账号并登录。

2. 创建实验项目：“创建实验”，填写实验名称、实验目的等信息。

3. 设置实验因素和水平：在“实验因素”模块，添加实验因素并设置相应水平。

4. 正交表：“推荐正交表”，系统将根据实验因素和水平智能推荐正交表。

5. 实验方案：确认正交表无误后，“实验方案”，并打印实验方案。

6. 实施实验：按照实验方案进行实验操作，记录实验数据。

7. 数据分析与优化：实验结束后，导入实验数据，系统将自动进行分析并展示图表。

根据分析结果，系统将提供实验方案优化建议。

四、应用场景1. 产品研发：帮助研发人员优化产品配方、工艺参数，提高研发效率。

2. 质量控制：用于分析影响产品质量的因素，制定合理的质量控制措施。

3. 教育培训：辅助教师和学生进行实验设计，提高实验教学效果。

4. 科研实验：为科研人员提供高效的实验设计工具，助力科研成果产出。

五、用户反馈与支持1. 在线客服：用户在使用过程中遇到任何问题，可通过官网在线客服功能寻求帮助。

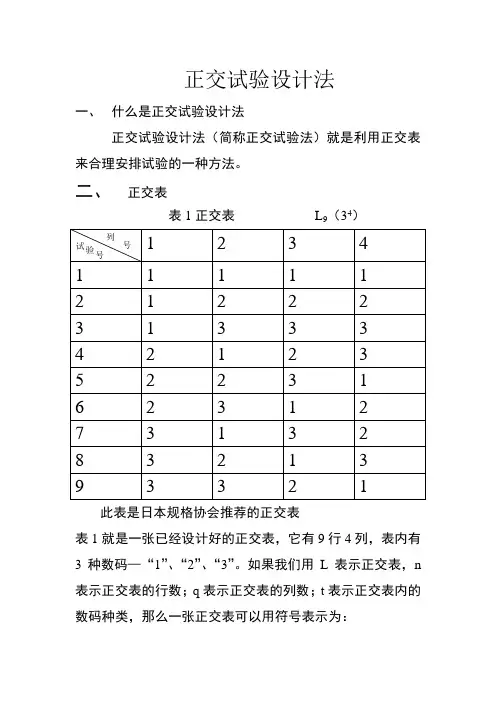
正交试验设计法一、什么是正交试验设计法正交试验设计法（简称正交试验法）就是利用正交表来合理安排试验的一种方法。

二、正交表表1正交表L9（34）此表是日本规格协会推荐的正交表表1就是一张已经设计好的正交表，它有9行4列，表内有3种数码—“1”、“2”、“3”。

如果我们用L表示正交表，n 表示正交表的行数；q表示正交表的列数；t表示正交表内的数码种类，那么一张正交表可以用符号表示为：例如：L9（34）正交表，最多可以安排4个因素做试验，每个因素可取3个水平，共有9种试验方案，这显然大大减少了试验方案是数量，因为如果安排4因素3水平的全搭配试验必须有34=81次试验方案才行。

三、正交表的优点多：可以考虑多因素，多指标。

快：试验周期短，见效快。

好；可以找到最佳方案。

省：试验次数少。

假如：考虑十三个因素，三水平的试验。

用L27（313）安排只要做27次试验。

而进行全面试验时，则要做313=1594323次试验，如果每天做10次试验，也要做436.8年之久方可做完.四、正交试验表的种类分两类：一类是水平数相同的正交表，即正交表中每一列所包含的代表水平的数码是一样的。

例如：L4（23）、L8（27）、L9（34）等等。

另一类是水平数不同的正交表，例如：L8（41×24）、L18（21×37）、L18（61×36）、L16（42×212）L32（49×24）。

L8（41×24）L16（42×212）四：常用正交试验设计与分析步骤1、明确试验目的2、确定考察指标3、挑因素选水平4、设计试验方案5、实施试验方案6、试验结论分析7、验证试验8、结论与建议例：设计纸飞机试验1、试验目的：找到一组飞行距离最远的纸飞机设计参数。

2、考察指标Y——纸飞机飞行距离。

3、挑因素选水平分析：影响Y的重要因素A：材料B：尺寸C：抛出力D：抛出角度根据实际情况每个因素取3个水平制定因素水平表因素水平表4、设计试验方案由因素水平表可以清楚的看出，这是一项4因素3水平的试验，必须有3种数码的正交表中找到合适的表安排此项试验，这类表试验次数最少的是L9（34）表于是就选L9（34）正交表安排试验方案。

《实验设计》课实验报告
姓名：张冬冬学号：913116120239
实验二
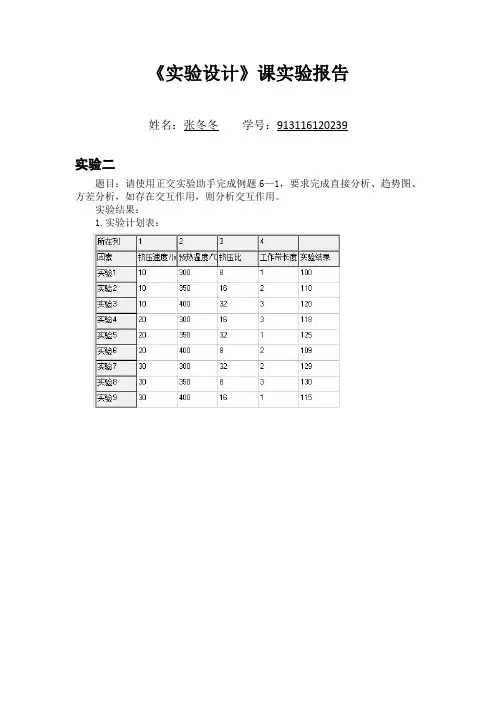
题目：请使用正交实验助手完成例题6—1，要求完成直接分析、趋势图、方差分析，如存在交互作用，则分析交互作用。

实验结果：
1.实验计划表：
从上图来看，第8号实验的直线长度最长，但第7号方案为129mm，非常接近。

因此第8号实验方案不一定就是最优方案，需要进一步分析寻找可能的更好方案。

3.效应曲线图：
由图可得挤压速度、挤压比、工作带长度越高越好，预热温度取中间值可得理论上的最佳工艺。

由上图得：挤压速度>挤压比>工作带长度>预热温度。

材料工艺实验的极差与方差分析一、实验目的1．学习掌握正交试验设计方法，安排多因素、多水平试验;2．学会用极差法、方差分析和交互作用对实验结果进行分析，确定最佳工艺条件(最优水平组合)；3．提高运用计算机解决实际问题的能力。

二、实验原理我们把在试验中考察的有关影响试验指标的条件称为因素（也叫因子），把在试验中准备考察的各种因索的不同状态(或配方)称为水平。

在研究比较复杂的工程问题中，往往都包含着多个因素，而且每个因素要取多个水平。

对于包含五个因素、五个水平的工程项目，理论计算必须进行55＝3125次试验。

显然，所需要的试验次数太多了，工作量太大。

实践告诉我们，合理安排试验和科学分析试验，是试验工作成败的关键。

试验方案设计的好，试验次数就少，周期也短，这样不仅节省了大量人力、物力、财力和时间，而且可以得到理想的结果。

相反，如果试验设计安排的不好，即使进行了很多次试验，浪费了大量材料、人力和时间，也不一定能够得到预期的结果。

正交试验法，就是在多因素优化试验中，利用数理统计学与正交性原理，从大量的试验点中挑选有代表性和典型性的试验点，应用“正交表”科学合理地安排试验，从而用尽量少的试验得到最优的试验结果的一种试验设计方法。

正交试验法也叫正交试验设计法，它是用“正交表”来安排和分析多因素问题试验的一种数理统计方法。

这种方法的优点是试验次数少，效果好，方法筒单，使用方便，效率高。

由于试验次数大大减少，使得试验数据处理非常重要。

我们可以从所有的试验数据中找到最优的一个数据，当然，这个数据肯定不是最佳匹配数据，但是肯定是最接近最佳的了。

用正交表安排的试验具有均衡分散和整齐可比的特点。

均衡分散，是指用正交表挑选出来的各因素和各水平组合在全部水平组合中的分布是均衡的。

整齐可比是说每一因素的各水平间具有可比性。

最简单的正交表L4(23)如表-1所示。

表-1记号L4(23)的含意如下：“L”代表正交表；L下角的数字“4”表示有4横行(简称为行)，即要做四次试验；括号内的指数“3”表示有3纵列(简称为列)，即最多允许安排的因素个数是3个；括号内的数“2”表示表的主要部分只有2种数字，即因素有两种水平l与2，称之为l 水平与2水平。