工程物理基础 第1篇 声学基础 第2章 弹性体的振动
- 格式:pptx
- 大小:606.04 KB
- 文档页数:57

本《声学基础》考试⼤纲适⽤于中国科学院研究⽣院声学等专业的硕⼠研究⽣⼊学考试。
声学是物理学的⼀个分⽀,主要研究与声有关的各种现象,包括⼈⽿不能听到的超声波和次声,声学基础是与声学各个分⽀学科的基础,是与声相关的研究和应⽤的基础课程。
要求考⽣掌握声学基相关的机械振动的基本概念与基本运算,并具有⼀定的灵活应⽤的能⼒。
⼀、考试内容
(⼀)简单振⼦的振动
1.简单振⼦的概念,运动⽅程和规律;
2.⾃由振动、衰减振动和受迫振动的概念;
3.共振频率的计算;
4.振动能量及转化的概念和计算。
(⼆)弹性体的振动
1.⽆限长弦的振动⽅程和解;
2.两端固定的弦的共振频率;
3.模式的概念;
4.棒的横振动、膜和板的振动概念。
(三)声波的基本性质
1.线形声波⽅程的基本假设和推导;
2.平⾯波的基本性质,声压级和声强级的概念;
3.平⾯声波在平⾯界⾯上反射和折射的研究⽅法,⼀般规律;
(四)管道和房间中的声波
1.声波导中模式的概念,频散现象;
2.房间中声场的模式;
3.混响时间的概念和计算;
(五)声波的辐射
1.球⾯波的基本性质;
2.辐射阻抗的概念;
3.偶极源的辐射。
⼆、主要参考书⽬
声学基础(第2版),杜功焕、朱哲民、龚秀芬著,南京⼤学出版社(2001年)。



第一部分:声学基础篇*******************第一章:声学基础********************第1节:物理声学基础一、声音的本质1、声波的产生及传播声音产生于物体的振动,声音是在弹性介质中传播的频率在20至20000Hz的机械纵波。
低于20Hz的声波叫次声波,高于20000Hz的声波称为超声波。
次声波、超声波人耳都听不见,但它与声波的本质相同。
由此可见,要产生声音必须有振动和传播正动的弹性介质,而要听到声音除存在声源,要有传播媒介外,还必须通过人耳听觉感知。
才能产生声音的感觉.◆图片1-1声波的产生和传播过程中学课本将声波的传播用投石入水现象和甩绳实验作了形象的比喻。
◆图片1-2 投石入水现象◆图片1-3 甩绳实验横波的特点是质点的振动方向与波的传播方向相互垂直。
纵波又称疏密波是质点的振动方向与传播方向一致的波。
振动和波动是相互联系的运动形式,但是两个不同的概念,振动是波动产生的根源,波动是振动的传播过程。
声音的本质是一种波动,是声能在随声波在传播。
一般把声能的物理传播过程称为声波,而把声能的人耳感知过程叫做声音。
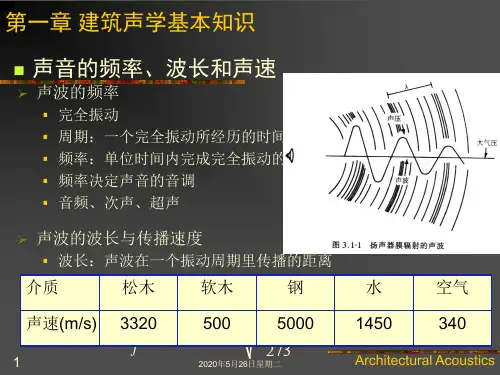
2、声波的表征(周期、频率、波长、波度,声场的基本概念及自由声场的传播)周期是指声源完成一次振动所经历的时间,记作T,单位为秒(s).一秒钟内振动的次数称为频率,记作f,单位为赫兹(Hz),它是周期的倒数,即f=1/T.声波传播速度是指声波在媒质中每秒传播的距离,简称声速.记作c单位为米/秒(m/s).声速不是质点振动的速度而是振动状态的传播速度,它的大小与振动的特性无关,而与媒质的弹性,密度和温度有关.声波的传播速度实质是媒质分子向相邻分子作动量传递的快慢程度.显然,媒质分子结构越紧密,内损耗特性越小,声速值就越大.例如,空气,水,钢铁的媒质特性决定了它们的声速值约为1:4:12.声波的波长是指声源完成一周的振动,声波所传播的距离,或者说声波在传播途径上相位相同的两相邻质点之间的距离,记作λ,单位为米(m). 因此,声速.波长和频率三者有如下的关系:c=λf或c=λ/T由于一定媒质的声速为常数,故频率与波长呈反比关系.例如室温空气中频率f=100赫兹的波长为3.4m,f=1000赫兹的波长为0.34m或34cm声场指的是媒体中有声波存在的时空区域,声波在各向同性无反射均匀媒体中产生的声场称为自由声场。



弹性力学中的弹性体的振动和谐振频率弹性体是指在外力作用下,能够发生形变,但在外力作用消失后,又能够恢复原状的材料。
在弹性体的振动过程中,涉及到振动和谐共振频率的概念。
本文将探讨弹性力学中的弹性体的振动和谐共振频率,并介绍相关理论和应用。
一、弹性力学基础在深入理解弹性体的振动和谐共振频率前,先了解一些弹性力学的基础知识是必要的。
弹性力学是研究物体在外力作用下产生形变的一门学科。
在弹性力学中,有两个重要的基本方程:胡克定律和牛顿第二定律。
胡克定律是描述物体弹性形变的关系,简单来说就是弹性体的形变与受力成正比。
具体公式为:F = -kx其中,F表示受力,k表示弹簧系数,x表示形变。
牛顿第二定律是描述物体受力与加速度之间关系的定律。
其公式为:F = ma其中,F表示受力,m表示物体质量,a表示加速度。
二、弹性体的振动当一个弹性体受到外力作用后,如果形变足够小,就可以认为弹性体是弹性的,可以发生振动。
弹性体的振动有两种基本形式:自由振动和受迫振动。
1. 自由振动自由振动是指弹性体在没有外力作用下的振动。
当弹性体受到外力作用后,会发生形变,但是外力消失后,弹性体会按照自己的固有特性恢复原状,继续向前振动。
弹性体的自由振动是周期性的,振动的周期取决于弹性体的固有特性,与外力无关。
2. 受迫振动受迫振动是指弹性体在外力作用下的振动。
外力可以是周期性的,弹性体会跟随外力的周期进行振动,这种振动称为强制振动;外力也可以是非周期性的,弹性体会根据外力的不同而产生各种不规则的振动。
三、弹性体的谐振频率在自由振动中,弹性体的振动可以通过谐振频率进行描述。
谐振频率是指使得振动呈现最大幅度的频率。
在弹性体受到自由振动的情况下,当振动频率等于谐振频率时,振幅最大;当振动频率与谐振频率有一定偏差时,振幅逐渐减小。
弹性体的谐振频率与弹性体的固有特性有关。
根据弹性力学的理论,谐振频率与弹性体的质量和弹性系数相关。
谐振频率可用以下公式表示:f = 1 / (2π) * √(k / m)其中,f表示振动的频率,k表示弹簧系数,m表示物体质量。

物理声学与振动知识点物理声学和振动是物理学的重要分支,研究声音的产生、传播和接收,以及振动的本质和规律。
在本文中,我们将介绍一些物理声学和振动的基本知识点。
一、声音和声波声音是由物体振动引起的机械波。
当物体振动时,它会使周围的空气分子也跟着振动,从而产生声波。
声波是一种机械波,需要介质(如空气、水等)传播。
声音的特性主要包括以下几个方面:1. 频率:声音的频率决定了其音调,单位是赫兹(Hz)。
2. 音量:声音的音量决定了其大小,单位是分贝(dB)。
3. 声速:声音在某种介质中的传播速度,单位是米/秒(m/s)。
声波传播的过程可以用波动方程来描述,该方程是一维波动方程,可以用来解释声音在空气中的传播。
此外,声音还受到反射、折射、衍射和干涉等现象的影响。
二、波的特性和传播1. 波的类型:波可以分为机械波和电磁波两种类型。
声波属于机械波,电磁波包括光波和无线电波等。
2. 直线传播:波可以在一定介质中直线传播,以直线传播的波称为平面波。
3. 弯曲传播:波在传播过程中会发生弯曲,这种现象称为折射。
折射现象是由于介质的密度不均匀引起的。
4. 反射和干涉:波在遇到障碍物时会发生反射,反射后的波将从不同的方向传播。
当两个或多个波相遇时,它们会发生干涉现象。
5. 衍射:波在遇到障碍物或缝隙时,会发生辐射和弯曲,这种现象称为衍射。
三、频率和音调频率是声音的一个重要特征,它决定了声音的音调。
频率越高,音调越高;频率越低,音调越低。
人耳能够感知的声音频率范围大约在20 Hz到20 kHz之间。
四、共振和谐振声音的共振现象是指当物体受到外界震动的作用力与其固有频率相同时,物体会发生共振现象,振动幅度会增大。
共振现象在日常生活中很常见,如鸟在振动的树枝上唱歌。
五、声音的衰减和吸收声音在传播过程中会因为各种原因而逐渐衰减,比如空气阻力、声波的散射和吸收等。
声音的衰减是指声音强度逐渐减弱,直到消失。
六、声音的测量和应用声音可以通过声压级和声强来进行测量。

大学物理声学与振动声学与振动是大学物理学中的一个重要领域,探讨了声波和振动的基本原理、特性和应用。
本文将介绍声学与振动的基础知识,包括声波的传播、声音的特性、振动的基本概念以及其在实际应用中的作用。
一、声波的传播声波是一种机械波,需要介质来传播。
当物体振动时,会产生压缩和稀疏的区域,从而形成了声波。
声波在空气、液体和固体等介质中的传播速度不同,一般在空气中的传播速度约为343米/秒。
声波的传播需要满足一定条件,包括介质的弹性和惰性。
弹性使得介质可以恢复到原来的形状,而惰性使得介质的分子能够传递能量。
声波的传播过程中,能量从振动源传递到周围的领域,形成了声压波和相应的声音。
二、声音的特性声音是由声波引起的感知现象。
人耳对声音的感知主要包括声音的强度、频率和音调。
声音的强度与声波的振幅有关,振幅越大,声音的强度越大。
声音的强度单位是分贝(dB),正常人耳可以听到大约0-120dB的声音。
声音的频率是指单位时间内声波振动的次数,单位是赫兹(Hz)。
人耳可听到的频率范围约为20Hz到20000Hz。
不同频率的声音会产生不同的音高,高频率的声音听起来较高,低频率的声音听起来较低。
音调是对音高感知的主观评价,通常分为高音、中音和低音。
音乐中使用不同的音调来表达情感和意义。
三、振动的基本概念振动是物理系统围绕平衡位置做周期性的往复运动。
振动可以分为机械振动和非机械振动。
机械振动是指由物体的弹性力恢复驱动的振动,如弹簧振子和摆钟的摆动等。
非机械振动是指由电磁力、重力等非弹性力引起的振动,如声波和电磁波等。
振动的特性可以用频率、周期、振幅和相位等来描述。
频率是指单位时间内振动的次数,周期是振动完成一次往复运动所需的时间。
振幅是振动运动的最大偏离距离,相位是振动物体的位置相对于某一时刻的偏移量。
四、声学与振动的应用声学与振动的理论与实践在许多领域都有广泛的应用。
在音乐产业中,声学和振动学的理论被用来研究和改进音乐乐器的设计和制造。