相量图图解法在正弦交流电路解题中的应用策略

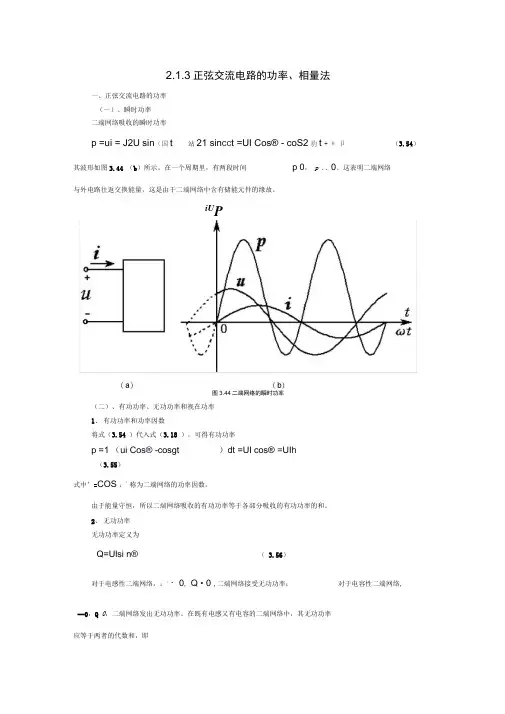
2.1.3正弦交流电路的功率、相量法一、正弦交流电路的功率（一）、瞬时功率二端网络吸收的瞬时功率p =ui = J2U sin（国t 站21 sin cc t =UI Cos® - coS2豹t + ® 卩（3.54）其波形如图3.44 （b）所示。

在一个周期里，有两段时间p 0，p .. 0。

这表明二端网络与外电路往返交换能量，这是由于二端网络中含有储能元件的缘故。

iU P图3.44二端网络的瞬时功率（二）、有功功率、无功功率和视在功率1、有功功率和功率因数将式（3.54 ）代入式（3.18 ），可得有功功率p =1 （ui Cos® -cosgt ）dt =UI cos® =UI h（3.55）式中’=COS ：：称为二端网络的功率因数。

由于能量守恒，所以二端网络吸收的有功功率等于各部分吸收的有功功率的和。

2、无功功率无功功率定义为Q=Ulsi n® （3.56）对于电感性二端网络，：：・0, Q • 0 ,二端网络接受无功功率；对于电容性二端网络,--0，Q 0，二端网络发出无功功率。

在既有电感又有电容的二端网络中，其无功功率应等于两者的代数和，即图3.45功率三角形S p ；p 2 Q 2 tan■ = cos=p(3.58)(3.59)(3.60)正好构成一个直角三角形（如图 3.45所示），称为功率三角形。

例3.25试求图3.46所示电路的有功功率、无功功率和视在功率，其中 尺=2OJR 2 =1OJC =2mF,L =0.1H ,u =50 2sin100tV 。

22Mt图 3.46 例 3.25解:Q = Q L Q C一般来说，二端网络吸收的无功功率等于各部分吸收的无功功率的代数和。

3、视在功率 视在功率定义为S =UI（ 3.57）其SI 主单位为伏安（VA ），工程上也常用千伏安（KVA ）。

由于电机和变压器的容 量是由它们的额定电压和额定电流来决定的，因此可以用视在功率来表示它们的容量。

182.5 j132.5 225.536
③旋转因子 复数
特殊旋转因子
jF
Im
F
ej =cos
+jsin =1∠
Im F• ej
π , 2
π j π π e 2 cos jsin j 2 2
F• ej
旋转因子 0
0
Re
jF


F Re

o 例1 已知 i 141.4sin(314t 30 )A u 311.1sin(314t 60o )V 试用相量表示i, u .
i(t ) 2I sin( t Ψ ) I I Ψ
相量的模表示正弦量的有效值;

解
I 10030o A,


U 220 60o V
正弦量为周期函数
周期T 和频率f
t
f(t)=f ( t+k )
f
1 T
6. 三相电路的计算
周期T ：重复变化一次所需的时间。单位：秒s 频率f ：每秒重复变化的次数。 单位：赫(兹)Hz
正弦电路
激励和响应均为同频率的正弦量的线性电路 （正弦稳态电路）称为正弦电路或交流电路。
研究正弦电路的意义
i (t ) I m sin( t Ψ ) 2 I sin( t Ψ )
同理，可得正弦电压有效值与最大值的关系：
U
1 Um 2
或
U m 2U
若交流电压有效值为 U=220V ，
U=380V
②测量中，交流测量仪表指示的电压、电流读 数一般为有效值。 ③区分电压、电流的瞬时值、最大值、有效值的 符号。
结论
对正弦电路的分析研究具有重要的理论价 值和实际意义。

浅析正弦交流电路的相量法解题作者：陈新芬来源：《速读·上旬》2015年第12期教学中笔者发现，在高职学生电路分析的教材中，关于正弦交流电的相量法分析，大多数的教科书都是直接给出具体的解题步骤，但对其中隐含的一部分电路特性的说明、描述线性电路的数学方程的特点、相量法来源的简单介绍有所欠缺，导致学生对此方法的掌握和熟练应用都存在一定的困难。

本文就关于正弦交流电路的相量法进行简单程度的来龙去脉的分析讲解，旨在让高职的学生能够在阅读此文后，对电路分析中的相量法有一个更加深刻的理解和掌握，便于熟练应用于各种电路模型的分析计算。

正弦交流电是人类智慧的创造发明，现实生活中，大型电站发电、传输、供电以及耗电基本都是发生在正弦稳态的条件下;其次，掌握正弦电路的行为是分析非正弦电路的前提，再次，正弦稳态可以简化电力系统的设计，在很多场合下，设计师首先设计出吻合正弦交流电要求的电力设备，而后，此设备对于非正弦交流电通常也会有令人满意的响应结果。

在研究电路对正弦交流电的响应时，首先明确电路的研究范围，我们这里的电路是线性电路，所以有必要对线性电路的概念进行简单讲述。

一、线性电路线性电路是指完全由线性时不变无源元件、独立源或线性受控源构成的电路。

线性就是指输入和输出之间关系可以用线性函数表示，从而使之与非线性区分开来。

线性电路最基本的特性应该是它具有叠加性与均匀性。

叠加性与均匀性的含义可以用图1来说明。

<D：＼书＼排版＼速读·上旬201512＼速读排版12上定稿打包＼Image＼image1.png>图1：线性电路示意图图1电路中，x表示加在电路上的输入信号，即激励;y表示电路对该输入信号产生的输出，即响应。

叠加性的含义：若激励x1产生的响应为y1，激励x2产生的响应为y2，则当x1和x2共同作用于电路时产生的响应为y1+y2。

均匀性的含义：若激励x作用于电路产生的响应为y，则激励kx作用于电路产生的响应必为ky。

相量图绘制
通过将相量按照比例放置在复平面内，可以直观地表 示出各相量之间的关系。
相量图分析
通过观察相量图，可以分析出电路的阻抗、功率和相 位差等参数。
相量法的应用场景
01
正弦稳态电路分析
相量法主要用于分析正弦稳态电 路，包括交流电路和含有正弦激 励的动态电路。
02
交流电路参数计算
03
控制系统分析
利用相量法可以方便地计算交流 电路的阻抗、功率和相位差等参 数。
03
对于多输入多输出系统，相量法可能无法 给出完整的描述。
04
相量法不能处理瞬态响应或非正弦激励的 问题。
未来研究方向与展望
01
研究方向
02
深入研究相量法的数学基础和物理意义，提高其理论水平。
探索相量法与其他电路分析方法的结合，如频域分析、时域分
03
析等。
未来研究方向与展望
• 研究如何将相量法应用于非线性系统和时变系统。
实例三：RLC电路的正弦稳态响应分析
总结词
RLC电路的正弦稳态响应具有谐振特性，其频率由L、C和R的比值决定。
详细描述
RLC电路的正弦稳态响应表现为一个具有谐振峰的波形，其频率由电感L、电容C和电阻R的比值决定，即谐振频 率f=1/2π√(LC/R^2)。在RLC电路中，当频率f等于谐振频率时，电路的阻抗最小，电流最大；当频率f远离谐振 频率时，电路的阻抗增大，电流减小。
相量法简介
定义
01
相量法是一种将正弦稳态的时域问题转化为复数02
通过相量法，可以更方便地分析交流电路的响应，包括电压、
电流和阻抗等。
优势
03
相量法简化了计算过程，使得复杂问题变得简单直观。

U
U
2 R
U C2

82 112 13.60V
电压表读数为 13.60V ．
此题的相量图也可按比例画出，用尺子量 U 得
的长度即为电压表读数．
（b）此电路图为ＲＬ并联电路，设电压 U U0V，
考虑到 IR 和 U 同相，IL 滞后 U 90 且由ＫＣＬ得
I IR IL
4-37(a)所示． 解: (a)设： I I0A ．根据Ｒ、Ｌ、Ｃ各元件的电
压电流的相量关系以及电路的ＫＶＬ方程
U U R U L UC
可定性画出相量图如图4－36，当 U LU时C 为图
4－36（a）所示，这时 ，0即 U 超前 的相位为 的电路为感性电路；当 U LU C 时 I 0 ，为电阻性电路如图4－36（b）所示；
IR仍与U同相， I仍为
IR 、IL 、IC的和，即正确
体现电路的基本定律是画 相量图的基本要求．
例4-15 电路相量模型如图4-39所示。已知 I1 10A ，
，I 2 20A ，U 220V ，R2 5 ，I 与U 同相。
求：I R X 2 及XC 。
分析：由题中给出的条件 I 与U 同相，设 U 2200 为参考相量画相量图。
画出相量图如图4－35(b)所示．由直角三角形
ＯＡＢ可得
IL
I2

I
2 R

52 32 4A
电流表读数为４Ａ．
此题也可按比例用几何方法画出相量图，然后用量尺
测出 IL 的长度值即为电流表读数．
例 4-14 定性画出ＲＬＣ串联电路和ＲＬＣ并联电路的 相量图，它们的电路相量图模型如图4-36(a)和图
根据题意可知 I UR 与 U 同相，且UC U UR 由相量图

设 1C= R 将电源看作是 Y 联接, 由于负载为 不对称 Y 联接, 故使用中点电压法分析计算。 设 UA= UP 0 V, 则 U B= 2UPV, U C= UPV
图7
负载的中点电压:
UN N=
j
1 R
UP
+
2U P
1 R
+
UP
j
1 R
+
1 R
+
1 R
1 R
=
j+ 2+ j+ 2
UP=
- 1+ j+ 2
收稿日期: 2003- 09- 12 作者简介: 高艳平( 1970- ) 女, 河南荥阳人, 郑州铁路职业技术学院电气工程系讲师。
陈 林( 1964- ) 女, 湖北武汉人, 郑州铁路职业技术学院电气工程系助理讲师。
29
= 111. 72
U2= 7 180- 111. 72= 7 68. 28V 或 7 - 68. 28
Z=
R+
j 1C=
R-
j
1 C
| Z| = R2+ ( 1C) 2 1) R 增大, | Z| 增大, Ucd一定, I 减小, Ubd减小。 R 增大至无限大时, | Z| , I 减小至零, Ubd 减小至零, b 点和 d 点近于重合。 2) R= 0 时, b 点和 c 点同电位, U bd= U cd, b 点 和 c 点重合。 所以随着 R 由大到小地改变, 输出电压 U ab 的 有效值不变, 等于输入电压的一半。 Uab和 U cd的相 位差则在 0 ~ 180 的范 围内变 化。
第 17 卷 第 1 期 2005 年 3 月
郑州铁路职业技术学院学报 Journal of Zhengzhou Railway Vocational College

２ ０ ￣０ ８ ０ ７ ２ ０
学年 等衄
表 １２ 方法 ２ （）
！ 乜ｒ挂
蕊 插
求 姐蝌
ｔ ｉ ７
靛
４ ５
电路分 析等 蕈 ，都可统 ‘ 剑栩 模型 电路中来 ，都 统 ‘ 公式 Ｕ＝／ 】 到 ＝ ｚ中 求，
ｊ 不过 问的 电路 结构 ，复ｍ抗ｚ ｛ 的袈 达式 不同 存 教学巾 ， 对教材 的这 ｒ 个斑 的内容 作 ＿ Ｆ ！ 『 如 处理 ： 在 ‘ 参数 元 电路
交流 电路 。如嘲 １ ．复阻抗 』 中 ， 一 拖之 Ｉ ，弼采 用巍流 串联 电路 的分 ． 目ｆ 联
救警 嚣 疗 ℃ 连艇
析方 法 ，计算电路 的总ｍ抗 ｚ＝Ｒ＋ｊ 一 ） （ ，这 些都是 学生所 熟悉 的知 识， Ｘ
易于接 受 ，思维 疗式不 变。ｆ ｆ： ａｂ ｉ 意运 算过程要遵 德相。： 聚 或复数 的运算法 ７２ ｝、
学年 分始 术 拖 ≈
｝ ＋ Ｃ： ＃ｌ
－
］－ ＿
最模 电路
图 】
啦 ｒ投
砖船 ０ １ ６６ 蕞 ４ ５
（） ａ 交流 电路
进 捋 器材 ｛ 丹数段 鲫诂以ｊ ，
窀 ｉ 龋 借、弼：靛 岛萼蟊爵嗽版牲 薮 ７ 舒比 ， ％ ５６
一
相 量模 型 教 学效 果
３ 涉及 知识 ．
教 材 内容 及 教 学 方 法 上 的 调 整 在以前 的中职教学中 ， 交流 电路的教 学遵循 教材 的编排顺 序 ， 学生 学
、
用相量模 型来分析计算交流电路 ， 要求学生具有 一定 的复数及复数 运
习感到困难 ， 常忽略或弄错了相位关系 ； 经 在引入相量模 型后 ， 对教材 的内 算知识 ， 如复数 的四则运算 、 复数的表示方法及相 互转换 ， 复数的模及 幅角 容及教学方法上要作相应调 整或 处理 ， 循循序 渐进 的原则 ， 之符合 学 的计 算等 ， 遵 使 这些知识在前一学期 中的课程 内容 已学过 ， 在教材 中也有体 现 ，

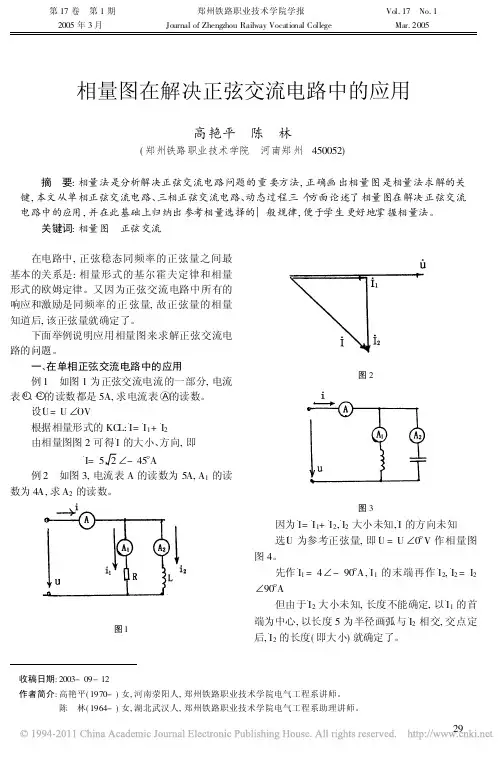
利用相量图分析正弦稳态电路(南京邮电大学)摘要：相量图在分析正弦稳态电路中具有重要的地位。

文中介绍了相量图在分析正弦稳态电路中的几种作用。

关键字：正弦稳态电路，相量，相量图引言在正弦稳态电路中，激励和响应通常用三角函数和波形图来表示，因而在分析交流电路时常常会涉及到不同频率的三角函数间的加减等运算。

由于运算十分复杂，所以我们常把正弦稳态电路中的正弦量用相量形式表示，这样便把复杂的三角运算化成了复数运算，避免了微分方程的建立。

在许多情况下，如果能将相量法结合相量图分析，可以简洁、直观地表达电路的性质，同时更进一步地简化运算，为计算提供解题思路。

1. 相量图1.1定义由于每一个复数都在复平面中对应一个矢量，我们将这种在复平面中表示相量的图称为相量图。

在完成正弦量的相量表示后，在相量图中，原先正弦量的加（减）运算结果便成了在复平面中对应矢量根据平行四边形定则相加（减）得到的和矢量。

由此，我们可以看出利用相量图表示正弦量本质上属于数学变换。

因此利用相量图分析正弦稳态电路具有合理性，并不会改变电路的性质。

1.2相量图法基本方法以电路中各元件上相同的物理量作为参考相量（幅角为零），利用KVL ，KCL 的相量表达形式和三种基本元件（电阻、电感、电容）的VCR 关系用相量图表示出来，根据各有向线段的几何关系求解相应物理量的方法叫做相量图分析法。

2. 相量图在正弦稳态电路分析中的应用2.1简单串并联电路中在简单串并联电路中，相量图的作用主要是简化相量运算，将相量加减运算转化为几何上的矢量加减。

画相量图时，首先选择参考相量,即人为设一相量，其幅角为0°。

+1图12.1.1 简单串联电路在分析简单串联电路时，通常选择电流为参考相量。

例：如图2，求图中电压表示数。

分析：R 上的R U 和I同相，L 上L U比I 朝前90°，C 上CU 比I落后90°。

则可取电流I 为参考相量，并规定其幅角为0°，根据基尔霍夫电压定律的相量形式，U =R U +LU +C U . 在相量图中可以如图3表示，由图可知：同样根据相量图，我们可知由端口看去电路呈现感性，电压幅角为：2.1.2简单并联电路在分析简单并联电路时，元件共享电压变量，所以我们通常选择电压为参考相量。

图5 图 10
复平面上有向线段 叠加可 用三角 形法 则或平 行四 边
形法则, 即可得图 11
图6 3. 3 纯电容元件
电路如图 7 所示, 已 知 C 元件 元件 特性方 程的 相量 表达式为 ÛU= ÛI ( - jXC ) , 根据复阻抗 的定义, ZC = - jXC = X Cej ( - 90b) , 根 据复 阻抗的 物理 意义, Qu - Qi = - 90b, 即电 容元件上电压比电流滞后 90b相量图如图 8 所示。
定律的熟练运 用, 对 三种 基本 元件 的相 位 关系 的熟 练 掌 握, 对复阻抗物理意义的深刻理解。
[ 参考文献]
[ 1] 秦 曾 煌. 电 工 学: 上 册 [ M ] . 北 京: 高 等 教 育出 版 社,
1999. [ 2] 邱关源. 电路[ M ] . 北京: 高等教育出版社, 1999.
理意义, 具体论述了相量图法求解正弦交流电路 的基本方法与技巧。
=关键词> 相量; 相量图; 正弦交流电路; 复阻抗 =中图分类号>O44 =文献标识码>3- 03
用相量图法分析正 弦交流 电路直 观、简洁, 甚至 有的 电路只能用相量图法进 行分析。但 要正 确地使 用相 量图 法, 必须掌握交流电路基本定律和构成交流电路最 基本的
图3
叠加。
2 复阻抗的定义及物理意义
2. 1 复阻抗的定义
电路如图 2 所示, 某一 元件其 端电 压为 ÛU, 流过 元件
图4
y =收稿日期>2005- 06- 20 =作者简介>林灵( 1973- ) , 女, 四川省德阳市人, 思茅师范高等专科学校计算机科学系讲师, 从事物理教育研究。
73

5A +
I?L A
3A
?
UR L
_
?
IR
O
I?
?
U
A
?
IL
B
?
?
?
I ? I L ? I R 由直角三角形 OBA得：
IL ?
I2
?
I
2 R
?
52 ? 32 ? 4A
电流表读数为 4A。
例题 4-15 ：定性画出 RLC 串联电路的相量图。
I?
+ U?–+R
U? U?–+L
– U?C–+
R jXL – jXC
弦交流电路中，不同的是电阻电路求解方程为实数 计算，正弦交流电路求解方程为复数运算。
例题4-27：已知 U?S ? 80? 00V ，f=50Hz ， 当 ZL 改变时，I?L 有效值不变，为 10A，试确定参数
?
U R3
?
U RL
?
IL
?
?
IR
IR
+
+
?
+
?
U_R3
R3
?
R1 U_R1
U?
U R2
?
U
A
RL
+? V U_ RL
R2
B+ ? U_ R2
?
?
UL
_
j? L
?
+
?
I L U_ L
U R1
?
?
U AB
?
?
U R3
?
U RL
IL
依据是：
?
?
U R3 ? R3 IL

根据相量图计算：
I I 2 I 12 202 102 17032A UR2 R 2 I 2 5 20 100 V UR2 UR2 100 UC 115.47 cos 2 I I 2 17.32 20 UX 2 U 2 C U 2 R2 115.472 1002 57.74V UC 115.47 XC 11.55 I1 10 UX 2 57.74 X2 2.89 I2 20 UR U UC 220 115.47 104.53V
U U U R C
因此得到直角三角形ＯＡＢ，所以
2 2 U UR UC 82 112 13.60V
电压表读数为 13.60V ．
得 此题的相量图也可按比例画出，用尺子量 U 的长度即为电压表读数．
U0V， （b）此电路图为ＲＬ并联电路，设电压 U I 90 且由ＫＣＬ得 I 考虑到 R 和 U 同相， L 滞后 U
U U U U R L C
U LU 可定性画出相量图如图4－36，当 时为图 C 超前 ，即 0 4－36（a）所示，这时 U 的相位为 的电路为感性电路；当 U LU C 时 I 0 ，为电阻性电路如图4－36（b）所示； U LU C 时， 0 ，为电容电路，如图4－36（c）所 示.
I R X 2 及 XC 。 求：
2200 同相，设 U 分析：由题中给出的条件 I 与U
为参考相量画相量图。
同相，且 C U U R 由相量图 R 与 U U 根据题意可知 I U
C 。在电容元件上 I1 超前U 2 I I ， C 90 ，且 I 可求得 U
1
1 及 I R 与 I 2 相同， 2 。在 R 2 上U 从而画出 I R 和 U X U C U R ，可画出 U X 。 又U

相量图法在电工技术中的应用摘要高等职业教育的人才培养目标是培养面向社会需求的高素质技能型人才,因此不论是专业课还是专业基础课,甚至是基础课都应紧紧围绕能力培养而进行。

本文主要阐述相量法在正弦交流电路分析、计算中的作用,探讨了如何应用相量图法在电工技术领域中的解决实际问题的思路及方法。

关键词电工技术;基础课程;相量法1 电工技术基础课程的教学应遵循高等职业教育的教学理念国家关于高等职业教育的培养目标十分明确,是“培养面向生产、建设、服务和管理第一线需要的高素质技能型专门人才。

”那么高职教育的人才培养规律应主动遵循适应社会发展需求,突出应用性和针对性,加强能力培养的原则。

因此,电工技术基础这门课程的教学理念应该在于培养学生分析问题解决问题的能力和方法。

2 正弦交流电的相量表示法正弦交流电在电工技术中处于重要位置,但交流电的分析却非常繁琐,正弦交流电的表示方法有3种:表达式法、波形图法、相量法。

这3种方法中相量法在交流电路的分析和计算中是最为便利的一种方法,也是应用最为广泛的一种方法。

正弦交流电的相量法有相量表示法和相量图法。

2.1 正弦交流电的相量表示法相量表示法注重问题的定量分析,利用数学的复数来表示。

交流电的相量表示法采用的是复数的极坐标形式。

从极坐标形式可以看出是由复数的模值及辐角来表示的一种方法。

当相量的模等于正弦量的最大值时,我们称其为最大值相量,以符号, , 表示;当相量的模等于正弦量的有效值时,我们称其为有效值相量,以符号, ,表示。

如电压的有效值相量用= 表示,其中U表示正弦交流电压的有效值, 表示正弦交流电压的初相角。

对于一个复杂的交流电路各分电压和总电压的关系可表示为:由此可见,交流电的相量表示法虽然采用了数学复数的极坐标形式,但在运算的过程中大量运用了数学的复数知识和复数的四则运算知识,这就要求学生掌握复数的这4种方法之间的相互转换。

这一方法对于数学基础较差的学生来说也显得非常困难。

电路知识：正弦交流电路与其分析方法“相量法”（上）“相量是什么？它和向量、矢量有什么区别？”，相信不少电工朋友都有着这样的疑问。

正如标题所示，相量是用于正弦交流电路分析的，换言之，离开正弦交流电路，相量将毫无意义。

而它与向量、矢量的区别，在看完本文后，你将能给出自己的答案。

掌握相量法，我们就可以快速并简单地对正弦交流电路进行分析、计算并理解其各种特性，包括电压电流、阻抗、有功功率以及无功功率等。

基于相量法的便捷性，本文将给大家详细讲解相量的含义以及运算，让大家学以致用，在交流电路分析中得心应手。

相量用于表示正弦交流电路中的各种正弦量，如电压、电流、磁通等。

所谓正弦量，是指电路中按正弦规律变化的各种物理量。

所以在理解相量前，我们有必要指定什么是正弦交流电路以及正弦量。

NO. 1正弦交流电路与正弦量电路有交流和直流之分，如下图1-1所示为不同形式的交流量和直流量波形图。

图1-1图（1）所示为恒定直流量的波形，例如电池的电压，在一定情况下就保持为恒定值。

而图（2）就是本文的主角，正弦交流量，即正弦量。

比较图1-1中的几种波形，可以发现，所谓直流量，不仅仅是指恒定直流量，还包括大小变化的各种时变量，如图（3）、图（6）的锯齿波，它们大小随时间变化，但方向保持不变，所以它们是直流量。

而交流，区别于直流，是指电路中的电压、电流等物理量方向发生变化，但大小不一定变化，例如图（4）的矩形波，该电流方向作周期变化，但其大小保持不变。

含有正弦电源且电路中各部分产生的电压、电流均按正弦规律变化的电路，就是正弦交流电路。

所谓正弦规律变化，正如图1-1中的图（2）所示。

在这里要说明一点，“正弦规律”不一定指正弦函数，其实余弦函数也是按正弦规律变化的，因为余弦函数可以由正弦函数左移90°得到。

所以上文提到的“正弦规律”指的是一种变化规律，而不是指正弦函数。

例如图1-2所示的电流和电压，都属于正弦量。

但在同一个电路中，一旦确定所用的函数，那么所有正弦量都应该用同一种函数表示，例如确定用sine正弦函数，就不能出现consine余弦函数，即使有，也应该根据三角函数换算转化为sine函数表示，这也是为了便于它们进行相位的比较。

３.ＫＣＬ和ＫＶＬ的相量形式 注意：第１点是相量图是否存在的主要依据，
第２ 、３点是如何正确画出相量图的主要依据．
二.用相量图法求解电路
１.参考相量的选择 （１）对于串联电路，选电流为参考相量 （２）对于并联电路，选电压为参考相量 （３）对于混联电路，参考相量选择比较灵活， 可根
据已知条件综合考虑 （４）较复杂的混联电路，常选末端电压或电 流为参考相量．
(b)设： U U0V， 先画出参考相量 U ，依据
Ｒ、Ｌ、Ｃ各元件电压电流相位关系，依次画出
可I分R 别、I定L 性、I画C 出相如量图，4由-36IL(a)I
C,IL
、(b)
IC及IL IC 三种情况 、(c)所示相量
图，最后电路ＫＣＬ方程 I IR IL IC
I IR IL
画出相量图如图4－35(b)所示．由直角三角形
ＯＡＢ可得
IL
I2

I
2 R

52 32 4A
电流表读数为４Ａ．
此题也可按比例用几何方法画出相量图，然后用量尺
测出 IL 的长度值即为电流表读数．
例 4-14 定性画出ＲＬＣ串联电路和ＲＬＣ并联电路的 相量图，它们的电路相量图模型如图4-36(a)和图
根据题意可知 I UR 与 U 同相，且UC U UR 由相量图
可求得 UC 。在电容元件上 I1 超前UC90，且 I2 I I1 ，
从而画出 I1 及 I2 。在 R2 上UR2与 I2 相同，
又 UX 2 UC UR2 ，可画出 UR2 和 UX 2 。
cos 2 I I 2 17.32 20
UX 2
U
2 C
U
2 R2

组成等边三角形。则
2 3 60
12 中北大学国家级电工电子实验教学示范中心
相量图分析例题演示3
此时可得
Z2 R2 jXL Z2 60 Z3 R3 jXC Z3 60
再利用功率的已知条件， 因为 I1=I2=I3；R1=R2=R3， 所以每个电阻上的功率相等， 则
P1
P2
P3
Uab Uan Ubn
由此可以得出如下结论：
9 中北大学国家级电工电子实验教学示范中心
位相图与相量图的关系
电压相量与电位相量是相互关联的。在复平 面上点的位置能确定该点的电位相量（指向 参考点），把点与点连接起来则确定了该两 点间的电压。反过来说一个电压相量的两个 端点对应着电路中的两个点，这两个点各有 其电位，电位相量箭头指向参考点。所以由 KVL的相量形式确定的的多边形闭合路径上， 任意两点间的电压都可以确定，把这两点连 接起来就是了，箭头应顺着你所表示的电压。
相量图分析例题演示3
[例3] 在图中已知U = 150V、50Hz；端口功率
P = 150W，且知I1 = I2 = I3；
R1 = R2 = R3 = R，试求各参数
解：因为I2=I3 所以 Z2 Z3
又因为 R2=R3，所以 XL=XC
则有
2 3
可见两支路阻抗互为共轭，
可画出相量图。
还因为I1=I2=I3，所以三电流可
cos
U
2 bd
U
2 ad
U
2 ab
1272
2202
1272
48400 0.866
2UadUab
2 220127 55880
2 中北大学国家级电工电子实验教学示范中心
相量图分析例题演示1

引言
模 为正弦量 的有效值 ， 则此相量称为有效值 相量。若这个 复 数 的模 为正 弦量 的最大值 ， 则此相量称 为最大值相量 。在 电 路分析 中 ， 我们通常用有效值 相量。正弦量 与相量 的对应关
系表示 为 ：
ｔ ｉ ｔ＋ Ｈ Ｉ＝ ｓ （ ｔ ） ＝ ｎｏ
＝
正弦交流 电可以用三角函数式和波形图来表 示 ， 由于在 进行交流 电路 的分析和计算时 ， 经常需要将几个频率相 同的 正弦量进行加减等运算 ， 这时若采用三角运算 和作 波形 图法 都不够方便 ， 因此正弦交 流 电常用相量来 表示 ， 这样 可 以把
相 量 图在分 析 正 弦交 流 电路 中的应 用
郭 山厚
（ 忻州师范学院 ， 山西 忻州 ０４ ０ ） ３ ００
摘 要： 相量 图法是分析正弦交流电路的一种重要方法， 中介绍 了相量、 文 相量图以及复 阻抗的基本定义和物理意义。具体论述了相量 图法在分析正弦交流电路稳 态、 态中的应用， 动
弦交流 电本身 是时 间 的正弦 函数 ， 相量 并不 等 于正 弦交 流
电。相量只是正 弦量进行 运算 时的一种表 示方法 和主要 工 具 。此外还要 明确 只有正弦交流 电才能用相量表示 ， 只有 同 频率 的正弦交流 电才能进行相量运算 。
１ ２ 相 量 图 ．
由于一个复数与复平 面 内的一个矢 量对应 ， 这样 ， 弦 正
１ 相量
１ １ 相 量 的 定 义 ．
Ｉｓ （ ｔ ） ， Ｉ 、 ＝ ｍｉ ｔ ＋ Ｈ ＝ ｍ ， ｎｏ
基尔 夫电 定 ∑“ ０ ｆ＝ 霍 压 律： ＝ 一∑ ， ０ 基尔 夫电 定 ∑ ０ 霍 流 律： ＝ 一∑ｊ ０ ＝
纯 电阻电路特性方程 ： ＝ 一 ｕ＝Ｉ ｔ Ｉ Ｒ

图4.45 例4.22图
先求其开路电压
U oc U SI Z L U S2 Z C ZL ZC
再求输出复阻抗
Z o Z C // Z L 1 Yo 1 YC Y L 1 jB C jB L
最后求电流 I3
I3 U oc Zo R

例4.23已知 I 10 0 A , G=1S,ωC=1S， L 试求图4.46所示电路中的 I 。
R ZC
ZC

Uo
G Ui G
2
2
C
2
2 2
2
j 3G C
2
G C
0
1 RC
o

G C

Uo
G Ui j 3G C

2

Ui j3
j
Ui 3

Ui 3
90
4.8.3 用代文宁定理分析正弦电路 例 4.22 用代文宁定理计算例4.20中R支路的电流 。
i C ( t ) 11 . 3 2 sin( 3000 t 98 ) mA i L ( t ) 25 . 3 2 sin( 3000 t 55 . 4 ) mA
例 ４.18 图4.41(a)所示的电路中, 端口电压 u cd ( t ) 100
R1 X L , R 2 X C
的性质，作出UC 相量。由KVL给出U1=UC+U2 的关系及
U1=U2的条件作出端口电压U1的相量。特别注意U1的位
置。由相量图可知
IC I I L 10
2 2
2A U C
2 U 1 200
2V