- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•状态方程和输出方程的一般形式
u(t)
k
x(t) f(x(t),u(t),t) m
y(t)g(x(t),t)
y
例1 质量—弹簧—阻尼系统
fy’ ky
d2y(t) d(y t) m b k(yt)u(t)
dt dt
设
x1
y,x2
dy(t) dt
m
u(t) y
14
1-1 状态变量及状态空间表达式
m x2 bx 2 kx1 u (t ) x1 x2
LddtiRiuc u(t)
duc i / C dt
ddtiR LiL 1ucu(t)
令 x1i,x2uc 16
1-1 状态空间表达式
线性系统状态方程和输出方程的一般形式
x A(t)xB(t)u y C(t)xD(t)u
状态方程 输出方程
单输入输出线性定常系统
x Ax bu b,为列向量
y Cx du c为行向量
x 2
b m
x2
k m
x1
1 m
u (t )
给定: x1(0 )x ,2(0 )u ,(t)t,0
y x1
x1
x2
0
k m
1 b
m
x1 x2
0
1
m
u
y 1
0
x1 x2
15
1-1 状态变量及状态空间表达式
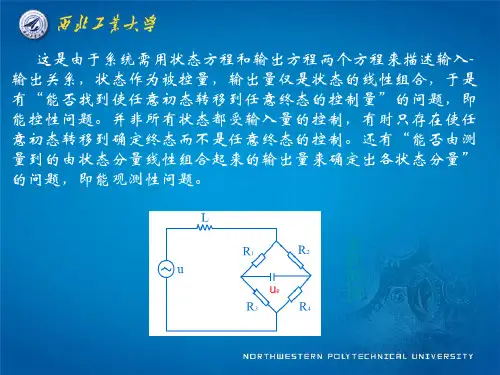
RLC电路 电容电压和电感电流
RL i
u(t)
uc(t)
C duc i dt
d为标量
17
1-1 状态空间表达式
x A(t)xB(t)u y C(t)xD(t)u
多输入多输出线性定常系统
写出2输入1输出系统 的B,C,D的一般形式
x :n 1 u :r1 y: p1
A :n n B :n r C :pn D :pr
A11 A12 A13
A
A21
A22
A32
A31 A32 A33
7
0-4 现代控制理论的应用
宇宙飞船 电力系统(发电和用户) (生产管理控制问题)
高性能飞机(F16,苏27-苏30)
广泛应用: 现代化仪表(完备的传感器和执行器) 与便 宜的电子硬件和控制理论处理动态系统的能力 各种运动控制卡,模块化的传感器,各种处理芯片(无线 通讯模块,光电码盘,雷达)
8
第一章 控制系统的状态空间表达式
x 1 x 1
k
x 2 x 2
20
1-2 状态空间表达式的模拟结构图
模拟结构图: 系统中各状态变量之间的信息传递关系
x1
x2
0
k m
1 b
m
x1 x2
0
1
m
u
y 1
0
x1 x2
k./m
u
1/m
x 2
x 1 x2
x1
1
y
b/m
21
1-2 状态空间表达式的模拟结构图
由状态变量x和输入变量u的描述的一阶微分方程组
x (t)f(x(t)u ,(t))
状态变量x和输出变量y的函数关系
在给定当前状态、激励和系统动态 方程的条件下,状态变量描述了系
统的未来响应 输入 u(t)
x(0)
动态系统 x1, x2, …, xn
状态 x(t)
输出 部件
输出y(t)
13
1-1 状态空间表达式
10
第一章 控制系统的状态空间表达式
状态矢量 状态空间
x(t) [x 1 (t)x ,2(t),x .n(.t).T ]
以状态变量为坐标轴所构成的n维空间,称为状态空间
状态轨迹 (help plot3)
11
第一章 控制系统的状态空间表达式
状态空间
12
第一章 控制系统的状态空间表达式
状态方程
+输出方程
其数学描述就是反映系统变量间因果关系和变换的一种 数学模型(时域) 状态空间表达式
1-1 状态变量及状态空间表达式 •状态变量
完全表征系统运动状态, 具有最小个数的一组变量.
例如:要表示一维受力运动的质点运动.
位置,速度, ma=F
mx f
9
第一章 控制系统的状态空间表达式
在平坦道路上行驶的汽车的状态? 对于n阶系统,有n个独立的状态变量. 状态变量的选择不是唯一的.
传递函数
复杂系统:系统内部的结构特性
5
0-1 控制理论的性质
性能指标的多样性 性能指标 在一段时间上的所需性能和实际性能的差 异的性能指标, 控制的目标是寻找一个使性能指标为 最小的时间函数的控制. 时间最小 燃料最小
6
0-2 控制理论的发展
20世纪50年代到60年代 极大值原理, 动态规划, 维纳和卡尔曼滤波 计算机的发展 对系统进行完全的描述: 状态空间表达式 能控性,能观性,状态实现,线性二次型最优控制 成为整个控制理论发展的概念基础
18
1-1 状态空间表达式的系统框图
状态空间描述的系统信号传递的关系图
D
u
B
x x
C
y
A
线性系统框图(方块图)
19
1-2 状态空间表达式的模拟结构图
模拟结构图: 系统中各状态变量之间的信息传递关系
一 维 状态空间 x 5 x 2u y 3x 8u
积分器、比例器、求和器
二 维 状态空间 x1 5 x 2 2 u x 2 x1 3 x 2 u y 3 x1 7u
114
3
线性控制系统的能控 性和能观测性
6
4 系统稳定性
3
118 14
5 线性定常系统的综合 4 2 1 1 8
总复习与机动
2 4
0-1 控制理论的性质
动态和稳态性能
R(S) E(S)
GC(S)
N(S)
Y(S)
G(S)
H(S)
•系统输入-输出的数学描述: •系统性能的提高: 反馈控制和基于反馈的串联校正
练习: 写出矩阵形式, 画出下列系统的模拟结构图
d
x1 a11x1 a12x2 b1u1; u1
x2 a22x2 b2u2
b1
x 1
x1
c1
y
y c1x1 c2x2 du1
a11
a12
u2
b2
x 2
x2
c2
a22
22
1-3 状态空间表达式的建立(1)
如何获得状态空间描述 •物理系统的机理(电气,机械,机电,气动等)
2
参考文献
1 《现代控制理论》 (第3版) ,
2
刘豹,机械工业出版社
2 《现代控制理论基础》,
谢克明 ,北京工业大学出版社
3 《现代控制理论基础》 ,
曲延滨等 ,哈尔滨工业大学
3
现代控制理论学时分配
章节
主要内容
0 绪论
各教学环节学时分配
讲实讨习小 授验论题计
1
1
备注
1 状态空间描述
4
15
2 线性系统的时域分析 2
现代控制理论
0 绪论 1 控制系统的状态空间表达式 2 状态空间表达式的解 3 线性控制系统的能控性和能观性 4 稳定性分析 5 线性定常系统的时域综合
1
整体概述
概况一
点击此处输入相关文本内容 点击此处输入相关文本内容
概况二
点击此处输入相关文本内容 点击此处输入相关文本内容
概况三
点击此处输入相关文本内容 点击此处输入相关文本内容