电阻应变片例题与练习题

课堂练习卷（二）姓名：
一、填空（42%）：
1.能将被测 (如应变、温度、湿度等)的变化转换成的变化的装置，称为电阻式传感器。

2.导电材料的电阻不仅与材料的、有关，还与、和等因素有关。

3.常用的有电阻应变式传感器、传感器、电阻传感器、电阻传感器、电阻传感器、电阻传感器等。

4.电阻应变式传感器是利用电阻应变片受后发生致使发生变化
的原理，来测量被测物理量的大小。

5. 应变片根据所使用的材料不同，可分为应变片和应变片两大类。

6. 利用电阻应变原理制成的传感器可用来测量诸如、、等参数。

7. Resistance strain-gage transducter的中文是。

二、选择填空（18%）
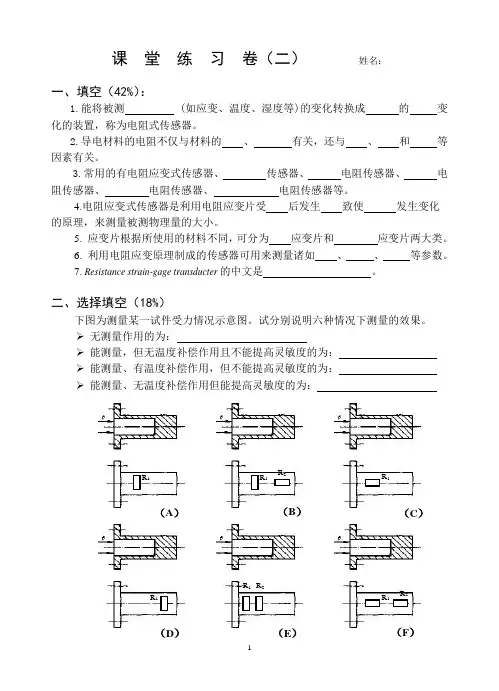
下图为测量某一试件受力情况示意图。

试分别说明六种情况下测量的效果。

➢无测量作用的为：
➢能测量，但无温度补偿作用且不能提高灵敏度的为：
➢能测量、有温度补偿作用，但不能提高灵敏度的为：
➢能测量、无温度补偿作用但能提高灵敏度的为：
R1R1R2R
1
R1R2
R1
R2 R1
（A）（B）（C）（D）（E）（F）
1
三、问答题：
1.画出电桥测量电路，并分别说明四种不同的应用（要写出应用的名称和对应的输入输出关系式）。

（25%）
2.右图是应变式加速度传感器的原理图，说明其工作原
理，并指出该测量方法是否有温度补偿作用、能否提高灵敏
度。

（15%）
返回
2。

第3章应变式传感器概述1．什么是应变效应？什么是压阻效应？什么是横向效应？试说明金属应变片与半导体应变片的相同和不同之处。

2．有一吊车的拉力传感器如图所示，电阻应变片R1、R2、R3、R4等截面轴上，已知R1—R4标称阻值为120Ω，桥路电压2V，物重m引起R1、R2变化增量为1.2Ω。

请画出应变片电桥电路，计算出测得的输出电压和电桥输出灵敏度，R3、R4起什么作用？8. 说明电阻应变片的组成和种类。

电阻应变片有哪些主要特性参数？9. 一个量程为10kN的应变式测力传感器，其弹性元件为薄壁圆筒轴向受力，外径20mm,内径18mm,在其表面粘贴八各应变片，四个沿周向粘贴，应变片的电阻值均为120Ω,灵敏度为2.0,波松比为0.3,材料弹性模量E=2.1×1011Pa。

要求：①绘出弹性元件贴片位置及全桥电路；②计算传感器在满量程时，各应变片电阻变化；③当桥路的供电电压为10V时，计算传感器的输出电压。

10. 应变片产生温度误差的原因及减小或补偿温度误差的方法是什么？11. 今有一悬臂梁，如图所示，在其中上部上、下两面各贴两片应变片，组成全桥，该梁在其悬臂梁一端受一向下力F=0.5N,试求此时这四个应变片的电阻值。

已知：应变片灵敏系数K=2.1;应变片空载电阻R0=120Ω。

12. 如图所示一受拉的10#优质碳素钢杆。

试用允许通过的最大电流为30mA的康铜丝应变片组成一单臂受感电桥。

试求出此电桥空载时的最大可能的输出电压（应变片的电阻为120Ω）。

13．钢材上粘贴的应变片的电阻变化率为0.1%，钢材的应力为10kg/mm2。

①求钢材的应变。

②钢材的应变为300*10-6时，粘贴的应变片的电阻变化率为多少?14．截面积为1mm2、长度为100m铜线的电阻为多少？具有和它相同电阻的100m铝线的截面积为多大？比较此时的铝线重量和铜线重量。

答案7. 解：8.答：① 金属电阻应变片由四部分组成：敏感栅、基底、盖层、粘结剂、引线。

K u n m i n g U n i v e r s i t y o f S c i e n c e a n d T e c h n o l o g yF a c u l t y o f M e c h a n i c a l a n d E l e c t r i cG u o Y u3-3电阻丝应变片与半导体应变片在工作原理上有何区别？各有何优缺点？应如何针对具体情况来选用？答：电阻丝应变片的工作原理是利用导体形变引起阻值的变化（金属应变效应）；而半导体应变片是利用半导体电阻率变化引起电阻的变化（压阻效应）。

金属应变片的优点包括：制作方便，温度稳定性和可重复性好等；主要缺点：灵敏度低，横向效应等；半导体应变片的优点包括：灵敏度高，机械滞后小，横向效应小和体积小等；主要缺点：温度稳定性差、灵敏度系数非线性大。

选用略。

3-4 有一电阻应变片（见图3-84），其灵敏度S g =2，R=120Ω，设工作时其应变为1000με，问△R=？设将此应变片接成图中所示的电路，试求：1)无应变时电流表示值；2）有应变时电流表示值；3)电流表示值相对变化量；4）试分析这个变量能否从表中读出？解：Ω=××==Δ⇒=Δ−24.01201023R S R S RRg g εε 1） 无应变时 mA R U I 5.121205.11===2） 有应变时mA R R U I 475.1224.01205.12≈+=Δ+=3） 电流表示值相对变化量mA I I I 025.0475.125.1221=−=−=Δ4) 普通毫安表量程选10mA ，设精度为满量程的0.01%，则不能从表中正确读出。

4-1 以阻值R=120Ω、灵敏度S g =2的电阻丝应变片与阻值为120Ω的固定电阻组成电桥，供桥电压为3V ，假定负载电阻为无穷大，当应变片的应变为2με和2000με时，分别求出单臂、双臂电桥的输出电压，并比较两种情况下的电桥灵敏度。

1、一应变片的电阻R0=120Ω，K=2.05，用作应变为800μm/m的传感元件。

(1)求△R与△R/R； (2)若电源电压Ui=3V，求其惠斯通测量电桥的非平衡输出电压U0。

解：(1)△R/R=Kε=2.05x800μm/106μm=1.64x10-3则△R=1.64x10-3 x R=1.64x10-3 x 120Ω=0.197Ω(2)2、如果将 120Ω的应变片贴在柱形弹性试件上，该试件的截面积 S=0.5×10-4m2，材料弹性模量 E=2×1011N/ m2。

若由5×104N的拉力引起应变片电阻变化了 1.2Ω，求该应变片的灵敏系数 K。

解：△R/R=1.2/120=0.01K=△R/R/ε=23、以阻值R=120Ω，灵敏系数 K=2.0的电阻应变片与阻值 120Ω的固定电阻组成电桥，供桥电压为3V，并假定负载电阻为无穷大，当应变片的应变为 2με和2000με时，分别求出单臂、双臂差动电桥的输出电压，并比较两种情况下的灵敏度。

解：单臂：双臂：电压灵敏度：4、在材料为钢的实心圆柱试件上，沿轴线和圆周方向各贴一片电阻为 120Ω的金属应变片R1和R2，把这两应变片接入差动电桥。

若钢的泊松比μ=0.285，应变片的灵敏系数 K=2，电桥的电源电压Ui=2V，当试件受轴向拉伸时，测得应变片R1的电阻变化值△R=0.48Ω，试求电桥的输出电压 U；若柱体直径d=10mm，材料的弹性模量E=2×1011N/ m2，求其所受拉力大小。

解：由则=所以电桥输出电压为当柱体直径d=10mm时，由，得5、某120Ω电阻应变片的额定功耗为40mW，如接人等臂直流电桥中，试确定所用的激励电压。

解：由电阻应变片R=120Ω，额定功率P=40mW，则其额定端电压为，当其接入等臂电桥中时，电桥的激励电压为。

第四章 传感器原理习题4-1以阻值R =120Ω，灵敏系数K =2.0的电阻应变片与阻值120Ω的固定电阻组成电桥，供桥电压为3V ，并假定负载电压为无穷大，当应变片的应变为2με和2000με时，分别求出单臂、双臂差动电桥的输出电压，并比较两种情况下的灵敏度。

4-2 在材料为钢的实心圆柱试件上，沿轴线和圆周方向各贴一片电阻为Ω120的金属应变片R 1和R 2，把这两片应变片接入差动电桥(题图4-2)。

若钢的泊松比μ=0.285，应变片的灵敏系数K =2，电桥的电源电压U i=2V ，当试件受轴向拉伸时，测得应变片R 1的电阻变化值∆R =0.48Ω，试求电桥的输出电压U 0；若柱体直径d =10mm ，材料的弹性模量211N/m 102E ⨯=，求其所受拉力大小。

题图4-2 差动电桥电路4-3 一台采用等强度的梁的电子称，在梁的上下两面各贴有两片电阻应变片，做成称重量的传感器，如习题图4-3所示。

已知l =10mm ，b 0=11mm ，h =3mm ， 24N/mm 102.1E ⨯=，K =2，接入直流四臂差动电桥，供桥电压6V ，求其电压灵敏度(K u=U 0/F)。

当称重0.5kg 时，电桥的输出电压U 0为多大?题图4-3悬臂梁式力传感器4-4 有四个性能完全相同的应变片(K =2.0)，将其贴在习题图4-4所示的压力传感器圆板形感压膜片上。

已知膜片的半径R =20mm ，厚度 h =0.3mm ，材料的泊松比μ=0.285，弹性模量211N/m 102E ⨯=。

现将四个应变片组成全桥测量电路，供桥电压U i=6V 。

求：(1)确定应变片在感压膜片上的位置，并画出位置示意图；(2)画出相应的全桥测量电路图；(3)当被测压力为0.1MPa 时，求各应变片的应变值及测量桥路输出电压U 0；(4)该压力传感器是否具有温度补偿作用?为什么?(5)桥路输出电压与被测压力按是否存在线性关系?题图4-4 膜片式压力传感器4-5一测量线位移的电位器式传感器，测量范围为0~10mm ，分辨力为0.05mm ，灵敏度为2.7V/mm ，电位器绕线骨架外径d =0.5mm ，电阻丝材料为铂铱合金，其电阻率为mm Ω103.25ρ4⋅⨯=-。

第二部分：填空题
1、测量弹性模量和泊松比时，在试件两侧粘贴电阻应变片是为了消除上下夹具不在垂直线上，试件不直等的影响。

2、采用等量加载的目的是验证力和形变之间的关系，从而验证胡克定律。

3、电阻应变片横向效应系数H是指横向灵敏系数与纵向敏系数之比值，用横向百分数表示。

4、电阻应变片的灵敏系数是指安装在被测构件上的电阻应变片，在其轴向受到单向应力时引起的电阻相对变化与由此单向应力引起的试件表面轴向应变之比。

5、设置温度补偿块必需满足的3个基本条件是：(1)补偿块与试件的_材料_相同，且不_受力；(2)粘贴于其上的补偿应变片和工作应变片处于_同一温度_环境下；(3)补偿应变计与工作应变片应是_同一批次应变片。

6、根据平面应变状态分析，测点任意2个互相垂直方向上的线应变之和等于该测点最大与最小主应变之和。

7、梁一端固定，另一端受可沿轴线滑动的铰支座约束。

当环境温度升高时，梁上各点的应力为零，应变增大。

8、一般常用的电阻应变片种类有丝绕式、箔式和半导体式。

9、电阻应变仪的测量原理为应变电桥电路、电压或电流放大电路、数据显示电路。

10、电桥的接桥方式一般分为四分之一桥、半桥、全桥。

11、电阻应变仪的示值读数为微应变。

第二章电阻式传感器原理与应用[基本要求]1. 掌握金属应变式传感器的构成原理特性；2. 掌握压阻式传感器工作原理，固态压阻器件设计特点；3. 了解电阻应变式传感器动的粘贴方法；4. 通过对电阻应变片测量电路分析，掌握直流惠斯通电桥结构形式及特点。

[例题分析]例题2-1 如果将100Ω电阻应变片贴在弹性试件上，若试件受力横截面积S = 0.5×10-4 m 2，弹性模量E =2×1011 N/m 2 ，若有F=5×104 N 的拉力引起应变电阻变化为1Ω。

试求该应变片的灵敏度系数？解：由题意得应变片电阻相对变化量1001=∆R R 根据材料力学理论可知：应变Eσε=（σ为试件所受应力，SF =σ），故应变 005.0102105.01051144=⨯⨯⨯⨯=⋅=-E S F ε应变片灵敏度系数2005.0100/1/==∆=εRR K 例题2-2 一台用等强度梁作为弹性元件的电子秤，在梁的上、下面各贴两片相同的电阻应变片(K=2）如图2-1（a)所示。

已知l =100mm 、b=11mm 、t=3mm ，E=2×104N/mm 2。

现将四个应变片接入图（b ）直流电桥中，电桥电压U=6V 。

当力F=0.5kg 时，求电桥输出电压U 0=?解： 由图（a ）所示四片相同电阻应变片贴于等强度梁上、下各两片。

当重力F 作用梁端部后，梁上表面R 1和R 3产生正应变电阻变化而下表面R 2和R 4则产生负应变电阻变化，其应变绝对值相等，即Ebt Fl242316==-=-==εεεεε 电阻相对变化量为ε⋅=∆=∆-=∆-=∆=∆K RRR R R R R R R R 44223311 现将四个应变电阻按图（b ）所示接入桥路组成等臂全桥电路，其输出桥路电压为mV V Ebt FlK U K U R R U 8.170178.01023111008.95.06264220==⨯⨯⨯⨯⨯⨯⨯⨯=⋅⋅=⋅=⋅∆=εε例题2-3采用四片相同的金属丝应变片(K =2），将其贴在实心圆柱形测力弹性元件上。

习题集及答案第3章 电阻应变式传感器3.5 一应变片的电阻R=120Ω，灵敏系数k =2.05，用作应变为800/m m μ的传感元件。

求：①R ∆和/R R ∆；② 若电源电压U =3V ，初始平衡时电桥的输出电压U 0。

3.6 在以钢为材料的实心圆柱形试件上，沿轴线和圆周方向各贴一片电阻为120Ω的金属应变片R 1和R 2（如图3-28a 所示），把这两应变片接入电桥（见图3-28b ）。

若钢的泊松系数0.285μ=，应变片的灵敏系数k =2，电桥电源电压U =2V ，当试件受轴向拉伸时，测得应变片R 1的电阻变化值10.48R ∆=Ω。

试求：①轴向应变；②电桥的输出电压。

3.9 图3-31为一直流电桥，负载电阻R L 趋于无穷。

图中E=4V ，R 1=R 2=R 3=R 4=120Ω，试求：① R 1为金属应变片，其余为外接电阻，当R 1的增量为ΔR 1=1.2Ω时，电桥输出电压U 0=? ② R 1、R 2为金属应变片，感应应变大小变化相同，其余为外接电阻，电桥输出电压U 0=? ③ R 1、R 2为金属应变片，如果感应应变大小相反，且ΔR 1=ΔR 2 =1.2Ω，电桥输出电压U 0=?答案3.5解：2.05;800/k m m εμ==/0.0164;0.2R R k R ε∴∆=⋅=∆≈Ω应变引起的电阻变化033 1.234R U V U mV R ∆==⋅=当电源电压时，电桥输出电压3.6解1：1）11/R R k ε∆= 则轴向应变为：1/0.48/1200.0022R R k ε∆=== 2）电桥的输出电压为：011(1)220.002 1.285 5.1422U Uk mV εμ=+=⨯⨯⨯⨯=解2：112;120;0.48;2k R R U V ==Ω∆=Ω=1101142R R k U U R R mV ε∆==⋅∆=/轴向应变： 0.002电桥输出电压： / 3.9解: ①100.0104E R R U V R ∆=⋅=因为只有为应变片,电桥输出按单臂电桥计算， ②00U V =因为两应变片变化大小相同，相互抵消无输出， ③120,0.022E R R R U V R ∆=⋅=因为应变时大小变化相反,电桥输出按半桥计算，。

一、填空题1、应变仪的灵敏度系数12.30K=，应变片的灵敏度系数2 2.06K=，仪器的读数是1400εμε=，则实际的应变值是ε=（）。

2、在进行电测试验时，若将两个电阻值相等的工作片串联在同一桥臂上，设两个工作片的应变值分别为ε1、ε2，则读数应变（）3、当应变计与应变仪连接的导线较长时，例如大于50 m以上，由于导线本身有一定电阻值，它和应变计一起串联在应变电桥的桥臂上而又不参加变形，这将使指示应变小于真实应变，可以通过改变应变仪的来修正。

4、有一粘贴在轴向受压试件上的应变片，其阻值为Ω120，灵敏系数136.2=K。

问：当试件上的应变为με1000-时，应变片阻值是多少？5、工程测量中，应变电桥的接法有_______________、_______________和_______________等几种。

6、应变计的主要技术参数是_______________、_______________和_______________等。

7、工程结构应变测量中，常用的温度补偿有___________补偿法和___________补偿法两种。

8、设置温度补偿块必需满足的3个基本条件是：(1)补偿块与试件的_____________相同，且不_____________；(2)粘贴于其上的补偿应变计和工作应变计处于_____________环境下；(3)补偿应变计与工作应变计应是_____________应变计。

9、应变仪的灵敏度系数K仪=2.08，应变片的灵敏度系数K片= 2.00，当仪器的读数ε=400με，则实际的应变值ε为。

仪10、一般常用的电阻应变片种类有（）、（）和（）。

二、选择题1、圆轴受扭矩T的作用，用应变片测出的是（ )。

A. 剪应变Ｂ．剪应力Ｃ．线应变Ｄ．扭矩2、电阻应变片的灵敏度系数K指的是（)。

A. 应变片电阻值的大小B. 单位应变引起的应变片相对电阻值变化C. 应变片金属丝的截面积的相对变化D. 应变片金属丝电阻值的相对变化3、用惠斯登电桥测量纯弯曲梁应变时，当温度补偿应变片所贴的构件材料的线膨胀系数小于被测梁的线膨胀系数时，应变测量结果与真实结果（）。

传感检测技术例题第一章传感检测技术例题1.01、传感器的一般特性1.02、电阻式传感器例1、一只应变片的电阻R=120Ω，灵敏度系数K=2.05，用做应变ε=800μm/m 的传感元件，将其接入等臂电桥。

求：（1）、ΔR和ΔR/R；（2）、若电源电压U=3V，惠斯登电桥的输出电压U0为多大？解：（1）、应变片的电阻相对变化量为：ΔR/R=Kε=2.05×800×10-6；=1.64×10-3=0.164℅应变片的电阻变化量为：ΔR=R×ΔR/R=120×0.164℅=0.197Ω（2）、惠斯登电桥的输出电压为：U0=U×ΔR/4R=(1/4)×0.164℅×3=1.23mV例2、在以钢为材的实心圆柱形试件上，沿轴线和圆周方向个各贴一片电阻为120的金属应变片R1和R2，如图所示。

把这两个应变片接入电桥，如图所示。

如果钢的泊松系数μ=0.285,应变片的灵敏度系数K=2，电桥电源电压U=2V,当试件受到轴向拉伸时，测得应变片R1的电阻变化值ΔR1=0.48Ω。

求：（1）、轴向应变量。

（2）、电桥的输出电压。

解：(1)、根据：ΔR/R=Kε轴向因变量为：ε=ΔR1/R1K=0.48/(120×2)=0.002=2000με（2）、根据泊松效应，圆柱的周向应变为：εr=-με=-0.285×2000=-570με故：ΔR2=Kεr R2=-2×570×10-6×120=-0.137Ω电桥输出电压：U0=(1/4)( ΔR1/R1-ΔR2/R2)U=(1/4)×(0.48/120+0.137/120)×2=2.57mV例3、一个测量吊车起吊重物时拉力的传感器如图1.6（a）所示，将R1、R2、R3、R4按要求贴在等截面轴上。

已知等截面轴的横截面面积A=0.00196m2,材料的弹性模量E=2×1011N/m2,泊松比μ=0.3，且R1=R2=R3=R4=120Ω,K=2,所组成的全桥电路如图1.6（b）所示，电桥供电电压U=2V.。

浙江大学电气工程学院现代传感器技术赵梦恋，吴晓波 2008-2009学年冬学期2008年12月二、电阻应变式传感器（2） 习 题2-1一丝绕应变计的灵敏系数为2，初始阻值100Ω，试求当试件受力后的应变为31.810-⨯时该应变计的电阻变化ΔR。

答：Ω=⨯⨯⨯=⋅⋅=∆-36.0108.121003εK R R2-2一试件受力后的应变为3102-⨯；丝绕应变计的灵敏系数为2，初始阻值120Ω，温度系数C ο61050-⨯-，线膨胀系数为C ο61014-⨯；试件的线膨胀系数为C ο61012-⨯。

试求：温度升高20℃时，应变计输出的相对误差和相对热输出。

答：()t S t Ra t K t Rββ∆=∆+-⋅∆ =()C C C C οοοο20101410122201050666⨯⨯-⨯⨯+⨯⨯----=31008.1-⨯-()43104.521008.1/--⨯-=⨯-=∆=KR R tt ε2-3在悬臂梁的上下方各贴一片电阻为120Ω的金属应变片R 1和R 2。

若应变片的灵敏系数k =2，电源电压U =2V ，当悬臂梁顶端受到向下的力F 时，电阻R 1和R 2的变化值ΔR 1 =ΔR 2 =Ω，试求电桥的输出电压。

答：A1R2120124R R U U R R ⎛⎫∆∆∆=-⎪⎝⎭20.480.4844120120mV ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦解析：参见PPT P23~24，关于电阻应变计的测量电路。

理解电桥的测量原理和计算方法。

2-4图为一直流应变电桥，图中U =4V ，1234120R R R R ====Ω，试求：① 1R 为金属应变片，其余为外接电阻，当1R 的增量为1 1.2R ∆=Ω时，电桥输出电压U O 。

② 1R 、2R 都是应变片，且批号相同，感应应变的极性和大小都相同，其余为外接电阻，电桥输出电压U O 。

③ 题②中，如果2R 与1R 的感受应变的极性相反，且12 1.2R R ∆=∆=Ω，电桥输出电压U O 。

二、电阻应变式传感器（二）习 题2-1.一试件受力后的应变为3102-⨯；丝绕应变计的灵敏系数为2，初始阻值120Ω，温度系数C61050-⨯-，线膨胀系数为C 61014-⨯；试件的线膨胀系数为C 61012-⨯。

试求：温度升高20℃时，应变计输出的相对误差。

答：()t S t Ra t K t Rββ∆=∆+-⋅∆ =()C C C C20101410122201050666⨯⨯-⨯⨯+⨯⨯---- =31008.1-⨯-2-2. 在悬臂梁的上下方各贴一片电阻为120Ω的金属应变片R 1和R 2。

若应变片的灵敏系数k =2，电源电压U =2V ，当悬臂梁顶端受到向下的力F 时，电阻R 1和R 2的变化值ΔR 1 =ΔR 2 =Ω，试求电桥的输出电压。

答：A1R2120124R R U U R R ⎛⎫∆∆∆=- ⎪⎝⎭20.480.4844120120mV ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦解析：参见PPT P23~24，关于电阻应变计的测量电路。

理解电桥的测量原理和计算方法。

2-3.图为一直流应变电桥，图中U =4V ，1234120R R R R ====Ω，试求：① 1R 为金属应变片，其余为外接电阻，当1R 的增量为1 1.2R ∆=Ω时，电桥输出电压U O 。

② 1R 、2R 都是应变片，且批号相同，感应应变的极性和大小都相同，其余为外接电阻，电桥输出电压U O 。

③ 题②中，如果2R 与1R 的感受应变的极性相反，F A且12 1.2R R ∆=∆=Ω，电桥输出电压U O 。

答：①31241123414 1.210444120O R R R R R U U U mV R R R R R ⎛⎫∆∆∆∆∆∆=-+-==⨯= ⎪⎝⎭ 或者更精确地()()()()()()1132411234120 1.212012012049.95120 1.2120120120O R R R R R U U mV R R R R R +∆-+-⨯=⋅=⨯=+∆+++++或者()411311011241113111111R R R R R R U U UR R R R R R R R ∆∆==⎛⎫⎛⎫⎛⎫∆∆++++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=② 312412123412044O R R R R R R U U U V R R R R R R ⎛⎫⎛⎫∆∆∆∆∆∆∆=-+-=-= ⎪ ⎪⎝⎭⎝⎭或者3110112234R R R U U R R R R R R ⎛⎫∆+=- ⎪∆+++∆+⎝⎭=0V③3124121234124 1.2 1.220444120120O R R R R R R U U U mVR R R R R R ⎛⎫⎛⎫∆∆∆∆∆∆⎛⎫⎛⎫∆=-+-=-=--= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭或者 3110112234R R R U U R R R R R R ⎛⎫∆+=-⎪∆++-∆+⎝⎭=解析：参见PPT P23~27，关于电阻应变计的测量电路。