数字信号处理第三章-2
- 格式:ppt
- 大小:808.50 KB
- 文档页数:28




数字信号处理(方勇)第三章习题答案3-1 画出)5.01)(25.01()264.524.14)(379.02()(211211------+--+--=z zz z z z z H 级联型网络结构。
解:23-2 画出112112(23)(465)()(17)(18)z z z H z z z z --------+=--+级联型网络结构。
解:()x n ()y n 243-3 已知某三阶数字滤波器的系统函数为1211252333()111(1)(1)322z z H z z z z -----++=-++,试画出其并联型网络结构。
解:将系统函数()H z 表达为实系数一阶,二阶子系统之和,即:()H z 11122111111322z z z z ----+=+-++ 由上式可以画出并联型结构如题3-3图所示:)题3-3图3-4 已知一FIR 滤波器的系统函数为121()(10.70.5)(12)H z z z z ---=-++,画出该FIR 滤波器的线性相位结构。
解: 因为121123()(10.70.5)(12)1 1.30.9H z zz z z z z ------=-++=+-+,所以由第二类线性相位结构画出该滤波器的线性相位结构,如题3-4图所示:()x n 1-1-1z -题3-4图3-5 已知一个FIR 系统的转移函数为:12345()1 1.25 2.75 2.75 1.23H z z z z z z -----=+--++求用级联形式实现的结构流图并用MATLAB 画出其零点分布及其频率响应曲线。
解: 由转移函数可知,6=N ,且)(n h 偶对称,故为线性相位系统,共有5个零点,为5阶系统,因而必存在一个一阶系统,即1±=z 为系统的零点。
而最高阶5-z 的系数为+1,所以1-=z 为其零点。
)(z H 中包含11-+z 项。
所以:11()()(1)H z H z z -=+。
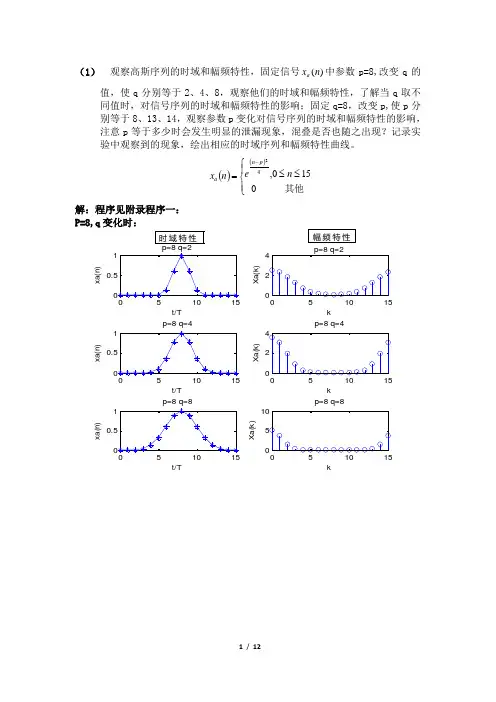
(1) 观察高斯序列的时域和幅频特性,固定信号)(n x a 中参数p=8,改变q 的值,使q 分别等于2、4、8,观察他们的时域和幅频特性,了解当q 取不同值时,对信号序列的时域和幅频特性的影响;固定q=8,改变p,使p 分别等于8、13、14,观察参数p 变化对信号序列的时域和幅频特性的影响,注意p 等于多少时会发生明显的泄漏现象,混叠是否也随之出现?记录实验中观察到的现象,绘出相应的时域序列和幅频特性曲线。
()()⎪⎩⎪⎨⎧≤≤=-其他0150,2n e n x q p n a解:程序见附录程序一:P=8,q 变化时:t/T x a (n )k X a (k )t/T x a (n )p=8 q=4k X a (k )p=8 q=4t/Tx a (n )p=8 q=8kX a (k )p=8 q=8幅频特性时域特性t/T x a (n )p=8 q=8k X a (k )p=8 q=8t/T x a (n )51015k X a (k )p=13 q=8t/Tx a (n )p=14 q=851015kX a (k )p=14 q=8时域特性幅频特性分析:由高斯序列表达式知n=p 为期对称轴; 当p 取固定值时,时域图都关于n=8对称截取长度为周期的整数倍,没有发生明显的泄漏现象;但存在混叠,当q 由2增加至8过程中,时域图形变化越来越平缓,中间包络越来越大,可能函数周期开始增加,频率降低,渐渐小于fs/2,混叠减弱;当q 值固定不变,p 变化时,时域对称中轴右移,截取的时域长度渐渐地不再是周期的整数倍,开始无法代表一个周期,泄漏现象也来越明显,因而图形越来越偏离真实值,p=14时的泄漏现象最为明显,混叠可能也随之出现;(2) 观察衰减正弦序列 的时域和幅频特性,a=0.1,f=0.0625,检查谱峰出现的位置是否正确,注意频谱的形状,绘出幅频特性曲线,改变f ,使f 分别等于0.4375和0.5625,观察这两种情况下,频谱的形状和谱峰出现的位置,有无混叠和泄漏现象?说明产生现象的原因。


第三章
3-1 解:
(1)
(2)
(3)补零后:不变;变化,变的更加逼近(4)不能
3-2 解:
(1)令循环卷积
其余
(2)
其余
其余
(3)
其余
(4)补一个零后的循环卷积
其余
3-3 解:
,即可分辨出两个频率分量
本题中的两个频率分量不能分辨
3-4解:
对它取共轭:
与比较,
可知:1,只须将的DFT变换求共轭变换得;
2,将直接fft程序的输入信号值,得到;
3,最后再对输出结果取一次共轭变换,并乘以常数,即可求出IFFT变换的的值。
3-5解:可以;
证明:设
其中是在单位圆上的Z 变换,与
的关系如下:
是在频域上的N点的采样,与的关系如下:
相当于是在单位圆上的Z变换的N点采样。
3-6解:
,
,
图见电子版
3-7解:
,
,
,
,图见电子版
3-8解:
,,,同理:
图见电子版
3-9 解:
系统为单位脉冲响应
设加矩形窗后得到的信号为,
对应的短时离散频谱:
,
,
,
,
电子图
3-10 解:
(1)考虑对称位置取(2)考虑对称位置取(3)考虑对称位置取
3-11 解:
(1)
(2)
(3)
(4)
3-12
镜像为
镜像为
镜像为
镜像为
3-13 解:
(1)离散信号值:
(2)
3-14 解:
至少需要2000点个信号值
3-15解:
,,,。

第一章 离散时间信号与系统2.任意序列x(n)与δ(n)线性卷积都等于序列本身x(n),与δ(n-n 0)卷积x(n- n 0),所以(1)结果为h(n) (3)结果h(n-2) (2(4)3 .已知 10,)1()(<<--=-a n u a n h n,通过直接计算卷积和的办法,试确定单位抽样响应为 )(n h 的线性移不变系统的阶跃响应。
4. 判断下列每个序列是否是周期性的,若是周期性的,试确定其周期:)6()( )( )n 313si n()( )()873cos()( )(ππππ-==-=n j e n x c A n x b n A n x a分析:序列为)cos()(0ψω+=n A n x 或)sin()(0ψω+=n A n x 时,不一定是周期序列,nmm m n n y n - - -∞ = - ⋅ = = ≥ ∑ 2 31 2 5 . 0 ) ( 01当 3 4n m nm m n n y n 2 2 5 . 0 ) ( 1⋅ = = - ≤ ∑ -∞ = - 当 aa a n y n a a an y n n h n x n y a n u a n h n u n x m m nnm mn -==->-==-≤=<<--==∑∑--∞=---∞=--1)(11)(1)(*)()(10,)1()()()(:1时当时当解①当=0/2ωπ整数,则周期为0/2ωπ;②;为为互素的整数)则周期、(有理数当 , 2 0Q Q P QP =ωπ ③当=0/2ωπ无理数 ,则)(n x 不是周期序列。
解:(1)0142/3πω=,周期为14 (2)062/13πω=,周期为6 (2)02/12πωπ=,不是周期的 7.(1)[][]12121212()()()()()()[()()]()()()()[()][()]T x n g n x n T ax n bx n g n ax n bx n g n ax n g n bx n aT x n bT x n =+=+=⨯+⨯=+所以是线性的T[x(n-m)]=g(n)x(n-m) y(n-m)=g(n-m)x(n-m) 两者不相等,所以是移变的y(n)=g(n)x(n) y 和x 括号内相等,所以是因果的。

数字信号处理Digital signal processing物联网工程复变函数、线性代数、信号与系统2484816《数字信号处理》是物联网工程专业基础必修课。
主要研究如何分析和处理离散时间信号的基本理论和方法,主要培养学生在面对复杂工程问题时的分析、综合与优化能力,是一门既有系统理论又有较强实践性的专业基础课。
课程的目的在于使学生能正确理解和掌握本课程所涉及的信号处理的基本概念、基本理论和基本分析方法,来解决物联网系统中的信号分析问题。
培养学生探索未知、追求真理、勇攀科学高峰的责任感和使命感。
助力学生树立正确的价值观,培养思辨能力、工程思维和科学精神。
培养学生精益求精的大国工匠精神,激发学生科技报国的家国情怀和使命担当。
它既是学习相关专业课程设计及毕业设计必不可少的基础,同时也是毕业后做技术工作的基础。
运用时间离散系统的基本原理、离散时间傅里叶变换、 Z 变换、离散傅里叶变换(DFT)、快速傅里叶变换(FFT)、时域采样定理和频域采样定理等工程基础知识,分析物联网领域的复杂工程问题。
培养探索未知、追求真理、勇攀科学高峰的责任感和使命感。
助力学生树立正确的价值观,培养思辨能力、工程思维和科学精神。
说明利用DFT 对摹拟信号进行谱分析的过程和误差分析、区分各类网络的结构特点;借助文献研究运用窗函数法设计具有线性相位的FIR 数字滤波器,分析物联网领域复杂工程问题解决过程中的影响因素,从而获得有效结论的能力。
培养学生精益求精的大国工匠精神,激发学生科技报国的家国情怀和使命担当。
第一章 时域离散信号与系统(1)时域离散信号表示; (2)时域离散系统;(3)时域离散系统的输入输出描述法; * (4)摹拟信号数字处理方法;:数字信号处理中的基本运算方法,时域离散系统的线性、时不变性及系统的因果性和稳定性。
时域采样定理。
培养探索未知、 追求真理、 勇攀科学高峰的责任感和使命感。
:时域离散系统的线性、时不变性及系统的因果性和稳定性、时域采样定理。

数字信号处理刘顺兰第三章完整版习题解答一、题目解答1. 题目利用时域抽样、频域抽样、零填充、插值法等,实现信号的变换。
1.1 时域抽样时域抽样是指将一个连续时间信号在时间轴上的等间隔位置上进行采样,可以得到一个离散时间信号。
时域抽样的原理是,将时间轴上的信号按照一定的时间间隔进行采样,每个采样点的振幅值就是该点对应的连续时间信号的振幅值。
时域抽样可以通过以下步骤进行实现:1.假设连续时间信号为x(t),采样频率为Fs(采样频率是指每秒采样的次数),采样间隔为Ts(采样间隔是指相邻两个采样点之间的时间间隔)。
2.根据采样频率和采样间隔,计算出采样点数N:N =Fs * T,其中T为采样时长。
为Ts。
4.在每段的中点位置进行采样,得到N个采样点。
5.将N个采样点按照时域顺序排列,即可得到离散时间信号。
1.2 频域抽样频域抽样是指将一个连续频谱信号在频率轴上的等间隔位置上进行采样,可以得到一个离散频谱信号。
频域抽样的原理是,将频率轴上的信号按照一定的频率间隔进行采样,每个采样频率点上的能量值就是该频率点对应的连续频谱信号的能量值。
频域抽样可以通过以下步骤进行实现:1.假设连续频谱信号为X(f),采样频率为Fs(采样频率是指每秒采样的次数),采样间隔为Δf(采样间隔是指相邻两个采样频率点之间的频率间隔)。
2.根据采样频率和采样间隔,计算出采样点数N:N =Fs / Δf,其中Δf为采样频率点之间的频率间隔。
为Δf。
4.在每段的中点位置进行采样,得到N个采样频率点。
5.将N个采样频率点按照频域顺序排列,即可得到离散频谱信号。
1.3 零填充零填充是指在信号的末尾添加一些零值样本,使得信号的长度变长。
零填充的原理是,通过增加信号的长度,可以在时域和频域上提高信号的分辨率,从而更精确地观察信号的特征。
零填充可以通过以下步骤进行实现:1.假设原始信号为x(n),长度为N。
2.计算需要填充的长度L,L > 0。
数字信号处理课后答案 高西全、丁美玉版1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它〔1〕画出()x n 序列的波形,标上各序列的值;〔2〕试用延迟单位脉冲序列及其加权和表示()x n 序列; 〔3〕令1()2(2)x n x n =-,试画出1()x n 波形; 〔4〕令2()2(2)x n x n =+,试画出2()x n 波形; 〔5〕令3()2(2)x n x n =-,试画出3()x n 波形。
解:〔1〕x(n)的波形如题2解图〔一〕所示。
〔2〕()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-〔3〕1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图〔二〕所示。
〔4〕2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图〔三〕所示。
〔5〕画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图〔四〕所示。
3. 判断下面的序列是否是周期的,假设是周期的,确定其周期。
〔1〕3()cos()78x n A n ππ=-,A 是常数;〔2〕1()8()j n x n e π-=。
解:〔1〕3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; 〔2〕12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理教案第一章:数字信号处理概述1.1 数字信号处理的概念介绍数字信号处理的定义和特点解释信号的分类和数字信号的优势1.2 数字信号处理的发展历程回顾数字信号处理的发展历程和重要里程碑介绍数字信号处理的重要人物和贡献1.3 数字信号处理的应用领域概述数字信号处理在通信、音频、图像等领域的应用举例说明数字信号处理在实际应用中的重要性第二章:离散时间信号处理基础2.1 离散时间信号的概念介绍离散时间信号的定义和特点解释离散时间信号与连续时间信号的关系2.2 离散时间信号的运算介绍离散时间信号的基本运算包括翻转、平移、求和等给出离散时间信号运算的示例和应用2.3 离散时间系统的特性介绍离散时间系统的概念和特性解释离散时间系统的因果性和稳定性第三章:数字滤波器的基本概念3.1 数字滤波器的定义和作用介绍数字滤波器的定义和其在信号处理中的作用解释数字滤波器与模拟滤波器的区别3.2 数字滤波器的类型介绍不同类型的数字滤波器包括FIR、IIR、IIR 转换滤波器等分析各种类型数字滤波器的特点和应用场景3.3 数字滤波器的设计方法介绍数字滤波器的设计方法包括窗函数法、插值法等给出数字滤波器设计的示例和步骤第四章:离散傅里叶变换(DFT)4.1 离散傅里叶变换的定义和原理介绍离散傅里叶变换的定义和原理解释离散傅里叶变换与连续傅里叶变换的关系4.2 离散傅里叶变换的性质介绍离散傅里叶变换的性质包括周期性、对称性等给出离散傅里叶变换性质的证明和示例4.3 离散傅里叶变换的应用概述离散傅里叶变换在信号处理中的应用包括频谱分析、信号合成等举例说明离散傅里叶变换在实际应用中的重要性第五章:快速傅里叶变换(FFT)5.1 快速傅里叶变换的定义和原理介绍快速傅里叶变换的定义和原理解释快速傅里叶变换与离散傅里叶变换的关系5.2 快速傅里叶变换的算法介绍快速傅里叶变换的常用算法包括蝶形算法、Cooley-Tukey算法等给出快速傅里叶变换算法的示例和实现步骤5.3 快速傅里叶变换的应用概述快速傅里叶变换在信号处理中的应用包括频谱分析、信号合成等举例说明快速傅里叶变换在实际应用中的重要性第六章:数字信号处理中的采样与恢复6.1 采样定理介绍采样定理的定义和重要性解释采样定理在信号处理中的应用6.2 信号的采样与恢复介绍信号采样与恢复的基本概念解释理想采样器和实际采样器的工作原理6.3 信号的重建与插值介绍信号重建和插值的方法解释插值算法的原理和应用第七章:数字信号处理中的离散余弦变换(DCT)7.1 离散余弦变换的定义和原理介绍离散余弦变换的定义和原理解释离散余弦变换与离散傅里叶变换的关系7.2 离散余弦变换的应用概述离散余弦变换在信号处理中的应用包括图像压缩、信号分析等举例说明离散余弦变换在实际应用中的重要性7.3 离散余弦变换的快速算法介绍离散余弦变换的快速算法包括8x8 DCT算法等给出离散余弦变换快速算法的示例和实现步骤第八章:数字信号处理中的小波变换8.1 小波变换的定义和原理介绍小波变换的定义和原理解释小波变换与离散傅里叶变换的关系8.2 小波变换的应用概述小波变换在信号处理中的应用包括图像去噪、信号分析等举例说明小波变换在实际应用中的重要性8.3 小波变换的快速算法介绍小波变换的快速算法包括Mallat算法等给出小波变换快速算法的示例和实现步骤第九章:数字信号处理中的自适应滤波器9.1 自适应滤波器的定义和原理介绍自适应滤波器的定义和原理解释自适应滤波器在信号处理中的应用9.2 自适应滤波器的设计方法介绍自适应滤波器的设计方法包括最小均方误差法等给出自适应滤波器设计的示例和步骤9.3 自适应滤波器的应用概述自适应滤波器在信号处理中的应用包括噪声抑制、信号分离等举例说明自适应滤波器在实际应用中的重要性第十章:数字信号处理的综合应用10.1 数字信号处理在通信系统中的应用介绍数字信号处理在通信系统中的应用包括调制解调、信道编码等分析数字信号处理在通信系统中的重要性10.2 数字信号处理在音频处理中的应用介绍数字信号处理在音频处理中的应用包括声音合成、音频压缩等分析数字信号处理在音频处理中的重要性10.3 数字信号处理在图像处理中的应用介绍数字信号处理在图像处理中的应用包括图像滤波、图像增强等分析数字信号处理在图像处理中的重要性10.4 数字信号处理在其他领域的应用概述数字信号处理在其他领域的应用包括生物医学信号处理、地震信号处理等分析数字信号处理在其他领域中的重要性重点和难点解析重点环节1:数字信号处理的概念和特点数字信号处理是对模拟信号进行数字化的处理和分析数字信号处理具有可重复性、精确度高、易于存储和传输等特点需要关注数字信号处理与模拟信号处理的区别和优势重点环节2:数字信号处理的发展历程和应用领域数字信号处理经历了从早期研究到现代应用的发展过程数字信号处理在通信、音频、图像等领域有广泛的应用需要关注数字信号处理的重要人物和里程碑事件重点环节3:离散时间信号处理基础离散时间信号是数字信号处理的基础需要关注离散时间信号的定义、特点和运算方法理解离散时间信号与连续时间信号的关系重点环节4:数字滤波器的基本概念和类型数字滤波器是数字信号处理的核心组件需要关注数字滤波器的定义、类型和设计方法理解不同类型数字滤波器的特点和应用场景重点环节5:离散傅里叶变换(DFT)离散傅里叶变换是数字信号处理中的重要工具需要关注离散傅里叶变换的定义、性质和应用理解离散傅里叶变换与连续傅里叶变换的关系重点环节6:快速傅里叶变换(FFT)快速傅里叶变换是离散傅里叶变换的优化算法需要关注快速傅里叶变换的定义、算法和应用理解快速傅里叶变换与离散傅里叶变换的关系重点环节7:数字信号处理中的采样与恢复采样与恢复是数字信号处理的关键环节需要关注采样定理的重要性、信号的采样与恢复方法理解插值算法的原理和应用重点环节8:数字信号处理中的离散余弦变换(DCT)离散余弦变换是数字信号处理中的另一种重要变换需要关注离散余弦变换的定义、应用和快速算法理解离散余弦变换与离散傅里叶变换的关系重点环节9:数字信号处理中的小波变换小波变换是数字信号处理的另一种重要变换需要关注小波变换的定义、应用和快速算法理解小波变换与离散傅里叶变换的关系重点环节10:数字信号处理中的自适应滤波器自适应滤波器是数字信号处理中的高级应用需要关注自适应滤波器的定义、设计方法和应用领域理解自适应滤波器在信号处理中的重要性本教案涵盖了数字信号处理的基本概念、发展历程、离散时间信号处理、数字滤波器、离散傅里叶变换、快速傅里叶变换、采样与恢复、离散余弦变换、小波变换、自适应滤波器等多个重点环节。
第一章 离散时间信号与系统2.任意序列x(n)与δ(n)线性卷积都等于序列本身x(n),与δ(n-n 0)卷积x(n- n 0),所以(1)结果为h(n) (3)结果h(n-2) (2x(m)()h n m -n1 1 1 0 0 0 0 y(n) 0 11 1 1 12 2 1 1 13 3 1 1 1 1 34 0 1 1 1 1 2 511111(4)3 .已知 10,)1()(<<--=-a n u a n h n,通过直接计算卷积和的办法,试确定单位抽样响应为 )(n h 的线性移不变系统的阶跃响应。
4. 判断下列每个序列是否是周期性的,若是周期性的,试确定其周期:)6()( )( )n 313si n()( )()873cos()( )(ππππ-==-=n j e n x c A n x b n A n x a分析:序列为)cos()(0ψω+=n A n x 或)sin()(0ψω+=n A n x 时,不一定是周期序列, nmm m n n y n - - -∞ = - ⋅ = = ≥ ∑ 2 31 2 5 . 0 ) ( 01当 3 4n m nm m n n y n 2 2 5 . 0 ) ( 1⋅ = = - ≤ ∑ -∞ = - 当 aa a n y n a a an y n n h n x n y a n u a n h n u n x m m nnm mn -==->-==-≤=<<--==∑∑--∞=---∞=--1)(11)(1)(*)()(10,)1()()()(:1时当时当解①当=0/2ωπ整数,则周期为0/2ωπ;②;为为互素的整数)则周期、(有理数当 , 2 0Q Q P QP =ωπ ③当=0/2ωπ无理数 ,则)(n x 不是周期序列。
解:(1)0142/3πω=,周期为14 (2)062/13πω=,周期为6 (2)02/12πωπ=,不是周期的 7.(1)[][]12121212()()()()()()[()()]()()()()[()][()]T x n g n x n T ax n bx n g n ax n bx n g n ax n g n bx n aT x n bT x n =+=+=⨯+⨯=+所以是线性的T[x(n-m)]=g(n)x(n-m) y(n-m)=g(n-m)x(n-m) 两者不相等,所以是移变的y(n)=g(n)x(n) y 和x 括号内相等,所以是因果的。