下载文档原格式
第5章静定平面桁架复习思考题1．桁架的计算简图作了哪些假设？它与实际的桁架有哪些差别？答：（1）桁架的计算简图假设①各结点都是无摩擦的理想铰；②各杆轴都是直线，并在同一平面内且通过铰的中心；③荷载只作用在结点上并在桁架的平面内。
（2）桁架的计算简图与实际桁架的差别①结点的刚性。
②各杆轴线不可能绝对平直，在结点处也不可能准确交于一点。
③非结点荷载（例如杆件自重、风荷载等）。
④结构的空间作用，等等。
2．如何根据桁架的几何构造特点来选择计算顺序？答：根据桁架的几何构造特点来选择计算顺序的方法（1）找出零杆根据节点的几何特征和外部受力特点判断出零杆。
（2）选择合适的方法求解桁架①用节点法解简单桁架时，在求出支座反力后，可按与几何组成相反的顺序，从最后的结点开始，依次倒算回去，便能顺利地用结点法求出所有杆件的内力。
②求解联合桁架时，用结点法将会遇到未知力超过两个的结点，可以先用截面法将联合杆件的内力求出，再用结点法求解其它杆件的内力。
③求解复杂桁架时，根据桁架的几何构造特点看，可先算出截面单杆的内力，再选择合适的计算方法求解剩余杆的内力。
3．在结点法和截面法中，怎样尽量避免解联立方程？答：在结点法和截面法中，尽量避免解联立方程的方法：（1）采用结点法时，为避免解联立方程，可改选投影轴方向或者改用力矩平衡方程（向力的汇交点取矩）。
（2）采用截面法时，使用力矩法的关键在于选取合理的力矩中心，因此应尽量选取多力汇交点作为力矩中心；使用投影法的过程中，应尽量选择多个力所在方向作为力分解的坐标轴。
4．零杆既然不受力，为何在实际结构中不把它去掉？答：在实际结构中不把零杆去掉的原因：（1）在实际结构中，工况更复杂，荷载不是一成不变的，荷载改变后，“零杆”可能变为非零杆。
因此，为了保证结构的几何形状在任何载荷作用下都不会改变，零杆不能从桁架中除去。
（2）在理想桁架（做了诸多假设）中“零杆”才是零杆，而实际结构中，零杆的内力也不是零，只是较小而已。
《结构力学》第五章静定平面桁架《结构力学》第五章讲述了静定平面桁架的内容。
静定平面桁架是指在平面内所有节点的约束力和外力之间可以通过力平衡方程求解出来的桁架结构。
本章内容主要包括静定平面桁架的基本概念和原理，以及常见的静定平面桁架的求解方法。
在静定平面桁架中，基本概念和原理非常重要。
首先，了解节点的约束力和外力之间的平衡关系非常重要。
通过平衡方程可以解决约束力和外力之间的关系。
其次，了解节点的自由度也是关键，自由度指节点上的约束力的个数。
在静态平面桁架中，节点的自由度为2，因为节点上只有两个方向的约束力。
然后，了解节点的外部力和内部力之间的关系也是很关键的，通过平衡方程可以解决这些关系。
此外，了解支撑条件、桁架的刚度和材料的性质也是非常重要的。
为了求解静定平面桁架，可以使用力法、位移法或者变形能法。
力法是最常用的一种求解方法，其基本思想是通过平衡条件和节点自由度来解决节点的约束力和外力之间的关系。
具体来说，可以先通过平衡方程得到节点处的约束力之和，然后通过平衡方程再次求解每个节点的约束力。
位移法是通过求解位移来求解约束力和外力之间的关系。
其基本思想是通过平衡方程求解节点的约束力和位移之间的关系，然后通过位移和刚度来求解节点的约束力。
位移法的求解过程比较繁琐，但是可以在复杂情况下准确求解静定平面桁架。
变形能法是一种通过统计力学和能量原理来求解约束力和外力之间的关系的方法。
通过求解系统的总能量和变形能量的变化，可以求解节点的约束力。
变形能法的求解过程相对简单，但是需要对系统的能量进行合理的选择。
在应用静定平面桁架时，需要考虑一些实际问题。
首先，需要考虑桁架的几何形状和荷载情况。
几何形状和荷载情况对桁架的受力和变形有很大影响，因此需要对这些进行准确的描述和分析。
其次，需要考虑桁架的材料性质和刚度。
不同材料和刚度会对桁架的受力和变形产生不同影响。
最后，需要注意桁架的稳定性和安全性。
在设计和使用桁架时，需要遵循一些安全性要求，以确保桁架的结构稳定和使用安全。
第2章 平面体系的机动分析2.1 复习笔记【知识框架】【重点难点归纳】一、体系1．几何不变体系几何不变体系是指在任意载荷作用时，若不考虑材料的变形，则其几何形状与位置均能 几何不变体系 平面体系的概述 常变体系几何可变体系 瞬变体系自由度 自由度定义自由度个数平面体系的计算自由度 联系的定义联系 联系的分类：链杆、单铰、复铰多余联系 一般体系 计算自由度 计算自由度的公式 铰结链杆体系 自由度与体系是否几何不变的关系 三刚片规则 几何不变体系的基本组成规则 二元体规则两刚片规则 瞬变体系 瞬变体系的定义 三刚片规则中，三个铰在同一直线上的体系 瞬变体系 几种常见的瞬变体系 二元体的两杆共线的体系两刚片规则中，三根链杆交于同一点，且互不平行两刚片规则中，三根链杆全平行无穷远点的性质三刚片体系中虚铰在无穷远处的情况 一铰无穷远两铰无穷远三铰无穷远几何构造与静定性的关系 静定体系：体系几何不变且无多余联系超静定体系：体系几何不变，而且有多余联系 平面体系的机动分析保持不变的体系。
2．几何可变体系（1）定义几何可变体系是指在很小的荷载作用下，即使不考虑材料的变形，会发生机械运动而不能保持原有的几何形状或位置的体系。
（2）分类①常变体系；②瞬变体系。
二、平面体系的计算自由度1．自由度（1）自由度定义自由度是指体系运动时所具有的独立运动方式数目，也就是体系运动时可以独立变化的几何参数数目，或者说确定体系位置所需的独立坐标数目。
（2）自由度个数①平面内的一个点的自由度为2；②平面内的一个刚体的自由度为3；③机械中常用的机构是沿特定的一种轨迹运动，具有一个自由度；④几何不变体系不能发生任何运动，其自由度应等于零；⑤凡自由度大于零的体系都是几何可变体系。
2．联系（1）联系的定义联系是指限制运动的装置，也称为约束。
一个联系是指能减少一个自由度的装置。
（2）联系的分类①链杆一根链杆为一个联系。
②铰a．单铰单铰是指联结两个刚片的一个铰。
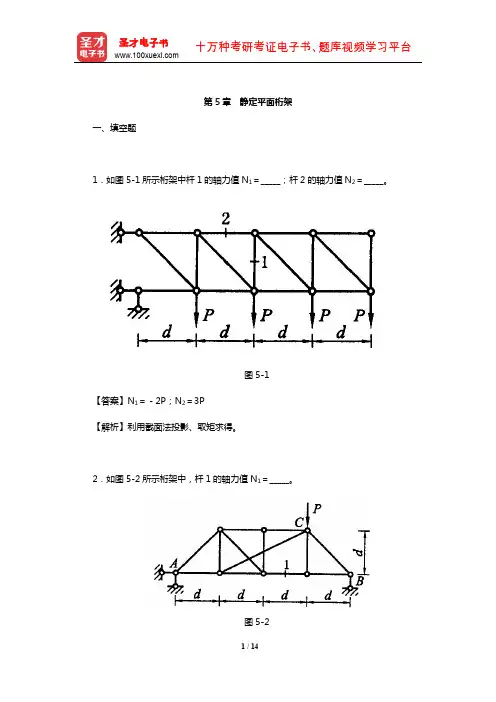
第5章静定平面桁架一、填空题1．如图5-1所示桁架中杆1的轴力值N1＝_____；杆2的轴力值N2＝_____。
图5-1【答案】N1＝－2P；N2＝3P【解析】利用截面法投影、取矩求得。
2．如图5-2所示桁架中，杆1的轴力值N1＝_____。
图5-2【答案】【解析】先以A点取矩求得B处支座反力，再利用截面法取矩求杆1轴力。
3．如图5-3所示结构中，杆1的轴力值N1＝_____；杆2的轴力值N2＝_____。
图5-3【答案】N1＝P；N2＝－2P【解析】取上半部分分析，对右上角的结点取矩得出N2，再求出支座反力即可求出N1。
二、判断题1．如图5-4所示桁架中杆1的轴力为1kN。
（）图5-4【答案】对【解析】用截面法、取矩。
2．如图5-5所示桁架中杆1的轴力为零。
（）图5-5【答案】对【解析】左右支座竖向反力均为向上的P，用截面法，由∑Y＝0即可得出。
3．如图5-6所示桁架中杆1的轴力为P。
（）图5-6 【答案】错【解析】反对称荷载，对称杆轴为零。
4．如图5-7所示桁架中杆1的轴力为2P。
（）图5-7 【答案】错【解析】截面法，三、选择题1．如图5-8所示桁架中零杆（含零支杆）个数为（）。
A．0根B．1根C．2根D．3根图5-8【答案】D【解析】利用对称性可知，水平支杆和内部的两根杆为零杆。
2．如图5-9所示桁架中杆1的轴力值N1为（）。
A．－pB．－2pC．D．－1.414p图5-9【答案】C【解析】先结点A后结点B，两次用结点法可求得。
3．如图5-10所示结构中杆1的轴力值N0为（）。
A．0B．1.414PC．－1.414PD．0.707P图5-10。
第1章绪论复习思考题1．结构力学的研究对象和具体任务是什么？答：（1）结构力学的研究对象结构力学研究的主要对象是杆系结构。
（2）结构力学的具体任务①研究结构在荷载等因素作用下的内力和位移的计算。
在此基础上，即可利用后续相关专业课程知识进行结构设计或结构验算；②研究结构的稳定计算，以及动力荷载作用下结构的动力反应；③研究结构的组成规则和合理形式等问题。
2．什么是荷载？结构主要承受哪些荷载？如何区分静力荷载和动力荷载？答：（1）荷载的定义荷载是指作用在结构上的主动力。
（2）荷载的分类①按作用时间分为：恒载和活载。
②按荷载的作用位置是否变化分为：固定荷载和移动荷载。
③按荷载对结构所产生的动力效应大小分为：静力荷载和动力荷载。
（3）静力荷载和动力荷载的主要区别荷载是否使结构产生不可忽略的加速度，即是否可以略去惯性力的影响。
若可忽略加速度（惯性力），则为静荷载；若不可忽略加速度（惯性力），则为动荷载。
3．什么是结构的计算简图？如何确定结构的计算简图？答：（1）计算简图的定义结构的计算简图是指略去次要因素，用一个简化图形来代替实际结构的图形。
（2）确定计算简图的方法①杆件的简化，常以其轴线代表。
②支座和结点的简化。
③荷载的简化，常简化为集中荷载及线分布荷载。
④体系的简化，将空间结构简化为平面结构。
4．结构的计算简图中有哪些常用的支座和结点？答：结构的计算简图中常用的支座和结点分别有：（1）常用的支座：活动铰支座、固定铰支座、固定支座、滑动支座。
（2）常用的结点：铰结点、刚结点、组合结点。
5．哪些结构属于杆系结构？它们有哪些受力特征？答：（1）杆系结构的定义杆系结构是指长度远大于其他两个尺度（即截面的高度和宽度）的杆件组成的结构。
杆系结构包括：梁、拱、刚架、桁架、组合结构、悬索结构。
（2）各种杆系结构的受力特征①梁。
梁是一种受弯杆件，其轴线通常为直线，当荷载垂直于梁轴线时，横截面上的内力只有弯矩和剪力，没有轴力。
5.1 复习笔记【知识框架】
【重点难点归纳】
一、桁架的基本概念（表5-1-1） ★★
二、结点法（见表5-1-2） ★★★★★
表5-1-2 结点法
图5-1-1
三、截面法（表5-1-3） ★★★★★
表5-1-3 截面法
四、常用三种梁式桁架的比较（见表5-1-4） ★★
表5-1-4 常用三种梁式桁架的比较
图5-1-2
五、用零载法分析体系的几何构造（见表5-1-5） ★★
表5-1-5 零载法
5.2 课后习题详解
复习思考题
1．桁架的计算简图作了哪些假设？它与实际的桁架有哪些差别？
答：（1）桁架的计算简图假设
①各结点都是无摩擦的理想铰，也即是铰结点只传递集中力，不传递弯矩；
②各杆轴均为直线，并在同一平面内且通过铰的中心；
③荷载只作用在结点上并在桁架的平面内，即忽略风荷载、自重等杆上作用。
（2）桁架的计算简图与实际桁架的差别
①结点的刚性，即不存在绝对光滑的铰结点。
②各杆轴线为理想直线，实际结点不可能准确交于一点。
③非结点荷载（例如杆件自重、风荷载等）。
④结构的空间作用，等等。
