当前位置：文档之家 › 5.1回溯法的算法框架

5.1回溯法的算法框架

  • 格式：ppt
  • 大小：690.50 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

回溯算法

回溯算法

回溯算法回溯算法是程序设计中最重要的基础算法之一，也是搜索算法中的一种控制策略，回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，选择另外一条路再走。

它是从初始状态出发，运用题目给出的条件、规则，按照深度优先搜索的顺序扩展所有可能情况，从中找出满足题意要求的解答。

回溯法是求解特殊型计数题或较复杂的枚举题中使用频率最高的一种算法。

一、回溯算法说明1.算法定义回溯算法是搜索算法中的一种控制策略。

它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。

算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解，如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。

否则进入该子树，继续按深度优先的策略进行搜索。

回溯算法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。

回溯算法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束。

这种以深度优先的方式系统地搜索问题的解的算法称为回溯算法。

2.算法描述回溯算法描述如下：procedure run（当前状态）；vari：integer；beginif当前状态为边界then beginif 当前状态为最佳目标状态then记下最优结果；exit；{回溯}end；{then}for i←算符最小值to 算符最大值dobegin算符i作用于当前状态，扩展出一个子状态；if (子状态满足约束条件) and (子状态满足最优性要求)then run(子状态)；end；{for}end；{run}二、经典例题分析[问题描述]八皇后问题是一个古老而著名的问题，是回溯算法的典型例题。

该问题由19世纪著名的数学家高斯于1850年提出：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

高斯认为有76种方案。

第5章回溯法PPT课件

第5章回溯法PPT课件

二、回溯的一般描述
一旦某个j元组（x1，x2，…，xj）违反D中仅涉及 x1，x2，…，xj 的一个约束，就可以肯定，以（x1， x2，…，xj）为前缀的任何n元组
（x1，x2，…，xj，xj+1，…，xn）都不会是问题P 的解。
三、回溯的一般步骤
回溯法正是针对这类问题，利用这类问题的 上述性质而提出来的比枚举法效率更高的算 法。
由于这是第一次用计算机证明数学定理，所以哈肯 和阿佩尔的工作，不仅是解决了一个难题，而且从 根本上拓展了人们对“证明”的理解，引发了数学 家从数学及哲学方面对“证明”的思考。
实例—n皇后问题
在一个n×n的棋盘上放置n个国际象棋中 的皇后，要求所有的皇后之间都不形成攻 击。请你给出所有可能的排布方案数。
n
4
5
6
7
8
总数
2
10
4
40
92
n皇后问题
对于n皇后问题而言，我们很难找出很合适的方法 来快速的得到解，因此，我们只能采取最基本的枚 举法来求解。
但我们知道，在n×n的棋盘上放置n个棋子的所有
回溯算法（一）
什么是回溯
入口回溯
▪迷宫游戏
回溯
➢什么是回溯法
回溯
▪回溯法是一个既带
有系统性又带有跳跃
性的的搜索算法
回溯
▪回溯法是以深度优先的方式系统地搜索问题 出口 的解, 它适用于解一些组合数较大的问题。
回溯(Trackback)是什么？
为什么回溯？
怎样回溯？
What
Why
How
一、回溯的概念
解问题P的最朴素的方法就是枚举法，即对E 中的所有n元组逐一地检测其是否满足D的全 部约束，显然，其计算量是相当大的。

第五章 回溯算法

第五章 回溯算法

的结点
» 扩展结点:正在产生儿子的结点
» 死结点:所有儿子已经全部产生的结点
活结点
扩展结点
死结点
4
» 采用深度优先法生成解空间树：如果对一
个扩展结点R，一旦产生了一个儿子 C，就 将 C 当做新的扩展结点。在完成对子树 C 的穷尽搜索后，将 R 再次变成扩展结点， 继续生成 R 的下一个儿子。
扩展结点
这3个作业的6种可能的调度方 案是1,2,3；1,3,2；2,1,3； 2,3,1；3,1,2；3,2,1；对应 的完成时间和分别是19，18， 20，21，19，19。最佳调度方 案是1,3,2。
f=3+7+8=18
M1 M2 f=4+6+10=20
26
void backtrack (int t) { if (t>n) output(x); else for (int i=t;i<=n;i++) { swap(x[t], x[i]); if (legal(t)) backtrack(t+1); swap(x[t], x[i]); } }
27
void backtrack (int t) { if (t>n) output(x);
else
for (int i=t;i<=n;i++) { swap(x[t], x[i]); if (legal(t)) backtrack(t+1); swap(x[t], x[i]); } }
void backtrack(int i) { if (i > n) { for (int j = 1; j <= n; j++) bestx[j] = x[j]; bestf = f; } else for (int j = i; j <= n; j++) { f1+=m[x[j]][1]; f2[i]=((f2[i-1]>f1)?f2[i-1]:f1)+m[x[j]][2]; f+=f2[i]; if (f < bestf) { swap(x,i,j); backtrack(i+1); swap(x,i,j); } f1-=m[x[j]][1]; f-=f2[i]; } }

回溯法

回溯法

西安邮电大学计算机学院
第5章 回溯法
以示例图为例，当 n = 4 时，假定驻地为节点 1，则旅行售货员问题的解空间是：
{ ( 1，2，3，4，1 )、 ( 1，2，4，3，1 )、 ( 1，3，2，4，1 )、 ( 1，3，4，2，1 )、 ( 1，4，2，3，1 )、 ( 1，4，3，2，1 ) }，共有（4 - 1）！= 3！= 6 种可能。 当节点数为 n 时，有 （n - 1）！种可能的解（这是一个排列问题）。
计算机科学的先驱、英国科学家阿兰· 麦席森· 图灵
第5章 回溯法
回溯法以深度优先的方式搜索解空间。如果回溯法在执行过程
中判断解空间树的某个节点不包含问题的解时，则跳过对以 该节点为根的子树的搜索（子树中一定不会包含问题的解）， 逐层向其祖先节点回溯；否则进入该子树，继续按深度优先策 略搜索。这也是“回溯法”名称的由来。
西安邮电大学计算机学院
第5章 回溯法
5.1.4 迭代回溯
采用树的非递归深度优先遍历算法，可将回溯法表示为一个非递归迭代过程。 void IterativeBacktrack( ) { int t = 1; while ( t > 0 ) { if ( f( n, t ) <= g( n, t ) ) for ( int i = f( n, t ); i <= g( n, t ); i++ ) { x[ t ] = h( i ); if ( Constraint( t ) && Bound( t ) ) { if ( Solution( t ) ) output( x ); else t++; } } else t--; } 回溯法
（2）解空间结构 定义了问题的解空间后，还应将解空间很好地组织起来，使得能用回溯法方便地 搜索整个解空间。通常将解空间组织成树或图的形式。如果将解空间组织成树的

回溯算法框架

回溯算法框架

回溯算法框架回溯算法就是将每⼀种可能遍历⼀遍，⽽且每⼀种结果都不相同解决⼀个回溯问题，实际上就是解决⼀个决策树的遍历过程我们需要思考三个问题：路径：已经做出的选择，将来要存储到结果的路径选择列表：当前可以做的选择结束条件：就是遍历到达末尾时候的条件解决回溯算法有⼀个框架：LinkedList<LinkedList<元素类型>> 结果集 = new LinkedList<>();private void backtrack(路径, 选择列表) {for (元素类型 o : 选择列表) {if (到达末尾) {将选择列表添加到结果集中;}做选择;backtrack(路劲, 选择列表);撤销选择;}}回溯算法的最核⼼的框架就是这段伪代码了，在循环中进⾏递归，在递归前做选择，在递归结束后撤销选择，到达末尾就将所做的选择添加到结果集中利⽤回溯，可以实现全排列问题：import java.util.LinkedList;public class Test {private static LinkedList<LinkedList<Integer>> res = new LinkedList<>();public static void main(String[] args) {int[] nums = {1, 2, 3, 4, 5, 6, 7, 8};LinkedList<LinkedList<Integer>> list = permutation(nums);System.out.println(list.size());}private static LinkedList<LinkedList<Integer>> permutation(int[] nums) {LinkedList<Integer> track = new LinkedList<>();backtrack(nums, track);return res;}private static void backtrack(int[] nums, LinkedList<Integer> track) {// 如果到达了末尾就将结果添加到res链表中if (nums.length == track.size()) {res.add(new LinkedList<>(track));return;}for (int i : nums) {//如果遍历过了就跳过if (track.contains(i)) {continue;}track.add(i);backtrack(nums, track);track.removeLast();}}}。

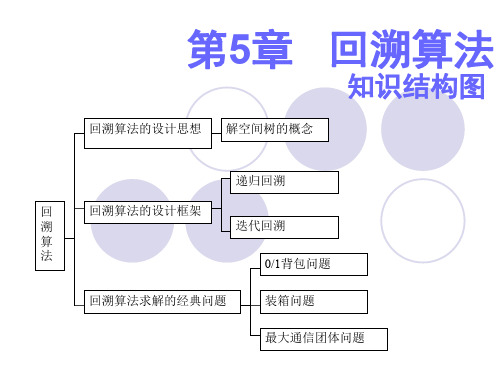
第5章 回溯算法

第5章 回溯算法

第5章 回溯算法
当我们确定了解空间的组织结构以后，回溯算法便可以 从起始结点（根结点）出发，以深度优先方式搜索整个 解空间。于是，这个起始结点既成为活结点，同时又成 为当前的扩展结点。在当前的扩展结点处，搜索过程就 向着纵深方向移动到一个新的结点，而这个新的结点就 成为当前的一个新的活结点，并且成为当前的扩展结点。 如果在当前的扩展结点处不能再向纵深方向移动，那么 当前的这个扩展结点就成为死结点。此时，就不能继续 纵深下去，应立即往回移动（这就是回溯）到最近的一 个活结点处，并且使得这个活结点成为当前的扩展结点。 回溯算法就是以这种方式递归地在解空间中进行不断地 搜索活动，直到找出所需要的解或者解空间中已经不再 有活结点时为止。
第5章 回溯算法
例如，当我们在求解0/1背包问题时，通常在使 用回溯算法的同时采用剪枝函数剪除导致不可行 解的子树。在使用回溯算法求解旅行商问题时， 如果从根结点到当前的扩展结点处的部分周游路 线的成本已经超过了当前找到的周游路线成本， 那么就可以判定以此结点为根结点的子树中不包 含最优解，因此，可以将该子树剪除。
溯
迭代回溯
算
法
0/1背包问题
回溯算法求解的经典问题
装箱问题
最大通信团体问题
第5章 回溯算法
回溯算法具有通用的解题算法之称。使用回溯算法可
以系统地搜索一个问题的全部解或者其中的任意一个解。 回溯算法是一个既具有系统性，同时又具有跳跃性的搜 索算法。它在问题的解空间树中，往往可以根据深度优 先策略，由根结点出发依次搜索整棵解空间树。当回溯 算法在搜索到解空间树中的任意一个结点时，应首先判 断该结点是否包含原问题的解。如果包含，就直接进入 到该子树，并且继续按照深度优先策略搜索问题的解； 如果不包含，那么就跳过对以此结点为根结点的子树的 搜索，并且依次逐层向其祖先结点回溯。当我们使用回 溯算法求一个问题的全部解时，通常要回溯到解空间树 的根结点，并且当根结点的所有子树都已经被搜索或者 遍历了一遍之后方能结束。然而，如果当只需要使用回 溯算法求问题的一个解时，通常只需要搜索到问题的一 个解就可以结束。这种以深度优先系统搜索问题的解的 算法称为回溯算法，它适用于求解数据规模比较大的问 题。

回溯法




限界函数：如果（x1,x2,…,xi）是到当前E结点 的路径，那么xi的儿子结点xi+1是一 些这样的结点，它们使得 （x1,x2,…,xi,xi+1）表示没有两个皇 后正在相互攻击的一种棋盘格局。 开始状态：根结点1，表示还没有放置任何皇后。 结点的生成：依次考察皇后1——皇后n的位置。
•发现超出边界，跳法失败。
•退回A 点试跳 法2，仍失败。
马
②
马
③ ①
•再退回A点试跳法3，成功，记录新 点坐标为A2 ，保存该步出发点A的 坐标及跳法编号， 以便回溯时使用。
►然后以A2点为起点，仍按重复上述办法试探下一
步，直到达到目标状态B为止，则找到一种跳动方 法。
7
A
右上1 A2 右上1 右下2 A3 右上1 右下2 右上1 B 右上2 右下2 右下1 A4 右上2 右下1 右下1 右上2 右上2 右下1 右下2
注意：同一个问题可以有多种表示，有些表示方法更 简单，所需表示的状态空间更小（存储量少，搜索方 法简单）。
11
回溯法解决问题的一般方法
► 回溯法的基本做法是搜索（求某一解），或是一
种组织得井井有条的，能避免不必要搜索的穷举 式搜索法（求所有解）。这种方法适用于解一些 组合数相当大的问题。 ► 为了更有效的进行搜索，将所有的解构造成树的 结构，在这个解空间树中，从根结点出发按深度 优先策略搜索整个解空间树。 ► 当算法搜索至解空间树的任意一点时，先判断该 结点是否包含问题的解。如果不包含，则跳过对 该结点为根的子树的搜索，向其结点回溯；否则， 进入该子树，继续按深度优先策略搜索。
R，一旦产生了它的一个儿子C，就把C当做新的扩 展结点。在完成对子树C（以C为根的子树）的穷尽 搜索之后，将R重新变成扩展结点，继续生成R的下 一个儿子（如果存在）

回溯法的三种框架

回溯法的三种框架
回溯法的三种框架分别是：
1.非递归回溯框架：对应的解空间是所有可能的解的集合，全局变量x[n]表示解向量，全局变量i表示当前处理的解的层次。

2.递归回溯框架：对应的解空间是所有可能的解的集合，递归函数表示回溯过程，通过递归的方式实现。

3.约束满足问题的回溯法：对应的解空间是满足约束条件的解的集合，约束条件是问题的限制条件，通过回溯的方式搜索满足条件的解。

以上信息仅供参考，如有需要，建议咨询专业程序员。

第5章 回溯法

14
（1）如果X=(x1, x2, …, xi＋1)是问题的最终解，则输出这个解。 如果问题只希望得到一个解，则结束搜索，否则继续搜索其 他解； （2）如果X=(x1, x2, …, xi＋1)是问题的部分解，则继续构造解 向量的下一个分量； （3）如果X=(x1, x2, …, xi＋1)既不是问题的部分解也不是问题 的最终解，则存在下面两种情况： ① 如果xi+1= ai＋1k不是集合Si＋1的最后一个元素，则令xi+1= ai＋ 1k＋1，即选择Si+1的下一个元素作为解向量X的第i+1个分量； ② 如果xi+1= ai＋1k是集合Si＋1的最后一个元素，就回溯到X=(x1, x2, …, xi)，选择Si的下一个元素作为解向量X的第i个分量，假 设xi= aik，如果aik不是集合Si的最后一个元素，则令xi= aik＋1； 否则，就继续回溯到X=(x1, x2, …, xi－1)； 15
2 3
4
3
4
1
3ห้องสมุดไป่ตู้
1
4
2
4
1
2
1
2
3
3
1
2
1
10 12 15 17 21 23 26 28 31 33 37 39 42 44 47 49 52 54 57 59 62 64 n=4的TSP问题的解空间树
8
解空间树的动态搜索（1）
回溯法从根结点出发，按照深度优先策略遍历 解空间树，搜索满足约束条件的解。 在搜索至树中任一结点时，先判断该结点对应 的部分解是否满足约束条件，或者是否超出目标函 数的界，也就是判断该结点是否包含问题的（最优） 解，如果肯定不包含，则跳过对以该结点为根的子 树的搜索，即所谓剪枝（ Pruning ）；否则，进入 以该结点为根的子树，继续按照深度优先策略搜索。

算法第5章回溯法

–
A C此r=时CAr-、w1B=为14活，结V=点V，+vB1=成4为5 当前扩展结点
扩展B，先到达D 再扩• 展CBr<到w达2，ED导致一个不可行解，回溯到B
Cr=C=30，V=0
• E可行，此时A、B、E是活结点，E成为新的扩展结点
• 扩展E，先到达J
B w =16，v =45 C C =30，V=0 • 再次––扩展C由r<E于w到K3，达是JK叶导1结致点一，个即不得可到行一1解个，可回行溯解到xE=(1,0,0)，V=45
3

J 不可行解 V=45 C =0，V=50 再扩•• 展C扩Cr=展到3G0达，，GV先=到0，达活N结，点N是为叶A、结C点、，G且，2G5<为5当0，前不扩是展最结优点解，又N不可r扩展，返回到G
x=(1,0,0) 50>45 • 再扩展G到达O，O是叶结点，且0<50，不是最优解，又O不可扩展，返回到G
if (legal(t)) backtrack(t+1); swap(x[t], x[i]);//回溯还原
}
}
回溯法搜索
排列树的一
般算法
5.2 装载问题
有n个集装箱要装上2艘n载重量分别为c1和c2的轮船，其中集
装箱i的重量为wi，且 wi c1 c2 i 1
✓问题:是否有一个合理的装载方案,可将这n个集装箱装上这2
不可行解 V=45 – 25<50 –
CL是r=C叶r-结w3点=0，，且V5=0V>+4v53=，5皆0 得到一个可行解x=(0,1,1)，V=50
M – L不可扩展，成为死结点，返回到F
不是 • 再扩展F到达M
–
– M是叶结点，且25<50，不是最优解
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5
示例1 0-1背包问题
n=3, C=30, w={16, 15, 15}, v={45, 25, 25}
开始时，Cr=C=30，V=0，A为唯一活结点，也是当前扩展结点 扩展A，先到达B结点 Cr=Cr-w1=14，V=V+v1=45 此时A、B为活结点，B成为当前扩展结点 r 扩展B，先到达D • Cr<w2，D导致一个不可行解，回溯到B 再扩展B到达E • E可行，此时A、B、E是活结点，E成为新的扩展结点 • 扩展E，先到达J 1 1 r • Cr<w3，J导致一个不可行解，回溯到E • 再次扩展E到达K r • 由于K是叶结点，即得到一个可行解 x=(1,0,0)，V=45 • K不可扩展，成为死结点，返回到E • E没有可扩展结点，成为死结点，返回到B B没有可扩展结点，成为死结点，返回到A 2 2 A再次成为扩展结点，扩展 A到达C r 2 r Cr=30，V=0，活结点为A、C，C为当前扩展结点 r 扩展C，先到达F • Cr=Cr-w2=15，V=V+v2=25，此时活结点为A、C、F，F成为当前扩展结点 • 扩展F，先到达L • Cr=Cr-w3=0，V=V+v3=50 • L是叶结点，且50>45，皆得到一个可行解x=(0,1,1)，V=50 • L不可扩展，成为死结点，返回到F • 再扩展F到达M r 3 r 3 • M是叶结点，且 25<50，不是最优解 • M不可扩展，成为死结点，返回到F r • F没有可扩展结点，成为死结点，返回到C 再扩展C到达G • Cr=30，V=0，活结点为A、C、G，G为当前扩展结点 • 扩展G，先到达N，N是叶结点，且25<50，不是最优解，又N不可扩展，返回到G • 再扩展G到达O，O是叶结点，且0<50，不是最优解，又O不可扩展，返回到G • G没有可扩展结点，成为死结点，返回到C C没有可扩展结点，成为死结点，返回到A A没有可扩展结点，成为死结点，算法结束，最优解X=(0,1,1)，最优值V=50
A
C =C=30，V=0
B
w =16，v =45 C =14，V=45
C C =30，V=0

C <w C =14 D E V=45 不可行解
Hห้องสมุดไป่ตู้
25<50 M 不是 C =14 w =15，v3=25 最优 C <w K L J V=45 C =0，V=50 不可行解 解 x=(1,0,0) 50>45 I x=(0,1,1)
4
二、回溯法的基本思想
搜索从开始结点（根结点）出发，以深度优先搜索 整个解空间。 这个开始结点成为活结点，同时也成为当前的扩展 结点。在当前的扩展结点处，搜索向纵深方向移至 一个新结点。这个新结点就成为新的活结点，并成 为当前扩展结点。 如果在当前的扩展结点处不能再向纵深方向扩展， 则当前扩展结点就成为死结点。 此时，应往回移动（回溯）至最近的一个活结点处 ，并使这个活结点成为当前的扩展结点；直到找到 一个解或全部解。
6
w =15，v =25 F C =15，V=25

三、回溯法的基本步骤
回溯法的基本步骤：
(1)针对所给问题，定义问题的解空间； (2)确定易于搜索的解空间结构； (3)以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无 效搜索。
5.1 回溯法的算法框架
本节介绍回溯法算法框架的有关问题： 一、回溯法概述 二、回溯法的基本思想 例子：示例一 三、回溯法的基本步骤 例子：示例二 四、递归回溯 五、迭代回溯 六、子集树与排列树
1
一、回溯法概述
寻找问题的解的一种可靠的方法是首先列出所有候选解，然后依次检查 每一个，在检查完所有或部分候选解后，即可找到所需要的解。理论上 ，当候选解数量有限并且通过检查所有或部分候选解能够得到所需解时 ，上述方法是可行的。不过，在实际应用中，很少使用这种方法，因为 候选解的数量通常都非常大（比如指数级，甚至是大数阶乘），即便采 用最快的计算机也只能解决规模很小的问题。因此需要寻找提高候选解 检查效率的方法。 对候选解进行系统检查的方法有多种，其中回溯法和分支限界法是比较 常用的两种方法。按照这两种方法对候选解进行系统检查通常会使问题 的求解时间大大减少（无论对于最坏情形还是对于一般情形）。事实上 ，这些方法可以使我们避免对很大的候选解集合进行检查，同时能够保 证算法运行结束时可以找到所需要的解。因此，这些方法通常能够用来 求解规模很大的问题。
3
生成问题状态的基本方法
扩展结点：一个正在产生儿子的结点称为扩展结点 活结点：一个自身已生成但其儿子还没有全部生成的节点称 做活结点 死结点：一个所有儿子已经产生的结点称做死结点 深度优先的问题状态生成法：如果对一个扩展结点R，一旦 产生了它的一个儿子C，就把C当做新的扩展结点。在完成 对子树C（以C为根的子树）的穷尽搜索之后，将R重新变成 扩展结点，继续生成R的下一个儿子（如果存在） 宽度优先的问题状态生成法：在一个扩展结点变成死结点之 前，它一直是扩展结点 回溯法：为了避免生成那些不可能产生最佳解的问题状态， 要不断地利用限界函数(bounding function)来处死那些实际上 不可能产生所需解的活结点，以减少问题的计算量。具有限 界函数的深度优先生成法称为回溯法。
2
一、回溯法概述
回溯法是一个既带有系统性又带有跳跃性的搜索算法。 系统性------它以解空间树的形式表示所求问题。在解空间树中，按深 度优先策略，从根结点出发进行搜索解空间树。 跳跃性------搜索进行至解空间树的任一结点时，先判断该结点是否包 含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的搜索，逐 层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。 回溯法求问题的所有解时，要回溯到根，且根结点的所有子树都被搜索 遍才结束。回溯法求问题的一个解时，只要搜索到问题的一个解就可结 束。 这种以深度优先方式系统搜索问题解的算法称为回溯法，它适用于求解 组合数较大的问题。