电工技术--第四章 正弦交流电路
- 格式:doc
- 大小:1.12 MB
- 文档页数:31

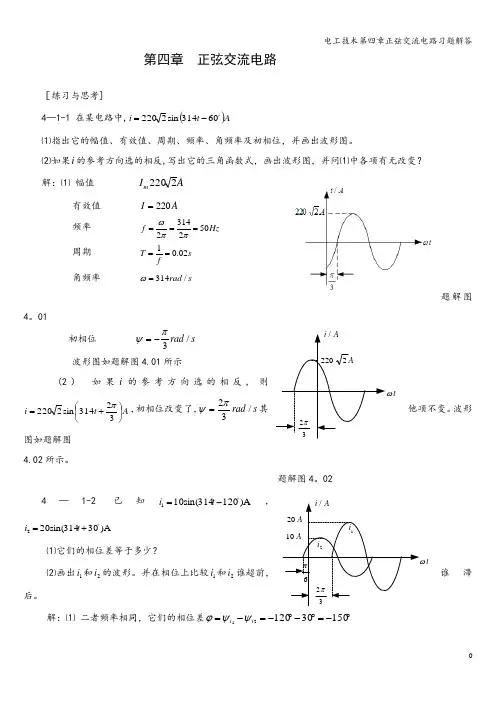
tωAi /A222032πtAi /A 2032π6πA102i 1i 第四章 正弦交流电路[练习与思考]4—1-1 在某电路中,()A t i 60 314sin 2220-=⑴指出它的幅值、有效值、周期、频率、角频率及初相位,并画出波形图。
⑵如果i 的参考方向选的相反,写出它的三角函数式,画出波形图,并问⑴中各项有无改变? 解:⑴ 幅值 A I m 2220有效值 A I 220=频率 3145022f Hz ωππ===周期 10.02T s f==角频率 314/rad s ω=题解图4。
01初相位 s rad /3πψ-=波形图如题解图4.01所示 (2) 如果i 的参考方向选的相反, 则At i ⎪⎭⎫ ⎝⎛+=32 314sin 2220π,初相位改变了,s rad /32πψ=其他项不变。
波形图如题解图 4.02所示。
题解图4。
024—1-2已知A)120314sin(101 -=t i ,A )30314sin(202+=t i⑴它们的相位差等于多少?⑵画出1i 和2i 的波形。
并在相位上比较1i 和2i 谁超前,谁滞后。
解:⑴ 二者频率相同,它们的相位差︒-=︒-︒-=-=1503012021i i ψψϕ+1+1(2)在相位上2i 超前,1i 滞后。
波形图如题解图4.03所示。
题解图4。
03 4—2—1 写出下列正弦电压的相量V )45(sin 2201 -=t u ω,)V 45314(sin 1002 +=t u 解:V U ︒-∠=•4521101 V U ︒∠=•4525024-2-2 已知正弦电流)A60(sin 81 +=t i ω和)A 30(sin 62 -=t i ω,试用复数计算电流21i i i +=,并画出相量图.解:由题目得到A j j j j I I I m m m ︒∠=+=-++=︒-︒+︒+︒=︒-∠+︒∠=+=•••1.231093.32.9)32.5()93.64()30sin 630cos 6()60sin 860cos 8(30660821 所以正弦电流为)A 1.23(sin 101 +=t i ω题解图4.04 相量图如题解图4.04所示。




正选交流电路+三相交流电知识点整理(1)1、正选交流电与直流电的区别所谓正弦交流电路,是指含有正弦电源(激励)而且电路各部分所产生的电压和电流(响应)均按正弦规律变化的电路。
交流发电机中所产生的电动势和正弦信号发生器所输出的信号电压,都是随时间按正弦规律变化的。
它们是常用的正弦电源。
在生产上和日常生活中所用的交流电,一般都是指正弦交流电。
因此,正弦交流电路是电工学中很重要的一个部分。
直流电路:除在换路瞬间,其中的电流和电压的大小与方向(或电压的极性)是不随时间而变化的,如下图所示:正选交流电:正弦电压和电流是按照正弦规律周期性变化的,其波形如下图所示。
正弦电压和电流的方向是周期性变化的。
正弦量:正弦电压和电流等物理量。
正弦量的特征表现在变化的快慢、大小及初始值三个方面,而它们分别由频率(或周期)、幅值(或有效值)和初相位来确定。
所以频率、幅值和初相位就称为确定正弦量的三要素。
2、周期T与频率f周期T:正弦量变化一次所需的时间。
单位:秒(s)频率f:每秒内变化的次数。
单位:赫兹(Hz)两者关系:频率是周期的倒数 f=1/T高频炉的频率是200- 300kHz;中频炉的频率是500-8000Hz;高速电动机的频率是150-2000Hz; 通常收音机中波段的频率是530-1600kHz ,短波段是2.3-23MHz;移动通信的频率是900MHz和1800MHz; 在元线通信中使用的频率可高 300 GHz。
正弦量变化的其他表达方式:角频率正弦量变化的快慢除用周期和频率表示外,还可用角频率ω来表示。
因为一周期内经历了 2π弧度(图 4.1.3) ,所以角频率为:上式表示 T,f,ω三者之间的关系,只要知道其中之一,则其余均可求出。
3、幅值与有效值正弦量在任一瞬间的值称为瞬时值,用小写字母来表示,如 i , U 及 e 分别表示电流、电压及电动势的瞬时值。
瞬时值中最大的值称为幅值或最大值,用带下标 m 的大写字母来表示,如Im, Um 及 Em 分别表示电流、电压及电动势的幅值。


电工与电子技术-正弦交流电路电子教案第一章:正弦交流电路概述1.1 交流电的基本概念1.1.1 交流电的定义1.1.2 交流电的表示方法1.1.3 交流电的产生和传输1.2 交流电路的基本元件1.2.1 电阻元件1.2.2 电感元件1.2.3 电容元件1.3 正弦交流电路的分析方法1.3.1 相量法1.3.2 复数法1.3.3 阻抗法第二章:纯电阻交流电路2.1 欧姆定律适用于交流电路2.1.1 电阻元件的阻抗特性2.1.2 电阻元件的交流电路分析2.2 电阻串联交流电路2.2.1 电压分配定律2.2.2 电流分配定律2.3 电阻并联交流电路2.3.1 电压分配定律2.3.2 电流分配定律第三章:纯电感交流电路3.1 电感元件的交流电路特性3.1.1 感抗的计算3.1.2 电感元件的交流电路分析3.2 电感串联交流电路3.2.1 电压分配定律3.2.2 电流分配定律3.3 电感并联交流电路3.3.1 电压分配定律3.3.2 电流分配定律第四章:纯电容交流电路4.1 电容元件的交流电路特性4.1.1 容抗的计算4.1.2 电容元件的交流电路分析4.2 电容串联交流电路4.2.1 电压分配定律4.2.2 电流分配定律4.3 电容并联交流电路4.3.1 电压分配定律4.3.2 电流分配定律第五章:电阻、电感、电容组合的交流电路5.1 串并联交流电路的分析方法5.1.1 串并联电阻的交流电路分析5.1.2 串并联电感的交流电路分析5.1.3 串并联电容的交流电路分析5.2 交流电路的功率计算5.2.1 有功功率5.2.2 无功功率5.2.3 视在功率5.3 交流电路的相位关系5.3.1 相位差的计算5.3.2 相位关系的分析第六章:交流电路的谐振6.1 谐振条件6.1.1 串联谐振6.1.2 并联谐振6.2 谐振电路的特点6.2.1 电压和电流的幅值6.2.2 功率分配6.3 谐振电路的应用6.3.1 滤波器6.3.2 选频电路6.3.3 谐振器的制作与测试第七章:非正弦交流电路7.1 非正弦交流电的来源7.1.1 电源的非正弦波形7.1.2 电路中的非正弦波形7.2 非正弦交流电的分析方法7.2.1 傅里叶级数分解7.2.2 傅里叶变换的应用7.3 非正弦交流电路的功率计算7.3.1 平均功率的计算7.3.2 无功功率与视在功率的计算第八章:交流电路的测量与测试8.1 交流电压的测量8.1.1 示波器8.1.2 交流电压表的使用8.2 交流电流的测量8.2.1 电流表的使用8.2.2 电流互感器的使用8.3 交流电路的频率响应测试8.3.1 频率响应的定义8.3.2 频率响应的测量方法第九章:三相交流电路9.1 三相电源的产生9.1.1 星形连接9.1.2 三角形连接9.2 三相负载的连接方式9.2.1 YY连接9.2.2 YD连接9.2.3 DY连接9.3 三相电路的功率计算9.3.1 有功功率的计算9.3.2 无功功率的计算9.3.3 视在功率的计算第十章:电工测量与安全10.1 电工测量工具的使用10.1.1 兆欧表10.1.2 钳形电流表10.1.3 多功能电表10.2 电工安全常识10.2.1 触电防护10.2.2 电气火灾预防10.2.3 安全操作规程重点和难点解析一、正弦交流电路概述:理解交流电的基本概念、表示方法和产生传输过程。


tωi /A222032πtωi /A 2032π6πA102i 1i 第四章 正弦交流电路[练习与思考]4-1-1 在某电路中,()A t i 60 314sin 2220-=⑴指出它的幅值、有效值、周期、频率、角频率及初相位,并画出波形图。
⑵如果i 的参考方向选的相反,写出它的三角函数式,画出波形图,并问⑴中各项有无改变? 解:⑴ 幅值 A I m 2220有效值 A I 220= 频率 3145022f Hz ωππ===周期 10.02T s f== 角频率 314/rad s ω=题解图4.01 初相位 s rad /3πψ-=波形图如题解图4.01所示(2) 如果i 的参考方向选的相反, 则A t i ⎪⎭⎫ ⎝⎛+=32 314sin 2220π,初相位改变了,s r a d /32πψ=其他项不变。
波形图如题解图4.02所示。
题解图4.024-1-2 已知A )120314sin(101 -=t i ,A )30314sin(202 +=t i ⑴它们的相位差等于多少?⑵画出1i 和2i 的波形。
并在相位上比较1i 和2i 谁超前,谁滞后。
解:⑴ 二者频率相同,它们的相位差︒-=︒-︒-=-=1503012021i i ψψϕ (2)在相位上2i 超前,1i 滞后。
波形图如题解图4.03所示。
题解图4.03+1+j1m I ∙2m I ∙mI ∙︒60︒30︒1.234-2-1 写出下列正弦电压的相量V )45(sin 2201 -=t u ω,)V 45314(sin 1002 +=t u解:V U ︒-∠=∙4521101 V U︒∠=∙4525024-2-2已知正弦电流)A 60(sin 81 +=t i ω和)A 30(sin 62 -=t i ω,试用复数计算电流21i i i +=,并画出相量图。
解:由题目得到Aj j j j I I I m m m ︒∠=+=-++=︒-︒+︒+︒=︒-∠+︒∠=+=∙∙∙1.231093.32.9)32.5()93.64()30sin 630cos 6()60sin 860cos 8(30660821所以正弦电流为)A 1.23(sin 101 +=t i ω题解图4.04 相量图如题解图4.04所示。
第四章正弦交流电
参考教法
四、应用举例:
[1]已知u = 311sin(314t- 30︒) V,I = 5sin(314t+ 60
的相位差为:ϕui = (-30︒) - (+ 60︒) = - 90︒
即u比i滞后90︒,或i比u超前90︒。
正弦交流电流i = 2sin(100πt- 30︒) A,如果交流电流
的电阻时,电流的最大值、有效值、角频率、频率、周期及初相并求电功率
j2 = -1,j3 = - j
比较电容、电感相位关系及相量图形式区别 强调电容电压滞后电流:理解电容电压与充电关系 电感电压超前电流:理解电感阻碍电流的变化
已知一电容C = 127 μF ,外加于电容两端的正弦交流电压表达V )20314sin( +t ,试求:(1) 容抗X ;(2) 电流大小
串联电路。
又可简化计算。
电流有效值相量:
由
四.提高功率因数的方法
提高感性负载功率因数的最简便的方法,是用适当容量的电容器与感性负载并联,这样就可以使电感中的磁场能量与电容器的电场能量进的电场能量进行交换,从而减少电源与负载间能量的互换。
在感性负载两端并联一个适当的电容后,对提高电路的功率因数十分有效。
借助相量图分析方法容易证明:对于额定电压为U、额定功率为
f的感性负载R-L来说,将功率因数从λ= cos。
电工技术--第四章正弦交流电路第四章正弦交流电路一、内容提要本章主要讨论正弦交流电的基本概念和基本表示方法,并从分析R、L、C各单一参数元件在交流电路中的作用入手,进而分析一般的R、L、C混联电路中电压和电流的关系(包括数值和相位)及功率转换问题。
最后对于电路中串联和并联的谐振现象也作概括的论述。
交流电路不仅是交流电机和变压器的理论基础,同时也要为电子电路做好理论准备,它是工程技术科学研究和日常生活中经常碰到的。
所以本章是本课程中重要的内容之一。
二、基本要求1、对正弦交流电的产生作一般了解;2、掌握正弦交流电的概念;3、准确理解正弦交流电的三要素、相位差及有效值的定义及表达式;4、掌握正弦交流电的各种表示方法及相互间的关系;5、熟悉各种交流电气元件及才参数;6、在掌握单一参数交流电路的基础上,重点掌握R 、L 、C 串、并联电路的分析与计算方法;7、掌握有用功功率和功率因数的计算,了解瞬时功率、无功功率、视在功率的概念8、理解提高功率因数的意义;掌握如何提高功率因数;9、了解谐振电路的特性。
三、 学习指导1. 正弦量的参考方向和相位1)、大小和方向随时间按正弦函数规律变化的电流或电压称为正弦交流电。
正弦交流电的参考方向为其正半周的实际方向。
2)、正弦交流电的三要素一个正弦量是由频率(或周期)、幅值(或有效值)和初相位三个要素来确定。
(1)频率与周期:正弦量变化一次所需的时间(S )称为周期T 。
每秒内变化的次数称为频率f,单位:ZH 。
频率与周期的关系为:T f 1角频率ω:每秒变化的弧度,单位:s rad /。
f T ππω22==(2)幅值与有效值瞬时值:正弦量在任一时刻的值,用i u e ,,表示。
幅值(或最大值):瞬时值中的最大值,用m m m I U E ,,表示。
有效值:一个周期内,正弦量的有效值等于在相同时间内产生相同热量的直流电量值,用I U E ,,表示。
幅值与有效值关系:I I U U E E m m m 2,2,2===。
注意:符号不能混用。
(3)初相位:正弦量的相位(it ϕω+)是反映正弦量变化进程的,初相位用来确定正弦量的初始值。
画波形图时,如果初相位为正角,t=0时的正弦量值应为正半周,从t=0点向左,到向负值增加的零值点之间的角度为初相位的大小;如果初相位为负角,t=0时的正弦量值应在负半周 ,从t=0向右,到向正值增加的零值点之间的角度为初相位的大小。
相位差:两个同频率的正弦量的相位之差等于初相位之差。
21ϕϕϕ-=2. 相量表示应注意:相量只能表示正弦量,而不能等于正弦量。
只有正弦周期量才能用相量表示,否则,不可以用;只有同频率的正弦量才能画在同一向量图上,否则,不可以。
倘若画在一起则无法进行比较与计算的。
3.“j ”的数学意义和物理意义1)、数学意义:1-=j 是虚数单位2)、物理意义:j 是旋转090的算符,即任意一个相量乘以±j 后,可使其旋转±90度。
4. 电压与电流间的关系各种形式的电压与电流间的关系式,是在电压、电流的关联方向下列出的,否则,式中带负号。
5. R 、L 、C 串联电路中,当R ≠O 时,LX 与C X 的大小对于电路的性质有一定影响。
1)、当C L X X>,则C L U U >,0>ϕ电路中的电流将滞后于电路的端电压(感性电路); 2)、当C L X X <,则CL U U <,0=ϕ,电路中的电流将超前于电路的端电压(容性电路)6. R 、L 、C 并联电路在R 、L 、C 并联电路中,当电路的参数和电源的频率使得;1)、C L 11X X >时,则C L I I >,0>ϕ,电路的总电流滞后于电路的端电压(感性电路)2)、C L 11X X <时,则C L I I <,0<ϕ,电路的总电流超前于电路的端电压(容性电路); 3)、C L 11X X =时,则C L I I =,0=ϕ,电路的总电流与电路的端电压同相(电阻性电路)---并联谐振。
7. 在R 、L 、C 电路中,如何选择参考相量 一般情况下,选公共量或已知量作为参考相量,比如在R 、L 、C 串联电路中通常选电流作为参考相量;在R 、L 、C 并联电路中,通常选电压作为参考相量。
但在已知某个电气量的情况下,应选其作为参考相量。
参考相量选定之后,即可由电路中参数的性质及其电压电流的相位关系画出相量图。
8. 复杂正弦交流电路的分析与计算在复杂的文正弦交流电路中,将电压和电流用相量表示之后,即可用支路电流法、回路电流法、节电电压法、叠加原理、戴维南定理和诺顿定理等方法进行分析与计算。
9. 谐振在具有电感和电容元件的交流电路中,通过调节电路的参数或电源的频率而使电压与电流同相,这时电路中就发生谐振现象(分为串联谐振和并联谐振)。
1)、串联谐振条件C L X X =或fC fL ππ212=LC f π210=, LC 10==ωω,0arctan C L =-=R X X ϕ2)、串联谐振的特性(1)电路的阻抗|Z|=2C L 2)(X X R -+=R ,其值最小。
在U 不变得情况下,电流最大,==0I I R U 。
(2)ϕ=0(电源电压与电路中电流同相),电路对电源呈现电阻性。
电源供给电路的能量全部被电阻所消耗,电源与电路之间不发生能量的互换,能量的互换只发生在电感线圈与电容器之间。
(3)|L •U |=|C•U |且在相位上相反,互相抵消,对整个电路不起作用,因此RU U ••=。
但L L L X RU IX U ==及C C C X R U IX U ==的单独作用不容忽视(因为当R X X >=C L 时,UU U >=C L ,电压过高可能会击穿线圈或电容器的绝缘)。
串联谐振也称电压谐振。
电力工程中一般应避免之。
3)、品质因数R L CR U U U U Q 00L C 1ωω====称为电路的品质因数,简称Q值。
其物理意义:(1)表示谐振时电感或电容上的电压是电源电压的Q 倍;(2)值越大,则谐振曲线越尖锐,选择性越强。
4)、通频带宽度 在0021%7.70I I I ==处频率上下限之间的宽度称为通频带宽度,即12f f f -=∆(见图4-1)f1f 0f 2f 0707.0I 0IO 图4-1通频带宽度越小,表明谐振曲线越尖锐,电路的选频性越强;而谐振曲线的尖锐程度与Q 值有关。
5)、并联谐振电路的特性(1)电路发生并联谐振时的频率LC L R LC f ππ21121220≈-= (2)•U 与•I 同相位,电源只供给电阻消耗的有功功率,而无功功率的交换只在电感支路之间进行。
(3)•L I 与•CI 的无功分量相等而相位相反,2C 2L 0I I I -=,当R=0时,0C L I I I >>≈。
(4)在谐振点附近,电路呈现高阻抗值:RC L Z =。
在电压U 保持一定时,则在谐振点附近电流值很小。
10.功率因数的提高1)、交流电路的平均功率为:ϕcos UI p =称为电路的功率因数,它决定于电路(负载)的性质,其值介于0与1之间。
当1cos ≠ϕ时,出现无功功率ϕsin UI Q =,电路中发生能量的互换。
从而引起两个问题:(1) 发电设备的容量不能充分利用;(2)增加线路和发电机绕组的功率损耗。
通常要求功率因数为0.9~0.95。
功率因数不高的原因由于电感性负载的存在,电感性负载的功率因数之所以小于1,是由于负载本身需要一定的无功功率。
提高功率因数的意义在于解决这个矛盾,即减少电源与负载之间的能量互换,又使电感性负载取得所需的无功功率。
按照供用电规则,高压供电负荷平均功率因数不低于0.9,其它负荷不低于0.85。
2)、功率因数的提高提高功率因数常用的方法就是在保持用电设备原有的额定电压、额定电流及功率不变,也即工作状态不变。
在电感性负载并联静电电容器(设备在用户或变电所中),其电路图和相量图如图4-2所示。
图4-2 并联电容器以后,电感性负载的电流2L 211X R I+=和功率因数2L21cos XR R +=ϕ均未变化,这是因为所加电压和负载参数没有改变。
但电压U 和线路电流i 之间的相位差ϕ变小了,即ϕcos 变大了。
这里所讲的提高功率因数,是指提高电源或电网的功率因数,而不是指提高某个电感性负载的功率因数。
因此,在选择静电电容器的容量时,必须了解补偿前同载的平均功率因数,它可根据一年的电能消耗量来计算:2Q2PP 22221)8760()8760(8760cos WW W P Q P PQ PS P +=+=+==ϕ式中P 和Q 分别是年消耗有功率(kW )和无功功率(kvar );PW 和QW 分别为年有功电能消耗量)(h kW ⋅和无功电能消耗量(h k ⋅var ),可由有功电度表和无功电度表读取;8760是全年的总时数。
然后根据下式计算所需静电电容器的容量)tan (tan 1maxϕϕγ-=P Q式中m axP 是负载的最大有功功率;γ是负载系数,一般取0.85;1ϕ是补偿前的相位差;ϕ是补偿后的相位差。
或由相量图4-2b )推出该电容器的电容值)tan (tan 212ϕϕω-=U pC电容器的安装常采用高压集中补偿和低压分散补偿两种方式,也可以二者结合。
P65 练习与思考4.1.1 有效值V 220=U ,ZH 50=f ,6πϕ-=4.1.2 360021πϕϕϕ==-= 4.1.34.1.4 不可用,因为300VV 2220>。
P68 练习与思考 4.2.1 V6060V,)30sin 30(cos 22002001∠=+=••U j U4.2.2 (1)A10A,)30cos(100300j me It i =+=•ω (2)V452200∠=•U(3) A5030j m e I =•P71 练习与思考ϕiiωφiu ,练习 4.1.3φφ4.3.1,对错,L C ,X IUX i u ==,错对,)(L Cj Ij ,U dt di Lt uω-==4.3.2 由于dtdi Lt uLL )(=,所谓感抗LXω=L,它反映阻值与自感系数、频率都有关系;对直流(0=ω)相当短路。
4.3.3 由于dtdu Ct iC C )(=,所谓容抗CXω1C=,它反映阻值与电容的大小、频率都有关系;对交流(∞→ω)相当端路,对直流(0=ω)相当开路。
4.3.4 a)不变 b)i 量值减小 c) i 量值增大P76 练习与思考4.4.1错)()1(C L C L R X X I IR U U U U ++=++=错)(•••=Z I U 2对)(对ZU I ZU I ••==4)3( 错)(RCL ωωϕ-=arctan5对))(()6(C L X X j R I U -+=••4.4.2 错,两并联电路电流的大小为4A ,由于不在同一直线上,因此不可以直接相加。