圆锥曲线地第三定义
- 格式:doc
- 大小:540.25 KB
- 文档页数:11

椭圆的第一定义第二定义第三定义
椭圆的第一二三定义:
第一定义:平面内与两定点F1,F2的距离的和等于常数2a (2a>|F1F2|)的动点P的轨迹叫做椭圆。
第二定义:平面内到定点f的距离与到定直线的距离之比为常数e(即椭圆的离心率,e=c/a)地点的集合(定点f不在定直线上,该常数为小于1的正数)。
第三定义:椭圆上的点与椭圆短轴两端点连线的斜率之积是定值,定值为e^2-1.
椭圆是圆锥曲线的一种,即圆锥与平面的截线。
椭圆的周长等于特定的正弦曲线在一个周期内的长度。

圆锥曲线第三定义简介
---------------------------------------------------------------------- 第三定义:
只有椭圆和双曲线有第三定义即椭圆或双曲线上一动点(两顶点除外)与两顶点(a,0)(-a,0)或(0,a)(0,-a)连线的斜率的乘积为定值e^2-1。
圆锥曲线,是由一平面截二次锥面得到的曲线。
圆锥曲线包括椭圆(圆为椭圆的特例)、抛物线、双曲线。
起源于2000多年前的古希腊数学家最先开始研究圆锥曲线。
圆锥曲线(二次曲线)的(不完整)统一定义:到平面内一定点的距离r与到定直线的距离d之比是常数e=r/d的点的轨迹叫做圆锥曲线。
其中当e>1时为双曲线,当e=1时为抛物线,当0<e<1时为椭圆。
定点叫做该圆锥曲线的焦点,定直线叫做(该焦点相应的)准线,e叫做离心率。
【拓展】
第一定义:
平面内与两定点F1、F2的距离的和等于常数2a(2a≥|F1F2|)的动点P的轨迹叫做椭圆。
即:其中两定点F1、F2叫做椭圆的焦点,两焦点的距离|F1F2|=2c≤2a叫做椭圆的焦距。
P为椭圆的动点。
第二定义:
椭圆平面内到定点F(c,0)的距离和到定直线l:x=a/c(F不在l上)的距离之比为常数从C/A,(即离心率,0<e<1)的点的轨迹是椭圆。
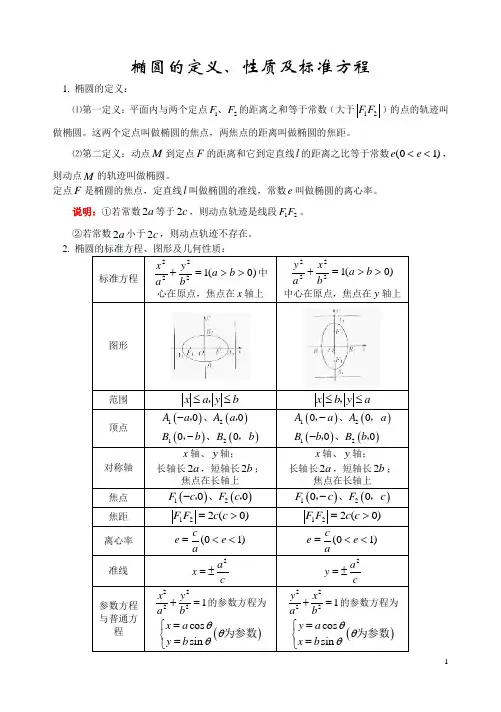
椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①若常数2a 等于2c ,则动点轨迹是线段12F F 。
②若常数2a 小于2c ,则动点轨迹不存在。
2. 椭圆的标准方程、图形及几何性质:标准方程)0(12222>>=+b a by a x 中心在原点,焦点在x 轴上)0(12222>>=+b a b x a y 中心在原点,焦点在y 轴上图形范围 x a y b ≤≤,x b y a ≤≤,顶点()()()()12120000A a A a B b B b --,、,,、,()()()()12120000A a A a B b B b --,、,,、,对称轴 x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上焦点 ()()1200F c F c -,、, ()()1200F c F c -,、, 焦距 )0(221>=c c F F)0(221>=c c F F离心率 )10(<<=e ace )10(<<=e ace 准线2a x c=±2a y c=±参数方程与普通方程22221x y a b +=的参数方程为 ()cos sin x a y b θθθ=⎧⎨=⎩为参数 22221y x a b +=的参数方程为 ()cos sin y a x b θθθ=⎧⎨=⎩为参数3. 焦半径公式:椭圆上的任一点和焦点连结的线段长称为焦半径。

高三数学圆锥曲线的定义(理)人教版知识精讲【同步教育信息】一. 本周教学内容:圆锥曲线的定义二. 重点、难点: 1. 第一定义椭圆:a PF PF 221=+ 双曲线:a PF PF 221=- 2. 第二定义e l P d PF=),(〔1〕)1,0(∈e 为椭圆 〔2〕1=e 为抛物线〔3〕),1(+∞∈e 为双曲线【典型例题】[例1] 求过M 〔2,3-〕且与椭圆14922=+y x 共焦点的〔1〕椭圆方程〔2〕双曲线方程。
解:〔1〕设12222=+b y a x ∴ ⎪⎩⎪⎨⎧==⇒⎪⎩⎪⎨⎧=-=+10155149222222b a b a ba ∴ 1101522=+y x 〔2〕设12222=-b y a x ∴ ⎪⎩⎪⎨⎧==⇒⎪⎩⎪⎨⎧=+=-235149222222b a b a ba ∴ 12322=-y x 另解:14922=-+-λλy x ∴ 14499=-+-λλ ∴ 6±=λ ∴ 6=λ时,双曲线12322=-y x 6-=λ时,椭圆1101522=+y x[例2]〔1〕P 为椭圆)0(12222>>=+b a by a x 上一点,P 不在x 轴上,21F F 为焦点,α=∠21PF F ,求21PF F S ∆;〔2〕P 为双曲线)0,0(12222>>=-b a by a x 上一点,P 不在x 轴上,21,F F 为焦点,α=∠21PF F ,求21PF F S ∆。
解:〔1〕221222142a PF PF PF PF =⋅++22122214cos 2c PF PF PF PF =⋅-+α ∴ 2214)cos 1(2b PF PF =+⋅α∴ αcos 12221+=⋅b PF PF∴ αsin 212121⋅⋅⋅=∆PF PF S F PF 2tan cos 1sin 22αααb b =+⋅=〔2〕221222142a PF PF PF PF =-+ 22122214cos 2c PF PF PF PF =⋅⋅-+α∴ 2214)cos 1(2b PF PF =-⋅⋅α αcos 12221-=⋅b PF PF∴ 2cot cos 1sin sin 21222121ααααb b PF PF S PF F =-⋅=⋅⋅=∆[例3]〔1〕椭圆M :)0(12222>>=+b a by a x ,P 为M 上一点,︒=∠3021F PF ,12F PF ∠︒=120,求离心率;〔2〕双曲线M :12222=-by a x ,P 为M 上一点,︒=∠1521F PF ,︒=∠7512F PF ,求离心率。

椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①若常数2a 等于2c ,则动点轨迹是线段12F F 。
②若常数2a 小于2c ,则动点轨迹不存在。
2.3. 椭圆上的任一点和焦点连结的线段长称为焦半径。
焦半径公式:椭圆焦点在x 轴上时,设12F F 、分别是椭圆的左、右焦点,()00P x y ,是椭圆上任一点,则10PF a ex =+,20PF a ex =-。
推导过程:由第二定义得11PF e d =(1d 为点P 到左准线的距离), 则211000a PF ed e x ex a a ex c ⎛⎫==+=+=+ ⎪⎝⎭;同理得20PF a ex =-。
简记为:左“+”右“-”。
由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数。
22221x y a b +=;若焦点在y 轴上,则为22221y x a b+=。
有时为了运算方便,设),0(122n m m ny mx ≠>=+。
双曲线的定义、方程和性质1. 定义(1)第一定义:平面内到两定点F 1、F 2的距离之差的绝对值等于定长2a (小于|F 1F 2|)的点的轨迹叫双曲线。
说明:①||PF 1|-|PF 2||=2a (2a <|F 1F 2|)是双曲线;若2a=|F 1F 2|,轨迹是以F 1、F 2为端点的射线;2a >|F 1F 2|时无轨迹。
②设M 是双曲线上任意一点,若M 点在双曲线右边一支上,则|MF 1|>|MF 2|,|MF 1|-|MF 2|=2a ;若M 在双曲线的左支上,则|MF 1|<|MF 2|,|MF 1|-|MF 2|=-2a ,故|MF 1|-|MF 2|=±2a ,这是与椭圆不同的地方。

圆锥曲线的定义与性质及其应用圆锥曲线是数学中研究的一类平面曲线,包括椭圆、双曲线和抛物线。
它们具有独特的性质和广泛的应用。
本文将对圆锥曲线的定义、性质以及一些实际应用进行介绍。
1. 圆锥曲线的定义圆锥曲线是在一个平面上,以一点为焦点,一条直线为准线,到该直线上各点的距离与到焦点的距离之比等于一个常数的点构成的曲线。
根据准线与焦点的位置关系,圆锥曲线可以分为三类:椭圆、双曲线和抛物线。
2. 椭圆的性质与应用椭圆是一种闭合的曲线,其定义为到两个焦点距离之和等于常数的点的集合。
椭圆具有以下性质:- 椭圆的长轴和短轴:椭圆的两个焦点之间的距离等于椭圆的长轴,而通过椭圆中心且垂直于长轴的线段称为椭圆的短轴。
- 焦点定理:对于椭圆上的任意一点P,其到两个焦点的距离之和等于椭圆的长轴的长度。
- 在物理学和天文学中,椭圆常用来描述行星、彗星和卫星的轨道。
3. 双曲线的性质与应用双曲线是一种开放的曲线,其定义为到两个焦点距离差的绝对值等于常数的点的集合。
双曲线具有以下性质:- 双曲线的渐近线:双曲线有两条渐近线,其与曲线的距离趋近于零,且曲线无限延伸。
- 双曲线的离心率:双曲线的离心率大于1。
离心率是描述焦点与准线距离关系的重要参数。
- 在物理学中,双曲线常用来描述电磁波的传播和光学系统中的折射现象等。
4. 抛物线的性质与应用抛物线是一种开放的曲线,其定义为到焦点距离等于到准线的距离的点的集合。
抛物线具有以下性质:- 抛物线的对称性:抛物线以焦点为中心,与焦点到准线垂直的线段称为对称轴。
抛物线上的任意一点到焦点和准线的距离相等。
- 抛物线的焦距:焦点到对称轴的距离称为抛物线的焦距,是抛物线性质研究和计算的重要参数。
- 在物理学中,抛物线常用来描述抛射物的运动轨迹,以及天文学中的天体运动等。
5. 圆锥曲线的应用举例圆锥曲线在科学和工程领域具有广泛的应用,以下举几个例子:- 天体运动:行星、彗星和卫星的轨道通常用椭圆来描述,能够帮助科学家研究它们的运动规律。

圆曲第三定义证明一般来说,曲线的定义方法和曲线上的点的性质是等价的,所以可以用满足一定性质的点的轨迹来定义曲线。
掌握了这些曲线的性质和定义方法除了对完成解析几何的题目有帮助之外还可以对解三角形、平面向量的题目有启发作用。
下面就来看一看我们熟悉的图形有哪些我们不熟悉的定义方法。
(注:一下讨论内容均在同一平面内)1.圆(1)到定点距离为定值的点的集合为圆。
最基本的定义,不多说了(2)到两不同定点距离比值为定值(不为1)的点的集合用代数语言描述就是:设 [公式] ,动点P满足 [公式] ,设P的坐标是 [公式]则 [公式] ,平方后移项展开得到 [公式]代入圆的一般方程的判别式知判别式大于0,所以P点的轨迹方程是圆的方程。
这就是大名鼎鼎的阿波罗尼亚斯圆了。
(3)到两定点连线夹角为直角的点的集合设 [公式] ,动点P 满足 [公式]这种定义还有其他两个说法: [公式] ,以及 [公式]注意一下这三种定义并不完全等价,当用斜率以及角来定义P的轨迹时,P的轨迹是不包含A,B两点的,但是当用向量的内积来定义时轨迹是包含A,B两点的。
但是这三种定义方法大概是差不多的(毕竟P与A或B重合没啥研究价值)。
special:到两定点连线夹角为定值(0到 [公式] 之间)的点的集合。
当P点在AB的圆弧上方或者下方移动时, [公式] 可以保持定值,但如果从上方移动到下方那么 [公式] 的值就会变化,就不满足要求了。
即使这种定义方法定义出来的轨迹不是完整的圆,但仍能在做题中帮助我们许多。
2.椭圆(1)到两定点的距离之和为定值的点的集合课本上最基础的定义,不多说了。
(2)到定点的距离与到定直线的距离的比值为定值(介于0和1之间)的点的集合这种定义方法是圆锥曲线的统一定义,也可以叫圆锥曲线的第二定义。
对于圆锥曲线而言,这个定点是焦点,这条定直线称为准线。
对于椭圆 [公式] (a>b>0)而言,其焦点为[公式] ,其准线为[公式]其中半焦距 [公式] ,离心率 [公式]设P为椭圆上一点,P到 [公式] 的距离为 [公式] ,P到 [公式] 的距离为 [公式] ,则有[公式](3)到两定点连线斜率乘积为定值的点的集合(第三定义)如果考虑到上面提到圆的第(3)点,在坐标系内作伸缩变化,那么这就是个很自然的结论。

圆锥曲线第三定义
圆锥曲线的第三定义是指通过取定一个固定点F(焦点)和一个固定线段L
(准线),对于平面内的所有点P,其到焦点F的距离与其到准线L的距离之比始终保持不变。
这个比值称为离心率,用e表示。
根据这个定义,我们可以得到三种不同形状的圆锥曲线,分别是椭圆、双曲线
和抛物线。
对于椭圆来说,焦点和准线之间的距离相等,即e=1。
在平面上的任意一点P 上,PF与PL之比始终为1,这使得椭圆具有对称性。
椭圆的形状与焦点和准线之
间的距离有关,当焦点和准线的距离增大时,椭圆的形状趋向于扁平。
双曲线的离心率大于1,即e>1。
对于双曲线上的任意一点P,PF与PL之比
始终大于1,这使得双曲线具有两个分支,分别向着焦点和准线延伸。
双曲线的形
状与焦点和准线之间的距离有关,当焦点和准线的距离增大时,双曲线的形状趋向于扁平。
抛物线的离心率等于1,即e=1。
对于抛物线上的任意一点P,PF与PL之比
始终为1,这使得抛物线具有对称性。
抛物线的形状与焦点和准线之间的距离有关,当焦点和准线的距离增大时,抛物线的形状趋向于扁平。
通过圆锥曲线的第三定义,我们可以理解不同形状的椭圆、双曲线和抛物线,
并且可以对它们的特点进行分析和比较。
圆锥曲线在数学和物理等领域中有着广泛的应用和研究价值。

-1( a ―0)的长轴长为 例、已知椭圆—2 a ―1直线l 与椭圆相交与 M 、N 两点,记直线 PM 、PN 的斜率分别为kl 、k2。
若k1 k2= - ,4则椭圆的方程为。
变式:1、设点A ,B 的坐标为(-2,0),( 2,0),点P 是曲线C 上任意一点,且直线 PA 与PB 的1斜率之积为-,则曲线C 的方程为。
42、设点P 是曲线C 上任意一点,坐标原点是 0,曲线C 与X 轴相交于两点 M (-2,0),3N (2,0),直线PM ,PN 的斜率之积为-,贝U OP 的最小值是。
4-8,0),( 8,0 ),且AC, BC 所在直线斜率之积为 m ( m ≠0 ),求顶点C 的轨迹。
2 24、P 是双曲线 仔-占=1(a 0,b 0)上一点,M,N 分别是双曲线的左右顶点,直线PM ,a b 1PN 的斜率之积为一,则双曲线离心率为。
X 2 2圆锥曲线第三定义在椭圆—2 1(a ― 0)中,A , B 两点关于原点对称,P 是椭圆上异于 A , B 两 ― 点的任意一点, k pA , k pB 存在,则 k pA * k PB―2r 。
(反之亦成立) a 在双曲线 2爲=1(a 0, ― ■ 0)中,A ,B 两点关于原点对称, ―2 P 是椭圆上异于A , B 两点的任意一点,若 k PA , k PB 存在,则 kPA *k PB b=。
(反之亦成立)a ★焦点在Y 轴上时,椭圆满足 k PA *k PB —a 2双曲线满足k p A ∙k pBa 2b 2X 2 3、已知 ABC 的两个顶点坐标分别是(4,若点P 是椭圆上任意一点,过原点的2 255、已知椭圆——=1的左右顶点分别是A、B, M是椭圆上异于A、B的动点,求证:3 2k MA *k MB为定值。
6、平面内与两定点A i(-a,0),A2(a,0) (a 0)连续的斜率之积等于非零常数m的点的轨迹,加上A、A2两点所成的曲线C可以是圆、椭圆成双曲线.求曲线C的方程,并讨论C 的形状与m值得关系;第三定义的应用2例、椭圆y2=1的左右顶点分别是A, B,点S是椭圆上位于X轴上方的动点,直线AS,410BS与直线l : X 分别交于点M、N,求线段MN长度的最小值。

高三数学圆锥曲线知识点在高中数学中,圆锥曲线是一个重要的概念。
它由圆、椭圆、双曲线和抛物线四种曲线构成。
掌握圆锥曲线的知识对于解决各种数学问题和应用是至关重要的。
本文将介绍高三数学圆锥曲线的知识点。
一、圆锥曲线的定义和性质圆锥曲线是一个平面上到一个定点和一个定直线的距离之比保持不变的点的轨迹。
圆锥曲线分为四种类型:圆、椭圆、双曲线和抛物线。
1. 圆:圆是所有到一个点的距离相等的点的轨迹。
圆的特点是中心坐标为(h, k),半径为r。
2. 椭圆:椭圆是所有到两个定点之和的距离之比为定值的点的轨迹。
椭圆的特点是有两个焦点F1和F2,两个焦点之间的距离为2a,离心率为e,长轴的长度为2a,短轴的长度为2b。
3. 双曲线:双曲线是所有到两个定点之差的距离之差为定值的点的轨迹。
双曲线的特点是有两个焦点F1和F2,两个焦点之间的距离为2a,离心率为e,离心率小于1。
4. 抛物线:抛物线是所有到一个定直线的距离与到一个定点的距离相等的点的轨迹。
抛物线的特点是焦点为F,准线为L,焦距为p,焦点到准线的距离为x,焦点到点P的距离为y。
二、圆锥曲线的方程1. 圆的方程:$(x-h)^2 + (y-k)^2 = r^2$,其中(h, k)为圆心的坐标,r为半径。
2. 椭圆的方程:$\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$,其中(h, k)为椭圆中心的坐标,a和b分别为椭圆长半轴和短半轴的长度。
3. 双曲线的方程:$\frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} =1$,其中(h, k)为双曲线中心的坐标,a和b分别为双曲线长半轴和短半轴的长度。
4. 抛物线的方程:$y^2 = 4ax$,其中焦点为原点,准线为x轴,焦距为p。
三、圆锥曲线的性质和应用1. 圆的性质:圆的切线与半径垂直,圆的弦与半径垂直于弦的中点。
2. 椭圆的性质:椭圆的离心率介于0和1之间,焦点和对称轴平行。

点差法与圆锥曲线第三定义的应用举例尹伟云(贵州省仁怀市周林高中ꎬ贵州仁怀564599)摘㊀要:点差法是解决圆锥曲线中点弦问题的有效工具ꎬ亦是高考的常考对象.本文从点差法入手ꎬ探究点差法与圆锥曲线第三定义的联系ꎬ给出5个经典结论及其证明ꎬ并以实例阐述其应用.关键词:点差法ꎻ中点弦ꎻ圆锥曲线第三定义中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)19-0086-05收稿日期:2023-04-05作者简介:严伟云ꎬ从事高中数学教学研究.㊀㊀圆锥曲线中的中点弦和直径问题是高考经常考查的对象.在某些与中点及直径有关的相交弦问题中ꎬ利用点差法或圆锥曲线第三定义可快速得到两直线的斜率之积ꎬ尤其是在小题中ꎬ直接利用结论求解ꎬ可大大地节省解题时间.下面就这些问题进行探讨.1点差法的原理1.1点差法在椭圆中点弦问题中的应用结论1㊀设直线l(不与坐标轴垂直且不过原点)与椭圆x2a2+y2b2=1(a>b>0)相交于A(x1ꎬy1)ꎬB(x2ꎬy2)两点ꎬP(x0ꎬy0)为弦AB的中点ꎬ如图1ꎬ则kOP kAB=y0x0 kAB=-b2a2=e2-1ꎻ若椭圆方程为y2a2+x2b2=1(a>b>0)ꎬ如图2ꎬ则kOP kAB=y0x0 kAB=-a2b2=1e2-1.证明㊀由x21a2+y21b2=1ꎬx22a2+y22b2=1ꎬìîíïïïï两式相减ꎬ得图1㊀椭圆焦点在x轴㊀㊀㊀㊀㊀图2㊀椭圆焦点在y轴x21-x22a2+y21-y22b2=0.即(x1+x2)(x1-x2)a2+(y1+y2)(y1-y2)b2=0.化为(y1+y2)/2(x1+x2)/2 y1-y2x1-x2=-b2a2.所以y0x0 kAB=-b2a2.故kOP kAB=-b2a2=-a2-c2a2=e2-1.如图2ꎬ当椭圆的焦点在y轴上时ꎬ同理得kOP kAB=y0x0 kAB=-a2b2=1e2-1.1.2点差法在双曲线中点弦问题中的应用结论2㊀设直线l(不与坐标轴垂直且不过原点)与双曲线x2a2-y2b2=1(a>0ꎬb>0)相交于A(x1ꎬy1)ꎬB(x2ꎬy2)两点ꎬP(x0ꎬy0)为弦AB的中点ꎬ如图3和图4ꎬ仿照结论1的证明方法ꎬ容易得到kOP kAB=y0x0 kAB=b2a2=e2-1.若双曲线方程为y2a2-x2b2=1(a>0ꎬb>0)ꎬ则kOP kAB=y0x0 kAB=a2b2=1e2-1.图3㊀双曲线中点弦问题㊀㊀㊀㊀图4㊀双曲线中点弦问题根据结论1和结论2ꎬ容易知道椭圆㊁双曲线中点差法的统一公式:设曲线C:x2m+y2n=1ꎬ其中mnʂ0ꎬ直线l(不与坐标轴垂直且不过原点)与曲线C相交于A(x1ꎬy1)ꎬB(x2ꎬy2)两点ꎬP(x0ꎬy0)为弦AB的中点ꎬ则kOP kAB=-nm.①当m=n>0时ꎬ方程x2m+y2n=1表示圆ꎬ由垂径定理可知ꎬkPA kPB=-1ꎻ②当mʂn且m>0ꎬn>0时ꎬ方程x2m+y2n=1表示椭圆ꎻ③当mn<0时ꎬ方程x2m+y2n=1表示双曲线ꎻ④当m<0ꎬn<0时ꎬ方程x2m+y2n=1不表示任何曲线.1.3点差法在抛物线中点弦问题中的应用结论3㊀设直线l(不与抛物线对称轴垂直)与抛物线y2=2px(p>0)相交于A(x1ꎬy1)ꎬB(x2 y2)两点ꎬP(x0ꎬy0)为弦AB的中点ꎬ如图5ꎬ则y0 kAB=p.若抛物线方程为x2=2py(p>0)ꎬ则x0kAB=p.图5㊀抛物线中点弦问题证明㊀由y21=2px1ꎬy22=2px2ꎬ{两式相减ꎬ得y21-y22=2p(x1-x2).化简为y1+y22 y1-y2x1-x2=p.即得y0 kAB=p.若抛物线方程为x2=2py(p>0)ꎬ同理可证x0kAB=p.2圆锥曲线的第三定义已知AꎬB是x轴上关于原点O对称的两点ꎬ设|AB|=2a.若平面内异于AꎬB的动点P满足kPA kPB为定值λꎬ则当-1<λ<0时ꎬ点P的轨迹为椭圆(不含长轴端点AꎬB)ꎬ设短轴长为2bꎬ则λ=-b2a2ꎻ当λ>0时ꎬ点P的轨迹为双曲线(不含实轴端点AꎬB)ꎬ设虚轴长为2bꎬ则λ=b2a2.由上知ꎬλ=e2-1ꎬ其中e为对应轨迹的离心率.将圆锥曲线第三定义进行推广ꎬ得到如下结论:结论4㊀如图6ꎬ过原点的直线与椭圆x2a2+y2b2=1(a>b>0)相交于AꎬB两点ꎬP为椭圆上异于AꎬB的动点ꎬ当直线PAꎬPB的斜率均存在时ꎬ有kPA kPB=e2-1=-b2a2.当椭圆的焦点在y轴上时ꎬ有kPA kPB=1e2-1=-a2b2.证法1㊀设P(x0ꎬy0)ꎬA(x1ꎬy1)ꎬ则B(-x1ꎬ图6㊀结论4图-y1)ꎬ从而直线PAꎬPB的斜率之积为kPA kPB=y0-y1x0-x1y0+y1x0+x1=y20-y21x20-x21=b21-(x20/a2)[]-b21-(x21/a2)[]x20-x21=-b2a2.证法2㊀取AP的中点Mꎬ连接OMꎬ由点差法ꎬ得kPA kPB=kPA kOM=e2-1=-b2a2.当椭圆的焦点在y轴上时ꎬ同理可证kPA kPB=1e2-1=-a2b2.结论5㊀如图7ꎬ过原点的直线与双曲线x2a2-y2b2=1(a>0ꎬb>0)相交于AꎬB两点ꎬP为双曲线上异于AꎬB的动点ꎬ当直线PAꎬPB的斜率均存在时ꎬ有kPA kPB=e2-1=b2a2.图7㊀结论5图当双曲线的焦点在y轴上时ꎬ有kPA kPB=1e2-1=a2b2.证法1㊀设P(x0ꎬy0)ꎬA(x1ꎬy1)ꎬ则B(-x1ꎬ-y1)ꎬ则kPA kPB=y0-y1x0-x1y0+y1x0+x1=b2(x20/a2)-1[]-b2(x21/a2)-1[]x20-x21=b2a2.证法2㊀取PA的中点Mꎬ连接OMꎬ由点差法ꎬ得kPA kPB=kPA kOM=e2-1=b2a2.当椭圆的焦点在y轴上时ꎬ同理可证kPA kPB=1e2-1=a2b2.3实例分析例1㊀已知椭圆C:x24+y2=1上存在两点AꎬB关于直线l:x=my+1对称ꎬ则实数m的取值范围是.解析㊀由题意知ꎬ直线AB与l互相垂直ꎬ所以kAB kl=-1ꎬ得kAB=-m.设线段AB的中点为M(x0ꎬy0)ꎬ由点差法ꎬ得kAB kOM=-b2a2.即(-m)y0x0=-14.与x0=my0+1联立ꎬ得x0=43ꎬy0=13m.ìîíïïïï因为点M43ꎬ13mæèçöø÷在椭圆C的内部ꎬ所以164ˑ9+13mæèçöø÷2<1.解得m>55ꎬ或m<-55.所以实数m的取值范围是-¥ꎬ-55æèçöø÷ɣ55ꎬ+¥æèçöø÷.评注㊀在椭圆中ꎬ由点差法得到的式子 kABkOM=-b2a2 是相交弦中点与原点连线的斜率与弦所在直线斜率的一个等量关系.kAB与直线AB直接相关联ꎬ-b2a2与椭圆C相关联ꎬ因此ꎬ点差法搭建了直线与椭圆之间的桥梁.在本题中ꎬ点差法为弦中点的表示创造了重要条件ꎬ从而通过中点与椭圆的位置关系建立不等关系.例2㊀已知F1(-cꎬ0)ꎬF2(cꎬ0)分别为双曲线C:x2a2-y2b2=1(a>0ꎬb>0)的左㊁右焦点ꎬ直线l:xc+yb=1与C交于MꎬN两点ꎬ线段MN的垂直平分线与x轴交于点T(-5cꎬ0)ꎬ则C的离心率为.解析㊀设线段MN与其垂直平分线交于点Pꎬ连接OPꎬ如图8.图8㊀例2解析图则kPT kMN=-1ꎬkOP kMN=b2a2.ìîíïïï①②两式相比ꎬ得kPTkOP=-a2b2.即y0x0+5c x0y0=-a2b2ꎬ解得x0=-5a2c.又由①得y0x0+5c -bcæèçöø÷=y0-5a2/c+5c -bcæèçöø÷=-1.解得y0=5b.将x0=-5a2cꎬy0=5bꎬìîíïïï代入xc+yb=1中ꎬ得-5a2c2+5bb=1.化简为c2a2=54.所以e=ca=52.评注㊀求离心率的关键是找到关于aꎬbꎬc的一个齐次等量关系ꎬ而点差法的结论 kOP kMN=b2a2 中恰好含有a与b的齐二次关系.对于结论中两直线的斜率ꎬ一般有两种转化途径:一是转化为点的坐标ꎬ二是利用几何图形的特征或位置关系进行转化.本题就是通过点的坐标以及两直线的垂直关系与点的共线关系进行转化.例3㊀抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后ꎬ沿平行于抛物线对称轴的方向射出.今有抛物线C:x2=8yꎬ如图9ꎬ一平行于y轴的光线从上方射向抛物线上的点Pꎬ经抛物线2次反射ꎬ最后从抛物线上的点Q沿平行于y轴方向射出.若直线l:y=x+m与抛物线C交于AꎬB两点ꎬ在坐标平面内作әABNꎬ使әABN的外接圆圆心的坐标为I-12ꎬ11æèçöø÷ꎬ求弦AB的长度.图9㊀例3解析图解析㊀设A(x1ꎬy1)ꎬB(x2ꎬy2)ꎬ线段AB的中点为M(x0ꎬy0)ꎬ则x21=8y1ꎬx22=8y2.两式相减ꎬ得x21-x22=8(y1-y2).化简为x1+x22=4(y1-y2)x1-x2.解得x0=4kAB=4.即得kAB=1ꎬ从而y0=4+m.由垂径定理ꎬ得ABʅMI.所以kAB kMI=-1.即1 4+m-114+1/2=-1ꎬ解得m=52.联立y=x+52与x2=8yꎬ消去yꎬ得x2-8x-20=0.从而|AB|=k2+1 |x1-x2|=k2+1(x1+x2)2-4x1x2=12+1 82-4ˑ(-20)=122.评注㊀抛物线中点差法的结论x0k=p 体现了相交弦中点横坐标与弦所在直线斜率的等量关系.本题中ꎬ求直线l方程中m的值是关键.点差法与垂径定理的联合ꎬ将问题转化为点的坐标运算ꎬ从而求出m的值.应注意ꎬ对于解答题ꎬ需写出点差法的推导过程ꎬ即先将弦的两端点坐标代入曲线方程中ꎬ作差后再利用平方差公式和中点坐标公式化为中点坐标与斜率的关系[1].例4㊀已知椭圆C:x216+y212=1ꎬ点A(-4ꎬ0)ꎬB(4ꎬ0)ꎬ点P和Q分别是椭圆C和圆M:x2+y2=16上不同于AꎬB的两点ꎬ设直线PBꎬQB的斜率分别为k1ꎬk2ꎬ且k1=34k2ꎬ求证:AꎬPꎬQ三点共线.解析㊀在椭圆C中ꎬ由椭圆第三定义ꎬ得kPB kPA=-b2a2.即k1 kPA=-34.又k1=34k2ꎬ所以34k2 kPA=-34ꎬ得kPA=-1k2.在圆M中ꎬ由kQA kQB=-1ꎬ即kQA k2=-1ꎬ得kQA=-1k2.所以kPA=kQA.又直线PA与QA共点Aꎬ所以AꎬPꎬQ三点共线.评注㊀如果圆的弦经过该圆圆心ꎬ则称该弦为该圆的直径ꎬ类似地ꎬ椭圆的弦经过该椭圆的中心ꎬ则称该弦为该椭圆的直径.本题中ꎬ线段AB是椭圆的直径ꎬ通过椭圆第三定义得到椭圆上一点与另两点连线的两斜率之积.如果把圆看作是特殊的椭圆ꎬ那么在圆中 kQB kQA=-1 可看作是椭圆中kPB kPA=-b2a2 的特殊情形ꎬ由这两组斜率关系和条件中的斜率关系推出的新的斜率关系ꎬ恰好达到证明的目的.例5㊀在平面直角坐标系xOy中ꎬ已知直线l:3x+y+m=0与双曲线C:x2a2-y2b2=1(a>0ꎬb>0)的右支交于MꎬN两点(点M在第一象限).若点Q满足OMң+OQң=0ꎬ且øMNQ=30ʎꎬ则双曲线C的渐近线方程为.解析㊀由3x+y+m=0ꎬ得l的斜率为-3ꎬ故l的倾斜角为120ʎ.又øMNQ=30ʎꎬ所以直线QN的倾斜角为120ʎ+30ʎ=150ʎꎬ如图10.图10㊀例5解析图由OMң+OQң=0知ꎬO为线段MQ的中点.由双曲线第三定义得kMN kQN=b2a2.即b2a2=-3 tan150ʎ=1ꎬ即ba=1.所以双曲线C的渐近线方程为y=ʃx.评注㊀本题由双曲线第三定义快速得到关于aꎬb的齐次分式与kMNꎬkQN的等量关系ꎬ再由直线MN的倾斜角及条件中的已知角求得kQNꎬ从而得到关于aꎬb的齐次方程ꎬ即得双曲线的渐近线方程.利用双曲线第三定义解题ꎬ首先要寻找过双曲线中心的相交弦ꎬ其次在双曲线上另找一点ꎬ向弦两端点引直线ꎬ再将这两直线的斜率转化为可求的量.参考文献:[1]任栋.圆锥曲线第三定义及点差法的应用[J].中学数学ꎬ2019(15):48-49.[责任编辑:李㊀璟]。
大招14第三定义与点差法 大招总结圆锥曲线第三定义: 平面内动点到两定点()1,0A a - 和 ()2,0A a 的斜率乘积等于常数 2e 1- 的点的轨 迹为植圆或双曲线. 其中两定点为椭圆或双曲线的顶点. 当 20e 1<< 时为椭圆, 当 2e 1> 时为双曲线.在椭圆 2222:1(0)x y C a b a b +=>> 中, A B 、 是关于原点对称的两点, P 是椭圆上异于 A B 、 的一点, 若 PA PB k k 、 存在,则有: 222e 1PA PB b k k a⋅=-=-在双曲线 2222:1x y C a b-= 中, A B 、 是关于原点对称的两点, P 是双曲线上异于A B 、 的一点, 若 PA PB k k 、 存在, 则有 222:e 1PA PBb k k a⋅=-=抛物线结论: 已知直线 l 与抛物线相交于 ,A B 两点, 点 M 为 AB 的中点, O为原点,则 0AB p k y =证明: 已知 PB 是椭圆 22221(0)x y a b a b+=>> 一条弦, M 是 PB 的中点, O为椭圆的中心. 若 PB OM k k 、 存 在, 先证明: 22PB OMb k k a⋅=-证明 : 设()()1122,,,P x y B x y 且 12x x ≠,则 ()2211221,1x y a b+=,()2222221,2x y a b +=()() 1?2- 得: 2222121222x x y y a b --=-,()()2121221212.b x x y y x x a y y +-∴=--+,()()2121221212PB b x x y y k x x a y y +-∴==--+ 又 1212OMy y k x x +=+,221,PB OMb k a k ∴=-⋅ 22PB OM b k k a ∴⋅=- 此方法称之为点差法, 设点作差, 设而不求.再证明第三定义, 延长 BO 交椭圆于 ,A PAB 的PA边所对的中位线,PA MO MO k k =, 由点差法结论: 222e 1MO PBb k k a ⋅=-=- 知 222e 1PA PB b k k a⋅=-=- 成立.双曲线第三定义的证明: 只需将椭圆中的 2b 全部换成 2b - 即可 抛物线结论证明: 设()()1122,,,A x y B x y , 抛物线方程 22y px =2211222,2y px y px ==()()()1212122y y y y p x x +-=-()()1212022y y p p x x y y -==-垂径定理如图,已知直线l 与椭圆相交于 ,A B 两点,点M 为AB 的中点,O 为原点,则如图,已知直线l 与双曲线相交于,A B 两点,点M 为AB 的中点,O为原点,则22.OM ABb k k a=-22.OM ABb k k a=(注:直线l 与双曲线的渐近线相交于,A B 两点,其他条件不变,结论依然成立)如图,已知点,A B 椭圆长轴端点(短轴端 点),P 是椭圆上异于,A B 的一点,则22PA PBb k k a=-.推广:如图,已知点,A B 是椭圆上关于原点 对称的两点,P 是椭圆上异于,A B 的一点,若直线,PA PB 的斜率存在且不为零,22PA PBb k k a=-如图,已知点,A B 双曲线实轴端点,P 是双曲线上异于,A B 的一点,则22PA PBb k k a=.推广:如图,已知点,A B 是双曲线上关于原点对称的两点,P 是双曲线上异于,A B 的一点,若直线,PA PB 的斜率存在且不为零,则22PA PBb k k a=.【中点弦·思维引导1】已知AB 是圆221x y +=的一条弦,点P 是AB 中点,当AB 和OP 斜率存在时.思考:OP AB k k ⋅是否为定值?解:点P 是AB 中点,所以AB OP ⊥(垂径定理),所以1OP AB k k ⋅=-.【中点弦・思维引导2】已知AB 是椭圆2214x y +=的一条弦,点P 是AB 中点,当AB 和OP 斜率存在时.思考:OP AB k k ⋅是否为定值?解:设()()1122,,,A x y B x y ,则1212,22x x y y P ++⎛⎫⎪⎝⎭.点A 和点B 在椭圆上,则有221122221414x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩作差得:()()()()12121212104x x x x y y y y +-++-= 所以()()()()1212121214y y y y x x x x +-=-+-,即14OP ABk k =-.(此方法名为“点差法”,即设点+作差)【第三定义推广·思维引导1】已知AB 是圆221x y +=的直径,点P 是圆上一点,当PA PB 、斜率存在时.思考:PA PB k k ⋅是否为定值?解:AB 是直径,所以PA PB ⊥,所以1PA PB k k ⋅=-.【第三定义推广・思维引导2】1.已知A B 、是椭圆22143x y +=上关于原点对称的两点,点P 是椭圆上一点.当PA PB 、斜率存在时,思考:PA PB k k ⋅是否为定值?解:设()()1122,,,A x y P x y ,取AP 中点G ,则1212,22x x y y G ++⎛⎫⎪⎝⎭. 点A 和点P 在椭圆上,则有22112222143143x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩作差得:()()()()1212121211043x x x x y y y y +-++-=所以()()()()1212121234y y y y x x x x +-=-+-,即34OG AP k k ⋅=-.点O 和G 分别是AB 和AP 的中点,所以//OG PB ,所以34PA PB k k ⋅=-.2.已知A B 、在椭圆22221(0)y x a b a b+=>>上,点P 是AB 的中点,当AB 和OP 斜率存在时.求证:AB OP k k ⋅为定值.解:设()()1122,,,A x y B x y ,则1212,22x x y y P ++⎛⎫⎪⎝⎭.点A 和点B 在椭圆上,则有22112222222211y x a b y x a b ⎧+=⎪⎪⎨⎪+=⎪⎩作差得()()()()1212121222110y y y y x x x x a b +-++-= 所以()()()()2121221212y y y y a x x x x b+-=-+-,即22OP AB a k k b =-.3.已知A B 、在双曲线22221(0,0)x y a b a b-=>>上,点P 是AB 的中点,当AB 和OP斜率存在时.求证:AB OP k k ⋅为定值.解:设()()1122,,,A x y B x y ,则1212,22x x y y P ++⎛⎫⎪⎝⎭. 2211222222221 ,? 1x y a b A B x y a b ⎧-=⎪⎪⎨⎪-=⎪⎩点和点在双曲线上则有 ()()()()()()()()121212122222121222121211,? .OP AB x x x x y y y y a by y y y b b k k x x x x a a +--+-=+-==+-作差得所以即4.已知A B 、在双曲线22221(0,0)y x a b a b-=>>上,点P 是AB 的中点,当AB 和OP 斜率存在时.求证:AB OP k k ⋅为定值. 解:设()()1122,,,A x y B x y ,则1212,22x x y y P ++⎛⎫⎪⎝⎭.2211222222221 ,? 1y x a b A B y x a b ⎧-=⎪⎪⎨⎪-=⎪⎩点和点在双曲线上则有 作差得()()()()1212121222110y y y y x x x x a b+--+-= ()()()()221212221212 ,? .?OP AB y y y y a a k k x x x x b b +-==+-所以即5.已知A B 、在抛物线22(0)y px p =>上,点P 是AB 的中点,当AB 斜率存在时,求证:AB P k y ⋅为定值.解:设()()1122,,,A x y B x y ,则1212,22x x y y P ++⎛⎫⎪⎝⎭.点A 和点B 在拋物线上,则有21122222y px y px ⎧=⎨=⎩作差得()()()1212122y y y y p x x +-=-所以1212122y y y y p x x -+⋅=-,即P AB y k p ⋅=.6.已知A B 、在抛物线22(0)x py p =>上,点P 是AB 的中点,当AB 不与y 轴垂直时,求证:PABx k 为定值. 解:设()()1122,,,A x y B x y ,则1212,22x x y y P ++⎛⎫⎪⎝⎭.点A 和点B 在抛物线上,则有21122222x py x py ⎧=⎨=⎩作差得()()()1212122x x x x p y y +-=-1212122 ,? .?P AB x x xp p y y k x x +==--所以即7.已知A B 、是椭圆22221(0,0)x y a b a b+=>>上关于原点对称的两个点,点P 在椭圆上.当PA 和PB 斜率存在时,求证:PA PB k k ⋅为定值.解:设()()1122,,,P x y A x y ,则()1212221212,,,PA PB y y y y B x y k k x x x x -+--==-+点A 和点P 在椭圆上,则有22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩作差得()()()()1212121222110x x x x y y y y a b +-++-=所以2121221212y y y y b x x x x a-+⋅=--+,即22PA PBb k k a=-.8.已知A B 、是椭圆22221(0,0)y x a b a b+=>>上关于原点对称的两个点,点P 在椭圆上.当PA PB 、斜率存在时,求证:PA PB k k ⋅为定值.解:设()()1122,,,P x y A x y ,则()1212221212,,,PA PB y y y y B x y k k x x x x -+--==-+点A 和点P 在椭圆上,则有22112222222211y x a by x a b ⎧+=⎪⎪⎨⎪+=⎪⎩作差得()()()()1212121222110y y y y x x x x a b +-++-=所以2121221212y y y y a x x x x b-+⋅=--+,即22PA PBa k k b=-.9.已知A B 、是双曲线22221(0,0)x y a b a b-=>>上关于原点对称的两个点,点P 在双曲线上.当PA 和PB 斜率存在时,求证:PA PB k k ⋅为定值. 解:设()()1122,,,P x y A x y ,则()1212221212,,,PA PB y y y y B x y k k x x x x -+--==-+点A 和点P 在双曲线上,则有22112222222211x y a b x y a b ⎧-=⎪⎪⎨⎪-=⎪⎩作差得()()()()1212121222110x x x x y y y y a b +--+-=所以2121221212y y y y b x x x x a -+⋅=-+,即22PA PBb k k a=. 10.已知A B 、是双曲线22221(0,0)y x a b a b-=>>上关于原点对称的两个点,点P 在双曲线上.当PA PB 、斜率存在时,求证:PA PB k k ⋅为定值.解:设()()1122,,,P x y A x y ,则()1212221212,,,PA PB y y y y B x y k k x x x x -+--==-+点A 和点P 在椭圆上,则有22112222222211y x a by x a b ⎧-=⎪⎪⎨⎪-=⎪⎩作差得()()()()1212121222110y y y y x x x x a b+--+-= 所以2121221212y y y y a x x x x b-+⋅=-+,即22PA PB a k k b =.典型例题例1.椭圆22:143x y C +=的左、右顶点分别为12,A A ,点P 在C 上且直线2PA 的斜率的取值范围是[-2,1]-,那么直线1PA 斜率的取值范围是A .1,12⎡⎤⎢⎥⎣⎦ B .3,14⎡⎤⎢⎥⎣⎦ C .13,24⎡⎤⎢⎥⎣⎦ D . 33,84⎡⎤⎢⎥⎣⎦解:由椭圆的标准方程可知,左右顶点分别为()()122,02,0A A -、, 设点()(),2P a b a ≠±,则22143a b += (1),12,22P P b bk k a a ==+-; 则1222224P PA b b b k k a a a ⋅=⋅=+--, 将(1)式代入得12PA PA 34k k ⋅=-, []2PA 2,1k ∈--,133,84P k ⎡⎤∴∈⎢⎥⎣⎦.故选D .例2.已知A B 、是椭圆22221(0)x y a b a b+=>>长轴的两个端点,,M N 是椭圆上关于x轴对称的两点,直线,AM BN 的斜率分别为12,k k ,且120k k ≠.若12k k +的最小值为1,则椭圆的离心率 A .12B.2 C.2 D.3解:设()()()()0000,,,,,0,,0M x y N x y A a B a --001200,y y k k x a a x ==+-0001200021y y y k k x a a x x a +=+==+-+ 当且仅当0000y y x a a x =+-,即000,x y b ==时等号成立 212ba b a∴==∴=又因为222a b c c =+∴=2c e a ∴== 故选C .例3.已知A B 、分别为椭圆2221(03)9x y b b +=<<的左、右顶点,P Q 、是椭圆上的不同两点且关于x 轴对称,设直线AP BQ 、的斜率分别为,m n ,若点A 到直线y =的距离为1,则该椭圆的离心率为A .12 B .4 C .13D .2解:由椭圆2221(03)9x y b b +=<<,得()()3,0,3,0A B -, 设()00,P x y ,则()00,Q x y -,2200219x y b ∴+=,则2202099y b x -=-. 0000,33AP BQ y y m k n k x x -====+-, 2202099y b mn x -∴==-.∴直线y =化为y x ==30y -=.由点A 到直线y =的距离为1,1=,解得2638b =, 22298c a b ∴=-=,则4c =.则4c e a ==. 故选B .例4.已知双曲线22112x y -=,过()1,1B 能否作直线l ,使l 与双曲线交于,P Q 两点,且 B 是线段PQ 的中点,这样的直线如果存在,求出它的方程;如果不存在,说明理由.解:假设这样的直线存在,设,P Q 的坐标分别为()()1122,,,x y x y ,则12122,2x x y y +=+=,又21x ()()222122111,11,222y x y -=-= (1)-(2)得:()()()()12121212102x x x x y y y y +--+-=, ()()121220x x y y ∴---=PQ ∴的斜率 12122y y k x x -==-又直线l 过,,P Q B 三点,l ∴的方程为()121y x -=-,即21y x =-.但若将21y x =-代入22112x y -=整理得方程22430x x -+=,而此方程无实数解,所以满足题设的直线不存在.例5.已知椭圆2212x y +=,求斜率为2的平行弦中点的轨迹方程. 解:设弦的两个端点分别为()()1122,,,,P x y Q x y PQ 的中点为(),M x y .则()()222212121,11,222x x y y +=+= (1)-(2)得:()()22221212121212120,022x x x x y y y y y y x x -+-+-=∴++=-.又121212122,2,2,40y y x x x y y y x y x x -+=+==∴+=-.弦中点轨迹在已知椭圆内,∴所求弦中点的轨迹方程为40x y +=(在已知椭圆内).例6.直线():50l ax y a --+=(a 是参数)与抛物线2:(1)f y x =+的相交弦是AB ,则弦AB 的中点轨迹方程是________.解:设()()1122,,,A x y B x y AB 、中点(),M x y ,则122x x x +=.()():150,l a x y l --+=∴过定点()51,5,1AB MN y N k k x +-∴==-. 又()()()()2211221,11,2y x y x =+=+(1)-(2)得:()()()()2212121212112y y x x x x x x -=+-+=-++,1212122AB y y k x x x x -∴==++-.于是5221y x x +=+-,即227y x =-. 弦中点轨迹在已知拋物线内,∴所求弦中点的轨迹方程为227y x =-(在已知拋物线内).例7.(2021·陕西咸阳市·高三一模(理))已知双曲线2222:1(0,0)x y C a b a b -=>>上存在两点,A B 关于直线6y x =-对称,且线段AB 的中点坐标为()2,4M -,则双曲线C 的离心率为A B C .2 D 解:方法1:设()()1122,,,A x y B x y , 且线段AB 的中点坐标为()2,4M -,则12124,8x x y y +=+=-,又,A B 关于直线6y x =-对称,所以121211y y x x -⨯=--,且,A B 在双曲线上,2222112222221,1x y x y a b a b-=-=, 相减可得22221212220x x y y a b---=,即()()()()12121212220x x x x y y y y a b +-+--=, 故22480a b-=,即222b a =,离心率为e ==故选B .方法2:直接用结论,由于,A B 关于直线6y x =-对称,即221,1AB AB OMb k k k a=-⋅=⇒-⨯2240220b a --==-即离心率为e ==B .例8.(2021·西藏昌都市第一高级中学高三期末(文))已知椭圆()2222:1(0),2,1x y M a b D a b+=>>是椭圆M 的一条弦AB 的中点,点()4,1P -在直线AB 上,求椭圆M 的离心率A .3 B . 23 C . 12D .2 解:方法1:设()()1122,,,A x y B x y 则22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩两式相减可得()()()()1212121222x x x x y y y y a b -+-++=故()()()()1212121222x x x x y y y y a b -+-+=-()()()()()12122212121x x y y a y y b x x +-=-+-()2,1D 是椭圆M 的一条弦AB 的中点故12124,2x x y y +=+=,代入(1)式中可得2122124111224AB y y b k a x x -+-⋅====--- 故有()222222a b a c ==-则a =,则2c a = 故选D 方法2:直接用结论,由于,,,A B P M 四点共线,即11101,42202AB PM AB ODk k k k ---=⋅=⋅=---.22221122b b a a -=-⇒=即离心率为2e ==,故选D 例9.(2021·河南驻马店市高三期末(文))已知双曲线2222:1(0,0)x y C a b a b-=>>的离心率为32,直线l 与C 交于,A B 两点,若线段AB 的中点为()4,3P ,则直线l 的方程为 A .53290x y +-= B .53110x y --= C .3530x y -+= D .35280x y +-=解:方法1:设()()1122,,,A x y B x y ,则2222112222221,1x y x y a b a b-=-=,两式相减可得()()12122x x x x a -+()()12122y y y y b -+-=.因为线段AB 以点()4,3P 为中点,所以12128,6x x y y +=+=,所以22121222121243y y x x b b x x y y a a-+=⋅=-+,因为C 的离心率为32,所以2222514b c a a =-=,故直线l 的斜率为53,所以直线l 的方程为()5343y x -=-,即53110x y --=,经检验成立. 故选B方法2:直接用结论,32e ==即222253055,44043AB OP AB AB b b k k k k a a -=⋅=⋅==⇒=-,所以直线l 的方程为()5343y x -=-,即53110x y --=,经检验成立.故选B例10.(2021·江苏苏州市·高三期末)已知双曲线2222:1(0,0)y x C a b a b-=>>的上、下顶点分别为1A ,2A ,点P 在双曲线C 上(异于顶点),直线12,PA PA 的斜率乘积为34,则双曲线C 的渐近线方程为 A .12y x =±B.2y x =±C.3y x =±D .2y x =±解:方法1:设点()00,p x y ,又()()120,,0,A a A a -,则120000,PA PA y a y ak k x x -+==所以1222000200034PA PA y a y a y a k k x x x -+-⋅=⋅==,又因为点P 在双曲线C 上得2200221y x a b -=,所以2220022y a x a b -=,故222022034y a a x b -==,所以2a b = 则双曲线C的渐近线方程为a y x x b =±=. 故选B方法2:直接用结论122234PA PA a k k b ⋅==,所以a b =则双曲线C 的渐近线方程为ay x b=±=x ± 故选B例 11.(2021•贵州贵阳市·高三期末(理))过抛物线24y x =的焦点的直线与抛物线交于,A B 两点,若AB 的中点的纵坐标为2,则AB 等于A .4B .6C .8D .10解:方法1:拋物线24y x =的焦点坐标()1,0F ,准线方程:1l x =-,设AB 的中点为M ,过,,A B M 作准线l 的垂线,垂足分别为,,C D N ,则MN 为梯形ABDC 的中位线,AB AF BF AC BD ∴=+=+ ()0221MN x ==+∣,直线AB 过拋物线的焦点,F ∴可设直线AB 的方程为:1(x my m =+为常数),代入拋物线的方程消去x 并整理得:2440y my --=,设,A B 的纵坐标分别为12,y y ,线段AB 中点()00,M x y ,则12022,12y y y m m +===∴=, ∴直线AB 的方程为001,1213x y x y =+∴=+=+=,()2318AB ∴=+=,故选C .方法2 :直接用结论21tan 2AB o p k y α====即222445,8sin 2p ABαα====⎛ ⎝⎭.故选C例12.(2021•上海杨浦区•复旦附中高二期末)已知三角形ABC 的三个顶点都在椭圆:22143x y +=上,设它的三条边,,AB BC AC 的中点分别为,,D E M ,且三条边所在线的斜率分别为123,,k k k ,且123,,k k k 均不为0.O 为坐标原点,若直线,,OD OE OM 的斜率之和为1.则()123111k k k ++= A .43-B .3-C .1813- D .32- 解:方法1:设()()()()()()112233112233,,,,,,,,,,,A x y B x y C x y D s t E s t M s t ,因为,A B 在椭圆上,所以2211143x y +=,2222143x y +=, 两式相减得:121211121213344y y x x sk x x y y t -+==-⨯=-⨯-+,即111413t k s =-, 同理可得3222334411,33t t k s k s =-=-, 所以31212312311143t t tk k k s s s ⎛⎫++=-++ ⎪⎝⎭因为直线OD OE OM 、、的料率之和为1,所以12311144133k k k ++=-⨯=-, 故选A .方法2:直接用结论2123234OD OE OMb k k k k k k a ⋅=⋅=⋅=-=-,所以1314OD OE OM k k k k ⎛++=- ⎝ 23111k k ⎫++=⎪⎭即12311144133k k k ++=-⨯=-.故选A例13.(2021·福建龙岩市·高二期末)过点()1,1P 的直线l 与双曲线2212y x -=交于,M N 两点,且点P 恰好是线段MN 的中点,则直线l 的方程为________. 解:方法1:过点()1,1P 的直线l 与该双曲线交于,M N 两点,设()()1122,,,M x y N x y ,2211222212,12y x y x ⎧-=⎪⎪∴⎨⎪-=⎪⎩, 两式相减可得:()()()()1212121212x x x x y y y y -+=+-, 因为P 为MN 的中点,12122,2x x y y ∴+=+=,()12122x x y y ∴-=-,则12122MN y y k x x -==-,所以直线l 的方程为()121y x -=-,即为210x y --=.故答案为:210x y --=.方法2:直接用结论2210210l OP l a k k k b -⋅=⇒⋅=-得2l k =,点斜式得答案()121y x -=-即2x -10y -=.例14.(2021·河南高三月考(文))已知双曲线22221(0,0)x y a b a b -=>>,斜率为12的直线l交双曲线于,M N O 、为坐标原点,P 为MN 的中点,若OP 的斜率为2,则双曲线的离心率为ABC.D .4解:方法1:设点()()1122,,M x y N x y 、,则1212,22x x y y P ++⎛⎫⎪⎝⎭,由题意,得2222112222221,1x y x y a b a b -=-=,两式相减,得22222121220x x y y a b ---=,整理得2222122221y y b x x a-=-, 所以122222121222122121212OP MNy y y y y y b k k x x x x x x a +--⋅=⋅===+--, 因此,双曲线的离心率为c e a =====故选A.方法2:用结论一步到位2222122l OP b b k k a a ⋅=⇒⨯=得e ==故选A.例15.(2020-天津高考真题)已知椭圆22221(0)x y a b a b+=>>的一个顶点为()0,3A -,右焦点为F ,且,OA OF O =∣为坐标原点.(1)求椭圆方程;(2)已知点C 满足3OC OF =,点B 在椭圆上(B 异于椭圆的定点),直线AB 与以C 为圆心的圆相切于点P ,且P 为线段AB 的中点,求直线AB 的方程.解(I)棛圆22221(0)x y a b a b+=>>的一个顶点为()0,3A -,3b ∴=,由OA OF =,得3c b ==,又由222a b c =+,得2223318a =+=,所以,椭圆的方程为221189x y +=; 方法1:(II)直线AB 与以C 为圆心的圆相切于点P ,所以CP AB ⊥, 根据题意可知,直线AB 和直线CP 的斜率均存在,设直线AB 的斜率为k ,则直线AB 的方程为3y kx +=,即3y kx =-,2231189y kx x y =-⎧⎪⎨+=⎪⎩,消去y ,可得()2221120k x kx +-=,解得0x =或21221k x k =+. 将21221k x k =+代入3y kx =-,得222126332121k k y k k k -=⋅-=++,所以,点B 的坐标为2221263,2121k k k k ⎛⎫- ⎪++⎝⎭,因为P 为线段AB 的中点,点A 的坐标为()0,3-,所以点P 的坐标为2263,2121k k k -⎛⎫ ⎪++⎝⎭,由3OC OF =,得点C 的坐标为()1,0,所以,直线CP 的斜率为222303216261121CPk k k k k k --+==-+-+,又因为CP AB ⊥,所以231261k k k ⋅=--+,整理得22310k k -+=,解得12k =或1k =.所以,直线AB 的方程为132y x =-或3y x =-. 方法2:(II)直线AB 与以C 为圆心的圆相切于点P ,所以CP AB ⊥,根据题意可知,直线AB 和直线CP 的斜率均存在,设直线AB 的斜率为k ,则直线AB 的方程为3y kx =-,设AB 直线为()113,,y kx P x y =-,点差法结论(注意写出证明过程)易得121211211211619212,318321OP ABk y x k y b k x k k k a x y y kx k ⎧⎧=⎪⎪⋅=-⎪⎪+⋅=-⇒⋅=-⇒⇒⎨⎨-⎪⎪==-⎪⎪+⎩⎩,所以点P 的坐标为2263,2121kk k -⎛⎫ ⎪++⎝⎭,由3OC OF =,得点C 的坐标为()1,0,所以,直线CP 的斜率为222303216261121CPk k kk k k --+==-+-+,又因为CP AB ⊥,所以231261k k k ⋅=--+,整理得22310k k -+=,解得12k =或1k =.所以,直线AB 的方程为132y x =-或3y x =-.例16.[2018-全国卷高考真题(理)]斜率为k 的直线l 交椭圆22143x y +=于A B 、两点,线段AB 的中点为()1,(0),M m m F >是椭圆右焦点.(1)证明:12k <-.(2)点P 是椭圆上一点且0FP FA FB ++=,证明,,FA FP FB 成等差,并求出公差.解 (1)标准点差法例题(注意先证明结论,在此直接写出重点)22330144AB OMb m k k k m a k⋅=-⇒⋅=-⇒=->,即0k <且()1,?M m 必在椭圆内221143m +<⇒2314143k ⎛⎫- ⎪⎝⎭+<解得12k >或12k <-又0k <,故12k <-. (2)由题意得()1,0F ,设()33,P x y ,则()()()()3311221,1,1,0,0x y x y x y -+-+-=. 由(1)及题设得()()31231231,20x x x y y y m =-+==-+=-<.又点P 在C 上,所以34m =,从而331,,22P FP ⎛⎫-= ⎪⎝⎭.于是(122xFA x ===-.同理222x FB =-. 所以()121432FA FB x x +=-+=. 故2FP FA FB =+,即,,FA FP FB 成等差数列. 设该数列的公差为d ,则12122d FB FA x x =-=-=由34m =得1k =-. 所以l 的方程为74y x =-+,代入C 的方程,并整理得2171404x x -+=.故121212,28x x x x +==,代入(2)解得28d =.所以该数列的公差为28或28-.例17.(2014-江西卷)过点()1,1M 作斜率为12-的直线与椭圆2222:1(0)x y C a b a b+=>>相交于,A B ,若M 是线段AB 的中点,则椭圆C 的离心率为_________.解 方法1:设()()1122,,,A x y B x y ,则()()22221122222211,12x y x y a b a b+=+=,M 是线段AB 的中点,12121,1,22x x y y ++∴==直线AB 的方程是()1112y x =--+,()12121,2y y x x ∴-=--过点()1,1M 作斜率为12-的直线与椭圆2222:1x y C a b +=(0)a b >>相交于,A B 两点,M 是线段AB 的中点,∴(1)(2)两式相减可得22221212220x x y y a b --+=,即2221202c a c b e a b a ⎛⎫+-⋅=∴=∴=∴== ⎪⎝⎭. 方法2:直接用结论2222110210AB OMb b k k a a -⋅=-⇒-⨯=--则2212b a =即离心率为e =2=自我检测1.已知中心在原点,一焦点为(F 的椭圆被直线:32l y x =-截得的弦的中点的横坐标为12,求椭圆的方程.解:设椭圆的方程为22221y x a b+=,则2250a b -=(1)设弦端点()()1122,,P x y Q x y 、,弦PQ 的中点()00,M x y ,则00012012011,3221,2122x y x x x x y y y ==-=-+==+==-又2222112222221,1y x y x a b a b+=+= 两式相减得()()()()22121212120b y y y y a x x x x +-++-= ()()221212-0b y y a x x -+-=即()22122212,32y y a a x x b b-==-联立(1)(2)解得2275,25a b ==所求椭圆的方程是2217525y x +=2.已知椭圆22143x y +=,试确定m 的取值范围,使得对于直线4y x m =+,椭圆上总有不同的两点关于该直线对称.解:设()()111222,,,P x y P x y 为椭圆上关于直线4y x m =+的对称两点,(),P x y 为弦12P P 的中点,则,222211223412,3412x y x y +=+=两式相减得,()()22221212340x x y y -+-= 即()()()()12121212340x x x x y y y y +-++-=1212121212,2,4y y x x x y y y x x -+=+==--3y x ∴=这就是弦12P P 中点P 轨迹方程. 它与直线4y x m =+的交点必须在椭圆内联立34y x y x m =⎧⎨=+⎩,得3x my m =-⎧⎨=-⎩则必须满足22334y x <-,即()223334m m <-,解得m <<3.若抛物线2:C y x =上存在不同的两点关于直线():3l y m x =-对称,求实数m 的取值范围.解:当0m =时,显然满足.当0m ≠时,设抛物线C 上关于直线():3l y m x =-对称的两点分别为()()1122,,P x y Q x y 、,且PQ 的中点为()00,M x y ,则()()221122,1,2y x y x ==(1)-(2)得:22121212PQ 1212011,2y y y y x x k x x y y y --=-∴===-+, 又01,2PQ m k y m =-∴=-. 中点()00,M x y 在直线():3l y m x =-上,()003y m x ∴=-,于是052x =. 中点在抛物线2y x =区域内200M y x ∴<,即2522m ⎛⎫-< ⎪⎝⎭,解得m <<综上可知,所求实数m 的取值范围是(4.双曲线2222:1(0,0)x y E a b a b-=>>被斜率为4的直线截得的弦AB 的中点为()2,1,则双曲线E 的离心率为( )方法1:设()()1122,,,A x y B x y 代入双曲线方程作差有:()()()()1112121222x x x x y y y y ab-+-+=,有()()()()21212212122y y y y b a x x x x -+==-+,所以223,c e a==故选B.方法2:设AB 中点为P 用结论一步到位22104220AB OPb k k a -⋅=⨯==-得e ==故选B.5.(2021-湖北武汉市-高考模拟(文))过点()4,2P 作一直线AB 与双曲线22:12x C y -=相交于A 、B 两点,若P 为AB 中点,则AB =( )A. B. D.方法1:易知直线AB 不与y 轴平行,设其方程为()24y k x -=-代入双曲线22:12x C y -=,整理得()()222128213232100k x k k x k k -+--+-=设此方程两实根为12,x x ,则()12282121k k x x k -+=-又()4,2P 为AB 的中点, 所以()2821821k k k -=-,解得1k =当1k =时,直线与双曲线相交,即上述二次方程的0∆>, 所求直线AB 的方程为24y x -=-化成一般式为121220.8,10,x y x x x x AB --=+===12x x -==.故选D.方法2:设AB 中点为P 用结论一步到位22201402AB OPAB b k k k a -⋅=⋅==-得1AB k =.即直线:AB y x =-2,与双曲线联立得2128100,x x AB x -+==-==.故选D.6.(2013-北京)已知,,A B C 是椭圆22:14x W y +=上的三个点,O 是坐标原点.(I)当点B 是W 的右顶点,且四边形OABC 为菱形时,求此菱形的面积; (II)当点B 不是W 的顶点时,判断四边形OABC 是否可能为菱形,并说明理由. 解:()I 四边形OABC 为菱形,B 是椭圆的右顶点()2,0∴直线AC 是BO 的垂直平分线,可得AC 方程为1x =设()1,A t ,得22114t +=,解之得2t =(舍负)A ∴的坐标为1,2⎛⎫ ⎪ ⎪⎝⎭,同理可得C 的坐标为1,2⎛- ⎝⎭因此AC =可得菱形OABC 的面积为12S AC BO =⋅=(II)方法1:四边形OABC 为菱形,OA OC ∴=, 设()1OA OC r r ==>,得A C 、两点是圆222x y r +=与椭圆22:14x W y +=的公共点,解之得22314x r =- 设A C 、两点横坐标分别为12x x 、,可得A C 、两点的横坐标满足12x x ==,或1x =2x =,(1)当123x x ==时,可得若四边形OABC 为菱形,则B 点必定是右顶点()2,0;(2)若13x =23x =-则120x x +=, 可得AC 的中点必定是原点O ,因此A O C 、、共线,可得不存在满足条件的菱形OABC 综上所述,可得当点B 不是W 的顶点时,四边形OABC 不可能为菱形.方法2:直接利用结论22114OM AB b k k a =-=-≠-,结束战斗!7.已知椭圆22221(0)x y a b a b+=>>,过右焦点()23,0F 的直线交椭圆于A B 、,且()1,1M -是线段AB 的中点,1F 是椭圆左焦点,求1F AB 的面积.解析:易知直线13:22AB y x =-,由椭圆第三定义可知 ()22222221010113102AB OMAB MF b b b k k k k a a a ----⋅=-=⇒⋅=-⇒=--,且22183,9a cb ⎧==⇒⎨=⎩,联立直线AB 与椭圆方程为2221216129018923x y y y y y x y ⎧+=⎪⇒+-=⇒-==⎨⎪=+⎩1121211622F ABS F F y y =⋅-=⨯=8.抛物线24y x =,过点(2,0)的直线AC 和BD 相互垂直(斜率均存在),M N 、分别是AC 和BD 的中点.求证:直线MN 过定点.方法1:由题意可得,这两条直线的斜率均存在,且不为0,设()()1:2,:2AC y k x BD y x k=-=--,由抛物线第三定义可知()222222222222, ,1212222222,2M M MN N N k y p k M y k k k k k k k y p k y k N k k k k ⎧⎧⎧⎛⎫⋅==⎪--⎪⎪+=⇒ ⎪⎪⎪⎪⎝⎭⇒⇒⇒==⎨⎨⎨-⎛⎫-⋅==⎪⎪⎪+-+=-+- ⎪⎪⎪⎪⎝⎭⎩⎩⎩分刟代人直线 故直线MN 方程为()()()222222411k k y k x k y x k k--=--⇒=---,故直线MN 过定点()4,0方法2:由题意可得,这两条直线的斜率均存在,且不为0, 设()()1:2,:2AC y k x BD y x k=-=--,由抛物线第三定义可知()2222222,,12222,2M MN N k y p M y k k k y p y k N k k k ⎧⎧⎪⎪⎛⎫⋅==⎪⎪+= ⎪⎪⎪⎝⎭⇒⇒⎨⎨⎪⎪⎪⎪-⋅===-+-⎪⎪⎩⎩分别代入直线 令222222k k+=+得21k =, 此时2222224k k+=+=,故直线MN 过点()4,0H , 当21k ≠时,22222020,22241124NH MH k k kkk k k k k k---====+---+-. 所以,,,NH MH k k M H N =三点共线,所以直线MN 过定点()4,0H .9.双曲线221169x y -=,过点()5,0P 的直线AB 和CD 相互垂直(斜率存在),M N 、分别是AB 和CD 的中点. 求证:直线MN 过定点.方法1:设AB 直线为()()115,,y k x M x y =-,点差法结论(注意写出证明过程)易得()212121121111280991691616455169OM ABk y x k y b k x k k k a x ky k x y k ⎧⎧=⎪⎪⋅=⎪⎪-⋅=⇒⋅=⇒⇒⎨⎨⎪⎪=-=⎪⎪-⎩⎩,所以2228045,169169k k M k k ⎛⎫⎪--⎝⎭(1)当0k =时,M 点即是P 点,此时,直线MN 为x 轴.(2)当0k ≠时,将上式M 点坐标中的k 换成1k -,同理可得228045,169169k N k k -⎛⎫ ⎪--⎝⎭. (1)当直线MN 不垂直于x 轴时,直线MN 的斜率()222222454571691698080161169169MN k kk k k k k kk k +--==----, 其方程()22245780169169161k k y x k k k -⎛⎫-=- ⎪---⎝⎭,化简得()27807161k y x k ⎛⎫=- ⎪-⎝⎭,所以直线MN 过定点80,07⎛⎫⎪⎝⎭;(2)当直线MN 垂直于x 轴时,2228080169169k k k =--,此时,1k =±,直线MN 也过定点80,07⎛⎫ ⎪⎝⎭.综上所述,直线MN 过定点80,07⎛⎫⎪⎝⎭.方法2:设AB 直线为()()115,,y k x M x y =-,点差法结论(注意写出证明过程)易得()212121121111280991691616455169OM ABk y x k y b k x k k k a x ky k x y k ⎧⎧=⎪⎪⋅=⎪⎪-⋅=⇒⋅=⇒⇒⎨⎨⎪⎪=-=⎪⎪-⎩⎩,所以2228045,169169k k M k k ⎛⎫⎪--⎝⎭(1)当0k =时,M 点即是P 点,此时,直线MN 为x 轴.(2)当0k ≠时,将上式M 点坐标中的k 换成1k -,同理可得228045,169169k N k k -⎛⎫ ⎪--⎝⎭. 令2228080169169k k k =--得21k =,设MN 过定点H 此时2228080801691697k k k ==--,故直线MN 过点80,07H ⎛⎫⎪⎝⎭, 当21k ≠时,()()222222245450077169169,8080808016116116971697MHNHk kk k k k k k k k k k k -----====------. 所以,,,NH MH k k M H N =三点共线,所以直线MN 过定点80,07H ⎛⎫⎪⎝⎭. 10.椭圆22143x y +=,过点()1,0F 的直线AB 和CD 相互垂直(斜率存在),M N 、分别是AB 和CD 的中点.求证:直线MN 过定点.方法1:设AB 直线为()()111,,y k x M x y =-,点差法结论(注意写出证明过程)易得()212121121111243334443134OM ABk y x k y b k x k k k a x ky k x y k ⎧⎧=⎪⎪⋅=-⎪⎪+⋅=-⇒⋅=-⇒⇒⎨⎨-⎪⎪=-=⎪⎪+⎩⎩,所以22243,3434k k M k k ⎛⎫- ⎪++⎝⎭(1)当0k =时,M 点即是F 点,此时,直线MN 为x 轴.(2)当0k ≠时,将上式M 点坐标中的k 换成1k -,同理可得2243,3434k N k k ⎛⎫ ⎪++⎝⎭.(1)当直线MN 不垂直于x 轴时,直线MN 的斜率()222222337343444413434MN k kk k k k k k k k --++==--++, 其方程()2222374343441k k k y x k k k ⎛⎫--=- ⎪++-⎝⎭,化简得()274741k y x k ⎛⎫=- ⎪-⎝⎭,所以直线MN 过定点4,07⎛⎫⎪⎝⎭;(2)当直线MN 垂直于x 轴时,222443434k k k =++,此时,1k =±,直线MN 也过定点4,07⎛⎫ ⎪⎝⎭.综上所述,直线MN 过定点4,07⎛⎫⎪⎝⎭.方法2:设AB 直线为()()111,,y k x M x y =-,点差法结论(注意写出证明过程)易得()2121211211112ˆ34334443134OM ABk y x k y b k x k k k a x ky k x y k ⎧⎧=⎪⎪⋅=-⎪⎪+⋅=-⇒⋅=-⇒⇒⎨⎨-⎪⎪=-=⎪⎪+⎩⎩,所以22243,3434k k M k k ⎛⎫- ⎪++⎝⎭(1)当0k =时,M 点即是F 点,此时,直线MN 为x 轴.(2)当0k ≠时,将上式M 点坐标中的k 换成1k -,同理可得2243,3434k N k k ⎛⎫ ⎪++⎝⎭.令222443434k k k =++得21k =,设MN 过定点H . 此时22244434347k k k ==++,故直线MN 过点4,07⎛⎫⎪⎝⎭, 当21k ≠时,22222223300773434,44444444347347MHNH k kk kk k k k k k k k k -----++====----++.所以,,,NH MH k k M H N =三点共线,所以直线MN 过定点4,07⎛⎫⎪⎝⎭.。
高考数学圆锥曲线重要结论一、定义:第一定义:平面内到两定点F1(-c,0),F2(c,0)的距离和为定值(大于两定点间的距离|F1F2|)2a的点的轨迹叫椭圆,两定点叫椭圆的焦点,两焦点间的距离叫焦距,与坐标轴的交点叫顶点。
第二定义:平面内到一个定点F的距离与到定直线1的距离比为常数e(0<e<1)的点的轨迹,定点叫椭圆的焦点,定直线叫椭圆的准线;引申定义:⒈若一个圆C1内含于另一个圆C2,则与大圆内切与小圆外切的圆的圆心的轨迹为一椭圆,两圆的圆心为焦点,其长轴长为两圆半径之和;⒉在一个圆内有一点,则过该点且与已知圆相切的圆的圆心的点的轨迹为一椭圆,且其长轴长为已知圆的半径。
⒊过两点的两条直线的斜率之积为一负常数m的点的轨迹为一椭圆(两点除外)。
两定点为椭圆的顶点,两定点间的距离为长轴长。
(-1<m<0时,焦点在x轴上;当m<-1时,焦点在y轴上)例:过点(-8,0),(8,0)的两直线11,12的斜率之积为-3/8,求其交点的轨迹。
⒋将圆的横坐标(或纵坐标)拉伸或缩短为原来的m倍,该圆变成椭圆;⒌连接圆内一定点与圆上任一点的线段的垂直平分线与圆上该点到圆心的连线的交点的轨迹为一椭圆。
方椭圆的长半轴与圆的半径长相等;⒍两个同心圆较大圆上任一点与圆心的连线与小圆交于一点,从大圆上该点作x轴的垂线,则过小圆交点向该垂线作垂线,其垂足的点的轨迹为椭圆。
对应练习:⑴在椭圆上任一点M与焦点F1F2构成△MF1F2,I为该三角形的内心,连MI交长轴于N点,则MI/IN的值为多少?⑤若过点P作∠F1PF2的平分线交过点F1作其平分线的垂线于M,交PF2于N点,则有PF1=PN,所以有⑶在椭圆上任一点P求:·的最大值(a2-c2),PF1×PF2的最大值a2,点P到对应顶点的最短距离为a-c.⑷若在椭圆内部有一点M,要求作一点P使该点到右焦点F的距离与到该定点的距离和最小。
高中数学解析几何圆锥曲线的第三定义与斜率乘积是定值模型问题探究 问题与知识提出: 圆锥曲线的第三定义:平面内的动点到两定点1,0A a 2,0A a 的斜率乘积等于常数21e 点的轨迹叫做椭圆或双曲线,其中两个定点为椭圆和双曲线的两个顶点.其中如果常数211e时,轨迹为双曲线,如果211,0e 时,轨迹为椭圆。
圆锥曲线的第三定义的有关结论:1.椭圆方程中有关22b a-的经典结论(1).AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM ABb k k a⋅=-.(2).椭圆的方程为22221x y a b+=(a >b >0),,A A 为椭圆的长轴顶点,P 点是椭圆上异于长轴顶点的任一点,则有1222PA PA b K K a=-(3). 椭圆的方程为22221x y a b+=(a >b >0),,B B 为椭圆的短轴顶点,P 点是椭圆上异于短轴顶点的任一点,则有1222PB PB b K K a=-(4). 椭圆的方程为22221x y a b+=(a >b >0),过原点的直线交椭圆于,A B 两点,P 点是椭圆上异于,A B 两点的任一点,则有22PA PBb K K a=-2.双曲线方程中有关22b a的经典结论(1)AB 是双曲线22221x y a b -=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM ABb k k a⋅=, 即2020ABb x K a y =。
(2)双曲线的方程为22221x y a b-=(a >0,b >0),,A A 为双曲线的实轴顶点,P 点是双曲线上异于实轴顶点的任一点,则有1222PA PA b K K a= (3)双曲线的方程为22221x y a b-=(a >0,b >0),,B B 为双曲线的虚轴端点,P 点是双曲线上异于虚轴端点的任一点,则有1222PB PB b K K a= (4) 双曲线的方程为22221x y a b-=(a >0,b >0),过原点的直线交双曲线于,A B 两点,P点是双曲线上异于,A B 两点的任一点,则有22PA PB b K K a= 典型例题:例1.(2019全国卷2理科数学第21题)已知点A (−2,0),B (2,0),动点M (x ,y )满足直线AM与BM 的斜率 之积为−12.记M 的轨迹为曲线C .(1)求C 的方程,并说明C 是什么曲线;(2)过坐标原点的直线交C 于P ,Q 两点,点P 在第一象限,PE ⊥x 轴,垂足为E ,连结QE 并延长交C 于点G .(i )证明:PQG △是直角三角形; (ii )求PQG △面积的最大值.例2.已知平行四边形ABCD 内接于椭圆()2222:10x y a b a bΩ+=>>,且AB , AD 斜率之积的范围为32,43⎛⎫-- ⎪⎝⎭,则椭圆Ω离心率的取值范围是( )A. 12⎛ ⎝⎭B. ⎝⎭C. 14⎛ ⎝⎭D. 11,43⎛⎫⎪⎝⎭例3.设椭圆()012222>>=+b a by a x C :的左右顶点为A,B.P 是椭圆上不同于A,B 的一点,设直线AP,BP 的斜率分别为m,n ,则当()||ln ||ln 32323n m mnmn b a +++⎪⎭⎫ ⎝⎛-取得最小值时,椭圆C 的离心率为( )A.51B.22C.54D.23例4.已知椭圆()2222:10x y C a b a b+=>>的左,右焦点分别为1F ,2F ,12F F =,经过点1F 的直线(不与x 轴重合)与椭圆C 相交于A ,B 两点,△2ABF 的周长为8. (1)求椭圆C 的方程;(2)经过椭圆C 上的一点Q 作斜率为1k ,2k (10k ≠,20k ≠)的两条直线分别与椭圆C 相交于异于点Q 的M ,N 两点.若M ,N 关于坐标原点对称,求12k k 的值巩固提升:1.已知椭圆C : 22221(0)x y a b a b+=>>的长轴长为4, A , B 是其长轴顶点, M 是椭圆上异于A , B 的动点,且34MA MB k k ⋅=-.(1)求椭圆C 的标准方程;(2)如图,若动点R 在直线6x =上,直线AR , BR 分别交椭圆C 于P , Q 两点.请问:直线PQ 是否过定点?若是,求出定点坐标;若不是,请说明理由.2.如图,设点,A B 的坐标分别为()),,直线,AP BP 相交于点P ,且它们的斜率之积为23-. (1)求点P 的轨迹方程;(2)设点P 的轨迹为C ,点M N 、是轨迹为C 上不同于,A B 的两点,且满足//,//AP OM BP ON ,求证:MON ∆的面积为定值.3.已知椭圆C:22 221(0)x ya ba b+=>>的短轴长为25,离心率为32,圆E的圆心在椭圆C上,半径为2,直线1y k x=与直线2y k x=为圆E的两条切线.(1)求椭圆C的标准方程;(2)试问:12*k k是否为定值?若是,求出该值;若不是,说明理由.4.如图,在平面直角坐标系xOy中,椭圆2222:1x yCa b+=(0)a b>>的离心率为12,右准线的方程为4,x=1,F2F分别为椭圆C的左、右焦点,A,B分别为椭圆C的左、右顶点.(1)求椭圆C的标准方程;(2)过(,0)T t()t a>作斜率为k(0)k<的直线l交椭圆C于M,N两点(点M在点N的左侧),且12//F M F N,设直线AM,BN的斜率分别为1,k2k,求12k k⋅的值.5.已知椭圆C :()222210x y a b a b +=>>()2,1M 在椭圆上,O 为坐标原点.(1)求椭圆C 的标准方程;(2)已知A 、B 为椭圆上不同的两点.①设线段AB 的中点为点T ,证明:直线AB 、OT 的斜率之积为定值;②若A 、B 两点满足()0OA OB OM λλ+=≠,当OAB ∆的面积最大时,求λ的值.6.已知椭圆E :,直线l 不过原点O 且不平行于坐标轴,l 与E 有两个交点A ,B ,线段AB 的中点为M .若,点K 在椭圆E 上,、分别为椭圆的两个焦点,求的范围; 证明:直线OM 的斜率与l 的斜率的乘积为定值;若l 过点,射线OM 与椭圆E 交于点P ,四边形OAPB 能否为平行四边形?若能,求此时直线l 斜率;若不能,说明理由.2229(0)x y m m +=>()13m =1F 2F 12KF KF ⋅()2()3,3mm ⎛⎫ ⎪⎝⎭高中数学解析几何圆锥曲线的第三定义与斜率乘积是定值模型问题探究 问题与知识提出: 圆锥曲线的第三定义:平面内的动点到两定点1,0A a 2,0A a 的斜率乘积等于常数21e 点的轨迹叫做椭圆或双曲线,其中两个定点为椭圆和双曲线的两个顶点.其中如果常数211e时,轨迹为双曲线,如果211,0e 时,轨迹为椭圆。
圆锥曲线的三定义圆锥曲线的第三定义及运用一、 椭圆和双曲线的第三定义1. 椭圆在椭圆()2222C 10x y aba b+=:中,A 、B 是关于原点对称的两点,P 是椭圆上异于A、B的一点,若PA PB k k 、存在,则有:222=1=PA PB b k k e a •-- 证明:构造△PAB 的PA 边所对的中位线MO ,PA MO k k =,由点差法结论:222=1=MO PB b k k e a •--知此结论成立。
2. 双曲线在双曲线2222C 1x y a b -=:中,A 、B是关于原点对称的两点,P 是椭圆上异于A、B的一点,若PA PB k k 、存在,则有:222=1=PA PB b k k e a •-证明:只需将椭圆中的2b 全部换成2b -就能将椭圆结论转换成双曲线的结论。
二、 与角度有关的问题例题一:已知椭圆()2222C 10x y aba b+=:的离心率2e =,A 、B是椭圆的左右顶点,为椭圆与双曲线22178x y -=的一个交点,令PAB=APB=αβ∠∠,,则()cos =cos 2βαβ+ ...解答:令=PBx γ∠,由椭圆第三定义可知:21tan tan =1=4e αγ•--()()()cos cos cos cos sin sin 1tan tan 3===cos 2cos cos cos sin sin 1tan tan 5γαβγαγααγαβγαγαγααγ-++•=+++-•点评:其实所谓的双曲线方程只是一个障眼法,并不影响题目的解答。
两顶点一动点的模型要很快的联想到第三定义,那么剩下的任务就是把题目中的角转化为两直线的倾斜角,把正余弦转化为正切。
题目中的正余弦化正切是三角函数的常见考点☆。
..变式1—1:(石室中学2015级高二下4月18日周末作业)已知双曲线22C 2015x y -=:的左右顶点分别为A 、B ,P 为双曲线右支一点,且=4PAB APB ∠∠,求=PAB ∠ .解答:令=02PAB πα⎡⎤∠∈⎢⎥⎣⎦,,=02PBA πβ⎡⎤∠∈⎢⎥⎣⎦,,则=5βα,由双曲线的第三定义知: 2tan tan =tan tan5=1=1e αβαα••-则:1tan ==tan 5=5=tan52212πππαααααα⎛⎫-⇒-⇒ ⎪⎝⎭点评:与例题1采取同样的思路转化角,但对于正切转换的要求较高。
圆锥曲线的第三定义及运用一、 椭圆和双曲线的第三定义1. 椭圆在椭圆()2222C 10x y a b a b +=f f :中,A 、B 是关于原点对称的两点,P 是椭圆上异于A 、B 的一点,若PA PB k k 、存在,则有:222=1=PA PB b k k e a•--证明:构造△PAB 的PA 边所对的中位线MO ,PA MO k k =,由点差法结论:222=1=MO PB b k k e a•--知此结论成立。
2. 双曲线在双曲线2222C 1x y a b -=:中,A 、B 是关于原点对称的两点,P 是椭圆上异于A 、B 的一点,若PA PBk k 、存在,则有:222=1=PA PB b k k e a •-证明:只需将椭圆中的2b 全部换成2b -就能将椭圆结论转换成双曲线的结论。
二、 与角度有关的问题例题一:已知椭圆()2222C 10x y a b a b+=f f :的离心率2e =,A 、B 是椭圆的左右顶点,为椭圆与双曲线22178x y -=的一个交点,令PAB=APB=αβ∠∠,,则()cos =cos 2βαβ+.解答:令=PBx γ∠,由椭圆第三定义可知:21tan tan =1=4e αγ•--()()()cos cos cos cos sin sin 1tan tan 3===cos 2cos cos cos sin sin 1tan tan 5γαβγαγααγαβγαγαγααγ-++•=+++-•点评:其实所谓的双曲线方程只是一个障眼法,并不影响题目的解答。
两顶点一动点的模型要很快的联想到第三定义,那么剩下的任务就是把题目中的角转化为两直线的倾斜角,把正余弦转化为正切。
题目中的正余弦化正切是三角函数的常见考点☆。
变式1-1:(石室中学2015级高二下4月18日周末作业)已知双曲线22C 2015x y -=:的左右顶点分别为A 、B ,P 为双曲线右支一点,且=4PAB APB ∠∠,求=PAB ∠.解答:令=02PAB πα⎡⎤∠∈⎢⎥⎣⎦,,=02PBA πβ⎡⎤∠∈⎢⎥⎣⎦,,则=5βα,由双曲线的第三定义知:2tan tan =tan tan5=1=1e αβαα••-则:1tan ==tan 5=5=tan52212πππαααααα⎛⎫-⇒-⇒ ⎪⎝⎭点评:与例题1采取同样的思路转化角,但对于正切转换的要求较高。
两锐角正切乘积为1即表示sin α=cos β,cos α=sin β⇒两角互余☆,则可解出α的值。
当然双曲线的题目较于椭圆和抛物线题目考试概率较小,但既然提到了双曲线的第三定义,不妨做一做。
三、 与均值定理有关的问题例题2:已知A 、B 是椭圆()222210x y a b a b+=f f 长轴的两个端点,M 、N 是椭圆上关于x 轴对称的两点,直线AM 、BN 的斜率分别为12k k 、,且120k k ≠。
若12k k +的最小值为1,则椭圆的离心率为.解答一(第三定义+均值):由题意可作图如下:连接MB ,由椭圆的第三定义可知:222=1=AMBM b k k e a •--,而BM BN k k =-⇒2122=b k k a∴1221=1==22b b k k e a a +≥⇒⇒解答二(特殊值法):这道题由于表达式()12min1k k +=非常对称,则可直接猜特殊点求解。
121==2k k 时可取最值,则M 、N 分别为短轴的两端点。
此时:121====22b k k e a ⇒。
点评:对于常规解法,合理利用M 、N 的对称关系是解题的关键,这样可以利用椭圆的第三定义将两者斜率的关系联系起来,既构造了“一正”,又构造了“二定”,利用均值定理“三相等”即可用a 、b 表示出最值1。
当然将12k k 、前的系数改为不相等的两个数,就不能利用特殊值法猜答案了,但常规解法相同,即变式2-1。
变式2-1:已知A 、B 是椭圆()222210x y a b a b+=f f 长轴的两个端点,M 、N 是椭圆上关于x 轴对称的两点,直线AM 、BN 的斜率分别为12k k 、,且120k k ≠12+的最小值为1,则椭圆的离心率为.解答:连接MB,由椭圆的第三定义可知:222=1=AM BMbk k ea•--,而BM BNk k=-⇒2122=bk ka∴1241=1=4b bea a+≥⇒⇒变式2-2:已知A、B是椭圆()222210x ya ba b+=f f长轴的两个端点,若椭圆上存在Q,使23AQBπ∠=,则椭圆的离心率的取值围为.解答一(正切+均值):令Q在x轴上方,则直线QA的倾斜角为02πα⎡⎤∈⎢⎥⎣⎦,,直线QB的倾斜角为2πβπ⎡⎤∈⎢⎥⎣⎦,。
2AQBππ⎡⎤∠∈⎢⎥⎣⎦,,()tan tantan tan1tan tanAQBβαβαβα-∠=-=+由椭圆的第三定义:22tan tan=baαβ-,则22tan=tanbaβα-带入可得:22222222tantan tantan tan tan==1tan tan11bbaab ba aαααβααβα⎛⎫-+⎪---⎝⎭+--2222222=11babab a ba a--≤---(取等条件:tanbaα=,即Q为上顶点)而tanx在2ππ⎡⎤⎢⎥⎣⎦,单增,则Q为上顶点时()maxAQB∠,所以此时23AQBπ∠≥,故1e⎫∈⎪⎪⎣⎭解答二(极限法):当Q趋近于A、B两点时,2AQBπ∠→(此时Q点所在的椭圆弧趋近于以AB为直径的圆的圆弧,AQB ∠相当于直径所对的圆周角);当Q 在A 、B 间运动时2AQB π∠f (Q 在以AB 为直径的圆部,AQB ∠f 直径所对的圆周角=90°),由椭圆的对称性可猜测当Q 为短轴端点时()max AQB ∠。
由于:椭圆上存在Q ,使23AQB π∠=,那么 Q 为短轴端点时()max 23AQB π∠≥。
取临界情况,即Q 为短轴端点时23AQB π∠=,此时3a e b ==;当椭圆趋于饱满(0e →)时,椭圆趋近于圆,圆的直径所对的圆周角永远为90°,不满足;当椭圆趋于线段(1e →)时,()maxAQB π∠→,满足。
故1e ⎫∈⎪⎪⎣⎭。
当然这些只需要在头脑中一想而过,简洁而有逻辑。
点评:这道题可以增加对于圆周角的理解,在用极限法讨论:“当Q 趋近于A 、B 两点时,2AQB π∠→”时能会颠覆“AQB π∠→”的认知,当然这肯定是错的,结合常规解法可以看出此时是角最小的情况,而不是角最大的情况。
要搞清楚,不然会被弄晕的。
对于常规解法选择正切表示角的大小的原因有二:①与第三定义发生联系②tanx 在2ππ⎡⎤⎢⎥⎣⎦,单增便于利用tanx 的大小比较角度的大小。
四、 总结归纳1. 上述部分题目的常规解法较复杂,但做题时一定要能猜答案,而且要猜得有理由。
2. 对于均值不等式,注意取等条件是“三相等”,即相等时取最值。
这可以帮助猜测表达形式是高度对称的式子的最值,如:例题23. 极限法可以刻画出单调变化的某一变量的端点值,如:变式2-2中P 在椭圆上滑动,角度的变化一定是光滑的(无突变,连续), 所以只需考虑边界值。
4. 做几何的选填题时,有时利用圆周角定理可以很快的找到最大角,注意学会恰当运用,如:变式2-2。
5. 常以正切值刻画角度大小。
6. 在做综合性较大的题目时要联系各种知识,灵活转化,以最巧妙的方法致胜。
7. .8..五、 方法针对上文提到的“圆周角找最大角”与“椭圆中另一类均值”进行拓展补充,各附例题。
例题3:在平面直角坐标系XOY 中,给定两点()1,2M - 和()1,4N ,点P 在X 轴上移动,当MPN ∠取最大值时,点P 的横坐标为.解答一(正切+均值):已知:()1,2M - 、()1,4N ,:3MN l y x =+与x 轴交于()03,0P - 令(),0P t ,则:21MP k t =--,41NP k t=-,=MPN θ∠ ① 当3t =-时,=0θ② 当3t -f 时,MP l 的倾斜角较大,226tan ==17MP NP MP NP k k t k k t θ-++•+令30x t =+f ,则222622tan ===1676166t x t x x x x θ+≤+-++-(tan 0θf ) 此时4x =,1t =,max 4πθ=③ 当3t -p 时,NP l 的倾斜角较大,226tan ==17NP MP MP NP k k t k k t θ-+-+•+()30x t =-+f,则2226221tan ===16761676t x t x x x x θ+-≤+++++ (tan 0θf )此时4x =,7t =-,()max 1tan 7θ=由于[)0θπ∈,,且tan θ在[)0θπ∈,上单增,[]tan 01θ∈,max 4πθ∴=,此时1t =解答二(圆周角定理):本题中的取极值时的P 点的几何意义为:过M 、N 的圆与x 轴切于P 点。
下面给出证明:证明:以与x 轴切于2P 点的圆满足所求最大角为例:由于3MN l y x =+:是过M 、N 两点的圆的一条弦,由垂径定理知圆心在3l y x =-+:上 随着圆心横坐标从0开始增大:当半径r 较小时,圆与x轴无交点;当半径稍大一点时,圆与x 轴相切,有一个交点;当半径更大一点时,圆与x 轴有两交点3P 、4P 。
此时:根据圆周角定理:342Q =MP N MP N M N MP N ∠=∠∠∠p ,可知:圆与x 轴相切时,()max MPN ∠。
R 较小的情况(圆与x 轴相离) R 较大的情况(圆与x 轴相交于3P 、4P )所以:过M 、N 的圆与x 轴切于3P 、4P 点时,分别有()max MPN ∠⇒只需比较1MPN ∠与2MP N ∠,哪一个更大。
令与x 轴相切的圆的圆心为(),x y ,则切点(),0P x ,半径为y圆满足:()()()()2222222126707114x y y x x x or x y y⎧++-=⎪⇒-+=⇒=-⎨-+-=⎪⎩ (消去y )比较可知:当x=1时,()max MPN ∠点评:常规方法依旧是利用正切度量角的大小,但注意用倾斜角表示所求角时要用大角减去小角,才能得到正角;均值时要注意以分子(一次)为新元构建均值。
用圆周角角的性质解答,只要转化为切点,解一个方程组,比较两个角谁大就行了。
(不比较也行,画图可知右边角大于左边角:弦长相等,半径越大,弦所对的圆周角越小。
)其实两种解法的难度是一样,只是一种要写得多,一种要想得多。
☆变式3-1:若G 为△ABC 的重心,且AG BG ⊥,则sin C 的最大值为.解答一(余弦定理+均值):令()0,0G ,(),0A a ,()0,b B ,则由()()()13,13G A B CG A B Cx x x x C a b y y y y ⎧=++⎪⎪⇒--⎨⎪=++⎪⎩由点间的距离公式:AB =AC =BC =由余弦定理:22222222244cos 2a b a b a b AC BC AB C AC BC +++-++-=⨯⨯222242a b a b++()22522a ba b +≤⇒≤+ ()max 433cos 0sin sin 555C C C ∴≥⇔≤≤⇔= 解法二(圆周角定理):令()1,0A -,()1,0B ,()G sin ,cos θθ,则()C 3sin ,3cos θθ题目转化为:()1,0A -,()1,0B ,()C ,x y 满足:229x y +=,求sin C 的最大值。