当前位置：文档之家 › 五多重共线性分布滞后模型或机动

五多重共线性分布滞后模型或机动

  • 格式：pdf
  • 大小：724.23 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

分布滞后模型

分布滞后模型

2019/4/16
Y * t 0 1 X t t （6.3.12）
由于存在滞后现象，Yt 的实际变化（Yt—Yt-1） 只是预期变化（Y*t-1—Yt-1）的一部分，需要按预定 水平逐步进行调整，从而作出如下调整假设：
Yt Yt 1 Y * t Yt 1 （6.3.13）
式中，
t t 1 t 1
（6.3.9）
18
2019/4/16

由以上讨论可知，根据几何分布滞后模型 的假定，我们可以把无限分布滞后模型变 换为仅包含3个参数的自回归模型（见 （6.3.9））。
19
2019/4/16
（二）部分调整模型
该模型早先用来研究物资储备问题，亦称存 货调整模型。 例如，本期商品的库存量的期望值（最佳库 存量）取决于本期实际销售额。 因此，作如下的理论假设：被解释变量的希 望值（最佳值）Y*t是Xt的线性函数 20
3
2019/4/16
0 ：称为短期影响乘数，它表示解释变量 X 变化一个单位
对同期被解释变量 Y 产生的影响。
1 , 2 ,... ：称为延期影响乘数，因为它们是测度以前不同时期
X 变化一个单位对 Y 的滞后影响。

i
0 1 3 ... ，称为长期影响乘数，表示
二、产生滞后模型的原因
（一）心理因素 收入、GDP、 （二）技术因素 货币发行与通货膨胀、投入与产出 （三）制度因素 改造家用电器的功能、款式与厂商的利润 6
2019/4/16
三、分布滞后模型估计的问题
对分布滞后模型直接采用最小二乘法估计参数时会 遇到如下困难： 1、无法估计无限分布滞后模型； 2、没有先验准则预先确定最大滞后长度k； 3、若滞后期较长而样本较小时，将缺乏足够的自由 度进行估计和检验； 4、解释变量存在序列相关，带来多重共线性的问题。

分布滞后模型

分布滞后模型

S.E. of regression
21.88962 Akaike info criterion
Sum squared resid
7187.333 Schwarz criterion
Log likelihood
-75.52028 F-statistic
Durbin-Watson stat
1.438436 Prob(F-statistic)
8.2 有限分布滞后模型及其估计
如果有限分布滞后模型
yt a b0 xt b1xt1 ...... bk xtk ut
中的参数bi（i＝0，1，2，…，k）的分布可以 近似地用一个关于i的低阶多项式表示，就可以利 用多项式减少模型中的参数。
8.2 有限分布滞后模型及其估计
8.2 有限分布滞后模型及其估计
8.2.2 有限分布滞后模型的估计方法 1．经验加权估计法 根据实际经济问题的特点及经验判断，对滞后 变量赋予一定的权数，利用这些权数构成各滞后变 量的线性组合，以形成新的变量，再应用最小二乘 法进行估计。
8.2 有限分布滞后模型及其估计
基本思路是设法减少模型中被估计的参数个数。 模型中参数的个数主要由解释变量的个数来决定， 要减少模型中被估计的参数个数，就要对解释变量 进行归并，并通过解释变量的归并，消除或削弱多 重共线性问题。
Prob. 0.0023 0.0000 818.6959 279.9181 9.120033 9.218058 2601.407 0.000000
8.2 有限分布滞后模型及其估计
Dependent Variable: Y
Method: Least Squares
Sample(adjusted): 1958 1974

高级计量经济学之第5章分布滞后与动态模型

高级计量经济学之第5章分布滞后与动态模型

高级计量经济学之第5章分布滞后与动态模型第5章分布滞后与动态模型§5.1 分布滞后模型很多经济模型在回归方程中有滞后项，例如，因为修建桥和高速公路需要很多时间，所以公共投资对GDP 的影响有一个滞后期，而且这个影响可能会持续数年；研发新产品需要时间，而后把这个新产品投入生产也需要时间；在研究消费行为时，一个工资的变化可能影响好几期的消费。

在消费的恒久收入理论中，消费者会用若干期去决定真实可支配收入的变化是暂时的还是永久的。

例如，今年额外的咨询费收入明年是否还会继续？同样，真实可支配收入的滞后值会在回归方程中出现，是因为消费者在平滑其消费行为时十分重视他自身的终身收入。

一个人的终身收入可以用他过去和现在的收入来推测。

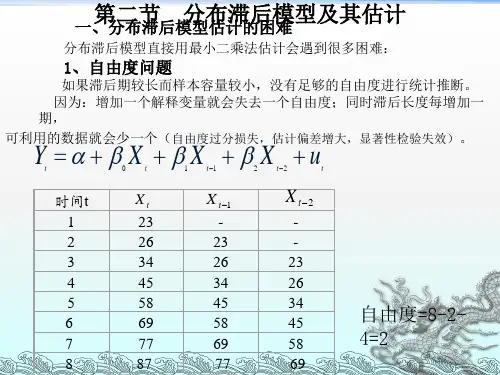
换句话说，回归关系可以写为：T t X X X Y ts t s t t t ,,2,1110 =+++++=--εβββα （5.1）其中，t Y 代表被解释变量Y 在第t 期的观测值，t s X -代表解释变量X 第t s -期的观测值，α为截距项，0β，1β，…，s β是t X 当期和滞后期的系数。

方程（5.1）式就是分布滞后模型因为它把收入增长对消费的影响分为s 期。

X 的一个单位变化对Y 的短期影响由0β来表示，而X 的一个单位变化对Y 的长期影响由(s βββ+++ 10)来表示。

假设我们观察从1955年到1995年的t X ，1t X -为相同的变量，但是提前一期的，也就是1954-1994。

因为1954年的数据观察不到，我们就从1955年开始观察1t X -，到1994年结束。

这意味着当我们滞后一期时，t X 序列将从1956年开始到1995年结束。

对于实际的应用来说，也就是当我们滞后一期时，我们将从样本中丢失了一个观测值。

所以如果我们滞后s 期，将丢失s 个观测值。

更进一步，对于每一个滞后值，都要估计出一个额外的β值。

因此，自由度会产生双重损失，即观测值数目的减少（因为引进滞后项），以及所需估计的参数增加。

计量经济学名词解释

计量经济学名词解释

1、截面数据：截面数据是许多不同的观察对象在同一时间点上的取值的统计数据集合，可理解为对一个随机变量重复抽样获得的数据。

2、时间序列数据：时间序列数据是同一观察对象在不同时间点上的取值的统计序列，可理解为随时间变化而生成的数据。

3、虚变量数据：虚拟变量数据是人为设定的虚拟变量的取值。

是表征政策、条件等影响研究对象的定性因素的人工变量，其取值一般只取“0”或“1”。

4、内生变量与外生变量：内生变量是由模型系统决定同时可能也对模型系统产生影响的变量，是具有某种概率分布的随机变量，外生变量是不由模型系统决定但对模型系统产生影响的变量，是确定性的变量。

5、总体回归函数：是指在给定X i 下Y 分布的总体均值与X i 所形成的函数关系（或者说将 总体被解释变量的条件期望表示为解释变量的某种函数）6、最大似然估计法（ML ）: 又叫最大或然法，指用产生该样本概率最大的原则去确定样本 回归函数的方法。

7、OLS 估计法：指根据使估计的剩余平方和最小的原则来确定样本回归函数的方法。

8、残差平方和：用RSS 表示，用以度量实际值与拟合值之间的差异，是由除解释变量之外 的其他因素引起的被解释变量变化的部分。

9、拟合优度检验：指检验模型对样本观测值的拟合程度，用2R 表示，该值越接近1表示拟合程度越好。

10、多元线性回归模型：在现实经济活动中往往存在一个变量受到其他多个变量影响的现象，表现在线性回归模型中有多个解释变量，这样的模型被称做多元线性回归模型，多元是指多个解释变量。

11、调整的可决系数：又叫调整的决定系数，是一个用于描述多个解释变量对被解释变量的联合影响程度的统计量，克服了2R 随解释变量的增加而增大的缺陷，与2R 的关系为2211(1)1n R R n k -=----。

12、偏回归系数：在多元回归模型中，每一个解释变量前的参数即为偏回归系数，它测度了当其他解释变量保持不变时，该变量增加1单位对被解释变量带来的平均影响程度。

分布滞后模型及其估计

分布滞后模型及其估计

将（2）代入（1），得
从而估计多项式的系数，再由多项式的系数与模型参数间
的
关系Yt，最 后 得0到X t分（布滞0 后 模1 型 。2）即X t1 （0 21 42）X t2 （0 31 92）X t3 ut
3
3
3
0 X ti 1 iX ti 2 i2 X ti ut (3)
权和Zt (各滞后变量的线性组合），把 Zt 作为新解释变量拟合一 元线性回归模型
Y Z u
t
0
1t
i
问题：不同时间的解释变量应该给多大的权数？
“经验加权法” 包括：
（1） 递减滞后结构
Xt
Xt-1
Xt-2
Xt-3
1/2
1/4
1/6
1/8
(令0 1 2 ) (令1 1 4 ) (令 2 1 6 ) (令 3 1 8 )
例 消费滞后模型
Yˆt 0.735 0.886Xt 0.012Xt1 0.010Xt2
t = （8.16）
（4.23）
（0.51）
（0.52）
R2 0.997
由于解释变量之间高度线性相关，由OLS估计的结果分析： 滞后收入对消费没有显著性影响（造成了一种假象）。
（三） 滞后长度难以确定 在大对数情况下，有限分布滞后模型的最大滞后长度S是未
j 1
例如 Yt 0 X t 1X t1 2 X t2 3 X t3 ut （1）
设 m 2 i 0 1i 2i2
(总约束）
i 0 0 0 1 0 2 0 0
i 1 1 0 1 2 i 2 2 0 21 42
(2)
(先验约束）
i 3 3 0 31 92
i0
i 1

计量经济学-中-4-分布滞后模型

计量经济学-中-4-分布滞后模型
在某时期的一个事件冲击后，从原来的均衡经过充分的调整达 到新的均衡之间的变化。
度的是以前不同时期Ｘ变化一个单位对Ｙ均值的滞后影响。
• 当然，分布滞后模型可以不仅含有两个 时间序列。这里主要是为了简化起见， 实际上，在有多个时间序列的情形，方 法是类似的。
二、滞后的原因
• 1. 归纳起来，产生滞后影响的原因有： 心理上的原因。作为一种习惯势力（或惰性）的结果，人 们在收入增加或价格上升后，并不马上改变他们的消费习 惯，甚至生活方式。
解决办法：
• 对于问题（3），一般通过引入被解释变量的滞后值 （AR项）作为解释变量，或引入随机误差项的滞后 值（MA项）来解决，即建立自回归分布滞后 （ADL：Auto-regressive Distributed Lag）模型：
Y
t
k Y Y Y X 1 t 1 2 t 2 p t p i 0 i t i
茨准则（Schwarz Criterion，简称为SC准则）来确
定适当的滞后长度k：
– 用这两个准则确定滞后长度k时，都要求使所计算的统计 量（AIC值或SC值）达到最小。 – 参见[美]乔治· 贾奇等《经济计量学理论与实践引论》 G·
P434。
对于无约束有限分布滞后模型，采用OLS
法估计所面临的特殊问题
达到最大的滞后长度 k；或者采用 AIC 准则或 SC 准 则，选择使 AIC 值或 SC 值达到最小的滞后长度 k ） 之外，还可以根据有关的经济理论确定。
确定多项式的次数p，可以按以下程序进行：先给p 一个较大的值（ 但p最大不得超过滞后长度k ），然
后用t检验逐步降低多项式的次数，直到模型中的所
2 i 0 1 2 p
p
（i=0，1，2，…，k） （3.4）

第五章 多重共线性(计量经济学-北京大学,岳昌君)

4
§2 多重共线性的来源
一、解释变量受同一因素的影响 时间序列数据： 1、经济发展;2、政治事件 3、偶然事件;4、时间趋势 二、解释变量中含有当期和滞后变量 I t 1 2 rt 3Yt 4Yt 1 ut Y2 Y3 Y1 , Yn ; Y n Y1 Y2 有多重共线性。 Yn 1
5
§3 多重共线性的影响
一、完全共线性 ˆ X Y ˆ无唯一解 ( X X ) ˆ 的方差是无穷大。 i
6
二、“不完全”多重共线性
ˆ的解不稳定。 ˆ 的方差非常大。 1、 i ˆ 2.8 ˆ 1 1 0.9 2 2 例如： 0.9 1 ˆ 2.9 ˆ 2 3 3 ˆ 2.8 ˆ 3.5678 0.99 1 2 2 0.99 ˆ ˆ 1 2 . 9 6 . 4322 3 3 ˆ 2.8 ˆ 40 .5743 0.999 1 2 2 0.999 2.9 ˆ ˆ 1 51 . 4257 3 3
观察结果（共线性诊断）：1、最大条件指数 37.1>30，说明中等相关；2、与最大条件指数在 一行的4个变量的方差比例都大于0.5，说明这4个 变量就是一个具有中等相关的变量集。
14
五、F检验
例如：X2，X3，X4相互回归
1、 X2—X3，X4；若F >F ，则有多重共线性； 否则的话，就没有。 2、 X3—X2，X4；若F >F ，则有多重共线性； 否则的话，就没有。
t 1 t t 1 t

回归模型中多重共线性的情形及其处理

丫= 1+ 8人-4人+ 3为=1 + 8人-（3X2+ 2）+ 3为=7+ 8人-9%（1.5）在（1.4）中，X2的系数为12,表示丫与为成正比例关系，即正相关；而在（1.5）中,X2的系数为-9,表示丫与X?成负比例关系，即负相关。

如此看来，同一个方程丫= 1+ 4片+ 3X2变换出的两个等价方程，由于不同的因式分解和替换，导致两个方程两种表面上矛盾的结果。

实际上，根据X1 = 3为+ 2式中的X1与为的共线性，X1约相当于3X2, 在（1.4）减少了3人，即需要用9个X2来补偿；而在（1.5）增加了4人, 需要用12个X2来抵消，以便保证两个方程的等价性，这样一来使得（1.5）中为的系数变为了负数。

从上述分析看来，由于X i与勺的共线性，使得同一个方程有不同的表达形式，从而使得丫与为间的关系难以用系数解释。

2•对多重线性关系的初步估计与识别如果在实际应用中产生了如下情况之一，则可能是由于多重共线性的存在而造成的，需作进一步的分析诊断。

①增加（或减去）一个变量或增加（或剔除）一个观察值，回归系数发生了较大变化。

②实际经验中认为重要的自变量的回归系数检验不显著。

③回归系数的正负号与理论研究或经验相反。

④在相关矩阵中，自变量的相关系数较大。

⑤自变量回归系数可信区间范围较广等。

3•对多重共线性本质的认识多重共线性可分为完全多重共线性和近似多重共线性（或称高度相关性），现在我们集中讨论多重共线性的本质问题。

多重共线性普遍被认为是数据问题或者说是一种样本现象。

我们认为，这种普遍认识不够全面，对多重共线性本质的认识，至少可从以下几方面解解。

（3）检验解释变量相互之间的样本相关系数。

假设我们有三个解释变量X i、X2、X3，分别以「12、「13、「23 来表示X i 与X2、X i 与X3、X2与X3之间的两两相关系数。

假设r i2 = 0.90,表明X i与X2之间高度共线性，现在我们来看相关系数「12,3，这样一个系数我们定义为偏相关系数，它是在变量X3为常数的情况下，X i与X2之间的相关系数。

第六章分布滞后模型与自回归模型分析

第六章分布滞后模型与自回归模型分析分布滞后模型（Distributed Lag Models）和自回归模型（Autoregressive Models）是常用于时间序列分析的两种方法。

本章将分别介绍这两种模型以及其在经济学和社会科学领域中的应用。

分布滞后模型是一种广义的线性回归模型，用于分析变量之间的滞后效应。

它的基本形式可以表示为：Yt = α + β1Xt + β2Xt-1 + ... + βpXt-p + et其中，Yt是被解释变量，Xt是解释变量，β1到βp是与解释变量相关的系数，et是误差项。

模型中的滞后项Xt-1到Xt-p表示X在当前时间以及过去的一段时间内对Y的影响。

分布滞后模型可以用来研究两个或多个变量之间的滞后效应，并帮助研究者了解这些变量之间的动态关系。

分布滞后模型在经济学和社会科学领域中有广泛的应用。

例如，在宏观经济学中，可以用分布滞后模型来研究货币政策对经济增长的长期影响。

在健康经济学中，可以用分布滞后模型来研究疫苗接种对流行病传播的影响。

在社会学研究中，可以用分布滞后模型来研究教育程度对就业机会的影响。

自回归模型是一种基于时间序列的统计模型，用于预测一个变量在时间上的变化。

它的基本形式可以表示为：Yt = α + φ1Yt-1 + φ2Yt-2 + ... + φpYt-p + et其中，Yt是被预测的变量，φ1到φp是自回归系数，et是误差项。

自回归模型假设当前时间的值与过去时间的值有关，并且根据过去时间的值来预测未来时间的值。

自回归模型可以帮助研究者预测变量的趋势和周期性，并提供关于未来值的信息。

自回归模型在经济学和社会科学领域中也有广泛的应用。

例如，在金融学中，可以用自回归模型来预测股票价格的变化。

在气象学中，可以用自回归模型来预测天气变化。

在市场研究中，可以用自回归模型来预测产品销售量。

总之，分布滞后模型和自回归模型是两种常用的时间序列分析方法。

它们可以帮助研究者了解变量之间的滞后效应和趋势，并用于预测未来值。

计量经济学期末考试名词解释

1. 总体回归函数：在给定解释变量X i 条件下被解释变量Y i 的期望轨迹称为总体回归线，或更一般地称为总体回归曲线。

相应的函数：E(Y 〡X i )=f(X i )称为（双变量）总体回归函数（populationregressionfunction,PRF ）2. 样本回归函数：样本散点图近似于一条直线，画一条直线以尽好地拟合该散点图，由于样本取自总体，可以该线近似地代表总体回归线。

该线称为样本回归线。

记样本回归线的函数形式为：i i i X X f Y 10ˆˆ)(ˆββ+==称为样本回归函数（sampleregressionfunction ，SRF ）。

3. 随机的总体回归函数：函数 〡 或者在线性假设下， 式称为总体回归函数（方程）PRF 的随机设定形式。

表明被解释变量除了受解释变量的系统性影响外，还受其他因素的随机性影响。

由于方程中引入了随机项，成为计量经济学模型，因此也称为总体回归模型。

4. 线性回归模型：假设1、回归模型是正确设定的。

假设2、解释变量X 是确定性变量，不是随机变量，在重复抽样中取固定值。

假设3、解释变量X 在所抽取的样本中具有变异性，而且随着样本容量的无限增加，解释变量X 的样本方差趋于一个非零的有限常数，即假设4、随机误差项具有零均值、同方差和不序列相关性：E(i )=0i=1,2,…,nVar(i )=2i=1,2,…,nCov(i,j )=0i≠ji,j=1,2,…,n假设5、随机误差项与解释变量X 之间不相关：Cov(X i ,i )=0i=1,2,…,n假设6、服从零均值、同方差、零协方差的正态分布i ~N(0,2)i=1,2,…,n以上假设也称为线性回归模型的经典假设，满足该假设的线性回归模型，也称为经典线性回归模型5. 随机误差项（ ）和残差项（ ）：（1）i 为观察值Y i 围绕它的期望值E(Y |X i )的离差，是一个不可观测的随机变量，又称为随机干扰项或随机误差项。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验五多重共线性、分布滞后模型（或机动）[实验目的]让学生掌握如何辨别模型中是否存在多重共线性现象，并能够对多重共线性加以处理。

[实验内容]①相关系数矩阵计算；②方差膨胀因子计算；③多重共线性处理。

[实验步骤]数据导入—查看t 统计量值和F 统计量值以及R 平方的值--计算相关系数矩阵和方差膨胀因子—对多重共线问题加以处理（改变模型、去除不重要的变量、岭回归主成分分析等）问题：对于1960年至1982年期间美国人均鸡肉消费量（Y），人均实际可支配收入（X1），鸡肉的实际零售价格（X2），猪肉的实际零售价格（X3），牛肉的实际零售价格（X4）等数据，见表4-1，利用它们的对数估计如下模型：表4-11960年至1982年期间美国人均鸡肉消费量等数据y x1x2x3x427.8397.542.250.778.329.9413.338.15279.229.8439.240.35479.230.8459.739.555.379.231.2492.937.354.777.433.3528.638.163.780.235.6560.339.369.880.436.4624.637.865.983.936.7666.438.464.585.538.4717.840.17093.740.4768.238.673.2106.140.3843.339.867.8104.841.8911.639.779.111440.4931.152.195.4124.140.71021.548.994.2127.640.11165.958.3123.5142.942.71349.657.9129.9143.644.11449.456.5117.6139.246.71575.563.7130.9165.550.61759.161.6129.8203.350.11994.258.9128219.651.72258.166.4141221.652.92478.770.4168.2232.6把数据导入GRETL 软件，产生各变量的对数变量，分别为ly、lx1、lx2、lx3、lx4，估计要求的模型，参数估计的结果为：εβββββ+++++=443322110ln ln ln ln ln X X X X Y图4-1模型估计的结果需求的收入弹性和需求的价格弹性都是高度显著的，但两个交叉弹性均不显著。

模型的决定系数为0.98，F统计量对应的P值很小，但lx3和lx4都不显著。

不过由此得出鸡肉的需求不受猪肉和牛肉价格的影响显然是不对的，模型中可能存在多重共线性问题。

为了诊断模型中是否存在共线性，首先来计算出自变量的相关矩阵，结果如下：图4-2自变量的相关矩阵相关系数都较大，说明可能存在共线性。

再计算各自变量的方差膨胀因子和自变量矩阵的矩阵条件数，GRETL软件会给出矩阵条件数的倒数。

Variance Inflation FactorsMinimum possible value=1.0Values>10.0may indicate a collinearity problemlx165.115lx217.486lx341.433lx442.307VIF(j)=1/(1-R(j)^2),where R(j)is the multiple correlation coefficientbetween variable j and the other independent variablesBelsley-Kuh-Welsch collinearity diagnostics:---variance proportions---lambda cond const lx1lx2lx3lx44.994 1.0000.0000.0000.0000.0000.0000.00531.9150.1950.0020.0000.0040.0020.000111.9180.1680.0620.2120.0560.0400.000136.9730.1770.0210.1080.2300.2100.000334.3720.4600.9140.6800.7100.748lambda=eigenvalues of X'X,largest to smallestcond=condition indexnote:variance proportions columns sum to 1.0图4-3共线性诊断结果几个变量对应的方差膨胀因子都挺大，一般大于10就表明存在模型中比较严重的共线性问题。

而且，自变量矩阵的条件数为334.372，一般认为矩阵条件数超过30就表明模型存在共线性问题。

这样，可以断定模型中存在多重共线性问题。

对于多重共线性的处理方法主要有：剔除P值大的自变量、增加样本容量、重新建模，此外还有主成分分析及岭回归等，我们这里只给出简单的处理办法，剔除不显著变量，结果如下图：图4-4共线性的处理结果和前面的回归结果比较，收入弹性增大了，但是价格弹性的绝对值却下降了。

不过需要注意的是，简化了的模型的系数估计是有偏的。

[实验方法]上机[实验条件]利用统计计量软件Gretl [实验指导]1.导入数据建立模型，根据模型结果判断是否存在多重共线性。

2.利用函数corr 计算相关系数矩阵。

3.Gretl 中能够直接判断共线性问题。

[问题思考]1.哪些现象反映模型中存在多重共线性？2.为什么根据方差膨胀因子能够判断是否存在多重共线性？3.为什么有时我们可以不太关注多重共线性问题？分布滞后模型（或机动）[实验目的]使学生掌握分布滞后模型的应用，能够解释估计结果，关键是可以对所建立的模型进行分析。

[实验内容]①分布滞后模型参数估计；②回归结果的解释[实验步骤]数据导入—模型参数估计—回归结果的解释案例6.1以1996－2005年全国广义货币供应量和物价指数的月度数据（见表6-1）利用分布滞后模型研究了货币增长率对消费价格的影响问题。

为了考察货币供应量的变化对物价的影响，我们用广义货币M2的月增长量M2Z 作为解释变量，以居民消费价格月度同比指数TBZS 为被解释变量进行研究。

首先估计如下回归模型:tt t Z M TBZS εβα++=20表6-11996－2005年全国广义货币供应量及物价指数月度数据月度广义货币M2(千亿元）广义货币增长量M2Z （千亿元）居民消费价格同比指数TBZS月度广义货币M2(千亿元）广义货币增长量M2Z （千亿元）居民消费价格同比指数TBZS Jan-9658.401Oct-00129.522-0.9518100Feb-9663.778 5.377109.3Nov-00130.9941 1.4721101.3Mar-9664.5110.733109.8Dec-00134.6103 3.6162101.5Apr-9665.723 1.212109.7Jan-01137.5436 2.9333101.2May-9666.88 1.157108.9Feb-01136.2102-1.3334100Jun-9668.132 1.252108.6Mar-01138.7445 2.5343100.8Jul-9669.346 1.214108.3Apr-01139.9499 1.2054101.6Aug-9672.3092.963108.1May-01139.0158-0.9341101.7Sep-9669.643-2.666107.4Jun-01147.80978.7939101.4 Oct-9673.1522 3.5092107Jul-01149.2287 1.419101.5 Nov-9674.1420.9898106.9Aug-01149.94180.7131101 Dec-9676.0949 1.9529107Sep-01151.8226 1.880899.9 Jan-9778.648 2.5531105.9Oct-01151.4973-0.3253100.2 Feb-9778.9980.35105.6Nov-01154.0883 2.59199.7 Mar-9779.8890.891104Dec-01158.3019 4.213699.7 Apr-9780.8180.929103.2Jan-02159.6393 1.337499 May-9781.1510.333102.8Feb-02160.9356 1.2963100 Jun-9782.789 1.638102.8Mar-02164.0646 3.12999.2 Jul-9783.460.671102.7Apr-02164.57060.50698.7 Aug-9784.746 1.286101.9May-02166.061 1.490498.9 Sep-9785.892 1.146101.8Jun-02169.6012 3.540299.2 Oct-9786.6440.752101.5Jul-02170.8511 1.249999.1 Nov-9787.590.946101.1Aug-02173.2509 2.399899.3 Dec-9790.9953 3.4053100.4Sep-02176.9824 3.731599.3 Jan-9892.2114 1.2161100.3Oct-02177.29420.311899.2 Feb-9892.024-0.187499.9Nov-02179.7363 2.442199.3 Mar-9892.015-0.009100.7Dec-02185.0073 5.27199.6 Apr-9892.6620.64799.7Jan-03190.4883 5.481100.4 May-9893.936 1.27499Feb-03190.1084-0.3799100.2 Jun-9894.6580.72298.7Mar-03194.4873 4.3789100.9 Jul-9896.314 1.65698.6Apr-03196.1301 1.6428101 Aug-9897.2990.98598.6May-03199.5052 3.3751100.7 Sep-9899.795 2.49698.5Jun-03204.9314 5.4262100.3 Oct-98100.8752 1.080298.9Jul-03206.1931 1.2617100.5 Nov-98102.229 1.353898.8Aug-03210.5919 4.3988100.9 Dec-98104.4985 2.269599Sep-03213.5671 2.9752101.1 Jan-99105.5 1.001598.8Oct-03214.46940.9023101.8 Feb-99107.778 2.27898.7Nov-03216.3517 1.8823103 Mar-99108.4380.6698.2Dec-03221.2228 4.8711103.2 Apr-99109.2180.7897.8Jan-04225.10193 3.87913103.2 May-99110.0610.84397.8Feb-04227.05072 1.94879102.1 Jun-99111.363 1.30297.9Mar-04231.6546 4.60388103 Jul-99111.4140.05198.6Apr-04233.62786 1.97326103.8 Aug-99112.827 1.41398.7May-04234.8424 1.21454104.4 Sep-99115.079 2.25299.2Jun-04238.42749 3.58509105 Oct-99115.390.31199.4Jul-04234.8424-3.58509105.3 Nov-99116.559 1.16999.1Aug-04239.72919 4.88679105.3 Dec-99119.898 3.33999Sep-04243.757 4.02781105.2 Jan-00121.22 1.32299.8Oct-04243.74-0.017104.3 Feb-00121.58340.3634100.7Nov-04247.13558 3.39558102.8Mar-00122.58070.997399.8Dec-04253.2077 6.07212102.4 Apr-00124.1219 1.541299.7Jan-05257.75283 4.54513101.9 May-00124.0533-0.0686100.1Feb-05259.3561 1.60327103.9 Jun-00126.6053 2.552100.5Mar-05264.5889 5.2328102.7 Jul-00126.3239-0.2814100.5Apr-05266.99266 2.40376101.8 Aug-00127.79 1.4661100.3May-05269.2294 2.23674101.8 Sep-00130.4738 2.6838100数据来源：中经网统计数据库/导入数据，拟合得到如下的回归结果。