4-2 Central Limit Theorem-中心极限定理

中心极限定理两个公式中心极限定理是概率论中的一个重要定理，它描述了独立同分布随机变量的和服从正态分布的近似情况。

在统计学中，中心极限定理是数据分析和推论中非常重要的基本原理，它为我们提供了进行参数估计和假设检验的理论基础。

1.李雅普诺夫定理：设X1、X2、..、Xn是独立同分布的随机变量，具有相同的均值μ和方差σ^2（标准差σ），并且其生成函数M(t)存在，则对于任意ε>0，有lim [n->∞] P(∣(X1+X2+...+Xn)/n -μ∣<ε√n)=1/√(2π) ∫（-∞到∞） exp(-t^2/2)dt该定理表明当n足够大时，随机变量的和(X1+X2+...+Xn)/n的概率分布可近似地看作一个均值为μ，标准差为σ/√n的正态分布。

也就是说，当样本容量增加时，样本均值的分布趋向于正态分布。

这一结果对于大样本条件下的统计推断非常重要，它使我们得以在很多场景中应用正态分布进行推论，而不受具体分布函数的限制。

2.林德伯格定理（也称为林德伯格-列维定理）：设X1、X2、..、Xn是独立同分布的随机变量，具有相同的均值μ和方差σ^2（标准差σ），并且其矩生成函数存在，则对于任意ε>0，有lim [n->∞] P(∣(X1+X2+...+Xn)/n -μ∣<ε√n)=1/√(2πσ^2)∫（-∞到∞） exp(-(t-μ)^2/2σ^2)dt这个定理在独立同分布的随机变量的和的极限分布建立了正态分布的形式。

与李雅普诺夫定理不同的是，林德伯格定理对矩生成函数的存在有一定的要求。

矩生成函数是随机变量的一个重要特征，它能够唯一地确定随机变量的分布。

因此，林德伯格定理对于具有矩生成函数的随机变量的和能够提供更为精确的正态分布近似。

1.样本均值的分布近似：当样本容量很大时，根据中心极限定理，样本均值的分布近似为正态分布，这为统计推断提供了数理依据。

例如，我们可以根据样本均值的正态分布性质进行参数估计和假设检验。

中心极限定理与大数定律介绍中心极限定理（Central Limit Theorem）和大数定律（Law of Large Numbers）是概率论中两个重要而基础的定理。

它们在统计学和各个领域的实际应用中起着至关重要的作用。

本文将深入探讨这两个定理的概念、应用和相关证明。

中心极限定理定义中心极限定理是概率论中的一个重要定理，它说明了在特定条件下，一组随机变量的均值的分布会趋近于正态分布。

具体来说，对于任意独立同分布的随机变量的和，当样本容量足够大时，其均值的分布将会接近于正态分布。

证明中心极限定理的证明可以通过多种方法进行推导，其中最为经典的方法是使用特征函数的技巧。

通过对特征函数的逐步展开和极限取证，可以得出中心极限定理的结论。

应用中心极限定理在实际应用中有着广泛的应用。

以下是中心极限定理的几个重要应用：1.抽样分布的近似计算：通过中心极限定理，可以对抽样分布进行近似计算，从而推断总体参数。

2.假设检验：在统计学中，中心极限定理广泛应用于假设检验问题中。

通过对样本均值进行正态分布近似，可以进行对总体均值的假设检验。

3.建立置信区间：中心极限定理可用于建立置信区间。

通过计算样本均值的区间估计，确定总体均值的信心水平。

大数定律定义大数定律是概率论中的另一个重要定理，它说明了当独立同分布的随机变量重复进行实验时，其平均值会收敛于数学期望。

换句话说，随着实验次数的增加，样本均值会趋近于总体均值。

证明大数定律的证明有多种方法，其中最为著名的是切比雪夫不等式和辛钦大数定律。

不同的证明方法都有其特点和适用范围，但最终都能得出大数定律的结论。

应用大数定律在实际应用中也有着广泛的应用。

以下是大数定律的几个重要应用：1.统计估计：大数定律可用于建立统计估计方法，如最大似然估计和矩估计。

2.贝叶斯推断：大数定律在贝叶斯推断中起着重要的作用。

通过重复实验，可以逐渐更新对参数的先验分布，得到后验分布。

3.经济学和金融学：大数定律在经济学和金融学中有广泛的应用。

中心极限定理（central limit theorem/CLT）是概率论（probability theory）一个非常重要的结论，它指出在一定条件下，独立（independent）随机变量的标准化的（normalized）和随样本量（sample size）变大会趋向正态分布（normal distribution），即它的累积分布函数（cumulative distribution function/CDF）会收敛于标准正态分布（standard normal distribution）的CDF N(x)=∫−∞x12πe−x2/2 dx。

中心极限定理不要求随机变量本身是正态分布的，所以它带来一个非常重要的结果：在一定条件下，我们可以使用对正态分布成立的方法去应对非正态分布。

比如，对于样本量n足够大时，二项分布（binomial distribution）Bin(n,p)可以用正态分布N(np,np(1−p))来近似。

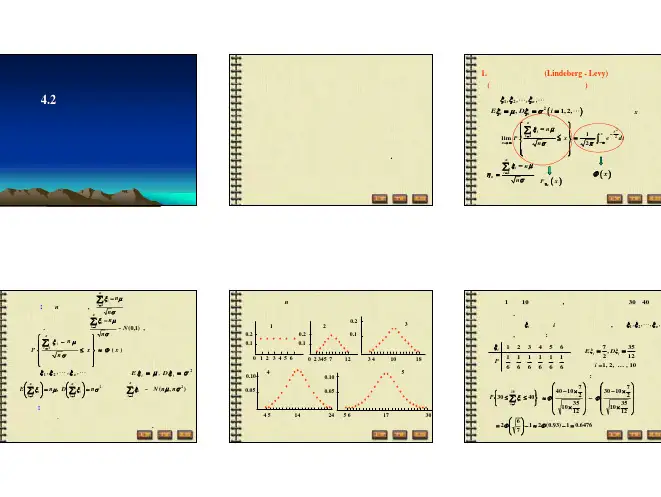
大样本理论公式整理中心极限定理大数定律的推导与应用大样本理论公式整理：中心极限定理、大数定律的推导与应用在统计学中，大样本理论是一种基本的概念，它为我们提供了一些重要的工具来进行数据分析和推断。

其中，中心极限定理和大数定律是大样本理论中最为关键的两个定理。

本文将对这两个定理进行推导，并探讨它们在实际应用中的意义和应用方法。

一、中心极限定理的推导中心极限定理 (Central Limit Theorem, CLT) 是大样本理论的核心内容之一，它说明了在很多独立随机变量的和的情况下，当样本容量趋于无穷大时，该和的分布将近似服从正态分布。

设有n个独立随机变量X1, X2, ..., Xn，它们的期望值分别为μ，方差分别为σ^2。

令S_n = X1 + X2 + ... + Xn，则S_n的期望值为E(S_n)= μn，方差为Var(S_n) = σ^2n。

根据大样本理论，当n趋于无穷大时，S_n的分布将近似服从正态分布，即：S_n ～N(μn, σ^2n) (1)这意味着当我们对一个足够大的样本进行抽样和求和时，样本均值的分布将近似符合正态分布。

二、大数定律的推导大数定律 (Law of Large Numbers, LLN) 揭示了当样本容量趋于无穷大时，样本均值将收敛到总体均值。

设有n个独立同分布的随机变量X1, X2, ..., Xn，它们的期望值为μ，方差为σ^2。

令X = (X1 + X2 + ... + Xn)/n，表示样本的均值。

根据大数定律，当n趋于无穷大时，X将以概率1收敛到μ，即：lim(n→∞) P(|X - μ| ≥ ε) = 0 (2)其中ε为任意正数。

这表明当样本容量足够大时，样本均值将趋近于总体均值。

三、中心极限定理和大数定律的应用中心极限定理和大数定律作为统计学中重要的理论基础，广泛应用于实际数据分析和推断过程中。

1. 抽样分布的应用基于中心极限定理，我们可以利用样本均值的正态分布特性，进行抽样分布的推断。

大数定律与中心极限定理知识点整理大数定律和中心极限定理是概率论与数理统计中两个重要的概念，它们在统计学和经济学等领域中具有广泛的应用。

下面将对它们的主要知识点进行整理。

一、大数定律（Law of Large Numbers）大数定律是关于随机变量序列均值的收敛性的一个法则。

它表明，当独立同分布的随机变量不断增加时，其均值将会趋近于理论期望。

具体来说，大数定律包含以下几个重要概念：1. 弱大数定律（Weak Law of Large Numbers）弱大数定律指的是当随机变量序列无限增加时，其均值以概率1收敛于理论期望。

这个定律要求序列中的随机变量具有有限的方差和独立同分布的性质。

2. 强大数定律（Strong Law of Large Numbers）强大数定律指的是当随机变量序列无限增加时，其均值几乎处处收敛于理论期望。

与弱大数定律相比，强大数定律要求序列中的随机变量只需要具有独立性，而不需要具有方差的有限性。

二、中心极限定理（Central Limit Theorem）中心极限定理是关于随机变量和其样本均值之间关系的一个重要定理。

它表明，当样本量增加时，随机变量的分布将趋近于正态分布。

中心极限定理包含以下几个关键点：1. 独立同分布的随机变量之和的分布趋近于正态分布。

2. 标准化后的样本均值的分布趋近于标准正态分布。

3. 样本量越大，越接近正态分布。

总结：大数定律和中心极限定理是概率论与数理统计中非常重要的概念。

大数定律研究随机变量序列均值的收敛性，而中心极限定理研究随机变量和其样本均值的分布趋近于正态分布的关系。

它们的应用广泛，对于统计学、经济学等领域的研究与实践具有重要意义。

二项分布的中心极限定理中心极限定理（Central Limit Theorem，CLT）是概率论中一项重要而强大的定理，它深刻地阐述了二项分布在特定条件下的极限行为。

本文以生动的方式解释中心极限定理的含义和应用，并为读者提供一些指导意义。

二项分布是离散概率分布的一种形式，它描述了在n次独立重复试验中成功的次数。

例如，在投硬币的实验中，假设我们连续投掷n 次，每次的成功定义为正面朝上，失败定义为反面朝上。

如果硬币是公平的，我们可以用二项分布来描述在n次投掷中正面朝上的次数。

具体而言，二项分布的概率质量函数可以表示为：P(X=k) = C(n,k) * p^k * (1-p)^(n-k)其中，P(X=k)表示在n次试验中成功k次的概率，C(n,k)是组合数，p是每次试验成功的概率，(1-p)则是失败的概率。

然而，当我们试图从一个很大的二项分布中计算和理解结果时，面临的计算和解释难题可能会变得非常困难。

这时，中心极限定理的出现就提供了一个非常有用的近似方法。

中心极限定理指出，当n足够大时，二项分布可以近似地由正态分布来描述。

简单地说，中心极限定理表明，当我们进行大量独立试验时，这些试验的和或平均值将呈现出近似正态分布的特性。

这一定理适用于满足一定条件的任何概率分布，不仅仅适用于二项分布。

这个定理的实际含义是什么呢？以一个例子解释可能更容易理解。

假设我们有一个非常大的人群，每个人都独立地做一个有二项分布的任务，而每个任务成功的概率相同。

例如，我们可能在一个足球场上观察所有观众的掌声情况。

如果我们测量来自每个观众的掌声次数，并将这些次数相加，根据中心极限定理，这个总和将近似为一个正态分布。

通过使用正态分布来近似二项分布，我们可以更好地理解和分析问题。

正态分布具有许多有用的性质，例如，我们可以用均值和标准差来描述它，从而更好地理解数据的变异性和趋势。

此外，通过计算正态分布的概率密度函数或使用标准正态分布表，我们可以计算和解释我们感兴趣的事件概率。

供应链管理的18条原理1、本福德定律（Benford’s Law）定义：从1开头的数字出现的频率是以9开头的数字出现频率的6倍，说得具体一些，预测得到的各数字出现的概率如下：1出现的概率为30.1%，2出现的概率为17.6%，3出现的概率为12.5%，4出现的概率为9.7，5出现的概率为6.7%，7出现的概率为5.8%，8出现的概率为5.1%，9出现的概率为4.6%。

含义：人们通常认为各个数字出现在首位的可能性大致是相等的，这意味着如果一组数据，其首位数字出现频率基本一致，那么这组数据很可能是捏造的虚假数据，或者可以成为造假的潜在证据。

2、牛鞭效应（Bullwhip Effect）定义：观察到的需求变动沿供应链向上时会逐渐增加。

例如：消费者在零售商处的需求变动较之生产订单要稳定。

含义：牛鞭效应会导致供应链的高成本和低服务。

我们要理解造成牛鞭效应产生的原因，并通过控制这些成因来限制牛鞭效应的发生。

3、中心极限定理（Central Limit Theorem）定义：当独立随机变量的数量增加，其总体的概率分布接近服从正态分布。

含义：任意措施带来的利益经常包括许多独立随机因素。

在这里情况下，根据正态分布对不确定的分析是一个很好的估计。

4、利用率诅咒（Curse of Utilization）定义：当资源利用率接近100%时，平均流程时间猛增。

含义：系统或资源利用率是系统或资源处于忙碌状态下的时间百分比。

除非过程的可变性很小，否则，提供响应的资源将不可能得到充分的利用。

5、可变性诅咒（Curse of Variability）定义：可变性导致拥堵。

含义：在过程中寻找降低变化性的方法。

6、肥头效应(Fat Head Effect)定义：人们对自身的决策能力有过分自信的倾向。

含义：识别潜藏在你决策中的心智模式偏见是很困难的。

在判断中保持批评和谦虚的态度，并且从别处获取真诚的建议。

7、冰球棒效应(Hockey Stick Effect)定义：在接近报告周期尾声的时候，数量和活动性就会增加。

浅谈中心极限定理及其应用中心极限定理（CentralLimitTheorem，简称CLT）是统计学中最基本的定理，可以提供数学理论支持和方便的引用，以解决许多实际问题。

这个定理的完整表述是：当抽取的样本量足够大的时候，样本平均数的分布曲线接近于正态分布，即属于类正态分布，其平均值接近于总体平均数，其标准差接近于总体标准差的平方根。

中心极限定理的应用方面，可以涉及到许多方面：一、测定总体参数。

中心极限定理可以用来估计总体参数，包括总体均值、总体方差和总体分布等。

二、假设检验。

中心极限定理可以用于检验统计模型的参数，即样本和总体的分布形式是否一致，研究者可以利用其来进行假设检验，从而评估统计模型的正确性。

三、置信区间估计。

中心极限定理也可以利用来估计总体参数所处的置信区间，在样本量足够大的情况下，置信区间会变得紧密，从而使得置信度得到提高。

四、回归分析。

在回归分析中，中心极限定理可用于评估模型的参数置信区间，也可用于评估线性回归模型的拟合程度，从而推出结论。

具体来讲，中心极限定理的应用非常灵活，并且无处不在，几乎所有的统计分析和统计模型都可以借助它求解。

在实际数据处理中，中心极限定理是统计学中最基本定理，将它运用在模型构建中，将有助于增强模型的可靠性和准确性。

总之，中心极限定理可以用来估计总体参数，也可以用于假设检验，能够确定模型的参数，估计总体参数所处的置信区间范围，及对回归分析进行验证。

它是统计学基础理论，在数据处理中起着重要作用，为研究者提供了便利。

中心极限定理实际上是一个概率模型，它可以分析我们观察到的大量数据，帮助我们做出更准确的决策。

而且，它也是数据挖掘和机器学习的基础理论，对于统计数据处理和模型建立有着重要意义。

中心极限定理的基本概念和应用场景中心极限定理（Central Limit Theorem）是概率论和统计学中的重要定理之一，它描述了在某些条件下，大量独立同分布随机变量的和的分布会近似服从正态分布。

该定理的重要性在于它提供了一种解决实际问题时的近似方法，其应用场景涵盖了各个领域。

一、中心极限定理的基本概念中心极限定理基于大数定律及正态分布的性质，其基本概念可归纳为以下几点：1. 大数定律大数定律指出对于独立同分布随机变量而言，随着样本容量的增大，随机变量的平均值收敛于其数学期望。

这意味着当样本量充足时，可以准确估计出总体的特征。

2. 正态分布正态分布是一种对称的连续概率分布，具有均值为μ、标准差为σ的特征。

在正态分布中，均值、中位数和众数是相等的，呈现出钟型曲线的形态。

许多随机现象在一定条件下可以近似地服从正态分布。

3. 中心极限定理中心极限定理描述了当独立同分布随机变量的样本容量足够大时，其和的分布将近似于正态分布。

我们可以通过计算样本的均值与标准差来评估总体参数，并进行各类假设检验和置信区间估计。

二、中心极限定理的应用场景中心极限定理在实际问题中有广泛的应用，以下介绍几个常见的应用场景：1. 抽样调查在社会科学和市场调研中，抽样调查是获取数据的重要方式。

利用中心极限定理，我们可以通过随机抽样的方式获取样本数据，并利用样本数据的均值和标准差来估计总体参数，如人口普查、选民调查等。

2. 假设检验假设检验是统计学中对某个假设进行科学验证的一种方法。

中心极限定理使得我们可以通过计算样本均值和标准差，进而得到服从正态分布的统计量，进行假设检验。

例如，医学研究中对某种新药疗效的检验、市场营销中对广告效果的评估等。

3. 投资风险评估在金融领域，投资风险评估是一项重要的任务。

中心极限定理可以用于评估一揽子投资组合的风险分布情况，预测其潜在的回报和风险水平，并为投资决策提供科学依据。

4. 信号处理在信号处理领域，中心极限定理被广泛应用于噪声信号的处理和恢复过程中。

大数定律和中心极限定理大数定律（Law of Large Numbers）是概率论中的一个重要定理，它揭示了在一系列独立随机事件中，随着样本量的增大，样本均值将趋于总体均值的规律。

中心极限定理（Central Limit Theorem）则是统计学中的一项基本定理，它说明了在大样本条件下，一组独立随机变量的和具有近似正态分布的特性。

两个定理在统计分析和推断中都起到了重要作用。

大数定律（Law of Large Numbers）大数定律是概率论中的一个基础定理，它描述了独立随机事件的平均值在大样本条件下会无限接近于事件的真实概率。

根据大数定律，当独立随机事件重复进行时，样本均值将逐渐接近总体均值。

大数定律有两种形式：辛钦大数定律和伯努利大数定律。

辛钦大数定律是指当随机变量的期望存在时，样本均值以概率1收敛于期望值。

也就是说，无论一个事件发生的可能性有多小，只要重复进行足够多的实验，该事件发生的频率将无限接近于其概率。

伯努利大数定律是针对二项分布的情况，它说明了在一系列独立重复的二项试验中，随着试验次数的增加，事件发生的频率将逐渐接近于事件的概率。

大数定律在实际应用中有着广泛的作用。

例如，投资者根据历史数据计算股票收益率的期望，大数定律告诉我们当样本容量足够大时，计算得到的样本均值将逼近真实的期望收益率，从而提供了对未来股票表现的一定参考。

中心极限定理（Central Limit Theorem）中心极限定理是统计学中的一项基本定理，它指出在大样本条件下，一组独立随机变量的和具有近似正态分布的特性。

中心极限定理是统计学中推断的基础，它的重要性在于它使得我们可以利用正态分布的性质进行概率和置信区间的计算。

中心极限定理的表述可以分为两种形式：李雅普诺夫型和林德伯格-李维定理。

李雅普诺夫型定理给出了随机变量和的分布函数收敛到正态分布的条件，其中随机变量可以不是独立同分布的。

林德伯格-李维定理则是对独立同分布随机变量和的和近似服从正态分布的定理。

中心极限定理名词解释
中心极限定理（Central Limit Theorem）是统计学中最重要的定理之一，它指出，当一组
数据的样本数足够大时，它们的分布接近正态分布，即钟形曲线。

中心极限定理的发现是由法国数学家卡尔·贝尔所做的，他在1733年发表了他的著作《数
学原理》，其中提出了中心极限定理。

他的定理指出，当一组数据的样本数足够大时，它们的分布接近正态分布，即钟形曲线。

中心极限定理的重要性在于它提供了一种简单的方法来估计一组数据的分布，而不必考虑
其中的每一个数据点。

它还提供了一种简单的方法来估计一组数据的均值和方差，从而使统计学家能够更好地理解数据。

中心极限定理的应用非常广泛，它可以用于统计学、金融学、社会科学等领域。

它可以用
来估计一组数据的均值和方差，从而更好地理解数据。

它还可以用来估计投资组合的风险，从而帮助投资者做出更明智的投资决策。

总之，中心极限定理是一个非常重要的定理，它为统计学、金融学、社会科学等领域提供了一种简单而有效的方法来估计一组数据的分布，从而帮助我们更好地理解数据。

中心极限定理公式中心极限定理（Central Limit Theorem）是概率论中的一个重要定理，它可以描述一类随机变量的分布特性。

该定理的公式形式如下：设X₁, X₂, ..., Xₙ是独立同分布的随机变量，它们具有相同的概率分布，且具有有限的均值μ和方差σ²。

令Sₙ = (X₁ + X₂ + ...+ Xₙ) / √n，则当n趋近于无穷大时，随机变量Sₙ的分布趋近于正态分布，其均值为μ，方差为σ²/n。

中心极限定理被认为是概率论和统计学的一个基本定理，它在理论和实际应用中都起到了至关重要的作用。

它的核心思想是，当一个随机变量是由大量相互独立的随机事件叠加而成时，其分布趋向于正态分布。

这意味着即使原始随机变量的分布不是正态分布，但当样本数足够大时，样本均值的分布将接近于正态分布。

中心极限定理的生动性在于它提供了一个如何从大量随机事件中得到可靠结论的方法。

假设我们想要研究某地区居民的身高。

如果我们直接从全体居民中随机抽取一些人，可能面临样本不足、样本不具有代表性等问题。

而中心极限定理告诉我们，只要我们能够抽取足够数量的样本，样本均值的分布将逐渐接近正态分布，从而能够提供关于全体居民身高的合理估计。

中心极限定理的全面性在于它适用于各种类型的随机变量。

无论原始分布是均匀分布、指数分布、二项分布还是任何其他形式，只要满足独立同分布的条件，中心极限定理都成立。

这使得中心极限定理成为处理实际问题的有力工具。

不论我们需要研究某种产品的质量、市场的需求量，还是其他任何具有随机性的现象，中心极限定理都可以帮助我们得到更准确的结果。

中心极限定理的指导意义在于它可以为我们提供关于样本大小的参考。

根据中心极限定理的要求，当我们想要得到一个具有一定可靠性的估计值时，我们需要确保样本数足够大。

通常，当样本数超过30时，中心极限定理的近似效果足够好；当样本数超过100时，其近似效果更加显著。

因此，在实际应用中，我们可以根据中心极限定理的指导，选择适当的样本大小，以获得可靠的结果。

中心极限定理应用举例1 中心极限定理中心极限定理（Central Limit Theorem）是统计学中的一个基本定理，它认为当某一总体的随机变量（不论其服从的分布形式）经过加权求和或取均值之后，其分布的形态将近似于正态分布，而且其拥有正态分布的各项统计量（如均值、方差）。

因此，它被用于统计抽样和统计假设检验的统计假说的验证。

2 中心极限定理的原理中心极限定理的原理是指当样本大小趋于无穷时，无论是服从什么分布的概率密度函数，样本均值的分布近似满足正态分布。

当抽取的样本从某一个总体中来，而且样本是无关独立的抽样，那么抽样的平均值的概率分布将接近正态分布。

样本的数量越大，曲线越缠曲，钟形曲线越完美，也就是越接近正态分布。

中心极限定理对实验结果有很强的支撑作用，为统计计算提供了依据，是统计学中最重要的一个定理。

3 中心极限定理的应用中心极限定理在现实世界中有着广泛的应用。

（1）中心极限定理可以用来确定抽样分布与总体分布的关系，从而进行总体推断。

根据中心极限定理，当抽样数量越多，抽样的结果越来越接近总体的特征，因此，大量的抽样可以用来推断总体的特性。

（2）中心极限定理也可以用来进行统计假设检验。

在大量的抽样的情况下，将抽样的结果当做正态分布，进行统计检验，可以反映出样本的概率特征，从而可以准确地对实验结果进行分析。

4 中心极限定理举例比如，统计学家在研究一种药物的有效性时，临床研究中可能会涉及几乎无数的患者，随机分配到接受该药物治疗和控制组，然后分析两组的治疗疗效是否存在显著性差异。

这时，中心极限定理就可以起到至关重要的作用，可以将两组的治疗效果差异归结为正态分布，并且可以用统计检验方法来进行有效性判断，有效地确定出最佳治疗疗效。

中心极限定理 30个样本
中心极限定理（central limit theorem, CLT）是概率论中的一个重要定理，指的是当样本容量足够大时，一组独立同分布的随机变量的和的分布近似地服从正态分布。

具体来说，中心极限定理表明，对于一个独立同分布的随机变量序列X1, X2,..., Xn，其均值的分布（即样本均值）服从正态分布，即
lim(n->∞) P((X1+X2+...+Xn - nμ)/√(nσ^2)) ≤ x) =
Φ(x)
其中，μ是随机变量的期望，σ是随机变量的标准差，Φ(x)是标准正态分布的累积分布函数。

根据中心极限定理，当样本容量n足够大时，其样本均值的分布近似于正态分布。

这意味着，对于较大的样本量，即使原始数据并不服从正态分布，其样本均值的分布也会趋近于正态分布。

在中心极限定理中，并没有明确给出样本量需要达到多少才能满足近似正态分布的条件，一般认为当样本容量n大于30时，中心极限定理适用性较好。

因此，当我们有30个独立同分布的样本时，可以认为样本均值的分布近似服从正态分布。

中心极限定理公式掌握中心极限定理的关键公式中心极限定理公式掌握- Central Limit Theorem Formula:中心极限定理（Central Limit Theorem）是统计学中一个非常重要的概念，它描述了一种现象：当独立随机变量的和具有相同的分布时，这些随机变量的和在样本量足够大的情况下，将近似地服从正态分布。

在实际应用中，掌握中心极限定理的关键公式是非常重要的。

公式如下所示：若X₁, X₂, ..., Xₙ是取自于总体X的一个随机样本，且总体X的均值为μ，方差为σ²。

当n趋近于无穷大时，X₁+X₂+...+Xₙ的极限分布是正态分布。

其中，极限分布的均值为nμ，方差为nσ²，即：X₁+X₂+...+Xₙ ~ N(nμ, nσ²)这个公式在统计学中广泛应用，特别是当样本量较大时，可以用来近似计算各种统计量的分布。

利用中心极限定理，我们可以在不了解总体分布的情况下，利用样本数据进行统计推断。

举个例子来说明这个公式的应用。

假设某地区的一批学生身高服从正态分布，均值为165cm，标准差为5cm。

我们对该地区的100名学生进行抽样调查，测量他们的身高并计算均值。

根据中心极限定理，样本均值的分布近似服从正态分布，均值为总体均值165cm，方差为总体方差除以样本量，即5²/100=0.25。

因此，可以套用中心极限定理的公式：样本均值 ~ N(165, 0.25)可以利用这个正态分布计算各种置信区间、假设检验以及预测等问题。

中心极限定理的关键公式成为了统计学中进行推断的重要工具。

除了样本均值外，样本比例、样本差等统计量也可以利用中心极限定理进行近似计算。

公式的核心思想是将多个独立随机变量的和化归为一个近似服从正态分布的随机变量，从而简化统计推断的计算过程。

总结起来，中心极限定理公式为：X₁+X₂+...+Xₙ ~ N(nμ, nσ²)这个公式被广泛应用于统计学中，可以帮助我们在不了解总体分布的情况下进行各种统计推断。

clt中心极限定理中心极限定理（CentralLimitTheorem,CLT）是统计学中最重要的定理之一，它揭示了随机变量和它们的样本均值之间的关系。

CLT 的核心思想是，对于任何一组独立随机变量，它们的样本均值的分布趋近于正态分布，即使这些随机变量本身并不服从正态分布。

CLT是由法国数学家拉普拉斯（Pierre-Simon Laplace）在1810年左右首次提出的，但在19世纪中叶才得到了广泛的认可。

现在，CLT已经成为了统计学中的基础理论之一，应用广泛，包括金融、经济、医学、社会科学等多个领域。

CLT的形式可以分为三种不同的形式：极限形式、拉格朗日形式和李雅普诺夫形式。

其中，极限形式是最常见的形式，它的表述是：对于独立同分布的随机变量$X_1,X_2,...,X_n$，它们的样本均值$bar{X}$的分布，随着$n$的增大而趋近于正态分布：$$sqrt{n}(bar{X}-mu)rightarrow N(0,sigma^2)$$ 其中，$mu$是$X_i$的均值，$sigma^2$是$X_i$的方差，$N(0,sigma^2)$表示均值为0，方差为$sigma^2$的正态分布。

CLT的重要性在于它提供了一个通用的方法来处理样本均值的分布问题。

例如，在实际应用中，我们通常不能确定一个随机变量的分布，但是，如果我们知道它的样本均值的分布是正态分布，那么我们就可以利用正态分布的一些性质来进行推断和预测。

此外，CLT还有一些重要的推论，例如：1. 样本均值的标准误（standard error）随着样本量的增加而减小。

标准误是样本均值与总体均值之间的标准差，它是样本均值的不确定度的度量。

根据CLT，当样本量足够大时，标准误的大小趋近于0，这意味着我们对总体均值的估计更加准确。

2. 样本均值的置信区间（confidence interval）越窄，置信水平（confidence level）越高。