小学四年级数学三角形的分类(知识点梳理+典型例题)

小学四年级数学三角形的分类(知识点梳理+典型例题)三角形的相关概念考点一【三角形的特性】三角形的定义：由三条线段围成的图形（每相邻两条线段的端点相连）叫做三角形三角形的高：从三角形的一个顶点到它的对边做一条垂线，顶点和垂足之间的线段三角形的底：这条对边叫做三角形的底用字母A、B、C分别表示三角形的三个顶点，这个三角形可以表示成三角形ABC三角形的性质：①物理特性：三角形具有稳定性（不易变形）②三边的特性：三角形任意两边的和大于第三边知识典例题型一：画出三角形的底边上的高例1：画出下面每个三角形底边上的高。

例2：画三条不同的高1题型二：三角形的内角和例1、王爷爷家的屋顶是一个等腰例2、根据三角形的内角和是180°，三角形（如图），求顶角的度数。

你能求出下面五边形的内角和吗？例3、一个三角形两个内角的度数分别为35°，67°，另一个内角的度数是（）°，这是一个（）三角形。

例4、在一个直角三角形中，一个锐角是75°，另一个锐角是（）。

题型三：等腰三角形和等边三角形的性质例1.一个三角形三条边的长度分别为7厘米，8厘米，7厘米，这个三角形是（）三角形。

例2.等腰三角形的底角是75°，顶角是（），等边三角形的每个内角都是（）。

例3.一个等腰三角形的一边长5厘米，另一边长4厘米，围成这个等腰三角形至少需要（）厘米长的绳子。

例4.在一个三角形的三个角中，一个是50度，一个是80度，这个三角形既是（）三角形，又是（）三角形。

题型四、求出三角形各个角的度数。

40°三角形的分类2考点一【三角形的分类】三角形（按角来分）锐角三角形：三个角都是锐角的三角形直角三角形：有一个角是直角的三角形钝角三角形：有一个角是钝角的三角形三角形（按边来分）三边不等三角形：三条边都不相等等腰三角形：有两条边相等等边三角形（正三角形）：三条边都相按照角大小来分：三角形，三角形，三角形。

三角形的分类与性质（知识点总结）三角形是几何学中的基本图形之一，其分类与性质是我们学习和掌握三角形知识的基础。

本文将对三角形的分类以及其相关性质进行总结，以帮助读者更好地理解和应用相关概念。

一、三角形的分类根据三角形的边长长短和角度大小，三角形可以分为以下几类：1.按边长分类：（1）等边三角形：三条边的长度相等。

（2）等腰三角形：两条边的长度相等。

（3）普通三角形：三条边的长度各不相等。

2.按角度大小分类：（1）锐角三角形：三个内角均小于90度。

（2）直角三角形：其中一个内角为90度。

（3）钝角三角形：其中一个内角大于90度。

3.根据边长和角度分类的组合：根据边长和角度的不同组合，可以得到以下三角形的特殊分类：（1）等边等角三角形：即正三角形，三个内角均为60度，且三条边长度相等。

（2）等腰直角三角形：拥有一个直角，且两条腰的长度相等。

（3）等腰锐角三角形：拥有两个锐角，且两条腰的长度相等。

（4）等腰钝角三角形：拥有一个钝角，且两条腰的长度相等。

二、三角形的性质除了分类外，三角形还有一些重要的性质值得我们关注和记忆：1.内角和：任意三角形的三个内角和等于180度。

2.角的关系：（1）锐角三角形中，三个内角的大小按大小顺序排列即可。

(如A<B<C)（2）直角三角形中，其中一个内角为90度，另外两个内角互为补角。

（3）钝角三角形中，其中一个内角大于90度，另外两个内角的和小于90度。

3.边的关系：（1）等边三角形的三条边长度相等。

（2）等腰三角形的两个底角（等腰三角形两腰之间的夹角）相等。

（3）等腰直角三角形中，两条腰的长度相等，且斜边是两腰长度的平方和的平方根。

4.勾股定理：勾股定理是直角三角形最重要的定理，描述了直角三角形斜边平方等于两直角边平方和的关系。

5.海伦公式：海伦公式用于计算任意三角形的面积，公式为：面积 = （p * (p - a) * (p - b) * (p - c)）的平方根，其中p为三角形的半周长，a、b、c为三角形的三条边长。

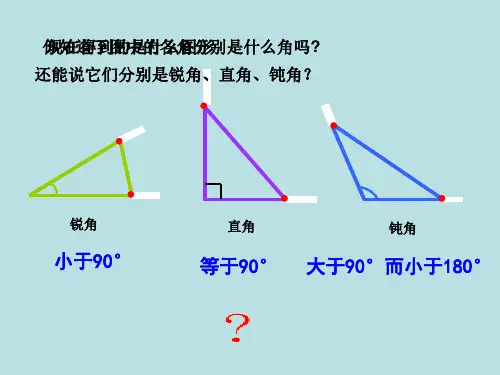
四年级三角形题型汇总一、三角形的认识基础题型1. 判断三角形类型（按角分）题目：一个三角形的三个角分别为30°、60°、90°，这个三角形是什么三角形？解析：三角形按角分为锐角三角形（三个角都是锐角，即小于90°）、直角三角形（有一个角是90°）、钝角三角形（有一个角大于90°小于180°）。

在这个三角形中，有一个角是90°，所以它是直角三角形。

2. 判断三角形类型（按边分）题目：一个三角形的三条边分别为3cm、3cm、4cm，这个三角形是什么三角形？解析：三角形按边分有等边三角形（三条边都相等）、等腰三角形（至少有两条边相等）、不等边三角形（三条边都不相等）。

这个三角形有两条边相等，都是3cm，所以它是等腰三角形。

二、三角形的内角和题型1. 已知两个角求第三个角题目：在一个三角形中，已知∠1 = 40°，∠2 = 60°，求∠3的度数。

解析：因为三角形的内角和是180°，所以∠3=180°∠1 ∠2。

即∠3 = 180°-40° 60° = 80°。

2. 根据内角和判断三角形类型（间接）题目：一个三角形的三个角的度数比是1:2:3，这个三角形是什么三角形？解析：设三个角分别为x、2x、3x。

因为三角形内角和为180°，所以x +2x+3x = 180°，6x = 180°，x = 30°。

那么三个角分别为30°、60°、90°，所以这个三角形是直角三角形。

三、三角形的边的关系题型1. 判断三条线段能否组成三角形题目：三条线段的长度分别为2cm、3cm、5cm，能否组成三角形？解析：根据三角形三边关系，任意两边之和大于第三边，任意两边之差小于第三边。

2 + 3 = 5，不满足两边之和大于第三边，所以这三条线段不能组成三角形。

三角形的种类知识点总结三角形是几何学中最基本的几何图形之一，由三条边和三个顶点组成。

根据边长和角度的不同，三角形可以分为不同的种类。

本文将对常见的三角形种类进行总结，以便帮助读者更好地理解和掌握相关知识。

一、按边长分类1.等边三角形：等边三角形指的是三条边的长度完全相等的三角形。

由于三边相等，所以对应的三个角也相等，都为60度。

这是一种特殊的等腰三角形。

2.等腰三角形：等腰三角形是指两条边的长度相等的三角形。

由于两边相等，所以对应的两个角也相等。

等腰三角形的顶角称为顶点角，其他两个角称为底角。

3.等腰直角三角形：等腰直角三角形是指两条边的长度相等且有一个直角的三角形。

因为有一个直角，所以其他两个角是锐角，且相等。

等腰直角三角形是勾股定理的基本示例。

4.不等边三角形：不等边三角形是指三条边的长度都不相等的三角形。

不等边三角形的三个角也不相等。

二、按角度分类1.锐角三角形：锐角三角形是指三个角都小于90度的三角形。

2.钝角三角形：钝角三角形是指三个角中有一个角大于90度的三角形。

3.直角三角形：直角三角形是指其中一个角等于90度的三角形。

直角三角形具有特殊的性质，其中两条边的平方和等于第三边的平方，被称为勾股定理。

三、按角度和边长分类1.等腰锐角三角形：等腰锐角三角形是指两条边相等，且三个角都小于90度的三角形。

2.等腰钝角三角形：等腰钝角三角形是指两条边相等，且其中一个角大于90度的三角形。

3.等腰直角三角形：等腰直角三角形是指两条边相等，且有一个角等于90度的三角形。

等腰直角三角形是勾股定理的特例。

综上所述，三角形按边长、角度或同时考虑边长和角度的不同可以分为多种种类。

理解这些基本的三角形种类对于学习和解决几何问题非常重要。

希望本文能够帮助读者更好地掌握三角形的分类知识。

一、概念与特点1.三角形是由三条线段所围成的图形，它有且只有三个顶点、三条边和三个内角。

2.三角形的内角和为180度。

3.三角形的边可以分为等边三角形、等腰三角形和普通三角形三种情况。

4.等边三角形的三条边都相等，三个内角也都相等，每个内角为60度。

5.等腰三角形的两条边相等，两个相等的内角也相等。

6.普通三角形的三条边和三个内角都不相等。

7.直角三角形有一个直角，即一个内角为90度。

8.钝角三角形有一个钝角，即一个内角大于90度。

9.锐角三角形的三个内角都小于90度。

二、性质1.等边三角形的高同时也是它的中线和角平分线，且它可以由等腰直角三角形通过旋转得到。

2.等腰三角形的高、中线和角平分线都相等且重合，且它可以由等边三角形通过拉伸得到。

3.直角三角形的两个直角边的平方和等于斜边的平方，即勾股定理。

4.三角形的高是从一个内角所在顶点到对边的垂线段，将三角形分为两个三角形，其面积等于底乘以高再除以25.三角形两边夹角内的内角和等于它的对角外的内角。

6.三角形两个等边对应内角相等，两个等腰对应内角相等。

7.如果一个三角形的两个角分别等于另一个三角形的两个角，则这两个三角形相似。

8.如果两个三角形的对应边成比例，则这两个三角形相似。

9.如果两个三角形的对应边成比例且一个对应角相等，则这两个三角形相似。

三、判断题1.一个三角形的三个内角都小于90度，则它是一个锐角三角形。

√2.一个三角形的两个内角相等，则它是一个等腰三角形。

√3.一个三角形的三个内角和等于180度。

√4.一个三角形的两个内角相加小于90度，则它是一个钝角三角形。

√5.一个三角形的三条边都相等，则它是一个等腰直角三角形。

√四、计算题1. 已知一个等边三角形的周长为18cm，求它的边长。

解：因为等边三角形的三条边相等，所以周长18cm除以3，得到每条边的长度为6cm。

答: 6cm。

2. 已知一个等腰三角形的底边长度为10cm，等腰边长是底边的2倍，求它的周长。

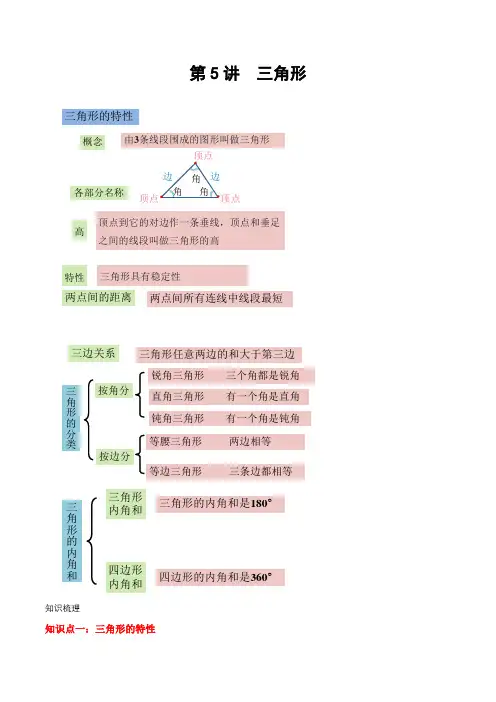
第5讲 三角形三角形的特性概念由3条线段围成的图形叫做三角形各部分名称顶点顶点顶点边边角角角高特性顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高三角形具有稳定性两点间的距离三边关系两点间所有连线中线段最短三角形任意两边的和大于第三边三角形的分类三角形的内角和三角形的内角和是180°三角形内角和四边形内角和四边形的内角和是360°知识梳理知识点一：三角形的特性1. 由3条线段围成的图形（每相邻两条线段的端点相连）叫做三角形。

从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高。

这条对边叫做三角形的底。

三角形ABC ，具有稳定性。

2.三角形三边关系三角形任意两边的和大于第三边。

知识点二：三角形的分类 1.按角进行分类1个直角2个锐角1个钝角2个锐角直角三角形钝角三角形锐角三角形3个锐角：2. 按边进行分类三条边相等两条边相等三条边都不等等边三角形（正三角形）等腰三角形知识点三：三角形的内角和考点一：三角形的特性例1．（2019春•沛县月考）一个等腰三角形两条边的长度分别是5厘米和11厘米，这样的三角形有几个？周长是多少厘米？【分析】根据三角形三边的关系：两边之和大于第三条边，一个等腰三角形两条边的长度分别是5厘米和11厘米，只有一种情况：腰为11厘米，底为5厘米时，周长为11+11+5厘米．【解答】解：根据分析，这个等腰三角形的周长为：11+11+5＝27（厘米）答：有一个这样的三角形，周长分别为27厘米．【点评】此题关键利用三角形三边的关系，再根据三角形周长的计算方法，列式解答即可．1．（2019春•明光市期末）一个三角形的两边长分别是6厘米和9厘米，第三条边的长度一定大于3厘米，同时小于15厘米．【分析】根据三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边；进行解答即可．【解答】解：9﹣6＜第三边＜9+6，即3＜第三边＜15．故答案为：3；15．【点评】解答此题的关键是根据三角形的特性进行分析、解答即可．2．（2018春•厦门期末）王老师给同学们准备了一些小棒，数量如图．选用其中的部分小棒搭成一个长方体．（1）长方体一共有12条棱，每组相对的棱有4条，因此，不可能选用8cm的小棒．（2）这个长方体相交于一个顶点的三条棱的长度分别是5cm、4cm和4cm．（3）计算这个长方体的表面积．【分析】（1）（2）根据长方体的特征即可求解；（3）根据长方体的表面积公式：S＝（ab+ah+bh）×2，把数据代入公式解答即可．【解答】解：（1）长方体一共有12条棱，每组相对的棱有4条，因此，不可能选用8cm的小棒．（2）这个长方体相交于一个顶点的三条棱的长度分别是5cm、4cm和4cm．（3）（5×4+5×4+4×4）×2＝（20+20+16）×2＝56×2＝112（平方厘米）答：这个长方体的表面积是112平方厘米．故答案为：12，4，8；5，4，4．【点评】此题主要考查长方体的表面积公式的灵活运用，关键是熟记公式．3．（2018春•射阳县月考）把一根12厘米的吸管剪成3段（每段都是整厘米数），摆成一个三角形，共有几种剪法，你能全部列举出来吗？【分析】根据三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边；进行解答即可．【解答】解：三角形的特性：两边之和大于第三边，三角形的两边的差一定小于第三边，且12＝3+4+5＝4+4+4＝2+5+5，符合题意的三角形各边分别为：①3、4、5；②4、4、4；③2、5、5；所以共有3种剪法，可以是3、4、5；4、4、4；2、5、5．【点评】围成三角形中任意两条边的和大于第三边，即最长边要小于总长度的一半，是判断三条线段能否围成一个三角形的关键．考点二：三角形的分类例2．（2020春•灯塔市期末）在点子图上按要求画图．【分析】根据平行四边形、梯形、直角三角形、等腰三角形的定义以及它们的特征，即可画图，因为没有规定的确切数据，所以此题答案不唯一．【解答】解：【点评】此题主要考查了常见的几种简单图形的定义以及画法．1．（2019春•肇州县校级期末）分一分，将正确答案的序号填在括号内．【分析】根据三角形按照角的大小分类情况，三角形按照角的大小分为锐角三角形、直角三角形、钝角三角形．三个角都是锐角的三角形叫做锐角三角形；有一个角等于90°的三角形叫做直角三角形；有一个角是钝角的三角形叫做钝角三角形；据此进行判断即可．【解答】解：锐角三角形：①④⑦直角三角形：②⑧钝角三角形：③⑤⑥故答案为：【点评】此题考查的目的是理解掌握三角形按照角的大小分类的情况及应用，要熟悉各类三角形的判定条件．2．（2018秋•醴陵市期末）（探究题）两个椭圆圈重合的部分应是什么三角形？【分析】有两个角相等的直角三角形是等腰直角三角形，据此解答．【解答】解：有两个角相等的直角三角形是等腰直角三角形；所以两个椭圆圈重合的部分应是等腰直角三角形．答：两个椭圆圈重合的部分应是等腰直角三角形．【点评】掌握等腰直角三角形的特点是解题的关键．3．（2016春•岑溪市期中）下面3个三角形被盖住了一个或两个角，你能知道各是什么三角形吗？【分析】根据三角形按角分类的特征可知，三个角都是锐角，这个三角形是锐角三角形；有一个角是钝角的三角形是钝角三角形；有一个角是直角的三角形是直角三角形，解答即可．【解答】解：观图可知：第一个三角形有一个角是直角，所以是直角三角形，第二个三角形有一个角是钝角，所以是钝角三角形第三个三角形有2个角是锐角，所以有可能是锐角三角形，也可能是钝角三角形和直角三角形；故答案为：．【点评】正确理解锐角三角形、直角三角形和钝角三角形的定义是解决此题的关键．考点三：三角形的内角和例3．（2020春•铁西区期末）写出下面∠C的度数．【分析】根据三角形内角和为180°，用内角和减去其余两个角的度数即可求出∠C的度数。

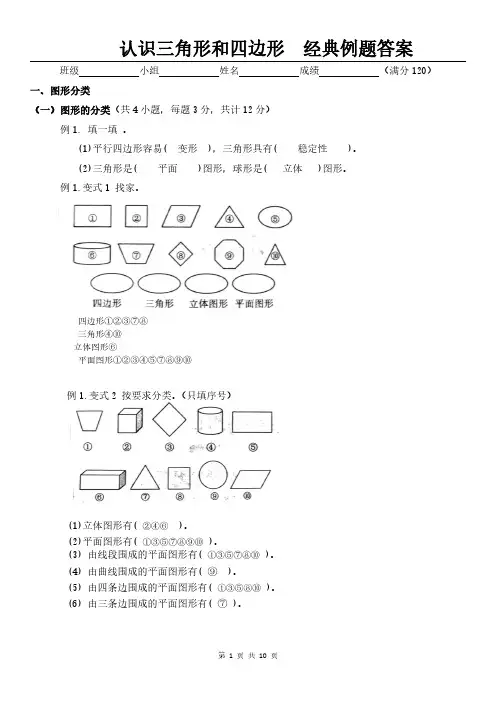
人教版四年级数学下册第5单元《三角形》知识点梳理一、三角形的特性1.三角形的定义。

由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。

2.三角形的各部分的名称。

三角形有3条边,3个顶点,3个角。

3.三角形的表示方法。

为了表达方便,可以用字母A、B、C分别表示三角形的3个顶点,下面的三角形可以表示成三角形ABC。

4.三角形的高。

定义:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。

(如右图)画法:注意:锐角三角形的3条高都在三角形的里面。

钝角三角形有一条高在三角形的里面,2条高在三角形的外面。

(如图)直角三角形的两条直角边是互相垂直的,互为底和高。

(如下图所示)5.三角形的特性。

三角形具有稳定性。

6.两点间的距离。

两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。

7.三角形3条边的关系。

三角形任意两边之和大于第三边。

二、三角形的分类1.用集合圈表示三角形的分类。

2.特殊三角形的特点。

等腰三角形:相等的两条边叫做三角形的腰,两腰与底边的夹角叫做底角。

等腰三角形的两腰相等,两个底角也相等。

等边三角形:等边三角形也叫做正三角形。

3条边都相等,3个角也相等,都是60°。

直角三角形:直角三角形中相互垂直的两条边叫做直角边,直角所对的边叫做斜边,斜边大于任意一条直角边。

一个三角形中最少有2个锐角。

等边三角形是特殊的等腰三角形,但等腰三角形不一定是等边三角形。

三、三角形的内角和1.三角形的内角和是180°。

2.三角形内角和的应用:在一个三角形中,已知两个角的度数,可以根据“三角形的内角和是180°”求出第三个角的度数。

典型题目:一个等腰三角形的一个内角是70°,另外两个角分别是多少度?分析:不知道70°的角是顶角还是底角,所以此题有两种可能。

解答:(180°-70°)÷2=55°或180°-70°×2=40°答:另外两个角可能都是55°,也可能一个是70°,一个是40°。

认识三角形和四边形经典例题答案班级小组姓名成绩（满分120）一、图形分类（一）图形的分类（共4小题，每题3分，共计12分）例1.填一填。

(1)平行四边形容易(变形)，三角形具有(稳定性)。

(2)三角形是(平面)图形，球形是(立体)图形。

例1.变式1找家。

四边形①②③⑦⑧三角形④⑩立体图形⑥平面图形①②③④⑤⑦⑧⑨⑩例1.变式2按要求分类。

（只填序号）(1)立体图形有(②④⑥)。

(2)平面图形有(①③⑤⑦⑧⑨⑩)。

(3)由线段围成的平面图形有(①③⑤⑦⑧⑩)。

(4)由曲线围成的平面图形有(⑨)。

(5)由四条边围成的平面图形有(①③⑤⑧⑩)。

(6)由三条边围成的平面图形有(⑦)。

例1.变式3哪种围篱笆的方法更牢固？为什么？答：第二种方法更牢固，利用了三角形的稳定性（二）理解三角形的稳定性和四边形的不稳定性及其在生活中的运用（共4小题，每题3分，共计12分）例2.观察下面物体，你发现了什么？答：发现生活中的物品都是由图形构成的，三角形能起到很好的固定作用例2.变式1数一数，下面图中各有几个三角形。

104例2.变式2从一块长方形木板上锯掉一块宽为20厘米的长方形木条，剩下的木板为一个正方形，周长为180厘米，求原来长方形木板的周长和锯下的长方形木条的周长。

原：（180÷4+20+180÷4）×2=220（厘米）锯：（20+180÷4）×2＝130（厘米）答：原来长方形木板的周长是220厘米，锯下的长方形木条的周长是130厘米.例2.变式3自行车的三角形车架是利用了三角形的（稳定性）特性.例3.填一填。

(1)三个角都是(锐)角的三角形是锐角三角形，有(一)个角是(直角)的三角形是直角三角形，有(一)个角是(钝角)的三角形是钝角三角形。

(2)有(两)条边相等的三角形是等腰三角形，(三)条边都相等的三角形是等边三角形。

例3.变式1分类。

(1)锐角三角形有(①⑤⑥)。

小学数学三角形的分类与性质知识点说起三角形，这可是咱小学数学里相当重要的一块儿内容呢！想当年，我在学习三角形的时候，那可是经历了不少有趣的事儿。

先来说说三角形的分类吧。

三角形按照角的大小，可以分成锐角三角形、直角三角形和钝角三角形。

锐角三角形，顾名思义，就是三个角都小于 90 度的三角形。

那时候，老师为了让我们搞清楚这个概念，可费了不少心思。

记得有一次上课，老师拿着一个大大的三角板，在黑板上画了各种三角形，然后指着其中一个角问我们：“同学们，这个角是锐角、直角还是钝角呀？”大家都瞪大眼睛，仔细观察着。

我当时心里还挺紧张的，生怕答错了。

当老师公布答案的时候，我发现自己答对了，心里那叫一个美！直角三角形就更好理解啦，它有一个角正好是 90 度，就像那个直角三角板一样。

老师还特意让我们回家找一找生活中哪些东西是直角三角形的形状。

我回到家，东瞅瞅西看看，嘿，还真让我发现了不少！比如我家的那个折叠小凳子，撑开的时候，其中的支架就是直角三角形的。

还有我爸的工具箱里，有一个直角尺，那也是标准的直角三角形。

钝角三角形呢，就是有一个角大于 90 度小于 180 度的三角形。

这个可有点难想象，不过老师给我们举了个例子，说就像那种老式的大扇子，打开的时候，扇骨和扇面组成的形状就可能是钝角三角形。

三角形按照边的长短来分，又可以分成等边三角形、等腰三角形和一般三角形。

等边三角形可特别了，三条边都一样长。

那时候，我们做手工，老师让我们用小木棍来搭等边三角形。

我一开始总是搭不好，不是这边长了，就是那边短了。

后来，我仔细比对每根小木棍的长度，终于搭出了一个完美的等边三角形，那种成就感，真的没法形容！等腰三角形呢，就是有两条边相等的三角形。

老师为了让我们记住这个特点，还让我们在纸上画等腰三角形，然后用剪刀剪下来。

我剪的时候可小心了，就怕把边剪歪了。

剪完之后，我拿着自己的等腰三角形，左看看右看看，觉得特别有意思。

说完了分类，再来说说三角形的性质。

三角形一、三角形的特征1、三角形的定义、高、底边、角由三条线段围成的图形（每相邻的条线段的端点相连）叫做三角形。

三角形的表示方法。

三角形可以用字母表示，成三角形ABC。

从三角形的一个顶点到它的对边做一条垂线，顶点和垂足之间的线段叫做三角形的高。

2、关于三角形的高例1、下图中，AC边上高的画法正确的是（）。

练习：根据下面每个图形标出的底，画出图形的高。

底底底3、数三角形的个数。

例1、下图中有（）个三角形练习：下图中有（）个三角形4、三角形的特性三角形具有稳定性，并在生活中被广泛应用。

举例说明生活中的应用。

二、三角形的分类1、三角形按角分类三角形可以分为锐角三角形，直角三角形和钝角三角形。

因为在一个三角形至少有两个锐角，所以可以直角根据最大的角判断三角形的类型，最大的角是哪类角。

例1、将下图分成三个三角形，它们可能是什么三角形？你能想出哪些有分法？例2、仔细填下列图。

三角形的分类锐角三角形直角三角形钝角三角形锐角的个数直角的个数钝角的个数1、一个三角形里面最多有（）锐角，最少有（）个锐角。

A、1B、2C、32、一个直角三角形中，最多有（）个锐角。

A、1B、2C、33、在一个三角形中，有两个角都是60°，这是（）三角形。

A、等边B、等腰C、直角4、如右图，一块三角形纸片被撕去了一个角。

这个角是（）度，原来这块纸片的形状是（）三角形，也是（）三角形。

2、三角形的内角和180°（证明）例1、求出下面图形中的角的度数。

例2、一个等腰三角形的顶角是底角的4倍，这个等腰三角形的底角和顶角分别是多少度？练习、1、求下面各角的度数,并指出它们是什么三角形？（1）∠1=42°，∠2=38°，求∠3的度数。

（2）∠1=28°，∠2=62°，求∠3的度数。

（3）∠1=48°，∠2=62°，求∠3的度数。

总结：对于任意一个三角形，至少都有两个锐角。

四年级下数学《三角形的分类、特征》知识点总结与归纳一、知识点梳理1.三角形的定义：由三条边和三个角围成的封闭图形。

2.三角形的基本性质：•稳定性：三角形具有稳定性，不易变形。

•内角和定理：三角形的内角和等于180度。

•边角关系：三角形的两边之和大于第三边，两边之差小于第三边。

1.三角形的分类方法：•按角度分类：锐角三角形（所有角都小于90度）、直角三角形（有一个角等于90度）、钝角三角形（有一个角大于90度）。

•按边分类：等边三角形（三边相等）、等腰三角形（两边相等）、不等边三角形（三边都不等）。

1.各类三角形的特征：•锐角三角形：所有角都小于90度，相对较“瘦”。

•直角三角形：有一个角等于90度，相对较“方”。

•钝角三角形：有一个角大于90度，相对较“胖”。

•等边三角形：三边相等，三个角都等于60度。

•等腰三角形：两边相等，两腰之间的角度相等。

1.三角形的边与角的关系：•在同一个三角形中，角度相等的两边之和大于第三边。

•在同一个三角形中，边长相等的两个角之和等于第三个角的补角。

二、公式及定理1.内角和定理：三角形的内角和等于180度。

2.边角关系定理：在同一个三角形中，角度相等的两边之和大于第三边；边长相等的两个角之和等于第三个角的补角。

3.三角形的面积公式：面积= (底× 高) ÷ 2。

4.等边三角形的性质定理：等边三角形的三个内角都等于60度。

5.等腰三角形的性质定理：等腰三角形的两腰之间的角度相等。

三、解题方法与技巧1.根据三角形的特征判断类型：通过观察三角形的角度或边的长度，判断其属于哪种类型的三角形。

2.利用三角形的内角和定理求角度：已知三角形的两个角度，可以通过内角和定理求第三个角度。

3.利用三角形的边角关系判断能否构成三角形：判断三条线段能否构成三角形，可以根据三角形的边角关系进行判断。

4.利用等腰三角形和等边三角形的性质简化计算：在解题过程中，如果遇到等腰三角形或等边三角形，可以利用它们的性质简化计算。

三角形基础知识及习题三角形是几何学中最基本的图形之一，其基础知识对于学习几何学和解决几何问题至关重要。

本文将介绍三角形的基本定义、分类和性质，并提供一些习题供读者练习。

一、三角形的定义和分类1. 定义：三角形是由三条线段（边）所围成的图形。

三角形的三个顶点（角）和三个边缘（边）都相互连接。

2. 分类：根据三个角的大小，三角形可以分为三种类型：a. 锐角三角形：三个角都小于90度。

b. 直角三角形：其中一个角为90度。

c. 钝角三角形：其中一个角大于90度。

二、三角形的性质1. 角度和：三角形的三个角的角度和总是等于180度。

无论三角形是锐角、直角还是钝角三角形，其内角之和都是180度。

2. 边长关系：a. 等边三角形：三个边的长度都相等。

b. 等腰三角形：两个边的长度相等。

c. 直角三角形：满足毕达哥拉斯定理，即两直角边的平方和等于斜边的平方。

3. 角度关系：a. 锐角三角形：三个角都是锐角。

b. 直角三角形：其中一个角是直角。

c. 钝角三角形：其中一个角是钝角。

三、三角形的习题下面是几个关于三角形的习题，供读者练习运用三角形的基础知识与技巧。

1. 题目：已知三角形的两边长分别为5厘米和8厘米，夹角为60度，求第三条边的长度。

解法：利用余弦定理，可以得到第三条边的长度：c^2 = a^2 + b^2 - 2abcosC。

带入数值计算得到c≈7.53厘米。

2. 题目：在直角三角形ABC中，AB = 3厘米，BC = 4厘米，求AC的长度。

解法：根据毕达哥拉斯定理，可以得到AC的长度：AC^2 =AB^2 + BC^2。

带入数值计算得到AC = 5厘米。

3. 题目：已知三角形的两边长分别为6厘米和8厘米，以及夹角为30度，求第三条边的长度。

解法：利用正弦定理，可以得到第三条边的长度：a/sinA = b/sinB = c/sinC。

带入数值计算得到第三条边的长度约为7.61厘米。

4. 题目：在锐角三角形ABC中，AB = 7厘米，BC = 9厘米，夹角为45度，求角度C的大小。

第七章三角形【知识要点】一．认识三角形1．关于三角形的概念及其按角的分类定义：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

2．三角形的分类：①三角形按内角的大小分为三类：锐角三角形、直角三角形、钝角三角形。

②三角形按边分为两类：等腰三角形和不等边三角形。

2．关于三角形三条边的关系（判断三条线段能否构成三角形的方法、比较线段的长短）根据公理“两点之间，线段最短”可得：三角形任意两边之和大于第三边。

三角形任意两边之差小于第三边。

3．与三角形有关的线段．．：三角形的角平分线、中线和高三角形的角平分线：三角形的一个角的平分线与对边相交形成的线段；三角形的中线：连接三角形的一个顶点与对边中点的线段，三角形任意一条中线将三角形分成面积相等的两个部分；三角形的高：过三角形的一个顶点做对边的垂线，这条垂线段叫做三角形的高。

注意：①三角形的角平分线、中线和高都是线段，不是直线，也不是射线；②任意一个三角形都有三条角平分线，三条中线和三条高；③任意一个三角形的三条角平分线、三条中线都在三角形的内部。

但三角形的高却有不同的位置：锐角三角形的三条高都在三角形的内部；直角三角形有一条高在三角形的内部，另两条高恰好是它两条直角边；钝角三角形一条高在三角形的内部，另两条高在三角形的外部。

④一个三角形中，三条中线交于一点，三条角平分线交于一点，三条高所在的直线交于一点。

（三角形的三条高（或三条高所在的直线）交与一点，锐角三角形高的交点在三角形的内部，直角三角形高的交点是直角顶点，钝角三角形高（所在的直线）的交点在三角形的外部。

）4．三角形的内角与外角（1）三角形的内角和：180°引申：①直角三角形的两个锐角互余；②一个三角形中至多有一个直角或一个钝角；③一个三角中至少有两个内角是锐角。

（2）三角形的外角和：360°（3）三角形外角的性质：①三角形的一个外角等于与它不相邻的两个内角的和；——常用来求角度②三角形的一个外角大于任何一个与它不相邻的内角。

第七章三角形【知识要点】一．认识三角形1．关于三角形的概念及其按角的分类定义：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

2．三角形的分类：①三角形按内角的大小分为三类：锐角三角形、直角三角形、钝角三角形。

②三角形按边分为两类：等腰三角形和不等边三角形。

2．关于三角形三条边的关系（判断三条线段能否构成三角形的方法、比较线段的长短）根据公理“两点之间，线段最短”可得：三角形任意两边之和大于第三边。

三角形任意两边之差小于第三边。

3．与三角形有关的线段．．：三角形的角平分线、中线和高三角形的角平分线：三角形的一个角的平分线与对边相交形成的线段；三角形的中线：连接三角形的一个顶点与对边中点的线段，三角形任意一条中线将三角形分成面积相等的两个部分；三角形的高：过三角形的一个顶点做对边的垂线，这条垂线段叫做三角形的高。

注意：①三角形的角平分线、中线和高都是线段，不是直线，也不是射线；②任意一个三角形都有三条角平分线，三条中线和三条高；③任意一个三角形的三条角平分线、三条中线都在三角形的内部。

但三角形的高却有不同的位置：锐角三角形的三条高都在三角形的内部；直角三角形有一条高在三角形的内部，另两条高恰好是它两条直角边；钝角三角形一条高在三角形的内部，另两条高在三角形的外部。

④一个三角形中，三条中线交于一点，三条角平分线交于一点，三条高所在的直线交于一点。

（三角形的三条高（或三条高所在的直线）交与一点，锐角三角形高的交点在三角形的内部，直角三角形高的交点是直角顶点，钝角三角形高（所在的直线）的交点在三角形的外部。

）4．三角形的内角与外角（1）三角形的内角和：180°引申：①直角三角形的两个锐角互余；②一个三角形中至多有一个直角或一个钝角；③一个三角中至少有两个内角是锐角。

（2）三角形的外角和：360°（3）三角形外角的性质：①三角形的一个外角等于与它不相邻的两个内角的和；——常用来求角度②三角形的一个外角大于任何一个与它不相邻的内角。

分类三角形的题目
以下就是小编给大家盘点的分类三角形的题目，仅供大家参考。

三角形的分类有很多种方法，以下是常见的两种分类方式及相关题目：
一、按角分类
1、锐角三角形：三个角都是锐角的三角形。

2、直角三角形：有一个角是直角的三角形。

3、钝角三角形：有一个角是钝角的三角形。

相关题目：
判断下列三角形属于哪一类：
1、三角形的三个角分别为30°、60°、90°。

（直角三角形）
2、三角形的三个角分别为80°、50°、50°。

（锐角三角形）
二.按边分
1、等边三角形：三条边都相等的三角形。

2、等腰三角形：至少有两条边相等的三角形。

3、不等边三角形：三条边都不相等的三角形。

相关题目：
下列三角形中，一定是等边三角形的是（）。

A.有两个角是60°的三角形
B.三个角都相等的三角形
C.有一个角是60°的等腰三角形
答案选B。

根据等边三角形的判定定理：三个角都相等的三角形是等边三角形，可得选项B正确；而选项A和选项C只是满足等边三角形的其中一个条件，不能确定该三角形一定是等边三角形。

以上是关于三角形分类的两种常见方式及相关题目示例，希望对你有所帮助！。

三角形的分类三角形是由三条线段所围成的图形，其中每条线段称为三角形的边，每两条边所形成的交点称为三角形的顶点。

根据三角形的边长和角度的不同，我们可以将三角形进行分类。

本文将详细介绍三角形的分类，包括等边三角形、等腰三角形、直角三角形、锐角三角形、钝角三角形和等腰直角三角形。

一、等边三角形等边三角形是指三条边都相等的三角形。

在等边三角形中，每个内角都是60度。

等边三角形的性质包括：三条中线相等，三条高相等，三条角平分线相等，内切圆和外接圆半径相等。

二、等腰三角形等腰三角形是指有两条边相等的三角形。

在等腰三角形中，两个底角相等，顶角等于180度减去两个底角的和。

等腰三角形的性质包括：两条中线相等，两条高相等，两条角平分线相等。

三、直角三角形直角三角形是指其中一个内角是90度的三角形。

在直角三角形中，其余两个内角必须是锐角或钝角。

直角三角形的性质包括：勾股定理，即直角三角形两条直角边的平方和等于斜边的平方。

四、锐角三角形锐角三角形是指三个内角都是锐角（小于90度）的三角形。

锐角三角形的性质包括：三个内角的和等于180度，最长边对应最大的内角。

五、钝角三角形钝角三角形是指其中一个内角是钝角（大于90度）的三角形。

钝角三角形的性质包括：三个内角的和等于180度，最长边对应最大的内角。

六、等腰直角三角形等腰直角三角形是指既是等腰三角形又是直角三角形的三角形。

在等腰直角三角形中，两个腰长相等，底边是腰长的根号二倍。

等腰直角三角形的性质包括：勾股定理，两条中线相等，两条高相等，两条角平分线相等。

三角形可以根据边长和角度的不同进行分类，包括等边三角形、等腰三角形、直角三角形、锐角三角形、钝角三角形和等腰直角三角形。

每种三角形都有其独特的性质和特点。

通过对三角形的分类，我们可以更好地理解和应用三角形的性质和定理。

在上述分类中，直角三角形是一个需要重点关注的类别，因为它具有独特的性质和应用，特别是在数学和物理学中。

直角三角形的一个著名性质是勾股定理，它描述了直角三角形两条直角边与斜边之间的关系。

三角形一、三角形的特征及分类1、围成三角形的条件：两边之和大于第三边。

2、从三角形的一个顶点到对边的垂直线段是三角形的高，这条对边是三角形的底。

3、三角形具有稳定性（也就是当一个三角形的三条边的长度确定后，这个三角形的形状和大小都不会改变），生活中很多物体利用了这样的特性。

如：人字梁、斜拉桥、自行车车架。

4、三个角都是锐角的三角形是锐角三角形。

（两个内角的和大于第三个内角。

）5、有一个角是直角的三角形是直角三角形。

（两个内角的和等于第三个内角。

两个锐角的和是90度。

两条直角边互为底和高。

）6、有一个角是钝角的三角形是钝角三角形。

（两个内角的和小于第三个内角。

）7、任意一个三角形至少有两个锐角，都有三条高，三角形（锐角三角形的三条高都在三角形内；的内角和都是180度。

直角三角形有两条高落在两条直角边上；钝角三角形有两条高在三角形外）。

8、把一个三角形分成两个直角三角形就是画它的高。

二、三角形内角和、等腰三角形、等边三角形1、两条边相等的三角形是等腰三角形，相等的两条边叫做腰，另外一条边叫做底，两条腰的夹角叫做顶角，底和腰的两个夹角叫做底角，它的两个底角也相等，是轴对称图形，有一条对称轴（跟底边高正好重合。

）三条边都相等的三角形是等边三角形，三条边都相等，三个角也都相等（每个角都是60°，所有等边三角形的三个角都是60°。

）2、有一个角是直角的等腰三角形叫做等腰直角三角形，它的底角等于45°，顶角等于90°。

3、求三角形的一个角=180°－另外两角的和4、等腰三角形的顶角=180°－底角×2=180°－底角－底角5、等腰三角形的底角=（180°－顶角）÷26、一个三角形最大的角是60度，这个三角形一定是等边三角形。

7、多边形的内角和=180°×（n－2）{n为边数}平行四边形和梯形一、认识平行四边形1、两组对边互相平行的四边形叫平行四边形，它的对边平行且相等，对角相等。

四年级数学三角形知识点归纳只要大家脚踏实地的复习，一定能够提高数学应用能力!希望小编为大家准备的四年级数学三角形知识点，对大家有所帮助!四年级数学三角形知识点归纳等腰三角形中，两腰相交于一点形成的夹角是顶角;两腰与底相交形成的两个夹角是底角。

接下来，和小编一起来看一下四年级数学三角形知识点。

1.由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。

2.三角形有3条边，3个角，3个顶点。

3.从三角形的一个顶点到它的对边做一条垂线，顶点和垂足之间的线段叫做三角形的高，这条对边叫做三角形的底。

4.三角形有3条高，3个底。

5.三角形具有稳定性，不易变形。

6.三角形任意两边的和大于第三边。

7.三角形任意两边的差小于第三边。

8.快速判断任意三条线段能否围成一个三角形：看两条较短的线段之和是否大于第三条线段。

9.直角三角形的两条直角边互为底和高。

10.三个角都是锐角的三角形，是锐角三角形。

11.有一个直角的三角形，是直角三角形。

12.有一个钝角的三角形，是钝角三角形。

13.三角形按角分：锐角三角形、直角三角形、钝角三角形13.三角形按边分：普通三角形、等腰三角形、等边三角形14.有两条边相等的三角形是等腰三角形。

(按边)有两个角相等的三角形是等腰三角形。

(按角)15.有三条边相等的三角形是等边三角形。

(按边)有三个角相等的三角形是等边三角形。

(按角)注：课本83页三角形集合图。

16.等边三角形是特殊的等腰三角形。

17.等边三角形一定是锐角三角形。

18.等腰三角形的两腰相等，两个底角相等。

19.等边三角形的三条边相等，三个角也相等，都是60度。

20.等边三角形也叫正三角形。

21.等腰三角形中，两腰相交于一点形成的夹角是顶角;两腰与底相交形成的两个夹角是底角。

(P84图)22.三角形的内角和是180度。

23.多边形的内角和=180度×(多边形的边数-2)24.任意一个四边形的内角和是360度。

25.两个完全一样的三角形可以拼成三角形、正方形、长方形、平行四边形、和四边形。