采用矩形法求定积分

C语言用六种方法求定积分C语言中求定积分的方法主要有以下六种：基本公式法、数值积分法、Laplace变换法、微积分概念法、数值积分法和Monte Carlo方法。

下面将详细介绍每种方法的原理和实现。

1.基本公式法：基本公式法是求解定积分的最基本方法，根据不同函数的特点和性质，利用已知的积分公式进行求解。

例如，对于一次函数和常数函数，可以使用基本公式法求解。

2.数值积分法：数值积分法是通过将定积分转化为数值计算问题来求解。

常用的数值积分方法有矩形法、梯形法和辛普森法等。

这些方法基于将求积分区间分割成若干个小区间，然后在每个小区间上近似计算出函数的积分值，再将这些积分值加总得到最终结果。

3. Laplace变换法：Laplace变换法是一种利用Laplace变换求解微分方程的方法，也可以用来求解定积分。

通过将被积函数进行Laplace变换，然后利用Laplace变换公式求解积分，最后再求出反变换得到结果。

4.微积分概念法：微积分概念法是通过将定积分定义为函数曲线下的面积来求解。

具体做法是将被积函数图像与坐标轴围成的面积分为若干个小的矩形、梯形或曲线段以及一个小的区域。

然后根据图形的几何性质进行近似计算，将这些小面积相加得到最终结果。

5.数值积分法：数值积分法也是一种基于数值计算的方法，但与前面提到的数值积分法不同，它通过构造一系列特定形式的插值函数对被积函数进行逼近，然后计算插值函数的积分值来近似求解定积分。

常用的数值积分法有牛顿-科特斯公式和高斯-勒让德公式。

6. Monte Carlo方法：Monte Carlo方法是一种基于统计随机性的数值积分方法，它通过随机抽样来进行数值求解。

具体做法是在被积函数图像下随机抽取一系列点，根据这些随机点的坐标和函数值来估计函数的积分值。

通过对多次随机抽样的结果取平均可以得到定积分的近似值。

以上六种方法都可以用C语言来实现，具体的实现方法可以根据具体问题的特点和要求选择合适的算法和数据结构，然后编写相应的代码实现。

第9章过程9.1 Sub过程9.1.1建立Sub过程1. 定义Sub过程2VisualBasic程序设计教程(第三版)2. 建立Sub过程图9.1“添加过程”对话框图9.2模块代码窗口9.1.2调用Sub过程1. 用Call语句调用Sub过程2. 把过程名作为一个语句来使用VisualBasic程序设计教程(第三版) 3图9.3时间延迟4VisualBasic程序设计教程(第三版) 9.1.3通用过程与事件过程VisualBasic程序设计教程(第三版) 56VisualBasic程序设计教程(第三版) 9.2 Function过程9.2.1建立Function过程VisualBasic程序设计教程(第三版) 7 9.2.2调用Function过程图9.4输出随机数8VisualBasic程序设计教程(第三版)图9.5求平方根VisualBasic程序设计教程(第三版) 9图9.6 Visual Basic应用程序中的过程9.3参数传送9.3.1形参与实参1. 按位置传送图9.7形参与实参2. 指名传送10VisualBasic程序设计教程(第三版) 9.3.2引用图9.8过程的副作用9.3.3传值9.3.4数组参数的传送图9.9实参数组与形参数组图9.10用梯形法求定积分图9.11求定积分（界面设计）图9.12求定积分（求值结果）9.4可选参数与可变参数9.4.1可选参数9.4.2可变参数9.5对象参数9.5.1窗体参数9.5.2控件参数图9.13控件参数示例图9.14 TypeOf 语句示例图9.15控件移动（界面设计）图9.16控件移动（运行情况）9.6局部内存分配9.7递归图9.17递归调用操作习题9.1编写一个求3个数中最大值Max和最小值Min的过程，然后用这个过程分别求3个数和5个数、7个数中的最大值和最小值。

9.2编写程序，求S=A!+B!+C!，阶乘的计算分别用Sub过程和Function过程两种方法来实现。

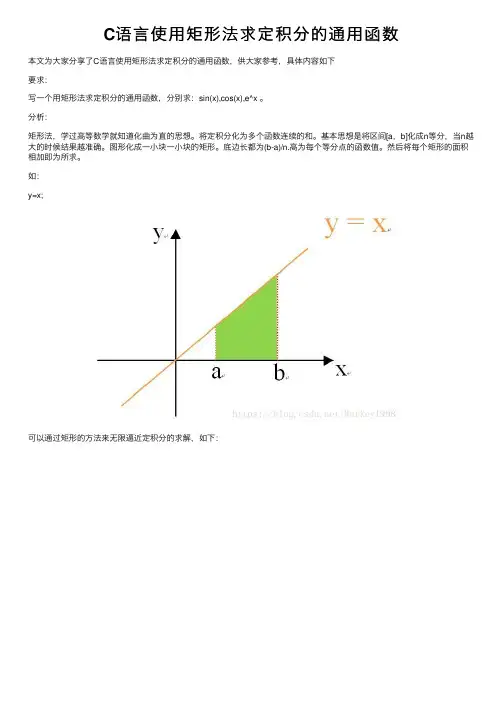
C语⾔使⽤矩形法求定积分的通⽤函数本⽂为⼤家分享了C语⾔使⽤矩形法求定积分的通⽤函数，供⼤家参考，具体内容如下要求：写⼀个⽤矩形法求定积分的通⽤函数，分别求：sin(x),cos(x),e^x 。

分析：矩形法，学过⾼等数学就知道化曲为直的思想。

将定积分化为多个函数连续的和。

基本思想是将区间[a，b]化成n等分，当n越⼤的时候结果越准确。

图形化成⼀⼩块⼀⼩块的矩形。

底边长都为(b-a)/n.⾼为每个等分点的函数值。

然后将每个矩形的⾯积相加即为所求。

如：y=x;可以通过矩形的⽅法来⽆限逼近定积分的求解，如下：因为被分成n等分，就可以认为每⼀等分是⼀个矩形，那么每⼀矩形的⾯积为：每⼀个矩形⾯积为：***Sn=f(x)(b-a)/n 总⾯积为：****S=S1+S2+…+Sn#include <stdio.h>#include <stdlib.h>#include <math.h>//引⼊sin x,cos x,e^x的库//使⽤指向函数的指针变量来复⽤⼀个通⽤函数int main(){int i,j,k,n,m;float res;float (*fun)(float);//定义指向函数的指针变量float integral (float a,float b,float (*fun)(float),int n);//n为将积分区间（b-a)分成n等分，当n的值越⼤的时候结果越精确，数学上的定义是取⽆穷⼤float fsin(float);//sin x函数的声明float fcos(float);//cos x函数的声明float fexp(float);//e^x 函数的声明printf ("请输⼊积分的下限\n");scanf ("%d",&m);printf ("请输⼊积分的上限\n");scanf ("%d",&n);printf("请输⼊你要计算的函数的具体函数\n");printf("1.sin(x) 2.cos(x) 3.e^x\n");scanf ("%d",&i);switch(i){case 1:fun=fsin;//函数地址（⼊⼝）交给指针变量，灵活性强break;case 2:fun=fcos;break;case 3:fun=fexp;}res=(fun)(2.00);//printf("xxxx=%f\n",res);printf ("计算的结果为\n");res=integral(m,n,fun,200000);printf("res=%f",res);return 0;}float fsin(float x){// printf("fsinx=%f\n",x);return sin(x);}float fcos(float x){//printf("fcosx=%f\n",x);return cos(x);}float fexp(float x){//getchar();//printf("fexp=%f\n",x);return exp(x);}float integral(float a,float b,float (*fun)(float),int n){//矩形法计算,定积分转换为连续求和的形式int i=0;float x=a,s=0;float h=(b-a)/n;for (i=1;i<=n;i++){x=x+h;s=s+((*fun)(x)*h);}return s;}结果：以上就是本⽂的全部内容，希望对⼤家的学习有所帮助，也希望⼤家多多⽀持。

数值积分使用数值方法计算定积分定积分是数学中的重要概念，用于求解曲线下面的面积。

在某些情况下，定积分无法通过解析解来求解，此时可以使用数值方法来进行近似计算。

数值积分是一种广泛应用的技术，本文将介绍数值积分的基本原理以及常见的数值方法。

一、数值积分的基本原理数值积分的基本原理是将曲线下的面积近似为若干个矩形的面积之和。

假设要计算函数f(x)在区间[a, b]上的定积分，首先将[a, b]等分成n个小区间，每个小区间的宽度为Δx=(b-a)/n。

然后，在每个小区间上选择一个代表点xi，计算其对应的函数值f(xi)，然后将所有矩形的面积相加，即可得到近似的定积分值。

二、矩形法矩形法是数值积分中最简单的方法之一。

它将每个小区间上的函数值看作是一个常数，然后通过计算矩形的面积来近似定积分的值。

矩形法主要有两种形式：左矩形法和右矩形法。

1. 左矩形法左矩形法使用小区间左端点的函数值来代表整个小区间上的函数值。

即近似矩形的面积为f(xi) * Δx，其中xi为小区间的左端点。

然后将所有矩形的面积相加，得到近似的定积分值。

2. 右矩形法右矩形法与左矩形法相似，仅仅是使用小区间右端点的函数值来代表整个小区间上的函数值。

近似矩形的面积为f(xi + Δx) * Δx，其中xi为小区间的左端点。

同样地，将所有矩形的面积相加，得到近似的定积分值。

三、梯形法梯形法是比矩形法更精确的数值积分方法。

它通过使用每个小区间的两个端点处函数值的平均值来代表整个小区间上的函数值，并计算梯形的面积来近似定积分的值。

梯形法的计算公式为：(f(xi) + f(xi + Δx)) * Δx / 2，其中xi为小区间的左端点。

将所有梯形的面积相加，得到近似的定积分值。

四、辛普森法辛普森法是一种更加高阶的数值积分方法，它使用三个点对应的函数值来逼近曲线。

将每个小区间看作一个二次函数，可以通过拟合这个二次函数来近似定积分的值。

辛普森法的计算公式为：(f(xi) + 4 * f(xi + Δx/2) + f(xi + Δx)) * Δx / 6，其中xi为小区间的左端点。

定积分的计算与应用定积分是微积分的重要概念之一，用于计算曲线下的面积、质量、体积等问题。

本文将介绍定积分的计算方法和应用场景。

一、定积分的计算方法定积分的计算基于微积分中的积分运算，可以通过以下方法进行计算：1. 几何解释法：定积分可以视为曲线下的面积，因此可以利用几何图形的面积公式进行计算。

将曲线下的区域分割成无数个小矩形，并求取它们的面积之和，即可得到定积分的近似值。

通过增加小矩形的个数，可以不断提高计算精度。

2. 集合解释法：定积分可以被视为一组数的和，其中这组数是将函数值与对应的间隔长度相乘而得到的。

通过将曲线下的区域分割成若干个小区间，并计算每个小区间内的函数值与对应的间隔长度的乘积，再将这些乘积进行加和，即可得到定积分的近似值。

3. 牛顿-莱布尼茨公式：对于可微函数，可以使用牛顿-莱布尼茨公式进行定积分的计算。

该公式表达了函数的原函数（即不定积分）与定积分之间的关系。

通过求取函数的原函数，并在积分的上下限处进行代入计算，即可得到定积分的准确值。

二、定积分的应用场景定积分在物理学、经济学、工程学等领域都有广泛的应用。

以下将介绍一些常见的应用场景：1. 面积计算：最简单的应用是计算平面图形的面积。

通过确定曲线的方程以及积分的上下限，可以计算出曲线所围成区域的面积。

2. 质量计算：如果将曲线下的区域视为物体的密度分布，则可以利用定积分计算物体的质量。

通过将物体分割成无数个小区域，并计算每个小区域内的密度值与对应的区域面积的乘积，再将这些乘积进行加和，即可得到物体的总质量。

3. 体积计算：类似质量计算，定积分可以被用于计算三维物体的体积。

通过将物体分割成无数个小体积，并计算每个小体积的大小，再将这些体积进行加和，即可得到物体的总体积。

4. 概率计算：在概率论中，定积分可以用于计算随机变量的概率密度函数下的概率。

通过计算概率密度函数在某个区间上的定积分，可以得到该区间内事件发生的概率。

5. 积累量计算：定积分还可以用于计算积累量，例如距离、速度、加速度等。

定积分的计算方法定积分是微积分中重要的概念之一，用于计算曲线下面的面积、求函数的平均值等。

在本文中，将介绍一些常见的定积分计算方法，并结合例子进行说明。

1. 定积分的定义定积分可以理解为将一个函数在区间[a, b]上的曲线下方的面积进行求和。

用数学符号表示，可以写作∫[a, b]f(x)dx，其中f(x)是要进行积分的函数，[a, b]表示积分的区间。

2. 几何法几何法是一种简单直观的计算定积分的方法。

它基于几何图形的面积计算方法，通过将曲线下方的区间划分为若干个矩形、梯形或三角形来逼近曲线下方的面积。

例如，我们要计算函数f(x)=x²在区间[0, 1]上的定积分。

首先，将区间[0, 1]平均划分为n个小区间，每个小区间的宽度为Δx=(b-a)/n=(1-0)/n=1/n。

然后，在每个小区间上取一个点xi，并计算出相应的函数值f(xi)。

接着，将矩形的高度设定为f(xi)，则每个小区间上的矩形的面积为f(xi)Δx。

最后，将所有小矩形的面积相加即可得到近似的定积分值。

3. 不定式法不定式法是一种通过求解原函数来计算定积分的方法。

如果给定函数f(x)在[a, b]上连续，并假设F(x)是它的一个原函数，则根据微积分基本定理，可得到∫[a, b]f(x)dx = F(b) - F(a)这意味着我们只需要找到函数f(x)的一个原函数F(x)，并计算F(b)和F(a)的差值，即可求得定积分的值。

举个例子，考虑要计算函数f(x) = x²在区间[1, 3]上的定积分。

首先，求出函数f(x)的一个原函数F(x)。

由f(x) = x²可知，F(x) = (1/3)x³ + C 是f(x)的一个原函数。

根据不定式法，定积分的值为∫[1, 3]x²dx = F(3) - F(1) = (1/3)(3³) + C - [(1/3)(1³) + C] = 9/3 - 1/3 = 8/34. 分部积分法分部积分法是一种利用积分的性质来计算定积分的方法。

求定积分的四种方法在微积分中，确定定积分的值是一个重要的问题。

定积分是一个实函数在给定区间上的积分，表示该函数在该区间上的总体积。

在本文中，我将介绍四种常见的方法来确定定积分的值。

这些方法分别是：几何解释法、Riemann和法、换元积分法和分部积分法。

一、几何解释法例如，如果要计算函数f(x)=x^2在区间[0,1]上的定积分，我们可以将该区间分成无限个小矩形，并计算每个小矩形的面积。

然后将所有小矩形的面积相加，即可得到定积分的值。

对于该例子，我们可以将区间[0,1]分成无限个宽度为dx的小矩形，其高度为f(x)=x^2、因此，定积分的值为∫[0,1]x^2dx=1/3二、Riemann和法Riemann和法是一种将定积分转化为求和的方法。

它使用一个区间分割，把整个区间分成无限个小区间。

然后，通过对每个小区间让其长度趋近于零，计算每个小区间的函数值和相加，从而求得定积分的近似值。

当小区间的数量无限增加时，所得的近似值将趋近于定积分的真正值。

例如，如果要计算函数f(x)=x^2在区间[0,1]上的定积分，我们可以将该区间分成n个小区间，每个区间的宽度为Δx=(1-0)/n，其中n为正整数。

然后，我们可以计算每个小区间的函数值并相加，即可得到定积分的近似值。

当使用Riemann和法时，分割区间的选择对于确定近似值的精确性非常重要。

如果区间分割得足够细，近似值将趋近于定积分的真正值。

三、换元积分法换元积分法是一种通过进行变量替换来简化定积分的方法。

它利用函数的链式法则，将原函数中的自变量替换为新的变量，然后计算新函数的微分。

通过进行适当的变量替换，我们可以将原本复杂的定积分转化为更简单的形式，从而易于计算。

例如，如果要计算函数f(x)=x^2在区间[0,1]上的定积分，我们可以进行变量替换，令u=x^2，则du=2xdx。

通过将原函数中的自变量替换为新变量，我们可以将原本的定积分转化为∫[0,1]u(1/2√u)du。

本科毕业论文定积分的计算方法专业数学与应用数学作者姓名班级2007级1班学号2007011105 指导教师提交日期2011年5月10日陇东学院数学与统计学院2011年5月定积分的计算方法（陇东学院数学与统计学院，甘肃 庆阳 745000）摘 要:本文从定义法,几何意义计算法,公式法以及特殊计算法和近似计算方法讨论了定积分的计算.关键词: 定积分; 计算方法; 二重积分; 近似计算一 引言在数学分析的学习以及科学研究中，到处都会遇到微分、积分的计算问题,微分的计算比较容易，积分的计算难度就要大多了.正因为如此,人们对积分的计算从理论到实践进行了大量的研究,总结了许多种方法.在此，着重对定积分的计算方法和技巧做归类简析.二 正文1根据定义计算定积分定积分的定义]1[:一般地，设函数()f x 在区间[,]a b 上连续，用分点0121i i n a x x x x x x b -=<<<<<<<=将区间[,]a b 任意分成n 个小区间，每个小区间长度为x ∆（b ax n-∆=），在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ= ，作和式：11()()nnn i i i i b aS f x f n ξξ==-=∆=∑∑如果x ∆无限接近于0（亦即n →+∞）时,上述和式n S 无限趋近于常数S ，那么称该常数S 为函数()f x 在区间[,]a b 上的定积分.记为：()baS f x dx =⎰其中()f x 称为被积函数,x 叫做积分变量，[,]a b 为积分区间,b 积分上限，a 积分下限.计算定积分可以通过计算极限ini io x x f ∆∑=→∆1)(lim ξ 来实现.例1]4[ 用定积分的定义求.dx e bax ⎰解 因为xe xf =)(为],[b a 上的连续函数，所以对于任意分割T 和任意点集},{i ξ有i ni i T x f ∆∑=→1)(lim ξ都存在且相等，即dx e bax ⎰存在，所以，把],[b a 平均分成n 等份，因此每个子区间的长度.nab x i -=∆ 取每一子区间的右端点为i ξ,即,i n ab a i -+=ξ于是ni a b a i ef )()(-+=ξ,这样=∆∑=i ni i x f 1)(ξna b a ni ni a b a e nab e-+=-+=-⋅∑(1)(na b a e)(2-++++ nab ena b n a --+))( na b ee nab ee eab na b a na b n nab na b a -⋅-=-⋅-=--+---+)1(]1)[(/),1(--na b e因此dx e bax⎰i ni i n x f ∆=∑=∞→1)(lim ξ∞→=n lim /)1(na b eeab na b a -⋅---+)1(--na b e.)1(a b ab a e e ee -=-=-小结: 用定积分的定义计算定积分,能解决的定积分其被积函数一般是比较简单的情形,主要因为和式x f ni i∆∑=1)(ξ 的极限一般不容易求.2 利用定积分的几何意义计算一般情况下,定积分()baf x dx ⎰的几何意义是介于x 轴、函数()f x 的图形以及直线,x a x b==之间各部分面积的代数和,在x 轴上方的面积取正号,在x 轴下方的面积取负号． 例2 根据定积分的几何意义求下列定积分的值：（1）⎰-x x d 11, （2）⎰--x x R R R d 22, （3）⎰x x d cos 02π, （4）⎰-x x d 11． 解（1）由下图（1）所示,0)(d 1111=+-=⎰-A A x x .- 11 11A A O xyRy2A（2）由上图（2）所示,2d 2222R A x x R RRπ==-⎰-.(3)由上图（3）所示,0)()(d c o s 5353543π20=--++=+-+=⎰A A A A A A A x x .（4）由上图（4）所示,1112122d 611=⋅⋅⋅==⎰-A x x . 3 公式法凡运用不定积分的基本公式和牛顿——菜不尼玆公式计算定积分的方法,称为公式法.公式法适用于解决能用不定积分求出被积函数的原函数的这类函数积分的问题.而用不定积分求原函数时有直接积分、还原积分、分部积分，因此相应地也有定积分的直接积分、还原积分、分部积分法等.牛顿—莱布尼兹公式]1[ 设)(x f 在],[b a 上连续，且)(x F 是)(x f 的一 个原函数,则)()()(a F b F dx x f ba-=⎰． (1)公式(1)是著名的牛顿—莱布尼兹公式.牛顿—莱布尼兹公式把定积分的计算问题归结为求被积函数的原函数在上、下限处函数值之差的问题，从而巧妙地避开了求和式极限的艰难道路,为运用定积分计算普遍存在的总量问题另辟坦途．例如1cos 42]cos [)11sin 2(1212++=+-=+++⎰πarctgx x x dx x x x . O x y1 - 13A 4 A 5 A 2 π π( 3 )1-1- 11 O xy6A 6A (4)4 特殊计算方法 4.1方程式求解在计算过程中,通过解方程（组）的方式求定积分.例3 求xdx e I x sin 20⎰=π.解 xdx e I xsin 20⎰=π=02sin πxe x-xdx e x cos 20⎰π=x xde e cos 202⎰-ππ=⎥⎥⎦⎤⎢⎢⎣⎡+-⎰xdx e xe e x x sin cos 20022πππI e xdx e e x-+=-+=⎰1sin 12202πππ解方程：)1(21122+=⇒-+=ππe I I e I .4.2消项法对某些不便计算的积分,经过一定的变化,将其中某些部分积分相互抵消而得其值.作为一种方法只能尝试着使用. 例4]4[ 求dx x x I ⎰++=1021)1ln(.解 ⎰⎰⎰=-=+=+=404040c o s )4c o s (2ln cos cos sin ln)1ln(ππππdt t t dt t t t dt tgt I tgtx ⎰⎰⎰--+=404040.cos ln )4cos(ln 2ln ππππtdt dt t dt而⎰⎰⎰==--=404044.cos ln cos ln )4cos(ln πππππtdt udu dt t tu.2ln 82ln 40ππ==⎰dt I4.3 利用导数计算定积分例5]5[ ⎰π203.sin xdx x 求解 令,0)(,6)(''',6)('',3)(')()4(23====⇒=x f x f x x f x x f x x f)]2('')0(''[)]2()0([sin )]()([20)4(πππf f f f xdx x f x f ---=-⎰即].120[]80[sin )0(3203πππ---=-⎰xdx x.812sin 2203πππ-=⎰xdx x4.4 利用递推公式例6]5[ 计算xdx e x I xn n sin 20⎰=π.c o s 20x d x e x J x n n ⎰=π解 x d x e x x d x e xn x e x I x n xn xn n c o s s i n s i n2020102⎰⎰--=-πππn n xnJ nI e --=-12)2(π. (2)同理：n n n I nJ J +-=-1. (3)由（2）,（3）得：⎪⎪⎩⎪⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡--⎪⎭⎫ ⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡+-⎪⎭⎫ ⎝⎛=---=112112221221n n n n n n n n nJnI e J nJ nI e I ππππ ,,2,1 =n 其中 2121sin 220+==⎰ππe xdx e I x ,.2121cos 2200-==⎰ππe xdx e J x4.5 利用二重积分计算定积分先将定积分设法化为二重积分,再用二重积分的性质进行计算. 例7]1[ 计算dx xxx I ⎰-=13ln 解,2l n l i m ,0l n l i m 1,0l n 31303=-=--→→-x xx x x x xx x x x ）内连续，且在（ 故 dx x x x ⎰-13ln 有意义，又 ,ln 313dy x xxx y ⎰=-.2l n 11131103131=+===∴⎰⎰⎰⎰⎰dy y dx x dy dy x dx I y y 4.6 利用带参变量的积分计算定积分 例8 计算dx xxx I ⎰-=13ln （即例7） 解 令dx xxx b I b ⎰-=10ln )( )0(≥b ,显然,0)(=b IC b b I bdx x b I b ++=⇒+==⎰)1ln()(11)('10)1(=I 21ln 2ln )1ln()(2ln +=-+=⇒-=∴b b b I C .2ln 213ln)3(=+==∴I I 4.7]3[ 利用留数计算积分这是将实积分转变为复变函数积分,再利用复变函数中留数理论进行计算. 例9 计算.1cos 2dx x x ⎰+∞∞-+解 211)(xx R +=为分母2次,分子0次的有理函数,故上述积分存在.且R(z)在上 半平面只有一个一级极点i ,在实轴上无孤立奇点,又i e z e i z i e z R s iz i iz21)(lim ],)([Re 120-→=+∙-=.221sin 1cos 11222ei e i dx x x i dx x x dx x e ix ππ=∙=+++=+∴-∞+∞-∞+∞-∞+∞-⎰⎰⎰ .)(1cos 2ee R dx x x I e ππ==+=∴⎰+∞∞-5 近似计算法]2[根据定积分的几何意义：dx x f ba⎰)(表示的是以)(x f 为曲边,以x 轴上的区间],[b a 为低的曲边梯形面积的代数和.我们可以用x 轴上的分点b x x x x x n ==,,,,210 ,将曲边梯形的低],[b a 平均分成N 个小区间,每个小区间的长度为,Nab x -=∆过分点作平行于y 轴的线段将整个曲边梯形分成N 个小的曲边梯形,每个小的曲边梯形面积都用已知图形的面积来近似代替.根据已知图形的形状可以分为以下近似计算法：5.1矩形法以第i 个小区间左或右端点对应的函数值x x f x f i i ∆-以为高或,)()1(为低作一个小 矩形,用这个小矩形面积x x f x x f i i ∆∆-)()1(或来近似代替第i 个小曲边梯形的面积（n i ,,2,1 =）， 于是Na b x f dx x f Na b x f x x f dx x f ni i bani i n i i ba-≈--=∆-≈∑⎰∑∑⎰===111)()()1()1()(或上式称为矩形法公式.5.2梯形法以第i 个小区间左右端点i i x x ,1-对应的函数值)(),1(i i x f x f -为上下低,以x ∆为高作一个梯形,其面积为2)]()1([xx f x f i i ∆+-,将其作为第i 个小的曲边梯形面积的近似值),,2,1(n i =，于是 xx f x f x x f x f x x f x f dx x f n n ba∆+++∆++∆+≈-⎰)]()([21)]()([21)]()([21)(12110=)]()()(21)(21[10n n x f x f x f x f n a b ++++- 上式称为梯形公式.5.3辛普森法当分点N=2n 时,每个小区间的长度h=nab 2-,过每个分点作平行于Y 轴的直线,它们与曲线 310222111000,,,).,(,),,(),,()(M M M y x M y x M y x M x f y n n n 过点分别交于点= 可确定一条抛物线,以此抛物线为曲边,以区间[20,x x ]为底边的曲边梯形的面积432210,,);4(3M M M y y y h同理以过点++所确定的抛物线为曲边,以区间],[42x x 为底的曲边梯形面积为n n n M M M y y y h21222432,,)4(3--++过点 确定的抛物线为曲边,以区间],[222n n x x -为低的小曲边梯形面积为)4(321222n n n y y y h++--.于是)](4)(2)[(6)(123122422--+++++++++-≈⎰n n n o bay y y y y y y y Nab dx x f上式成为辛普森公式.例10 分别用矩形法,梯形法,辛普森法计算定积分⎰+1021x dx的近似值.解 将区间[0,1]十等分，个基点上被积函数的值列表如下.(取七位有效数字)i x 0 0.1 0.2 0.3 0.4 0.5 i y10.99009900.96153850.91743120.86206900.8000000i x 0.6 0.7 0.8 0.9 1 i y0.73529410.67114090.60975610.55248620.5① 用矩形法公式去计算（取四位有效数字）8099.0)(1011910102=+++≈+⎰y y y dx x dx（或7600.0)(1011021=+++y y y ） ② 用矩形法公式去计算（取四位有效数字）7850.0)22(1011109210102=++++≈+⎰y y y y y x dx ③ 用辛普森法去计算去计算（取七为有效数字）7853982.0)](2)(4[301184********02=+++++++++≈+⎰y y y y y y y y x dx . 准确值：78539816.04112===⎰πarctg dx x与上述值比较，普森法计算结果有六位有效数字是准确的，更接近于真实值.参考文献:[1]华东师范大学数学系.数学分析（第三版）．高等教育出版社,2001 [2]首都师范大学数学系.数值分析 科学出版社,2000[3]同济大学数学教研组.高等数学（第三版）.高等教育出版社,1988 [4]邓乐斌.数学分析的理论,方法与技巧.华中科技大学出版社. [5]姚允龙.高等数学与数学分析—方法导引.复旦大学出版社,1992。

定积分的计算方法和应用定积分是微积分中的重要概念，用于计算函数图像下的面积以及多种物理量的平均值和总值。

在这篇文章中，我们将讨论定积分的计算方法和应用以及如何将其应用于实际问题中。

一、前提知识在讨论定积分之前，我们需要了解几个微积分的基本概念：1.导数：表示函数在某一点的瞬时变化率，通常表示为f'(x)。

2.不定积分：表示函数f(x)的一个原函数，即求导为f(x)的函数。

3.定积分：表示函数f(x)在区间[a,b]上的积分，通常表示为∫(a,b)f(x)dx。

二、定积分的计算方法让我们看一个例子，计算函数y=x^2在区间[0,1]上的定积分。

我们可以通过以下步骤计算：1.将区间[0,1]分成n个小区间，即将区间[0,1]分成n份，每份的长度为Δx=(b-a)/n，其中a=0，b=1。

2.在每个小区间上选取一个点xi，计算出xi处函数值f(xi)=xi^2。

3.将每个小区间的面积加起来，即计算出所有小长方形的面积之和。

4.当Δx趋近于0时，可以得到定积分的值，即∫(0,1)x^2dx=1/3。

通过以上步骤，我们可以计算出定积分的值。

这种方法称为矩形法，其中每个小长方形的高度为函数在该点的函数值，宽度为每个小区间的长度。

除了矩形法之外，还有其他一些更准确的定积分计算方法，如梯形法、辛普森法等。

这些方法都是通过将区间分成小区间，计算每个小区间上的函数值并将其相加来计算定积分值。

三、定积分的应用定积分有很多实际应用场景，下面我们将介绍一些常见的应用场景。

1.几何应用定积分可以用来计算曲线下的面积，即将曲线所围成的区域看作矩形或梯形的叠加。

这种方法可以用于计算三角形、圆形、椭圆形等几何图形的面积。

另外，定积分也可以用来计算旋转体的体积。

将一个曲线沿着某个轴旋转，那么旋转出来的图形就是一个旋转体。

通过计算曲线下的面积并将其绕轴旋转可以得到旋转体的体积。

2.物理应用定积分还可以用于计算多种物理量的平均值和总值。

钦州学院数学与计算机科学学院数 学 实 验 报 告实验完成日期 2010 年 11 月 5 日 ， 第 10 周 ， 星期五 成绩等级（五级分制） 评阅教师 评阅日期 年 月 日 数学实验报告填写要求：思路清晰，中间结果和最终结果真实；字迹工整，报告完整。

[实验题目及内容]实验题目：（1）通过矩形法、梯形法分别计算定积分⎰++-=bax xx f 32.0)(2的黎曼和；（2）通过10=n ，50=n ，200=n 时黎曼和的值分析两种方法逼近定积分的速度。

内容：黎曼和逼近定积分值的动态过程演示，可利用几何画板制作[问题描述]（用自己组织的相关数学语言重述现实问题；注意对约定的条件作说明）将AB 边n 等分，过这些分点作E B '的垂线，将抛物线32.0)(2++-=x x x f 和以AB 为边形成的图形分割为n 个直角小梯形或小矩形，求这些小梯形或小矩形面积的和，即可求出定积分⎰++-=bax xx f 32.0)(2黎曼和即面积。

当n 充分大时，直角小梯形或小矩形的面积之和可近似代替定积分⎰++-=bax xx f 32.0)(2黎曼和。

因此可通过计算梯形或矩形面积求出定积分⎰++-=bax xx f 32.0)(2的黎曼和。

定积分dx x f ba⎰)(在数值上等于以曲线)(x f y =和三直线0=y 、a x =、b x =所围成的曲边梯形的面积。

解决的办法是分割后再求和：设想将区间],[b a 分为n 个小区间，以每个小区间左端点对应的函数值为高，以小区间的长度为宽，构作n 个梯形或矩形，并以这些小梯形或小矩形的面积的和（即黎曼和）近似代替定积分的面积。

当改变参数n 的大小时，随着n 的逐渐增大（并且每个小区间的长度逐渐缩小），黎曼和的值逐渐趋近定积分的值。

[模型建立或思路分析]（建立合理，可解释的数学模型，通过公式、表格或图形直观明确地描述模型的结构；无法通过建立模型解决的，给出解题的思路及办法。

一.写一个用矩形法求定积分的函数，求sin(x)在（0,1）上的定积分。

#include <stdio.h>#include <math.h>float jifen(float a,float b){int i,l;float n=0.001,s=0; //n表示划分的单位宽度，n越小结果越精确，n是矩形的宽l=(b-a)/n; // l表示有多少个单位宽度for(i=0;i<l;i++)s=n*sin(a+n*i)+s; // sin(a+n*i)是矩形的长printf("用矩形法求得该函数在(%2.0f,%2.0f)上的积分为%f。

\n",a,b,s);}main(){jifen(0,1);}二.写一个用梯形法求定积分的函数，求sin(x)在（0,1）上的定积分。

#include <stdio.h>#include <math.h>float jifen(float a,float b){int i,l;float n=0.001,s=0;l=(b-a)/n;for(i=0;i<l;i++)s=(sin(a+n*i)+sin(a+n*(i+1)))*n/2+s; // (sin(a+n*i)是梯形的上底，sin(a+n*(i+1))是下底printf("用梯形法求得该函数在(%2.0f,%2.0f)上的积分为%f。

\n",a,b,s);}main(){jifen(0,1);}三.（综合）写一个用矩形法和梯形法求定积分的通用函数，分别求sin(x)在（0,1）上、cos(x)在(-1,1)上、exp在（0,2）上的定积分。

说明：jifen的函数定义中，double (*fun)(double)表示fun是指向函数的指针，被指的函数是一个实型函数，有一个实型形参，Fun是指向函数的指针变量。

用jifen(0,1,sin)语句调用jifen 函数时，给jifen函数传递了sin函数的入口地址，这时jifen函数中的fun函数就相当于是sin函数了，(*fun)(a+n*i)相当于sin(a+n*i)。

中矩形法是一种数值积分方法，用于近似计算定积分的值。

该方法将积分区间分成若干小矩形，然后计算这些小矩形的面积之和作为对定积分的近似值。

中矩形法的代数精度为一阶，即在理论上，它可以准确计算一次多项式的定积分。

具体而言，设函数f(x) 在积分区间[a, b] 上连续，并将积分区间等分成n 个小区间，每个小区间的宽度为Δx = (b - a) / n。

则中矩形法的近似积分公式为：
∫[a, b] f(x) dx ≈Δx * (f(x₀+Δx/2) + f(x₁+Δx/2) + ... + f(xₙ₋₁+Δx/2))
其中，x₀, x₁, ..., xₙ₋₁分别表示各小区间的中点。

需要注意的是，尽管中矩形法具有一阶的代数精度，但在实际应用中，它可能无法准确计算复杂函数的定积分，特别是在积分区间上函数变化较大或者存在奇点的情况下。

在这些情况下，更高阶的数值积分方法，如梯形法则或辛普森法则，可能提供更准确的近似值。