2020届江苏省姜堰中学2017级高三下学期3月调研考试数学试卷(含附加题)及答案

江苏省2020届高三尖子生班3月调研考试数学试题含附加题------------------------------------------作者xxxx------------------------------------------日期xxxx2 / 24数学试卷第 2 页 共 24 页20２0届高三尖子生班3月调研考试数学试题数学(一) 20２０．3一、填空题:本大题共14小题,每小题5分，计70分．请把答案写在答．题卡相应位置上．．．．．．． １．已知集合0(1)2,0,12x x Ax yBx x Z x xx ,则A B = .2.在“一带一路”（英文：Ｔh ｅ Belt and Roa ｄ,缩写B&R ）知识问答竞赛中,“江苏”代表队的七名选手的比赛成绩的茎叶统计图如图所示,去掉一个最高分和一个最低分，所剩数据的方差为 ．３．复数ｚ满足13i z ,i 为虚数单位,错误!为复数z 的共轭复数,则复数42zz 的模为 .4．随机掷出5个标准的骰子，得到５个点数之和是1１的概率为 ．5．执行如图所示的算法流程图，则输出的a 的值是 .注意事项考生在答题前请认真阅读本注意事项及各题答题要求.1. 本试卷包含填空题（第1题--第14题）、解答题（第15题--第20题）.本卷满分160 分考试时间为120分钟.2. 答题前，请务必将自己的姓名、准考证号用0.5毫米黑色签字笔填写在规定位置.3. 请在答题卡上按顺序在对应的答题区域内作答，在其他位置作答一律无效.作答必须用0.5毫米黑色签字笔.注意字体工整，笔记清楚.4. 如需作图，需用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗.6．曲线2233x y与228y x x的四个交点所在圆的方程是．7．已知π0,2，π1cos33，则πcos26的值是 .8. 在矩形ABCD中，3,4AB BC，点E在边BＣ上，点F在边CD 上。

若2EF，则AE AF的最小值是．9．设椭圆22221(0x ya ba b)的左焦点为F,过椭圆上一点A作椭圆的切线交y 轴于点Q 若,46QFO QFA，则此椭圆的离心率为 .10.在正方体盒子里放入四个半径为1的球,恰好使得两个球在下方,另外两个在上方,每个球都和其他球相切,且它们都和正方体的三个面相切。

高三数学测试数学I注意事项考生在答题前请认真阅读本注意事项及答题要求1．本试卷共4页，包含填空题（第1题～第14题）、解+析题（第15题～第20题）．本卷满分为160分，考试时间为120分钟．考试结束后，请将答题卡交回．2．答题前，请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．作答试题，必须用0.5毫米黑色墨水的签字笔在答题卡上指定位置作答，在其它位置作答一律无效．4．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、填空题（本大题共14小题，每小题5分，计70分. 不需写出解答过程，请把答案写在答题纸的指定位置上）1、全集12{}345U＝，，，，，集合134{}}35{A B＝，，，＝，，则UA B⋂（）ð= ．2、已知i是虚数单位，若12i a i a R+∈（﹣)(）＝，，则a＝．3、我国古代数学算经十书之一的《九章算术》一哀分问题：今有北乡八千一百人，西乡九千人，南乡五千四百人，凡三乡，发役五百，意思是用分层抽样的方法从这三个乡中抽出500人服役，则北乡比南乡多抽人．4、已知一组数据17,18,19,20,21，则该组数据的方差是．5、双曲线1222=-yx的渐近线方程为．6、已知)1sin()(-=xxf，若{}7,5,3,1∈p，则0)(≤pf的概率为．7、已知棱长均为2的正四棱锥与底面边长为2的正四棱柱的体积相等，则正四棱柱的高为．8、已知函数22353log(1)3x xf xx x-⎧-<⎨-+≥⎩（）＝，若6)(-=mf，则)61(-mf＝．9、已知函数()2cos([0,])f x x xπ=∈的图象与函数g（x）=3tanx的图象交于点A,B，点O为坐标原点，则OAB∆的面积为．10、已知正方形ABCD的边长为4，M是AD的中点，动点N在正方形ABCD的内部或其边界移动，并且满足0MN AN⋅=u u u u r u u u r，则NB NC⋅u u u r u u u r的最小值是．11、在ABC∆中，若sin cosB B+=则sin2tan tanAB C+的最大值为．BC12、在平面直角坐标系xOy 中，A 和B 是圆()22:11C x y -+=上两点，且2AB =，点P 的坐标为)1,2(，则2PA PB -u u u r u u u r的最小值为 ．13、已知2,0,()9x y xy x y >+=，则y x +2的最小值为 ．14、已知集合{}{}**∈-==∈-==N k k x x B N k k x x A ,88,,12，从集合A 中取出m 个不同元素，其和记为S ；从集合B 中取出n 个不同元素，其和记为T ．若967≤+T S ，则n m 2+的最大值为 ． 二、解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤. 15、（本小题满分14分） 在△ABC 中，角ABC 的对边分别为a,b,c ，且222(cos cos )a b a B b A -=+. （1）求角A 的大小；（2）若D 是BC 边上一点，AD=10，AC=14，DC=6，求AB 的长. 16、（本小题满分14分）如图，在四棱锥S ABCD -中，已知SA SB =，四边形ABCD 是平行四边形，且平面SAB ⊥平面ABCD ，点M ，N 分别是SC ，AB 的中点. （1）求证：//MN 平面SAD ； （2）求证：SN AC ⊥.xyOF ABMN（第18题）17、（本小题满分14分）如图，某市建有贯穿东西和南北的两条垂直公路l 1，l 2，在它们交叉路口点O 处的东北方向建有一个荷花池，荷花池的外围是一条环形公路，荷花池中的固定观景台P 位于两条垂直公路的角平分线l 上，l 与环形公路的交点记作M.游客游览荷花池时，需沿公路OM 先到达环形公路M 处。

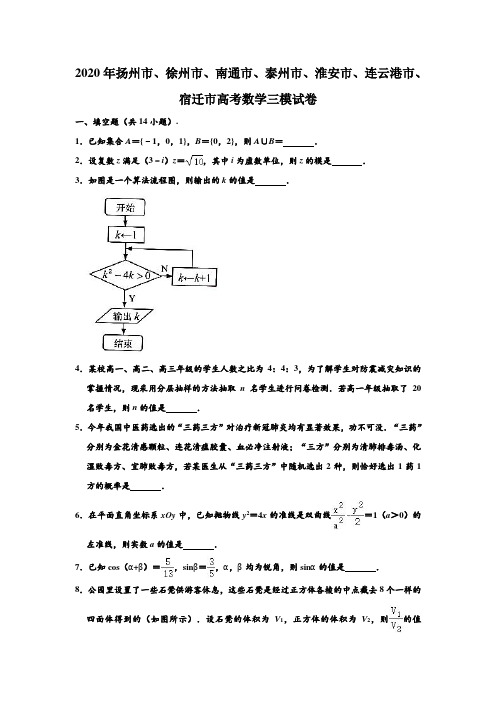
2020年扬州市、徐州市、南通市、泰州市、淮安市、连云港市、宿迁市高考数学三模试卷一、填空题（共14小题）.1．已知集合A＝{﹣1，0，1}，B＝{0，2}，则A∪B＝．2．设复数z满足（3﹣i）z＝，其中i为虚数单位，则z的模是．3．如图是一个算法流程图，则输出的k的值是．4．某校高一、高二、高三年级的学生人数之比为4：4：3，为了解学生对防震减灾知识的掌握情况，现采用分层抽样的方法抽取n名学生进行问卷检测．若高一年级抽取了20名学生，则n的值是．5．今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果，功不可没．“三药”分别为金花清感颗粒、连花清瘟胶囊、血必净注射液；“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方，若某医生从“三药三方”中随机选出2种，则恰好选出1药1方的概率是．6．在平面直角坐标系xOy中，已知抛物线y2＝4x的准线是双曲线＝1（a＞0）的左准线，则实数a的值是．7．已知cos（α+β）＝，sinβ＝，α，β均为锐角，则sinα的值是．8．公园里设置了一些石凳供游客休息，这些石凳是经过正方体各棱的中点截去8个一样的四面体得到的（如图所示）．设石凳的体积为V1，正方体的体积为V2，则的值是．9．已知x＞1，y＞1，xy＝10，则的最小值是．10．已知等比数列{a n}的前n项和为S n，若4S2，S4，﹣2S3成等差数列，且a2+a3＝2，则a6的值是．11．海伦（Heron，约公元1世纪）是古希腊亚历山大时期的数学家，以他的名字命名的“海伦公式”是几何学中的著名公式，它给出了利用三角形的三边长a，b，c计算其面积的公式S△ABC＝，其中p＝，若a＝5，b＝6，c＝7，则借助“海伦公式”可求得△ABC的内切圆的半径r的值是．12．如图，△ABC为等边三角形，分别延长BA，CB，AC到点D，E，F，使得AD＝BE ＝CF．若，且DE＝，则的值是．13．已知函数f（x）＝，若函数g（x）＝f（﹣x）+f（x）有且仅有四个不同的零点，则实数k的取值范围是．14．在平面直角坐标系xOy中，过点P（2，﹣6）作直线交圆O：x2+y2＝16于A，B两点，C（x0，y0）为弦AB的中点，则的取值范围是．二、解答题（本大题共6小题，共计90分．请在答题纸指定区域内作答，解答应写出文字说明，证明过程或演算步骤．）15．△ABC中，角A，B，C所对的边分别为a，b，c．若．（1）求cos C的值；（2）若A＝C，求sin B的值．16．如图，在直三棱柱ABC﹣A1B1C1中，AC⏊BC，D，E分别是A1B1，BC的中点．求证：（1）平面ACD⊥平面BCC1B1；（2）B1E∥平面ACD．17．某单位科技活动纪念章的结构如图所示，O是半径分别为1cm，2cm的两个同心圆的圆心，等腰△ABC的顶点A在外圆上，底边BC的两个端点都在内圆上，点O，A在直线BC的同侧．若线段BC与劣弧所围成的弓形面积为S1，△OAB与△OAC的面积之和为S2，设∠BOC＝2θ．（1）当θ＝时，求S2﹣S1的值；（2）经研究发现当S2﹣S1的值最大时，纪念章最美观，求当纪念章最美观时，cosθ的值．（求导参考公式：（sin2x）'＝2cos2x，（cos2x）'＝﹣2sin2x）18．（16分）如图，在平面直角坐标系xOy中，已知椭圆＝1（a＞b＞0）的左、右焦点分别为F1，F2，过点F2的直线交椭圆于M，N两点．已知椭圆的短轴长为2，离心率为．（1）求椭圆的标准方程；（2）当直线MN的斜率为时，求F1M+F1N的值；（3）若以MN为直径的圆与x轴相交的右交点为P（t，0），求实数t的取值范围．19．（16分）已知{a n}是各项均为正数的无穷数列，数列{b n}满足b n＝a n•a n+k（n∈N*），其中常数k为正整数．（1）设数列{a n}前n项的积，当k＝2时，求数列{b n}的通项公式；（2）若{a n}是首项为1，公差d为整数的等差数列，且b2﹣b1＝4，求数列的前2020项的和；（3）若{b n}是等比数列，且对任意的n∈N*，a n•a n+2k＝a n+k2，其中k≥2，试问：{a n}是等比数列吗？请证明你的结论．20．（16分）已知函数f（x）＝，g（x）＝，其中e是自然对数的底数．（1）若函数f（x）的极大值为，求实数a的值；（2）当a＝e时，若曲线y＝f（x）与y＝g（x）在x＝x0处的切线互相垂直，求x0的值；（3）设函数h（x）＝g（x）﹣f（x），若h（x）＞0对任意的x∈（0，1）恒成立，求实数a的取值范围．【选做题】本题包括21，22，23三小题，请选定其中两题作答，每小题10分,共计20分，解答时应写出文字说明，证明过程或演算步骤．[选修4-2：矩阵与变换]21．已知m∈R，＝是矩阵M＝的一个特征向量，求M的逆矩阵M﹣1．[选修4-4：坐标系与参数方程]22．在极坐标系中，圆C的方程为ρ＝2r sinθ（r＞0）．以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系，直线l的参数方程为（t为参数）．若直线l与圆C恒有公共点，求r的取值范围．[选修4-5：不等式选讲]23．已知x＞1，y＞1，且x+y＝4，求证：≥8．【必做题】第24题、第25题，每题10分，共计20分，解答时应写出文字说明，证明过程或演算步骤．24．某“芝麻开门”娱乐活动中，共有5扇门，游戏者根据规则开门，并根据打开门的数量获取相应奖励．已知开每扇门相互独立，且规则相同，开每扇门的规则是：从给定的6把钥匙（其中有且只有1把钥匙能打开门）中，随机地逐把抽取钥匙进行试开，钥匙使用后不放回．若门被打开，则转为开下一扇门；若连续4次未能打开，则放弃这扇门，转为开下一扇门；直至5扇门都进行了试开，活动结束．（1）设随机变量X为试开第一扇门所用的钥匙数，求X的分布列及数学期望E（X）；（2）求恰好成功打开4扇门的概率．25．如图，在平面直角坐标系xOy中，已知抛物线y2＝2px（p＞0）的焦点为F，准线与x 轴的交点为E．过点F的直线与抛物线相交于A，B两点，EA，EB分别与y轴相交于M，N两点，当AB⊥x轴时，EA＝2．（1）求抛物线的方程；（2）设△EAB的面积为S1，△EMN面积为S2，求的取值范围．参考答案一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请将答案填写在答题卡相应的位置上．）1．已知集合A＝{﹣1，0，1}，B＝{0，2}，则A∪B＝{﹣1，0，1，2}．【分析】进行并集的运算即可．解：∵A＝{﹣1，0，1}，B＝{0，2}，∴A∪B＝{﹣1，0，1，2}．故答案为：{﹣1，0，1，2}．2．设复数z满足（3﹣i）z＝，其中i为虚数单位，则z的模是1．【分析】把已知等式变形，再由商的模等于模的商求解．解：由（3﹣i）z＝，得z＝，∴|z|＝||＝．故答案为：1．3．如图是一个算法流程图，则输出的k的值是5．【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量k的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．解：模拟程序的运行，可得k＝1不满足条件k2﹣4k＞0，执行循环体，k＝2不满足条件k2﹣4k＞0，执行循环体，k＝3不满足条件k2﹣4k＞0，执行循环体，k＝4不满足条件k2﹣4k＞0，执行循环体，k＝5此时，满足条件k2﹣4k＞0，退出循环，输出k的值为5．故答案为：5．4．某校高一、高二、高三年级的学生人数之比为4：4：3，为了解学生对防震减灾知识的掌握情况，现采用分层抽样的方法抽取n名学生进行问卷检测．若高一年级抽取了20名学生，则n的值是55．【分析】先求出高一年级学生占的比例，再根据比例即可求解结论．解：高一年级学生占的比例为＝，故应满足：＝⇒n＝55人，故答案为：55．5．今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果，功不可没．“三药”分别为金花清感颗粒、连花清瘟胶囊、血必净注射液；“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方，若某医生从“三药三方”中随机选出2种，则恰好选出1药1方的概率是．【分析】某医生从“三药三方”中随机选出2种，基本事件总数n＝＝15，恰好选出1药1方包含的基本事件个数m＝＝9．由此能求出恰好选出1药1方的概率．解：“三药三方”对治疗新冠肺炎均有显著效果，功不可没．“三药”分别为金花清感颗粒、连花清瘟胶囊、血必净注射液，“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方，若某医生从“三药三方”中随机选出2种，基本事件总数n＝＝15，恰好选出1药1方包含的基本事件个数m＝＝9．∴恰好选出1药1方的概率是p＝＝＝．故答案为：．6．在平面直角坐标系xOy中，已知抛物线y2＝4x的准线是双曲线＝1（a＞0）的左准线，则实数a的值是．【分析】求出抛物线的准线方程，求出双曲线的左准线方程，得到关系式，求解即可．解：抛物线y2＝4x的准线是双曲线＝1（a＞0）的左准线，可得：﹣1＝﹣＝﹣，解得a＝．故答案为：．7．已知cos（α+β）＝，sinβ＝，α，β均为锐角，则sinα的值是．【分析】由α，β的范围得出α+β的范围，然后利用同角三角函数间的基本关系，由cos （α+β）和sinβ的值，求出sin（α+β）和cosβ的值，然后由α＝（α+β）﹣β，把所求的式子利用两角差的正弦函数公式化简后，将各自的值代入即可求出值．解：解：由cos（α+β）＝，sinβ＝，根据α，β∈（0，），得到α+β∈（0，π），所以sin（α+β）＝＝，cosβ＝＝，则sinα＝sin[（α+β）﹣β]＝sin（α+β）cosβ﹣cos（α+β）sinβ＝×﹣×＝．故答案为：．8．公园里设置了一些石凳供游客休息，这些石凳是经过正方体各棱的中点截去8个一样的四面体得到的（如图所示）．设石凳的体积为V1，正方体的体积为V2，则的值是．【分析】设正方体的棱长为2a，求出正方体的体积，再由正方体的体积减去8个三棱锥的体积得石凳的体积，则答案可求．解：设正方体的棱长为2a，则正方体的体积．由题意可得，石凳的体积为V1＝8a3﹣＝．∴＝．故答案为：．9．已知x＞1，y＞1，xy＝10，则的最小值是9．【分析】利用“乘1法”与基本不等式的性质即可得出．解：因为x＞1，y＞1，xy＝10，所以lgx+lgy＝1，则＝（）（lgx+lgy）＝5+＝9，当且仅当时即lgy＝2lgx且xy＝10即x＝，y＝时取等号，故答案为：9．10．已知等比数列{a n}的前n项和为S n，若4S2，S4，﹣2S3成等差数列，且a2+a3＝2，则a6的值是﹣32．【分析】等比数列{a n}的公比设为q，运用等差数列的中项性质和等比数列的通项公式，解方程可得首项和公比，进而得到所求值．解：等比数列{a n}的公比设为q，前n项和为S n，若4S2，S4，﹣2S3成等差数列，则2S4＝4S2﹣2S3，可得2（a1+a1q+a1q2+a1q3）＝4（a1+a1q）﹣2（a1+a1q+a1q2），化为2+q＝0，可得q＝﹣2，由a2+a3＝2，可得﹣2a1+4a1＝2，解得a1＝1，则a6＝1•（﹣2）5＝﹣32，故答案为：﹣32．11．海伦（Heron，约公元1世纪）是古希腊亚历山大时期的数学家，以他的名字命名的“海伦公式”是几何学中的著名公式，它给出了利用三角形的三边长a，b，c计算其面积的公式S△ABC＝，其中p＝，若a＝5，b＝6，c＝7，则借助“海伦公式”可求得△ABC的内切圆的半径r的值是．【分析】利用S△ABC＝＝pr，代入即可得出．解：∵a＝5，b＝6，c＝7，∴p＝＝＝9．则S△ABC＝＝r×（5+6+7），可得：r＝．故答案为：．12．如图，△ABC为等边三角形，分别延长BA，CB，AC到点D，E，F，使得AD＝BE ＝CF．若，且DE＝，则的值是．【分析】设AD＝BE＝CF＝x，由于，所以BA＝2AD＝2x＝AC＝BC，BD＝3x．在△BDE中，由余弦定理知，，代入数据可解得x＝1，从而有AF＝3，CE＝3，然后结合平面向量数量积的运算即可得解．解：设AD＝BE＝CF＝x，∵，∴BA＝2AD＝2x＝AC＝BC，∴BD＝BA+AD＝3x，在△BDE中，由余弦定理知，，即，解得x＝1．∴AF＝3，CE＝3，∴＝．故答案为：．13．已知函数f（x）＝，若函数g（x）＝f（﹣x）+f（x）有且仅有四个不同的零点，则实数k的取值范围是（27，+∞）．【分析】表示出函数g（x），分k＝0，k＜0及k＝0讨论，易知当k＝0及k＜0时均不合题意，而观察解析式可知，问题可化为有且仅有两个不同的零点，故利用导数研究函数g（x）在（0，+∞）上的最小值小于0即可．解：依题意，，当k＝0时，原函数有且只有一个零点，不合题意，故k≠0；观察解析式，易知函数g（x）为偶函数，则函数g（x）有且仅有四个不同的零点，可转化为有且仅有两个不同的零点，当k＜0时，函数g（x）在（0，+∞）上递增，最多一个零点，不合题意；当k＞0时，，令g′（x）＞0，解得，令g′（x）＜0，解得，故函数g（x）在上递减，在上递增，要使g（x）在（0，+∞）上有且仅有两个不同的零点，则，解得k＞27．故答案为：（27，+∞）．14．在平面直角坐标系xOy中，过点P（2，﹣6）作直线交圆O：x2+y2＝16于A，B两点，C（x0，y0）为弦AB的中点，则的取值范围是[，）．【分析】作出图象，根据条件可求得点C的运动轨迹为x2+y2﹣2x+6y＝0，的取值范围可转化为求点C与点Q（﹣1，3）的距离范围，数形结合即可解：如图所示，由圆的性质知：PC⊥OC，∴•＝0，又∵＝（x0﹣2，y0+6），＝（x0，y0），则•＝x0（x0﹣2）+y0（y0+6）＝x02+y02﹣2x0+6y0＝0∴点C的轨迹方程为圆：x2+y2﹣2x+6y＝0即（x﹣1）2+（y+3）2＝10，圆心（1，﹣3），半径r＝则的取值范围可转化为求点C与点Q（﹣1，3）的距离范围如图所示，因为点C在圆O内，故只需求出OQ和QM或QN的长度即可，易得OQ＝＝，联立，整理得2x﹣6y﹣16＝0即直线MN方程为x﹣3y﹣8＝0，再联立，解得，，即M（，），N（，），故QM＝＝QN＝＝，因为C取不到M或N点，故的取值范围是[，）．故答案为：[，）．二、解答题（本大题共6小题，共计90分．请在答题纸指定区域内作答，解答应写出文字说明，证明过程或演算步骤．）15．△ABC中，角A，B，C所对的边分别为a，b，c．若．（1）求cos C的值；（2）若A＝C，求sin B的值．【分析】（1）利用正弦定理转化条件，利用余弦定理求得cos C的值；（2）利用三角函数的内角和定理与三角恒等变换，即可求出sin B的值．解：（1）△ABC中，，由正弦定理得＝，整理得5（a2+b2﹣c2）＝8ab，由余弦定理得cos C＝＝＝；（2）由（1）知cos C＝，C是△ABC的内角，所以sin C＝＝；又A＝C，所以sin B＝sin（π﹣A﹣C）＝sin（A+C）＝sin2C＝2sin C cos C＝2××＝．16．如图，在直三棱柱ABC﹣A1B1C1中，AC⏊BC，D，E分别是A1B1，BC的中点．求证：（1）平面ACD⊥平面BCC1B1；（2）B1E∥平面ACD．【分析】（1）推导出AC⊥CC1，AC⊥平面BCC1B1，由此能证明平面ACD⊥平面BCC1B1．（2）取AC中点F，连结EF，DF，推导出四边形B1DFE为平行四边形，从而B1E∥DF，由此能证明B1E∥平面ACD．【解答】证明：（1）直三棱柱ABC﹣A1B1C1中，CC1⊥底面ABC，又AC⊂底面ABC，∴AC⊥CC1，∵AC⊥BC1，CC1∩BC＝C，∴AC⊥平面BCC1B1，∵AC⊂平面ACD，∴平面ACD⊥平面BCC1B1．（2）取AC中点F，连结EF，DF，∵E，F分别为BC，AC中点，∴EF∥AB，EF＝，直三棱柱ABC﹣A1B1C1中，AB A1B1，∵D为A1B1中点，∴B1D∥AB，B1D＝，∴EF B1D，∴四边形B1DFE为平行四边形，∴B1E∥DF，∵DF⊂平面ACD，B1E⊄平面ACD，∴B1E∥平面ACD．17．某单位科技活动纪念章的结构如图所示，O是半径分别为1cm，2cm的两个同心圆的圆心，等腰△ABC的顶点A在外圆上，底边BC的两个端点都在内圆上，点O，A在直线BC的同侧．若线段BC与劣弧所围成的弓形面积为S1，△OAB与△OAC的面积之和为S2，设∠BOC＝2θ．（1）当θ＝时，求S2﹣S1的值；（2）经研究发现当S2﹣S1的值最大时，纪念章最美观，求当纪念章最美观时，cosθ的值．（求导参考公式：（sin2x）'＝2cos2x，（cos2x）'＝﹣2sin2x）【分析】（1）结合弓形面积公式及三角形的面积公式分别求出S2，S1，然后结合三角函数的性质即可求解；（2）结合（1）的面积表示，结合导数与单调性的关系可求．解：（1）由题意可知，∠BOC＝2θ∈（0，π），故，S1＝＝θ﹣sinθcosθ＝，S2＝﹣sin2θ＝﹣sin2θ＝2sinθ，当时，S1＝，S2＝，故S2﹣S1＝（cm2），（2）S2﹣S1＝2sinθ+sin2θ﹣θ，，令f（θ）＝2sinθ+sin2θ﹣θ，，则f′（θ）＝2cosθ+cos2θ﹣1＝2cos2θ+2cosθ﹣2，令f′（θ）＝0可得，cosθ＝（舍负），记cosθ0＝，，当θ∈（0，θ0）时，f′（θ）＞0，函数单调递增，当时，f′（θ）＜0，函数单调递减，故当θ＝θ0时，即cosθ＝时，f（θ）取得最大值，即S2﹣S1取得最大值．18．（16分）如图，在平面直角坐标系xOy中，已知椭圆＝1（a＞b＞0）的左、右焦点分别为F1，F2，过点F2的直线交椭圆于M，N两点．已知椭圆的短轴长为2，离心率为．（1）求椭圆的标准方程；（2）当直线MN的斜率为时，求F1M+F1N的值；（3）若以MN为直径的圆与x轴相交的右交点为P（t，0），求实数t的取值范围．【分析】（1）设焦距为2c，运用离心率公式，可得a，b，c的方程，解方程可得a，b，进而得到椭圆方程；（2）由（1）可得c＝2，即F1（﹣2，0），F2（2，0），联立直线方程和椭圆方程，求得M，N，即可得到所求和；（3）方法一、讨论直线MN的斜率不存在，求得|MN|，可得t的值；MN的斜率存在时，设MN：y＝k（x﹣2），M（x1，y1），N（x2，y2），联立椭圆方程，运用韦达定理和中点坐标公式，弦长公式，结合圆的方程和换元，运用函数的单调性可得所求范围；方法二、运用直径所对的圆周角为直角，结合向量的数量积的性质和坐标表示，化简整理，可得t的不等式组，解得t的范围．解：（1）设焦距为2c，则2b＝2，b2＝a2﹣c2，e＝＝，解得a＝，b＝，则椭圆的方程为+＝1；（2）由（1）可得c＝2，即F1（﹣2，0），F2（2，0），由可得或，即M（，），N（，﹣）或N（，），M（，﹣），因此|F1M|+|F1N|＝+＝；（3）方法一、①MN的斜率不存在时，MN：x＝2，|MN|＝，以MN为直径的圆的方程为（x﹣2）2+y2＝，其与x轴相交的右交点为P（2+，0），即t＝2+；②MN的斜率存在时，设MN：y＝k（x﹣2），M（x1，y1），N（x2，y2），由，可得（1+3k2）x2﹣12k2x+12k2﹣6＝0，△＝（12k2）2﹣4（1+3k2）（12k2﹣6）＝24（k2+1）＞0恒成立，x1+x2＝，x1x2＝，|x1﹣x2|＝＝＝，y1+y2＝k（x1+x2）﹣4k＝k•﹣4k＝﹣，则MN的中点为（，﹣），|MN|＝•|x1﹣x2|＝•＝，故以MN为直径的圆的方程为（x﹣）2+（y+）2＝，令y＝0，可得x＝，由题意可得t＝，可令1+3k2＝m（m≥1），则k2＝，t＝2﹣+，可令x＝，x∈（0，2]，可得t＝2﹣x+，可令f（x）＝2﹣x+，x∈（0，2），由于（x+）2＜x2+x+，则f′（x）＝＜0，故f（x）在（0，2）递减，f（0）＝2+，f（2）＝，因此f（x）∈[，2+），综上可得t∈[，2+]．方法二、x1x2＝，则y1y2＝k2（x1﹣2）（x2﹣2）＝k2[x1x2﹣2（x1+x2）+4]＝k2[﹣2•+4]＝﹣，P在以MN为直径的圆上，则•＝0，（x1﹣t）（x2﹣t）+y1y2＝0，x1x2﹣t（x1+x2）+t2+y1y2＝0，即﹣+t2﹣＝0，化为（3t2﹣12t+10）k2＝6﹣t2，由于P为右交点，故t＞2，因此，解得t∈[，2+]．19．（16分）已知{a n}是各项均为正数的无穷数列，数列{b n}满足b n＝a n•a n+k（n∈N*），其中常数k为正整数．（1）设数列{a n}前n项的积，当k＝2时，求数列{b n}的通项公式；（2）若{a n}是首项为1，公差d为整数的等差数列，且b2﹣b1＝4，求数列的前2020项的和；（3）若{b n}是等比数列，且对任意的n∈N*，a n•a n+2k＝a n+k2，其中k≥2，试问：{a n}是等比数列吗？请证明你的结论．【分析】（1）直接利用关系式的变换的应用求出数列通项公式．（2）首先求出数列的通项公式，进一步利用裂项相消法在数列求和中的应用求出结果．（3）利用等比数列的的定义的应用求出结果．解：（1）因为，所以（n≥2），两式相除得：＝2n﹣1（n≥2），当n＝1时，，符号上式，∴（n∈N*），当k＝2时，b n＝a n•a n+2＝2n﹣1•2n+1＝4n；（2）由于b n＝a n a n+1，且a1＝1，所以b1＝a1a k+1＝a k+1，b2＝a2a k+2＝（d+1）（a k+1+d）．所以＝4，由于d和k都为正整数，所以d≥1，所以a k+1≥a2＝1+d≥2，所以d2+d（a k+1+1）＝4≥d2+3d．解得d≤1，所以d＝1，即a n＝n．所以d2+d（a k+1+1）＝4＝a k+1+2，即a k+1＝2，解得k＝1．所以b n＝a n+1a n＝n（n+1），所以．则：，所以．（3）{b n}是等比数列，公比为，且对任意的n∈N*，所以＝q2k．a n•a n+2k＝a n+k2，所以，所以，所以＝，则，所以．故数列{a n}是等比数列．20．（16分）已知函数f（x）＝，g（x）＝，其中e是自然对数的底数．（1）若函数f（x）的极大值为，求实数a的值；（2）当a＝e时，若曲线y＝f（x）与y＝g（x）在x＝x0处的切线互相垂直，求x0的值；（3）设函数h（x）＝g（x）﹣f（x），若h（x）＞0对任意的x∈（0，1）恒成立，求实数a的取值范围．【分析】（1）由题意可知a＞0，先对f（x）求导，分析单调性，得到极大值，让其等于，即可解得a的值．（2）分别求出f（x），g（x）在x＝x0处切线的斜率，让它们乘积等于1，即可解得x0的值．（3）问题可以转化为，对任意x∈（0，1）恒成立，设H（x）＝，由（1）可知，H（x）在（0，1）上单调递增，且当x∈（1，+∞）时，H（x）＞0，当x∈（0，1）时，H（x）＜0，可得ae x＞x，也就是ae x＞x对任意x∈（0，1）恒成立，即，设G（x）＝（x∈（0，1）），只要G（x）max≤a，即可得出答案．解：（1）因为f（x）＝，则f′（x）＝＝，因为g（x）＝，所以a＞0，则当x∈（0，e）时，f′（x）＞0，f（x）单调递增，当x∈（e，+∞）时，f′（x）＜0，f（x）单调递减，所以当x＝e时，f（x）的极大值f（e）＝＝，解得a＝1．（2）当a＝e时，f（x）＝，g（x）＝，则f′（x）＝，g′（x）＝，由题意可知，f′（x0）g′（x0）＝•＝﹣1，整理得x0e+elnx0＝e，设φ（x）＝xe x+elnx，则φ′（x）＝（x+1）e x+＞0，所以φ（x）单调递增，因为φ（1）＝e，所以x0＝1．（3）由题意可知，＞0，对任意x∈（0，1）恒成立，整理得，对任意x∈（0，1）恒成立，设H（x）＝，由（1）可知，H（x）在（0，1）上单调递增，且当x∈（1，+∞）时，H（x）＞0，当x∈（0，1）时，H（x）＜0，若ae x≥1＞x，则H（ae x）≥0＞H（x），若0＜ae x＜1，则H（ae x）＞H（x），且H（x）在（0，1）上单调递增，所以ae x＞x，综上可知，ae x＞x对任意x∈（0，1）恒成立，即，设G（x）＝（x∈（0，1）），则G′（x）＝＞0，所以G（x）单调递增，所以G（x）＜G（1）＝≤a，即a的取值范围为[，+∞）．【选做题】本题包括21，22，23三小题，请选定其中两题作答，每小题10分,共计20分，解答时应写出文字说明，证明过程或演算步骤．[选修4-2：矩阵与变换]21．已知m∈R，＝是矩阵M＝的一个特征向量，求M的逆矩阵M﹣1．【分析】由＝是属于特征值n的一个特征向量，得M＝n，然后求出m，得到矩阵M，再设矩阵的逆矩阵M﹣1＝，由MM﹣1＝，求出M的逆矩阵M﹣1．解：由＝是属于特征值n的一个特征向量，得M＝n，∵M＝＝，＝n＝，∴1+m＝3＝n，解得m＝2，∴矩阵M＝，设矩阵的逆矩阵M﹣1＝，则MM﹣1＝＝＝，∴，解得a＝﹣，b＝，c＝，d＝﹣，解得M﹣1＝．[选修4-4：坐标系与参数方程]22．在极坐标系中，圆C的方程为ρ＝2r sinθ（r＞0）．以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系，直线l的参数方程为（t为参数）．若直线l与圆C恒有公共点，求r的取值范围．【分析】求出圆的直角坐标方程，把直线的参数方程化为普通方程，利用点到直线的距离与半径列出不等式求解即可．解：由ρ＝2r sinθ得ρ2＝2rρsinθ，∴圆C的方程为x2+y2﹣2ry＝0，把参数方程为（t为参数），消去参数t，可得：普通方程：x﹣y﹣2＝0，直线与圆有公共点，可得：d＝≤r，解得r≥2．∴实数r的取值范围为[2，+∞）．[选修4-5：不等式选讲]23．已知x＞1，y＞1，且x+y＝4，求证：≥8．【分析】设x﹣1＝m，y﹣1＝n，则m＞0，n＞0，且m+n＝2，再利用基本不等式即可得证．【解答】证明：设x﹣1＝m，y﹣1＝n，又x＞1，y＞1，则m＞0，n＞0，且m+n＝x+y ﹣2＝2，∴＝，当且仅当m＝n＝1，即x＝y＝2时，等号成立，故原命题得证．【必做题】第24题、第25题，每题10分，共计20分，解答时应写出文字说明，证明过程或演算步骤．24．某“芝麻开门”娱乐活动中，共有5扇门，游戏者根据规则开门，并根据打开门的数量获取相应奖励．已知开每扇门相互独立，且规则相同，开每扇门的规则是：从给定的6把钥匙（其中有且只有1把钥匙能打开门）中，随机地逐把抽取钥匙进行试开，钥匙使用后不放回．若门被打开，则转为开下一扇门；若连续4次未能打开，则放弃这扇门，转为开下一扇门；直至5扇门都进行了试开，活动结束．（1）设随机变量X为试开第一扇门所用的钥匙数，求X的分布列及数学期望E（X）；（2）求恰好成功打开4扇门的概率．【分析】（1）根据互斥事件概率公式计算X的可能取值对应的概率，得出分布列和数学期望；（2）根据二项分布的概率公式计算概率．解：（1）X的可能取值为1，2，3，4，P（X＝1）＝，P（X＝2）＝＝，P（X＝3）＝＝，P（X＝4）＝＝，∴X的分布列是：X1234PE（X）＝1×+2×+3×+4×＝3．（2）每扇门被打开的概率为＝，设被打开的门的数量为ξ，则ξ～B（5，），∴恰好成功打开4扇门的概率为：P（ξ＝4）＝•（）4•＝．25．如图，在平面直角坐标系xOy中，已知抛物线y2＝2px（p＞0）的焦点为F，准线与x 轴的交点为E．过点F的直线与抛物线相交于A，B两点，EA，EB分别与y轴相交于M，N两点，当AB⊥x轴时，EA＝2．（1）求抛物线的方程；（2）设△EAB的面积为S1，△EMN面积为S2，求的取值范围．【分析】（1）求得抛物线的焦点坐标，以及E的坐标，运用两点间的距离公式，解得p，进而得到抛物线的方程；（2）设AB：x＝my+，A（x1，y1），B（x2，y2），联立抛物线的方程，运用韦达定理，以及直线方程，求得M，N的坐标，化简整理，运用三角形的面积公式，化简整理，结合韦达定理，即可得到所求范围..解：（1）抛物线y2＝2px（p＞0）的焦点为F（，0），准线与x轴的交点为E（﹣，0），当AB⊥x轴时，A的横坐标为，所以y A2＝2px A＝P2，所以|EA|＝＝＝2，解得p＝，所以抛物线的方程为y2＝2x；（2）设AB：x＝my+，A（x1，y1），B（x2，y2），联立抛物线的方程y2＝2x，消去x，可得y2﹣2my﹣2＝0，则y1+y2＝2m，y1y2＝﹣2，直线AE的斜率为k AE＝，则AE的方程为y＝（x+），令x＝0，可得y＝•，即M（0，•），同理可得N（0，•），＝＝＝2（x1+）（x2+）＝2[x1x2+（x1+x2）+]＝2x1x2+（x1+x2）+1＝+（+）+1＝1+[（y1+y2）2﹣2y1y2]+1＝（y1+y2）2+4＝4m2+4≥4．（当m＝0时，取得等号）．即的取值范围为[4，+∞）．。

开始输出S结束i ≤8i ←3 N YS ←S +2i （第5题图） i ←i ＋2S ←4 2020年2020届江苏省苏州市某中学2017级高三三模考试数学试卷★祝考试顺利★ (含答案)一、填空题：本大题共14小题,每小题5分,共计70分．不需要写出解答过程,请把答案直接填在答题卡相应位置上．．．．．．．．． 1．已知集合{014}{2024}A B ==-，，，，，，,则A B = ． 2．已知复数3i1iz +=-,其中i 为虚数单位,则复数z 的模是 ． 3．抛物线216y x =的准线方程为 ．4．某市为了响应江苏省“农村人居环境整治的新实践”,调研农村环境整治情况,按地域将下辖的250个行政村分成A B C D ，，，四组,对应的行政村个数分别为257510050，，，,若用分层抽样抽取50个行政村,则B 组中应该抽取的行政村数为 ．5．执行如图所示的程序框图,输出的S 的值为 ．6．中国古典乐器一般按“八音”分类,如图,在《周礼·春官·大师》中按乐器的制造材料对乐器分类,分别为“金、石、木、土、革、丝、匏、竹” 八音,其中“土、匏、竹”为吹奏乐器,“金、石、木、革”为打击乐器,“丝”为弹拨乐器．现从“八音”中任取不同的“一音”,则不是吹奏乐器的概率为 ． 7．已知函数2log (3)0,()302x x f x x x -<⎧⎪=⎨-⎪⎩，，≥，若1()2f a =,则实数a 的值是 ．8．已知{}n a 和{}n b 均为等差数列,若276a b +=,459a b +=,则63a b +的值是 ．9．已知12x x ，为函数()e sin x f x x =的两个极值点,则12||x x -的最小值为 ． 10．在长方体1111ABCD A B C D -中,1443AB AD AA ===，，,若在长方体中挖去一个体积最大的圆柱,则此圆柱与原长方体的体积比为 ．11．在平面直角坐标系xOy 中,已知圆22:(3)(4)16C x y +++=,若对于直线10x my ++=（第6题图）上的任意一点P ,在圆C 上总存在Q 使π2PQC ∠=,则实数m 的取值范围为 ． 12．如图,在平行四边形ABCD中,323AB AD BAD π==∠=，，,E 为BC 的中点,若线段DE 上存在一点M 满足1 ()3AM AB mAD m =+∈R ,则AM BD ⋅的值是 ．13．在ABC △中,设角A B C ，，对应的边分别为a b c ，，,记ABC △的面积为S ,若tan 2tan A B =,14．已知函数3()3 (0)f x x ax a =->,其图象记为曲线C ,曲线C 上存在异于原点的点0P ,使得曲线C 与其在0P 的切线交于另一点1P ,曲线C 与其在1P 的切线交于另一点2P ,若直线01P P 与直线02P P 的斜率之积小于9-,则a 的取值范围为 ．二、解答题：本大题共6小题,共计90分．请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）已知平面向量(2cos 1)θ=，a ,(13sin )θ=，b ． （1）若∥a b ,求sin 2θ的值； （2）若⊥a b ,求tan()4θπ+的值．16．（本小题满分14分）如图,在三棱锥P ABC -中,BC ⊥平面PAB ．已知PA AB =,D E ，分别为PB BC ，的中点． （1）求证：AD ⊥平面PBC ； （2）若点F 在线段AC 上,且12AF FC =, 求证：AD ∥平面PEF ．（第12题图）。

第二学期阶段性检测（二）高 三 数 学班级：高三( )班 姓名： 成绩：一、填空题：本大题共14个小题，每小题5分，共70分. 请把答案写在答题卡相应位置上.1. 设集合2{1}A x x =<，集合{02}B x x =<<，则A B =U ▲ ．【答案】(1,2)-【解析】集合A ＝{11}x x -<<，所以，A B =U (1,2)- 2. 设复数z 满足(1i)i z -=(i 为虚数单位)，则z = ▲ ．【解析】(1)111222i i i z i i +===-+-。

所以，||z == 3. 某高中高一、高二、高三年级的学生人数之比为8∶8∶9，现用分层抽样的方法从该校三个年级的学生中抽取容量为50的样本，则应从高二年级抽取 ▲ 名学生． 【答案】16【解析】依题意，设高一、高二、高三年级的学生人数为8x ，8x ，9x ， 则抽取的比例为：502889x x x x=++，所以，应从高二年级抽取学生人数：28x x⨯＝16 4. 从长度为2、4、5、6的四条线段中任选三条，能构成三角形的概率为 ▲ ． 【答案】34【解析】从长度为2、4、5、6的四条线段中任选三条，共有：34C ＝4种可能， 能构成三角形的有：（2、4、5），（2、5、6），（4、5、6），3组， 故所求的概率为：P ＝345. 已知一个算法的流程图如右图，则输出的结果S 的值是 ▲ ．【答案】11【解析】第1步：S ＝2S ＋n ＝1，n ＝n ＋1＝2； 第2步：S ＝2S ＋n ＝4，n ＝n ＋1＝3；第1步：S ＝2S ＋n ＝11，n ＝n ＋1＝4＞3，退出循环，输出S ＝11。

6. 在平面直角坐标系xOy 中，已知点F 为抛物线24y x =的焦点，则点F 到双曲线221916x y -=的渐近线的距离为 ▲ ． 【答案】45【解析】物线24y x =的焦点为F （1,0），双曲线221916x y -=的渐近线为：43y x =±，即：430x y ±-=距离d 224543=+ 7. 设实数x ，y 满足0 0 3 25 x y x y x y ≤≤≥⎧⎪≥⎪⎨+⎪⎪+⎩，，，，则4z x y =+的最大值是 ▲ ． 【答案】10【解析】不等式组表示的平面区域如下图： 目标函数4z x y =+过点C （52，0）时，取得最大值为10。

连云港市2017届高三年级模拟考试数学Ⅰ第Ⅰ卷（共70分）一、填空题(每题5分,满分70分,江答案填在答题纸上)1.已知集合}211{，，-=A,}7,210{，，=B,则集合BA 中元素的个数为．2.设a,Rb∈，biaii+=-+11(i为虚数单位)，则b的值为．3.在平面直角坐标系xOy中,双曲线13422=-yx的离心率是．4.现有三张识字卡片,分别写有“中”、“国”、“梦”这三个字.将这三张卡片随机排序，则能组成“中国梦”的概率是．5.如图是一个算法的流程图，则输出的k的值为．6.已知一组数据3，6，9，8，4，则该组数据的方差是．7.已知实数x，y满足⎪⎩⎪⎨⎧≥+≤-≤,2,3,1yxxxy则xy的取值范围是．8.若函数)2sin(2)(ϕ+=xxf)20(πϕ<<的图象过点)3,0(，则函数)(xf在],0[π上的单调减区间是．9.在公比为q且各项均为正数的等比数列}{na中，nS为}{na的前n211qa=，且225+=SS，则q的值为．10.如图，在正三棱柱111CBAABC-中，已知31==AAAB，点P在棱1CC上，则三棱锥1ABAP-的体积为 ．11.如图，已知正方形ABCD 的边长为2，BC 平行于x 轴，顶点A ，B 和C 分别在函数x y a log 31=，x y a log 22=和)1(log 3>=a x y a 的图象上，则实数a 的值为 ．),5()1,(+∞-∞∈ x ，都有0)2(22>+--a x a x ，则实数a 的取值范围是 ．13.在平面直角坐标系xOy 中，圆C ：3)()2(22=-++m y x .若圆C 存在以G 为中点的弦AB ，且GO AB 2=，则实数m 的取值范围是 ．14.已知ABC ∆三个内角A ，B ，C 的对应边分别为a ，b ，c ，且3π=C ，2=c ，当ABAC •取得最大值时，ab的值为 ． 第Ⅱ卷（共90分）二、解答题 （本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤.）15.如图，在ABC ∆中，已知点D 在边AB 上，DB AD 3=，54cos =A ，135cos =∠ACB ，13=BC .（1）求B cos 的值； （2）求CD 的长.16.如图，在四棱锥ABCD P -中，底面ABCD 是矩形，点E 在棱PC 上（异于点P ，C ），平面ABE 与棱PD 交于点F .（1）求证：EF AB //；（2）若平面⊥PAD 平面ABCD ，求证：EF AE ⊥.17. 如图，在平面直角坐标系xOy 中，已知椭圆C ：13422=+y x 的左、右顶点分别为A ，B ，过右焦点F 的直线l 与椭圆C 交于P ，Q 两点（点P 在x 轴上方）.（1）若FP QF 2=，求直线l 的方程；（2）设直线AP ，BQ 的斜率分别为1k ，2k ，是否存在常数λ，使得21k k λ=？若存在，求出λ的值；若不存在，请说明理由.18. O 的圆心与矩形ABCD 对角线的交点重合，且圆与矩形上下两边相切（E 为上切点），与左右两边相交（F ，G m ，且21≥AD AB ，设θ=∠EOF ，透光区域的面积为S .（1）求S 关于θ的函数关系式，并求出定义域；（2）根据设计要求，透光区域与矩形窗面的面积比值越大越好.当该比值最大时，求边AB 的长度.19. 已知两个无穷数列}{n a 和}{n b 的前n 项和分别为n S ，n T ，11=a ，42=S ，对任意的*∈N n ，都有n n n n a S S S ++=++2123. （1）求数列}{n a 的通项公式；（2）若}{n b 为等差数列，对任意的*∈N n ，都有n n T S >.证明：n n b a >； （3）若}{n b 为等比数列，11a b =，22a b =，求满足)(22*∈=++N k a S b T a k nn nn 的n 值.20. 已知函数)0(ln )(>+=m x x xmx f ，2ln )(-=x x g . （1）当1=m 时，求函数)(x f 的单调区间；（2）设函数2)()()(--=x xg x f x h ，0>x .若函数))((x h h y =的最小值是223，求m 的值； （3）若函数)(x f ，)(x g 的定义域都是],1[e ，对于函数)(x f 的图象上的任意一点A ，在函数)(x g 的图象上都存在一点B ，使得OB OA ⊥，其中e 是自然对数的底数，O 为坐标原点，求m 的取值范围.21.【选做题】本题包括A 、B 、C 、D 四小题，请选定其中两题，并在相应的答题区域内作答，若多做，则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.选修4-1：几何证明选讲如图，圆O 的弦AB ，MN 交于点C ，且A 为弧MN 的中点，点D 在弧BM 上，若ADB ACN ∠=∠3，求ADB ∠的度数.B.选修4-2：矩阵与变换已知矩阵⎥⎦⎤⎢⎣⎡=daA23，若⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=4821A，求矩阵A的特征值.C.选修4-4：坐标系与参数方程在极坐标系中，已知点)2,2(πA，点B在直线l：)20(0sincosπθθρθρ≤≤=+上，当线段AB 最短时，求点B的极坐标.D.选修4-5：不等式选讲已知a，b，c为正实数，且222333cbacba=++，求证：333≥++cba.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程在平面直角坐标系xOy中，点)0,1(F，直线1-=x与动直线ny=的交点为M，线段MF的中垂线与动直线ny=的交点为P.（1）求动点P的轨迹E的方程；（2）过动点M作曲线E的两条切线，切点分别为A，B，求证：AMB∠的大小为定值. 23.选修4-5：不等式选讲已知集合},...,2,1{nU=)2,(≥∈*nNn，对于集合U的两个非空子集A，B，若∅=BA ，则称),(BA为集合U的一组“互斥子集”.记集合U的所有“互斥子集”的组数为)(nf（视),(BA 与),(AB为同一组“互斥子集”）.（1）写出)2(f，)3(f，)4(f的值；（2）求)(nf.三师2017届高三第三次质量检测参考答案与评分标准试一、填空题1.52. 13.27 4. 61 5.6 6. 526 (或5.2) 7. ]32,31[-(或3231≤≤-x y ) 8. )127,12(ππ(或]127,12[ππ) 9.215- 10. 34911. 2 12. ]5,1((或51≤<a )13. ]2,2[-(或22≤≤-m ) 14. 32+二、解答题15.解:(1)在ABC ∆中, 54cos =A , ),0(π∈A ， 所以=-=A A 2cos 1sin 53)54(12=-. 同理可得, 1312sin =∠ACB . 所以=∠+-=)](cos[cos ACB A B π)cos(ACB A ∠+-ACB A ACB A ∠-∠=cos cos sin sin6416135********=⨯-⨯=. (2)在ABC ∆中,由正弦定理得, BBC AB sin =2013125313sin =⨯=∠ACB .又DB AD 3=,所以541==AB BD . 在BCD ∆中,由余弦定理得, B BC BD BC BD CD cos 222•-+=6416135213522⨯⨯⨯-+= 29=.16. 解:(1) 因为ABCD 是矩形，所以CD AB //． 又因为⊄AB 平面PDC ，⊂CD 平面PDC ， 所以//AB 平面PDC ．又因为⊂AB 平面ABEF ，平面 ABEF 平面EF PDC =， 所以EF AB //．（2）因为ABCD 是矩形，所以AD AB ⊥．又因为平面⊥PAD 平面ABCD ，平面 PAD 平面AD ABCD =，⊂AB 平面ABCD ，所以⊥AB 平面PAD ．又⊂AF 平面PAD ，所以AF AB ⊥． 又由（1）知EF AB //，所以EF AF ⊥．17. 解:(1) 因为42=a ，32=b ，所以122=-=b a c ，所以F 的坐标为（1,0），设),(11y x P ，),(22y x Q ，直线l 的方程为1+=my x ，代入椭圆方程，得096)34(22=-++my y m ，则22134163m m m y +++-=，22234163mm m y ++--=． 若PF QF 2=，则0341632341632222=+++-⨯+++--m m m m m m ， 解得552=m ，故直线l 的方程为0525=--y x ． （2）由（1）知，221346m m y y +-=+，221349my y +-=， 所以)(2334921221y y m m y my +=+-=， 所以22112122y x x y k k --+=)3()1(1221+-=my y my y 313)(23)(23221121=++-+=y y y y y y ，故存在常数31=λ，使得2131k k =． 18. 解:(1) 过点O 作FG OH ⊥于点H ，则θ=∠=∠EOF OFH ， 所以θθsin sin ==OF OH ，θθcos cos ==OF FH ．所以OEF OFH S S S 扇形44+=∆)21(4cos sin 2θθθ⨯+=θθ22sin +=，因为21≥AD AB ，所以21sin ≥θ，所以定义域为)2,6[ππ．（2）矩形窗面的面积为θθsin 4sin 22=⨯=•=AB AD S 矩形． 则透光区域与矩形窗面的面积比值为θθθθθθθsin 22cos sin 42cos sin 2+=+．设θθθθsin 22cos )(+=f ，26πθπ<≤． 则θθθθθθ2sin 2cos sin sin 21)(-+='f θθθθθ23sin 2sin cos sin --= θθθθθ22sin 2cos cos sin -= θθθθ2sin 2)2sin 21(cos -=， 因为26πθπ<≤，所以212sin 21≤θ，所以02sin 21<-θθ，故0)(<'θf ， 所以函数)(θf 在)2,6[ππ上单调减． 所以当6πθ=时，)(θf 有最大值436+π，此时)(1sin 2m AB ==θ 答：（1）S 关于θ的函数关系式为θθ22sin +=S ，定义域为)2,6[ππ；（2）透光区域与矩形窗面的面积比值最大时，AB 的长度为1m ． 19. 解:(1) 由n n n n a S S S ++=++2123，得n n n n n a S S S S +-=-+++121)(2， 即n n n a a a +=++212，所以n n n n a a a a -=-+++112． 由11=a ，41=S ，可知32=a ．所以数列}{n a 是以1为首项，2为公差的等差数列． 故}{n a 的通项公式为12-=n a n ．（2）证法一：设数列}{n b 的公差为d ，则d n n nb T n 2)1(1-+=， 由（1）知，2n S n =．因为n n T S >，所以d n n nb n 2)1(12-+>，即02)2(1>-+-b d n d 恒成立， 所以⎩⎨⎧>-≥-,02,021b d d 即⎩⎨⎧<≤,2,21d b d 又由11T S >，得11<b ，所以d n b n b a n n )1(121----=-11)2(b d n d --+-=11)2(b d d --+-≥011>-=b ． 所以n n b a >，得证．证法二：设}{n b 的公差为d ，假设存在自然数20≥n ，使得00n n b a >， 则≤⨯-+2)1(01n a d n b )1(01-+，即)2)(1(011--≤-d n b a ， 因为11b a >，所以2>d ． 所以212)1(n d n n nb S T n n --+=-n db n d )2()12(12-+-=， 因为012>-d，所以存在*∈N N n 0，当0n N n >时，0>-n n S T 恒成立． 这与“对任意的*∈N n ，都有T S n >”矛盾！ 所以n n b a >，得证．（3）由（1）知，2n S n =．因为}{n b 为等比数列，且11=b ，32=b ，所以}{n b 是以1为首项，3为公比的等比数列． 所以13-=n n b ，213-=n n T ．则2123131222nn S b T a n n n n n n +-+-=++-2123223n n n n +-+=-212232263n n n n ++--=-， 因为*∈N n ，所以02262>+-n n ，所以322<++nn nn S b T a ．而12-=k a k ，所以122=++nn nn S b T a ，即01321=-+--n n n （*）．当2,1=n 时，（*）式成立； 当2≥n 时，设13)(21-+-=-n n n f n ，则n n n f n f n++-=-+2)1(3)()1(0)3(2)13(121>-=-+----n n n n n ，所以...)(...)3()2(0<<<<=n f f f ． 故满足条件的n 的值为1和2． 20. 解:(1) 当1=m 时，x x x x f ln 1)(+=，1ln 1)(2++='x xx f ． 因为)(x f '在),0(+∞上单调增，且0)1(='f ，所以当1>x 时，0)(>'x f ；当10<<x 时，0)(<'x f ． 所以函数)(x f 的单调增区间是),1(+∞．（2）22)(-+=x xmx h ，则22222)(x m x x m x h -=-='，令0)(='x h 得2m x =，当20m x <<时，0)(<'x h ，函数)(x h 在)2,0(m 上单调减； 当2m x >时，0)(>'x h ，函数)(x h 在),2(+∞m 上单调增． 所以222)2()]([min -==m m h x h ． ①当2)12(2m m ≥-，即94≥m 时， 函数))((x h h y =的最小值)12(2[2)222(-=-m m m h 223]1)12(2=--+m ， 即092617=+-m m ，解得1=m 或179=m （舍），所以1=m ； ②当2)12(20m m <-<，即9441<<m 时， 函数))((x h h y =的最小值223)12(2)2(=-=m m h ，解得54=m （舍）． 综上所述，m 的值为1．（3）由题意知，x x m k OA ln 2+=，xx k OB 2ln -=． 考虑函数x x y 2ln -=，因为2ln 3xx y -='在],1[e 上恒成立， 所以函数x x y 2ln -=在],1[e 上单调增，故]1,2[ek OB --∈． 所以],21[e k OA ∈，即e x x m ≤+≤ln 212在],1[e 上恒成立， 即)ln (ln 2222x e x m x x x -≤≤-在],1[e 上恒成立． 设x x x x p ln 2)(22-=，则0ln 2)(≤-='x x p 在],1[e 上恒成立， 所以)(x p 在],1[e 上单调减，所以21)1(=≥p m ． 设)ln ()(2x e x x q -=，则≥--=')ln 212()(x e x x q 0ln 212(>--e e x 在],1[e 上恒成立，所以)(x q 在],1[e 上单调增，所以e q m =≤)1(．综上所述，m的取值范围为],21[e．21.解：A．连结AN，DN．因为A为弧MN的中点，所以ADNANM∠=∠．而NDBNAB∠=∠，所以NDBADNNABANM∠+∠=∠+∠，即ADBBCN∠=∠．又因为ADBACN∠=∠3，所以︒=∠+∠=∠+∠1803ADBADBBCNACN，故︒=∠45ADB．B．因为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=212321daA⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡++=48226da，所以⎩⎨⎧=+=+42286da解得⎩⎨⎧==14da所以⎥⎦⎤⎢⎣⎡=1232A．所以矩阵A的特征多项式为1232)(---=λλλf436)1)(2(2--=---=λλλλ，令0)(=λf，解得矩阵A的特征值为11-=λ，42=λ．C．以极点为原点，极轴为x轴正半轴，建立平面直角坐标系，则点)2,2(πA的直角坐标为)2,0(，直线l的直角坐标方程为0=+yx．AB最短时，点B为直线02=+-yx与直线l的交点，解⎩⎨⎧=+=+-2yxyx得⎩⎨⎧=-=11yx所以点B的直角坐标为（-1,1）．所以点B的极坐标为)43,2(π．D．因为33332223333cbacbacba≥=++，所以3≥abc，所以33333≥≥++abccba，当且仅当33===c b a 时，取“”．22. 解:(1) 因为直线n y =与1-=x 垂直，所以MP 为点P 到直线1-=x 的距离． 连结PF ，因为P 为线段MF 的中垂线与直线n y =的交点，所以PF MP =． 所以点P 的轨迹是抛物线．焦点为)0,0(P ，准线为1-=x ．所以曲线E 的方程为x y 42=．（2）由题意，过点),1(n M -的切线斜率存在，设切线方程为)1(+=-x k n y ， 联立⎩⎨⎧=++=,4,2x y n k kx y 得04442=++-n k y ky ， 所以0)44(4161=+-=∆n k k ，即012=-+kn k （*），因为0422>+=∆n ，所以方程（*）存在两个不等实根，设为1k ，2k ， 因为121-=•k k ，所以︒=∠90AMB ，为定值．23. 解:(1) 1)2(=f ，6)3(=f ， 25)4(=f ．（2）解法一：设集合A 中有k 个元素，1,...,3,2,1-=n k ．则与集合A 互斥的非空子集有12--k n 个．于是)12(21)(11-=--=∑k n n k k n C n f ]2[211111∑∑-=--=-=n k k n k n n k k n C C ． 因为=--=∑k n n k k n C 211∑-=---1000222n k n n n n k n k n C C C 12312)12(--=--+=n n n n ， n n n n k k n n k kn C C C C--=∑∑-=-=0101122-=n ， 所以---=)123[(21)(n n n f )123(21)]22(1+-=-+n n n ． 解法二：任意一个元素只能在集合A ，B ，)(B A C C U =之一中，则这n 个元素在集合A ，B ，C 中，共有n 3种；其中A 为空集的种数为n 2，B 为空集的种数为n2，所以A ，B 均为非空子集的种数为1223+⨯-n n ， 又),(B A 与),(A B 为同一组“互斥子集”，所以)123(21)(1+-=+n n n f ．。

2020届江苏省扬州市新华中学2017级高三下学期3月月考数学试卷★祝考试顺利★(解析版)一、填空题,本大题共14个小题,每小题5分,共70分.请把答案写在答题卡相应位置上.1.函数πsin 23y x ⎛⎫=- ⎪⎝⎭最小正周期_______． 【答案】π【解析】 函数πsin 23y x ⎛⎫=- ⎪⎝⎭的最小正周期为222T πππω=== 2.函数2()2(3)1f x x a x =+-+在区间(,3)-∞-上递减,则实数a 的取值范围是_____【答案】{}6|a a ≤【解析】根据二次函数开口方向,对称轴以及在区间上的单调性列不等式,解不等式求得a 的取值范围.【详解】∵f (x )=x 2+2(a ﹣3)x +1,在区间(﹣∞,﹣3)上递减,开口向上,且对称轴3x a =-, ∴3﹣a ≥﹣3,解得,a ≤6故答案为:{}6|a a ≤.3.已知焦点在x 轴上的双曲线的渐近线方程为340±=x y ,则双曲线的离心率为____.【答案】54【解析】焦点在x 轴上的双曲线的渐近线方程为34y x ,可知34b a,由此可求出双曲线的离心率． 【详解】由题可设焦点在x 轴上的双曲线方程为22221(,0)x y a b a b -=>, 由于该双曲线的渐近线方程为34yx ,则34b a ,在双曲线中222c a b =+,所以双曲线的离心率2223511()44c b e a a ==+=+=, 故双曲线的离心率为54． 4.已知函数()x x ax f x xe e=-（其中e 为自然对数的底数）为偶函数,则实数a 的值为____． 【答案】1【解析】利用()()f x f x =-恒成立可得实数a 的值．【详解】因为()f x 为偶函数,所以()()f x f x =-恒成立即()x x x xa x ax xe xe e e ----=--,整理得到()x x x x e e a e e --+=+恒成立, 故1a =,填1.【点睛】含参数的偶函数（或奇函数）,可通过取自变量的特殊值来求参数的大小,注意最后检验必不可少,也可以利用()()f x f x =-（或()()f x f x -=-）恒成立来求参数的大小.5.在ABC 中,点D E ，分别在边AB BC ，上,且2AD DB BE EC ＝，＝,记,AB a AC b ==,若DE xa yb =+则x y +的值为_____.【答案】12【解析】利用平面向量加法、减法和数乘的运算,将DE 转化为以,a b 为基底的表现形式,根据平面向量的基本定理求得,x y 的值,由此求得x y +的值.【详解】如图,∵AD =DB ,BE =2EC ;。

2017-2018学年江苏省泰州市姜堰区高三（下）期初数学试卷一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）1．设U=R，A={x|x＜1}则∁U A=．2．计算i+i3=（i为虚数单位）．3．一个单位共有职工200人，其中不超过45岁的有120人，超过45岁的有80人．为了调查职工的健康状况，用分层抽样的方法从全体职工中抽取一个容量为25的样本，应抽取超过45岁的职工人．4．如图是一个算法的流程图，最后输出的S=．5．若以连续掷两次骰子得到的点数m，n分别作为点P的横、纵坐标，则点P在直线x+y=4上的概率为．6．函数f（x）=2sinx+3cosx的极大值为．7．抛物线y2=4x上任一点到定直线l：x=﹣1的距离与它到定点F的距离相等，则该定点F 的坐标为．8．等差数列{a n}的前n项和记为S n，满足2n=，则数列{a n}的公差d=．9．函数f（x）=e x可以表示成一个奇函数g（x）与一个偶函数h（x）之和，则g（x）=．10．圆C过点A（2，0），B（4，0），直线l过原点O，与圆C交于P，Q两点，则•=．11．已知非零向量，，满足x2++=，x∈R．记△=2﹣4，下列说法正确的是．（只填序号）①若△=0，则x有唯一解；②若△＞0，则x有两解；③若△＜0，则x无解．12．定义在R上的奇函数f（x）满足f（x+4）=f（x），且在[0，2]上的解析式为f（x）=，则f（）+f（）=．13．把正整数按一定的规则排成了如图所示的三角形数表，设a ij（i，j∈N*）是位于这个三角形数表中从上往下数第i行，从左往右数第j个数，如a42=8，若a ij=2015，则i+j= ．14．在平行四边形ABCD中，∠BAD=60°，AB=1，AD=，P为平行四边形内一点，且AP=，若（λ，μ∈R），则λ+μ的最大值为．二、解答题：（本大题共6小题，共90分．解答应写出文字说明，证明过程或演算步骤．）15．如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD=DC，点E是PC的中点，作EF⊥PB交PB于点F．（1）求证：PA∥平面BDE；（2）求证：PB⊥平面DEF．16．设△ABC的内角A、B、C的对边分别为a、b、c，a=btanA，且B为钝角．（Ⅰ）证明：B﹣A=；（Ⅱ）求sinA+sinC的取值范围．17．已知数列{a n}为等差数列，首项a1=5，公差d=﹣1，数列{b n}为等比数列，b2=1，公比为q（q＞0），c n=a n b n，S n为{c n}的前n项和，记S n=c1+c2+..+c n．（Ⅰ）求b1+b2+b3的最小值；（Ⅱ）求S10；（Ⅲ）求出使S n取得最大的n的值．18．已知美国苹果公司生产某款iphone手机的年固定成本为40万美元，每生产1只还需另投入16美元．设苹果公司一年内共生产该款iphone手机x万只并全部销售完，每万只的销售收入为R（x）万美元，且R（x）=（1）写出年利润W（万元）关于年产量x（万只）的函数解析式；（2）当年产量为多少万只时，苹果公司在该款手机的生产中所获得的利润最大？并求出最大利润．19．在平面直角坐标系xOy 中，离心率为的椭圆C： +=1（a＞b＞0）的左顶点为A，且A到右准线的距离为6，点P、Q是椭圆C上的两个动点．（1）求椭圆的标准方程；（2）如图，当P、O、Q共线时，直线PA，QA分别与y轴交于M，N两点，求证：•定值；（3）设直线AP，AQ的斜率分别为k1，k2，当k1•k2=﹣1时，证明直线PQ经过定点R．20．已知函数f（x）=lnx．（1）方程f（x+a）=x有且只有一个实数解，求a的值；（2）若函数的极值点x1，x2（x1＜x2）恰好是函数h（x）=f（x）﹣cx2﹣bx的零点，求的最小值．[几何证明选讲]（共1小题，满分0分）21．如图，A、B、C、D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC=ED．（Ⅰ）证明：CD∥AB；（Ⅱ）延长CD到F，延长DC到G，使得EF=EG，证明：A、B、G、F四点共圆．[矩阵与变换]（共1小题，满分0分）22．已知矩阵A=．（1）求A的逆矩阵A﹣1；（2）求矩阵A的特征值λ1、λ2和对应的一个特征向量、．五、[坐标系与参数方程选讲]（共1小题，满分0分）23．已知在直角坐标系x0y内，直线l的参数方程为（t为参数）．以Ox为极轴建立极坐标系，圆C的极坐标方程为．（1）写出直线l的普通方程和圆C的直角坐标方程；（2）判断直线l和圆C的位置关系．[不等式选讲]（共1小题，满分0分）24．设x，y，z∈R+，求证：．七、必考题（共2小题，满分0分）25．如图，四棱锥P﹣ABCD的底面为矩形，PA是四棱锥的高，PB与DC所成角为45°，F 是PB的中点，E是BC上的动点．（Ⅰ）证明：PE⊥AF；（Ⅱ）若BC=2BE=2AB，求直线AP与平面PDE所成角的大小．．26．已知抛物线C：y2=2px（p＞0）的焦点为F，直线y=4与y轴的交点为P，与C的交点为Q，且|QF|=|PQ|．（Ⅰ）求C的方程；（Ⅱ）过F的直线l与C相交于A、B两点，若AB的垂直平分线l′与C相交于M、N两点，且A、M、B、N四点在同一圆上，求l的方程．2015-2016学年江苏省泰州市姜堰区高三（下）期初数学试卷参考答案与试题解析一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）1．设U=R，A={x|x＜1}则∁U A={x|x≥1} ．【考点】补集及其运算．【分析】根据全集U及A，求出A的补集即可．【解答】解：∵U=R，A={x|x＜1}，∴∁U A={x|x≥1}，故答案为：{x|x≥1}2．计算i+i3=0（i为虚数单位）．【考点】复数代数形式的混合运算．【分析】直接利用虚数单位i的运算性质得答案．【解答】解：i+i3=i﹣i=0．故答案为：0．3．一个单位共有职工200人，其中不超过45岁的有120人，超过45岁的有80人．为了调查职工的健康状况，用分层抽样的方法从全体职工中抽取一个容量为25的样本，应抽取超过45岁的职工10人．【考点】分层抽样方法．【分析】本题是一个分层抽样，根据单位共有职工200人，要取一个容量为25的样本，得到本单位每个职工被抽到的概率，从而知道超过45岁的职工被抽到的概率，得到结果．【解答】解：本题是一个分层抽样，∵单位共有职工200人，取一个容量为25的样本，∴依题意知抽取超过45岁的职工为．故答案为：10．4．如图是一个算法的流程图，最后输出的S=25．【考点】循环结构．【分析】按照程序框图的流程，写出前几次循环的结果，并判断每个结果是否满足判断框中的条件，直到不满足条件，输出s．【解答】解：经过第一次循环得到的结果为s=9，a=2，P=9，经过第二次循环得到的结果为s=16，a=3，P=16，经过第三次循环得到的结果为s=21，a=4，P=21，经过第四次循环得到的结果为s=24，a=5，P=21，经过第五次循环得到的结果为s=25，a=6，P=25，经过第六次循环得到的结果为s=24，a=7，此时满足判断框中的条件输出25故答案为25．5．若以连续掷两次骰子得到的点数m，n分别作为点P的横、纵坐标，则点P在直线x+y=4上的概率为．【考点】列举法计算基本事件数及事件发生的概率．【分析】由题意知本题是一个古典概型，由列举法可得P的情况数目，满足条件的事件是点P在直线x+y=4上，即两个数字之和是4，可以列举出P的情况数目，根据古典概型概率公式得到概率．【解答】解：根据题意，以连续掷两次骰子得到的点数m，n分别作为点P的横、纵坐标，则P的情况有（1，1）、（1，2）、（1，3）、（1，4）、（1，5）、（1，6）、（2，1）、（2，2）、（2，3）、（2，4）、（2，5）、（2，6）、（3，1）、（3，2）、（3，3）、（3，4）、（3，5）、（3，6）、（4，1）、（4，2）、（4，3）、（4，4）、（4，5）、（4，6）、（5，1）、（5，2）、（5，3）、（5，4）、（5，5）、（5，6）、（6，1）、（6，2）、（6，3）、（6，4）、（6，5）、（6，6），共36种；点P在直线x+y=4上，即两个数字之和是4，有（1，3）（2，2）（3，1）；共有3种结果，则点P在直线x+y=4上的概率为=；故答案为．6．函数f（x）=2sinx+3cosx的极大值为．【考点】三角函数的化简求值．【分析】利用两角和与差的三角函数化简函数的表达式为一个角的一个三角函数的形式，然后求解即可．【解答】解：函数f（x）=2sinx+3cosx=sin（x+θ），其中tanθ=．sin（x+θ）．故答案为：．7．抛物线y2=4x上任一点到定直线l：x=﹣1的距离与它到定点F的距离相等，则该定点F 的坐标为（1，0）．【考点】抛物线的简单性质．【分析】由抛物线的定义，可得定点F为抛物线的焦点，求出抛物线y2=4x的焦点坐标，即可得出结论．【解答】解：由抛物线的定义，可得定点F为抛物线的焦点，∵抛物线y2=4x的焦点坐标为（1，0），∴定点F的坐标为（1，0）．故答案为：（1，0）．8．等差数列{a n}的前n项和记为S n，满足2n=，则数列{a n}的公差d=8．【考点】等差数列的通项公式．【分析】由已知得S n=4n2﹣n，由此能求出数列{a n}的公差d．【解答】解：∵等差数列{a n}的前n项和记为S n，满足2n=，∴S n=4n2﹣n，∴a1=S1=4﹣1=3，a2=S2﹣S1=（4×4﹣2）﹣（4﹣1）=11，∴数列{a n}的公差d=11﹣3=8．故答案为：8．9．函数f（x）=e x可以表示成一个奇函数g（x）与一个偶函数h（x）之和，则g（x）=．【考点】函数解析式的求解及常用方法；函数奇偶性的性质．【分析】由题意可得f（x）=e x =g（x）+h（x）①，其中，g（x）为奇函数，h（x）为偶函数，则有e﹣x =g（﹣x）+h（﹣x）=﹣g（x）+h（x）②，由①②求得g（x）的解析式．【解答】解：由题意可得f（x）=e x =g（x）+h（x）①，其中，g（x）为奇函数，h（x）为偶函数，则有e﹣x =g（﹣x）+h（﹣x）=﹣g（x）+h（x）②，把①﹣②可得：g（x）=，故答案为：．10．圆C过点A（2，0），B（4，0），直线l过原点O，与圆C交于P，Q两点，则•= 8．【考点】直线与圆的位置关系．【分析】由题意，圆看成是圆外一点（原点0）向圆作两条交线．根据割线定理即可得到答案．【解答】解：由题意：圆C过点A（2，0），B（4，0），相当于圆与直线AB相交，∴|OA|=2，|OB|=4直线l过原点O，与圆C交于P，Q两点，即为圆外一点（原点0）向圆作两条割线AB与PQ．∵O，P，Q三点在一条直线上，夹角为0，cos0=，∴•=|OQ|•|OP|，由圆的割线定理知：|OQ|•|OP|=|OA|•|OB|=8，所以：•=8，故答案为：8．11．已知非零向量，，满足x2++=，x∈R．记△=2﹣4，下列说法正确的是③．（只填序号）①若△=0，则x有唯一解；②若△＞0，则x有两解；③若△＜0，则x无解．【考点】平面向量数量积的运算．【分析】根据题意，利用向量，表示向量，代入计算△=2﹣4，讨论△=0、△＞0和△＜0时x解的情况，从而判断出正确的．【解答】解：∵非零向量，，满足x2++=，x∈R，∴=﹣x2﹣，∴△=2﹣4=+4（x2+）=+4x2+4•；当△=0时， +4x2+4•=0∴x2=﹣，+4•＞0时x无解，+4•＜0时x有2解，+4•=0时x有1解，故①错误；当△＞0时， +4x2+4•＞0∴x2＞﹣，x有无数解，故②错误；当△＜0时， +4x2+4•＜0∴x2＜﹣，x无解，故③正确．综上，正确的是③．故答案为：③．12．定义在R上的奇函数f（x）满足f（x+4）=f（x），且在[0，2]上的解析式为f（x）=，则f（）+f（）=．【考点】分段函数的应用．【分析】根据函数的奇偶性和周期性，以及分段函数的表达式代入即可得到结论．【解答】解：由f（x+4）=f（x），得函数的周期是4，则f（）=f（8﹣）=f（﹣），∵f（x）是奇函数，∴，f（﹣）=﹣f（）=﹣×=﹣，f（）=f（8﹣）=f（﹣）=﹣f（）=﹣sin=sin，则f（）+f（）=﹣=，故答案为：．13．把正整数按一定的规则排成了如图所示的三角形数表，设a ij（i，j∈N*）是位于这个三角形数表中从上往下数第i行，从左往右数第j个数，如a42=8，若a ij=2015，则i+j=110 ．【考点】归纳推理．【分析】通过观察给出的三角形数表，找到如下规律，奇数行都是奇数，偶数行都是偶数，且每一行的数的个数就是行数，然后根据2015是第1008个奇数，利用等差数列的前n项和公式分析出它所在的行数，再利用等差数列的通项公式求其所在的列数，则i与j的和可求．【解答】解：由三角形数表可以看出其奇数行中的数都是奇数，偶数行中的数都是偶数，2015=2×1008﹣1，所以2015为第1008个奇数，又每一行中奇数的个数就是行数，又前31个奇数行内奇数的个数的和为31×=961，即第31个奇数行的最后一个奇数是961×2﹣1=1921，前32个奇数行内奇数的个数的和为32×1+=1024，故2015在第32个奇数行内，所以i=63，因为第63行的第一个数为1923，则2015=1923+2（m﹣1），所以m=47，即j=47，所以i+j=63+47=110．故答案为：110．14．在平行四边形ABCD中，∠BAD=60°，AB=1，AD=，P为平行四边形内一点，且AP=，若（λ，μ∈R），则λ+μ的最大值为1．【考点】平面向量数量积的运算．【分析】利用数量积定义及其运算性质、不等式的性质即可得出．【解答】解：∵，∴，即，又AB=1，，∠BAD=60°，∴，∴=λ2+3μ2+，∴=≤，∴≤1，∴的最大值为1，当且仅当，取等号．故答案为：1．二、解答题：（本大题共6小题，共90分．解答应写出文字说明，证明过程或演算步骤．）15．如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD=DC，点E是PC的中点，作EF⊥PB交PB于点F．（1）求证：PA∥平面BDE；（2）求证：PB⊥平面DEF．【考点】直线与平面垂直的判定；直线与平面平行的判定．【分析】（1）连结AC，设AC交BD于O，连结EO，则PA∥EO，由此能证明PA∥平面EO．（2）由已知得PD⊥BC，CD⊥BC，从而BC⊥平面PDC，进而BC⊥DE，再由DE⊥PC，DE⊥PB，由此能证明PB⊥平面DEF．【解答】证明：（1）连结AC，设AC交BD于O，连结EO，∵底面ABCD中矩形，∴点O是AC的中点，又∵点E是PC的中点，∴PA∥EO，∵EO⊂平面BDE，PA⊄平面BDE，∴PA∥平面EO．（2）PD⊥底面ABCD，BC⊂底面ABCD，∴PD⊥BC，∵底面ABCD中矩形，∴CD⊥BC，∵PD∩CD=D，∴BC⊥平面PDC，∵DE⊂平面PDC，∴BC⊥DE，∵PD=DC，E是PC的中点，∴DE⊥PC，∵PC∩BC=C，∴DE⊥PB，又∵EF⊥PB，DE∩EF=E，DE⊂平面DEF，EF⊂平面DEF，∴PB⊥平面DEF．16．设△ABC的内角A、B、C的对边分别为a、b、c，a=btanA，且B为钝角．（Ⅰ）证明：B﹣A=；（Ⅱ）求sinA+sinC的取值范围．【考点】正弦定理．【分析】（Ⅰ）由题意和正弦定理可得sinB=cosA，由角的范围和诱导公式可得；（Ⅱ）由题意可得A∈（0，），可得0＜sinA＜，化简可得sinA+sinC=﹣2（sinA﹣）2+，由二次函数区间的最值可得．【解答】解：（Ⅰ）由a=btanA和正弦定理可得==，∴sinB=cosA，即sinB=sin（+A）又B为钝角，∴+A∈（，π），∴B=+A，∴B﹣A=；（Ⅱ）由（Ⅰ）知C=π﹣（A+B）=π﹣（A++A）=﹣2A＞0，∴A∈（0，），∴sinA+sinC=sinA+sin（﹣2A）=sinA+cos2A=sinA+1﹣2sin2A=﹣2（sinA﹣）2+，∵A∈（0，），∴0＜sinA＜，∴由二次函数可知＜﹣2（sinA﹣）2+≤∴sinA+sinC的取值范围为（，]17．已知数列{a n}为等差数列，首项a1=5，公差d=﹣1，数列{b n}为等比数列，b2=1，公比为q（q＞0），c n=a n b n，S n为{c n}的前n项和，记S n=c1+c2+..+c n．（Ⅰ）求b1+b2+b3的最小值；（Ⅱ）求S10；（Ⅲ）求出使S n取得最大的n的值．【考点】数列的求和．【分析】（I）b1+b2+b3=q﹣1+1+q，（q＞0），利用基本不等式的性质即可得出最小值．（II）由题意知：，可得，利用“错位相减法”、等比数列的求和公式即可得出．（III）令，解得n即可得出．【解答】解：（I）b1+b2+b3=q﹣1+1+q≥2+1=3，（q＞0），∴最小值为3．（II）由题意知：，∴，，，∴，当q=1 时，S10=5．当q≠1 时，（1﹣q）S10=，．（III）令，解得：n≤6，∴n取5或6时，S n最大．18．已知美国苹果公司生产某款iphone手机的年固定成本为40万美元，每生产1只还需另投入16美元．设苹果公司一年内共生产该款iphone手机x万只并全部销售完，每万只的销售收入为R（x）万美元，且R（x）=（1）写出年利润W（万元）关于年产量x（万只）的函数解析式；（2）当年产量为多少万只时，苹果公司在该款手机的生产中所获得的利润最大？并求出最大利润．【考点】函数与方程的综合运用．【分析】（1）利用利润等于收入减去成本，可得分段函数解析式；（2）分段求出函数的最大值，比较可得结论．【解答】解：（1）利用利润等于收入减去成本，可得当0＜x≤40时，W=xR（x）﹣（16x+40）=﹣6x2+384x﹣40；当x＞40时，W=xR（x）﹣（16x+40）=∴W=；（2）当0＜x≤40时，W=﹣6x2+384x﹣40=﹣6（x﹣32）2+6104，∴x=32时，W max=W（32）=6104；当x＞40时，W=≤﹣2+7360，当且仅当，即x=50时，W max=W（50）=5760∵6104＞5760∴x=32时，W的最大值为6104万美元．19．在平面直角坐标系xOy 中，离心率为的椭圆C： +=1（a＞b＞0）的左顶点为A，且A到右准线的距离为6，点P、Q是椭圆C上的两个动点．（1）求椭圆的标准方程；（2）如图，当P、O、Q共线时，直线PA，QA分别与y轴交于M，N两点，求证：•定值；（3）设直线AP，AQ的斜率分别为k1，k2，当k1•k2=﹣1时，证明直线PQ经过定点R．【考点】椭圆的简单性质．【分析】（1）由椭圆的离心率为，且A到右准线的距离为6，列方程求解得a=2，c=1，由此能求出椭圆的标准方程；（2）设P（x0，y0），则Q（﹣x0，﹣y0），又A（﹣2，0），求出直线AP的方程得到M点的坐标，再求出，同理可得，进一步求出•=4+，结合点P在椭圆C上，故，即可证得结论；（3）设P（x1，y1），Q（x2，y2），将直线AP的方程y=k1（x+2）与椭圆方程联立得：，即（3+4k12）x2+16k12x+16k12﹣12=0，求出P点的坐标，由k1•k2=﹣1即可求出Q点的坐标，然后分类讨论即可得结论．【解答】（1）解：由题意，且，解得a=2，c=1．∴b=．∴椭圆的标准方程为．（2）证明：设P（x0，y0），则Q（﹣x0，﹣y0），又A（﹣2，0），∴直线AP的方程为y=（x+2），得M（0，），∴=（2，）．同理可得N（0，），=（2，），∴•=4+．又点P在椭圆C上，故，即，∴•=4+=1（定值）；（3）证明：设P（x1，y1），Q（x2，y2），将直线AP的方程y=k1（x+2）与椭圆方程联立得：，即（3+4k12）x2+16k12x+16k12﹣12=0．∴﹣2+x1=，x1=，y1=，∴P（，）．∵k1•k2=﹣1，∴Q（，）．当时，点P和点Q的横坐标相同，直线PQ的方程为x=﹣，由此可见，如果直线PQ经过定点R，则点R的横坐标一定为﹣．当时，，直线PQ的方程为y﹣=（x﹣），令x=﹣得：=0．∴直线PQ过定点R（﹣，0）．20．已知函数f（x）=lnx．（1）方程f（x+a）=x有且只有一个实数解，求a的值；（2）若函数的极值点x1，x2（x1＜x2）恰好是函数h（x）=f（x）﹣cx2﹣bx的零点，求的最小值．【考点】利用导数研究函数的单调性；函数零点的判定定理；利用导数研究函数的极值．【分析】（1）设切点为（x0，y0），求出函数y=f（x+a）的导数，求得切线的斜率，解方程可得a=1；（2）求出g（x）和h（x）的导数，运用韦达定理和函数的零点的定义，化简整理，构造函数，运用导数判断单调性，即可得到所求最小值．【解答】解：（1）由题意得，函数y=f（x+a）=ln（x+a）与直线y=x相切，设切点为（x0，y0），，∴，∴x0+a=1又有x0=ln（x0+a）∴x0=0，a=1；（2），h（x）=lnx﹣cx2﹣bx由已知的两根为x1，x2，当时方程x2﹣mx+1=0的△＞0，则x1+x2=m，x1x2=1，又由x1，x2为h（x）=lnx﹣cx2﹣bx的零点可得，两式相减，可解得①而=（x1﹣x2）[代入①式可得y===，令（0＜t＜1），由x1+x2=m，x1x2=1可得，则，设函数，而，则y=G（t）在单调递减，所以，即的最小值为．[几何证明选讲]（共1小题，满分0分）21．如图，A、B、C、D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC=ED．（Ⅰ）证明：CD∥AB；（Ⅱ）延长CD到F，延长DC到G，使得EF=EG，证明：A、B、G、F四点共圆．【考点】圆內接多边形的性质与判定．【分析】（I）根据两条边相等，得到等腰三角形的两个底角相等，根据四点共圆，得到四边形的一个外角等于不相邻的一个内角，高考等量代换得到两个角相等，根据根据同位角相等两直线平行，得到结论．（II）根据第一问做出的边和角之间的关系，得到两个三角形全等，根据全等三角形的对应角相等，根据平行的性质定理，等量代换，得到四边形的一对对角相等，得到四点共圆．【解答】解：（I）因为EC=ED，所以∠EDC=∠ECD因为A，B，C，D四点在同一圆上，所以∠EDC=∠EBA故∠ECD=∠EBA，所以CD∥AB（Ⅱ）由（I）知，AE=BE，因为EF=EG，故∠EFD=∠EGC从而∠FED=∠GEC连接AF，BG，△EFA≌△EGB，故∠FAE=∠GBE又CD∥AB，∠FAB=∠GBA，所以∠AFG+∠GBA=180°故A，B．G，F四点共圆[矩阵与变换]（共1小题，满分0分）22．已知矩阵A=．（1）求A的逆矩阵A﹣1；（2）求矩阵A的特征值λ1、λ2和对应的一个特征向量、．【考点】逆变换与逆矩阵；特征值与特征向量的计算．【分析】（1）通过变换可得→，即得结论；（2）令其特征多项式f（λ）为0，即可求得特征值，再分别在f（λ）=0代入特征值即可求得分别对应的特征向量．【解答】解：（1）∵→→→，∴A﹣1=；（2）∵A=，∴f （λ）==λ2﹣5λ+6=（λ﹣2）（λ﹣3）=0，解得λ1=2，λ2=3，设=，=，∵=2，∴，即=，∵∵=3，∴，即=．五、[坐标系与参数方程选讲]（共1小题，满分0分） 23．已知在直角坐标系x0y 内，直线l 的参数方程为（t 为参数）．以Ox 为极轴建立极坐标系，圆C 的极坐标方程为．（1）写出直线l 的普通方程和圆C 的直角坐标方程；（2）判断直线l 和圆C 的位置关系． 【考点】参数方程化成普通方程． 【分析】（1）消去参数t 得到直线l 的直角坐标方程，再利用ρ2=x 2+y 2，ρcos θ=x ，ρsin θ=y ，将圆的极坐标方程化成圆的直角坐标方程；（2）利用圆心C 到直线l 的距离d 与半径r 进行比较，即可判定直线l 和⊙C 的位置关系．【解答】解：（1）消去参数t ，得直线l 的直角坐标方程为y=2x ﹣3；，即ρ=2（sin θ+cos θ），两边同乘以ρ得ρ2=2（ρsin θ+ρcos θ）， 消去参数θ，得⊙C 的直角坐标方程为：（x ﹣1）2+（y ﹣1）2=2（2）圆心C 到直线l 的距离，所以直线l 和⊙C 相交．[不等式选讲]（共1小题，满分0分）24．设x ，y ，z ∈R +，求证：．【考点】综合法与分析法(选修）．【分析】由基本不等式可得①，②，③，把①②③相加可得即可证得结论．【解答】证明：∵x，y，z∈R+，∴由基本不等式可得①，②，③．把①②③相加可得≥2x+2y+2z，∴成立．七、必考题（共2小题，满分0分）25．如图，四棱锥P﹣ABCD的底面为矩形，PA是四棱锥的高，PB与DC所成角为45°，F 是PB的中点，E是BC上的动点．（Ⅰ）证明：PE⊥AF；（Ⅱ）若BC=2BE=2AB，求直线AP与平面PDE所成角的大小．．【考点】用空间向量求直线与平面的夹角；向量语言表述线线的垂直、平行关系；用空间向量求直线间的夹角、距离．【分析】（Ⅰ）建立空间直角坐标系，求出各点的坐标，以及向量PE，AF的坐标，得到其数量积为0即可证明结论．（Ⅱ）先根据条件求出D的坐标以及，的坐标，进而求出平面PDE的法向量的坐标，再代入向量的夹角计算公式即可得到答案．【解答】解：（Ⅰ）建立如图所示空间直角坐标系．设AP=AB=2，BE=a则A（0，0，0），B（0，2，0），P（0，0，2），F（0，1，1），E（a，2，0）于是，，，则，所以AF⊥PE．…（Ⅱ）若，则，，=（2，2，﹣2），设平面PDE的法向量为=（x，y，z），由，得：，令x=1，则，于是，而设直线AP与平面PDE所成角为θ，则sinθ==．∴直线AP与平面PDE所成角为60°．26．已知抛物线C：y2=2px（p＞0）的焦点为F，直线y=4与y轴的交点为P，与C的交点为Q，且|QF|=|PQ|．（Ⅰ）求C的方程；（Ⅱ）过F的直线l与C相交于A、B两点，若AB的垂直平分线l′与C相交于M、N两点，且A、M、B、N四点在同一圆上，求l的方程．【考点】直线与圆锥曲线的综合问题．【分析】（Ⅰ）设点Q的坐标为（x0，4），把点Q的坐标代入抛物线C的方程，求得x0=，根据|QF|=|PQ|求得p的值，可得C的方程．（Ⅱ）设l的方程为x=my+1 （m≠0），代入抛物线方程化简，利用韦达定理、中点公式、弦长公式求得弦长|AB|．把直线l′的方程代入抛物线方程化简，利用韦达定理、弦长公式求得|MN|．由于MN垂直平分线段AB，故AMBN四点共圆等价于|AE|=|BE|=|MN|，由此求得m的值，可得直线l的方程．【解答】解：（Ⅰ）设点Q的坐标为（x0，4），把点Q的坐标代入抛物线C：y2=2px（p＞0），可得x0=，∵点P（0，4），∴|PQ|=．又|QF|=x0+=+，|QF|=|PQ|，∴+=×，求得p=2，或p=﹣2（舍去）．故C的方程为y2=4x．（Ⅱ）由题意可得，直线l和坐标轴不垂直，y2=4x的焦点F（1，0），设l的方程为x=my+1（m≠0），代入抛物线方程可得y2﹣4my﹣4=0，显然判别式△=16m2+16＞0，y1+y2=4m，y1•y2=﹣4．∴AB的中点坐标为D（2m2+1，2m），弦长|AB|=|y1﹣y2|==4（m2+1）．又直线l′的斜率为﹣m，∴直线l′的方程为x=﹣y+2m2+3．过F的直线l与C相交于A、B两点，若AB的垂直平分线l′与C相交于M、N两点，把线l′的方程代入抛物线方程可得y2+y﹣4（2m2+3）=0，∴y3+y4=，y3•y4=﹣4（2m2+3）．故线段MN的中点E的坐标为（+2m2+3，），∴|MN|=|y3﹣y4|=，∵MN垂直平分线段AB，故AMBN四点共圆等价于|AE|=|BE|=|MN|，∴+DE2=MN2，∴4（m2+1）2 ++=×，化简可得m2﹣1=0，∴m=±1，∴直线l的方程为x﹣y﹣1=0，或x+y﹣1=0．2016年10月25日。

江苏省泰州市姜堰区2020-2021学年高三下学期期初考试数学试卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知F 是双曲线22:4||C kx y k +=（k 为常数）的一个焦点，则点F 到双曲线C 的一条渐近线的距离为（ ） A ．2kB ．4kC ．4D ．22．在等差数列{}n a 中，若244,8a a ==，则7a =（ ） A ．8B ．12C ．14D ．103．为实现国民经济新“三步走”的发展战略目标，国家加大了扶贫攻坚的力度．某地区在2015 年以前的年均脱贫率（脱离贫困的户数占当年贫困户总数的比）为70%．2015年开始，全面实施“精准扶贫”政策后，扶贫效果明显提高，其中2019年度实施的扶贫项目，各项目参加户数占比（参加该项目户数占 2019 年贫困户总数的比）及该项目的脱贫率见下表：那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的（ ） A ．2728倍 B ．4735倍 C ．4835倍 D ．75倍 4．若函数2()x f x x e a =-恰有3个零点，则实数a 的取值范围是（ ） A ．24(,)e +∞ B ．24(0,)e C ．2(0,4)e D ．(0,)+∞5．若函数f(x)＝13x 3＋x 2－23在区间(a ，a ＋5)上存在最小值，则实数a 的取值范围是A ．[－5，0)B ．(－5，0)C ．[－3，0)D ．(－3，0)6．在ABC 中，角,,A B C 的对边分别为,,a b c ，若cos (2)cos c a B a b A -=-，则ABC 的形状为（ ）C．等腰或直角三角形D．钝角三角形7．已知半径为2的球内有一个内接圆柱，若圆柱的高为2，则球的体积与圆柱的体积的比为（）A．43B．916C．34D．1698．若实数,x y满足不等式组121210x yx yx y+≥-⎧⎪-≤-⎨⎪--≤⎩，则234x y-+的最大值为（）A．1-B．2-C．3 D．29．双曲线C：2215x ym-=（0m>），左焦点到渐近线的距离为2，则双曲线C的渐近线方程为（）A．250x y±=B．250x y±=C．520x y±=D．50x y±=10．已知复数z满足202020191z i i⋅=+（其中i为虚数单位），则复数z 的虚部是（）A．1-B．1 C．i-D．i11．已知某几何体的三视图如图所示，则该几何体外接球的表面积为（）A．24πB．28πC．32πD．36π12．P是正四面体ABCD的面ABC内一动点，E为棱AD中点，记DP与平面BCE成角为定值θ，若点P的轨迹为一段抛物线，则tanθ=（）A2B．2C2D．2二、填空题：本题共4小题，每小题5分，共20分。