高一数学课堂资料《必修二空间平行与垂直综合练习》

1.2.2空间中的平行关系(三)一、基础过关1．给出下列结论，正确的有()①平行于同一条直线的两个平面平行；②平行于同一平面的两个平面平行；③过平面外两点，不能作一个平面与已知平面平行；④若a，b为异面直线，则过a与b平行的平面只有一个．A．1个B．2个C．3个D．4个2．若正n边形的两条对角线分别与面α平行，则这个正n边形所在的平面一定平行于平面α，那么n的取值可能是() A．12 B．8 C．6 D．53．正方体EFGH—E1F1G1H1中，下列四对截面中，彼此平行的一对截面是()A．平面E1FG1与平面EGH1B．平面FHG1与平面F1H1GC．平面F1H1H与平面FHE1D．平面E1HG1与平面EH1G4．α、β是两个不重合的平面，a、b是两条不同的直线，在下列条件下，可判定α∥β的是() A．α，β都平行于直线a、bB．α内有三个不共线的点到β的距离相等C．a，b是α内两条直线，且a∥β，b∥βD．a、b是两条异面直线，且a∥α，b∥α，a∥β，b∥β5．过正方体ABCD－A1B1C1D1的三个顶点A1、C1、B的平面与底面ABCD所在平面的交线为l，则l与A1C1的位置关系是________．6．有下列几个命题：①平面α内有无数个点到平面β的距离相等，则α∥β；②α∩γ＝a，α∩β＝b，且a∥b(α，β，γ分别表示平面，a，b表示直线)，则γ∥β；③平面α内一个三角形三边分别平行于平面β内的一个三角形的三条边，则α∥β；④平面α内的一个平行四边形的两边与平面β内的一个平行四边形的两边对应平行，则α∥β.其中正确的有________．(填序号)7． 如图，在长方体ABCD —A 1B 1C 1D 1中，E 、F 、E 1、F 1分别是AB 、CD 、A 1B 1、C 1D 1的中点．求证：平面A 1EFD 1∥平面BCF 1E 1.8． 如图，在三棱柱ABC －A 1B 1C 1中，M 是A 1C 1的中点，平面AB 1M ∥平面BC 1N ，AC ∩平面BC 1N ＝N .求证：N 为AC 的中点．二、能力提升9． 如图所示，P 是三角形ABC 所在平面外一点，平面α∥平面ABC ，α分别交线段PA 、PB 、PC 于A ′、B ′、C ′，若PA ′∶AA ′＝2∶3，则S △A ′B ′C ′∶S △ABC 等于( ) A ．2∶25B ．4∶25C ．2∶5D ．4∶510．α，β，γ为三个不重合的平面，a ，b ，c 为三条不同的直线，则有下列命题，不正确的是( )① ⎭⎪⎬⎪⎫a ∥c b ∥c ⇒a ∥b; ② ⎭⎪⎬⎪⎫a ∥γb ∥γ⇒a ∥b ； ③ ⎭⎪⎬⎪⎫α∥c β∥c ⇒α∥β； ④ ⎭⎪⎬⎪⎫α∥γβ∥γ⇒α∥β； ⑤ ⎭⎪⎬⎪⎫α∥c a ∥c ⇒α∥a; ⑥ ⎭⎪⎬⎪⎫α∥γa ∥γ⇒a ∥α. A ．④⑥B ．②③⑥C ．②③⑤⑥D ．②③ 11．如图所示，在正方体ABCD —A 1B 1C 1D 1中，E 、F 、G 、H 分别是棱CC 1、C 1D 1、D 1D 、CD 的中点，N 是BC 的中点，点M 在四边形EFGH 及其内部运动，则M 满足________时，有MN ∥平面B 1BDD 1.12．如图，已知在正方体ABCD—A1B1C1D1中，M、E、F、N分别是A1B1、B1C1、C1D1、D1A1的中点．求证：(1)E、F、D、B四点共面；(2)平面AMN∥平面EFDB.三、探究与拓展13．如图所示，在底面是平行四边形的四棱锥P－ABCD中，点E 在PD上，且PE∶ED＝2∶1，在棱PC上是否存在一点F，使BF∥平面AEC？并证明你的结论．答案1．B 2.D 3.A 4.D5．平行6．③7．证明 ∵E 、E 1分别是AB 、A 1B 1的中点， ∴A 1E 1∥BE 且A 1E 1＝BE .∴四边形A 1EBE 1为平行四边形．∴A 1E ∥BE 1.∵A 1E ⊄平面BCF 1E 1，BE 1⊂平面BCF 1E 1.∴A 1E ∥平面BCF 1E 1.同理A 1D 1∥平面BCF 1E 1，A 1E ∩A 1D 1＝A 1，∴平面A 1EFD 1∥平面BCF 1E 1.8．证明 ∵平面AB 1M ∥平面BC 1N ，平面ACC 1A 1∩平面AB 1M ＝AM ，平面BC 1N ∩平面ACC 1A 1＝C 1N ，∴C 1N ∥AM ，又AC ∥A 1C 1，∴四边形ANC 1M 为平行四边形，∴AN ＝C 1M ＝12A 1C 1＝12AC ， ∴N 为AC 的中点．9．B 10．C11．M ∈线段FH12．证明 (1)∵E 、F 是B 1C 1、C 1D 1的中点，∴EF 綊12B 1D 1，∵DD1綊BB1，∴四边形D1B1BD是矩形，∴D1B1∥BD.∴EF∥BD，即EF、BD确定一个平面，故E、F、D、B四点共面．(2)∵M、N是A1B1、A1D1的中点，∴MN∥D1B1∥EF.又MN⊄平面EFDB，EF⊂平面EFDB.∴MN∥平面EFDB.连接NE，则NE綊A1B1綊AB.∴四边形NEBA是平行四边形．∴AN∥BE.又AN⊄平面EFDB，BE⊂平面EFDB.∴AN∥平面BEFD.∵AN、MN都在平面AMN内，且AN∩MN＝N，∴平面AMN∥平面EFDB.13．解当F是棱PC的中点时，BF∥平面AEC，证明如下：取PE的中点M，连接FM，则FM∥CE，①由EM＝12PE＝ED，知E是MD的中点，设BD∩AC＝O，则O为BD的中点，连接OE，则BM∥OE，②由①②可知，平面BFM∥平面AEC，又BF⊂平面BFM，∴BF∥平面AEC.。

1.2.2 空间中的平行关系(一)一、基础过关1． 经过平面α外的两个点作该平面的平行平面，可以作出( ) A ．0个B ．1个C ．0个或1个D ．1个或2个 2． 若∠AOB ＝∠A 1O 1B 1，且OA ∥O 1A 1，OA 与O 1A 1的方向相同，则下列结论中正确的是( )A ．OB ∥O 1B 1且方向相同B ．OB ∥O 1B 1C ．OB 与O 1B 1不平行D ．OB 与O 1B 1不一定平行3． 分别和两条异面直线平行的两条直线的位置关系是( )A ．一定平行B ．一定相交C ．一定异面D ．相交或异面 4． 正方体ABCD －A 1B 1C 1D 1中，P 、Q 分别为AA 1、CC 1的中点，则四边形D 1PBQ 是( )A ．正方形B ．菱形C ．矩形D ．空间四边形5． 空间两个角α、β，且α与β的两边对应平行且α＝60°，则β为________．6． 在正方体ABCD —A 1B 1C 1D 1中，判断下列直线的位置关系：(1)直线A 1B 与直线D 1C 的位置关系是________；(2)直线A 1B 与直线B 1C 的位置关系是________；(3)直线D 1D 与直线D 1C 的位置关系是________；(4)直线AB 与直线B 1C 的位置关系是________．7． 已知直线AB 、CD 是异面直线，求证：直线AC 、BD 是异面直线．8． 如图所示，四边形ABEF 和ABCD 都是直角梯形，∠BAD ＝∠FAB＝90°，BC 綊12AD ，BE 綊12FA ，G 、H 分别为FA 、FD 的中点． (1)证明：四边形BCHG 是平行四边形；(2)C 、D 、F 、E 四点是否共面？为什么？二、能力提升9． 如图所示，已知三棱锥A －BCD 中，M 、N 分别为AB 、CD 的中点，则下列结论正确的是( ) A ．MN ≥12(AC ＋BD ) B ．MN ≤12(AC ＋BD ) C ．MN ＝12(AC ＋BD ) D ．MN <12(AC ＋BD ) 10．在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别为棱AA 1，CC 1的中点，则在空间中与三条直线A 1D 1，EF ，CD 都相交的直线( ) A ．不存在B ．有且只有两条C ．有且只有三条D ．有无数条 11．一个正方体纸盒展开后如图所示，在原正方体纸盒中有如下结论：①AB ∥CM ；②EF 与MN 是异面直线；③MN ∥CD .以上结论中正确结论的序号为________．12．如图所示，P 是△ABC 所在平面外一点，D 、E 分别是△PAB 、△PBC的重心．求证：DE ∥AC ，DE ＝13AC . 三、探究与拓展13．如图所示，在三棱锥A —BCD 中，E ，F ，G 分别是棱AB ，AC ，AD 上的点，且满足AE AB ＝AF AC ＝AG AD. 求证：△EFG ∽△BCD .答案1．C 2.D 3.D 4．B5．60°或120°6．(1)平行 (2)异面 (3)相交 (4)异面7．证明 假设AC 和BD 不是异面直线，则AC 和BD 在同一平面内，设这个平面为α.∵AC ⊂α，BD ⊂α，∴A 、B 、C 、D 四点都在α内，∴AB ⊂α，CD ⊂α.这与已知中AB 和CD 是异面直线矛盾，故假设不成立．∴直线AC 和BD 是异面直线．8．(1)证明 由已知FG ＝GA ，FH ＝HD ，可得GH 綊12AD .又BC 綊12AD ， ∴GH 綊BC ，∴四边形BCHG 为平行四边形．(2)解 由BE 綊12AF ，G 为FA 中点知，BE 綊FG ， ∴四边形BEFG 为平行四边形，∴EF ∥BG .由(1)知BG 綊CH ，∴EF ∥CH ，∴EF 与CH 共面．又D ∈FH ，∴C 、D 、F 、E 四点共面．9．D10．D11.①②12．证明 连接PD 并延长交AB 于M ，连接PE 并延长交BC 于N ，则M 为AB 的中点，N 为BC 的中点，∴MN ∥AC ，又PD DM ＝PE EN ＝21， ∴DE ∥MN ，∴DE ∥AC .又DE MN ＝PD PM ＝23， ∴DE ＝23MN ，又∵MN ＝12AC ， ∴DE ＝13AC . 13．证明 在△ABC 中，∵AE AB ＝AF AC， ∴EF ∥BC 且EF BC ＝AE AB. 同理，EG ∥BD 且EG BD ＝AE AB. 又∵∠FEG 与∠CBD 的对应两边方向相同，∴∠FEG ＝∠CBD .∵EF BC ＝EG BD， ∴△EFG ∽△BCD .。

必修2 空间中的垂直关系基础知识点一、选择题：1.若斜线段AB是它在平面α上的射影的长的2倍，则AB与平面α所成的角是( ).A.60°B.45°C.30°D.120°2.直线l⊥平面α，直线m⊂α，则( ).A.l⊥mB.l∥mC.l，m异面D.l，m相交而不垂直3.如图所示，PO⊥平面ABC，BO⊥AC，在图中与AC垂直的线段有( ).A.1条B.2条C.3条D.4条4.若平面α⊥平面β，平面β⊥平面γ，则( ).A.α∥γB.α⊥γC.α与γ相交但不垂直D.以上都有可能5.已知长方体ABCDA1B1C1D1，在平面AB1上任取一点M，作ME⊥AB于E，则( ).A.ME⊥平面ACB.ME ⊂平面ACC.ME∥平面ACD.以上都有可能6.如图，设P是正方形ABCD外一点，且PA⊥平面ABCD，则平面PAB与平面PBC、平面PAD的位置关系是( ).A.平面PAB与平面PBC、平面PAD都垂直B.它们两两垂直C.平面PAB与平面PBC垂直，与平面PAD不垂直D.平面PAB与平面PBC、平面PAD都不垂直二、填空题：7.在正方体A1B1C1D1ABCD中，E，F分别是棱AB，BC的中点，O是底面ABCD的中心(如图)，则EF与平面BB1O的关系是________.8.若a，b表示直线，α表示平面，下列命题中正确的有________个.①a⊥α，b∥α⇒a⊥b; ②a⊥α，a⊥b⇒b∥α；③a∥α，a⊥b⇒b⊥α；④a⊥α，b⊥α⇒a∥b.9.α、β是两个不同的平面，m、n是平面α及β外的两条不同的直线，给出四个论断：①m⊥n；②α⊥β；③m⊥α；④n⊥β.以其中三个论断作为条件，余下的一个论断作为结论，写出你认为正确的一个命题________.10.如图，正方体ABCDA1B1C1D1中，截面C1D1AB与底面ABCD所成二面角C1ABC的大小为________.三、解答题：11.如图所示，在Rt △AOB 中，∠ABO=π6，斜边AB=4，Rt △AOC 可以通过Rt △AOB 以直线AO 为轴旋转得到，且二面角BAOC 是直二面角，D 是AB 的中点.求证：平面COD ⊥平面AOB.12.如图，在四棱锥P ­ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD=DC ，E 是PC 的中点，作EF ⊥PB 交PB 于点F.(1)求证：PA ∥平面EDB ；(2)求证：PB ⊥平面EFD.综合提高1.已知l ，m ，n 为两两垂直的三条异面直线，过l 作平面α与直线m 垂直，则直线n 与平面α的关系是( ).A.n ∥αB.n ∥α或n ⊂αC.n ⊂α或n 与α不平行D.n ⊂α2.已知平面α⊥平面β，α∩β=l ，点A ∈α，A ∉l ，直线AB ∥l ，直线AC ⊥l ，直线m ∥α，m ∥β，则下列四种位置关系中，不一定成立的是( ).A.AB ∥mB.AC ⊥mC.AB ∥βD.AC ⊥β3.一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，那么这两个二面角( ).A.相等B.互补C.相等或互补D.关系无法确定4.如图，正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，现在沿SE，SF，EF 把这个正方形折成一个四面体，使G1、G2、G3重合，重合后的点记为G.给出下列关系：①SG⊥平面EFG；②SE⊥平面EFG；③GF⊥SE；④EF⊥平面SEG.其中成立的有( ).A.①②B.①③C.②③D.③④5.如果三棱锥的三个侧面两两相互垂直，则顶点在底面的正投影是底面三角形的________心.6.已知三棱柱ABCA1B1C1的侧棱与底面边长都相等，若A1在底面ABC内的射影为△ABC的中心，则AB1与ABC底面所成的角的正弦值等于________.7.将正方形ABCD沿对角线BD折成直二面角ABDC，有如下四个结论：①AC⊥BD；②△ACD是等边三角形；③AB与平面BCD成60°的角；④AB与CD 所成的角为60°.其中真命题的编号是________(写出所有真命题的编号).8.如图，A、B、C、D为空间四点，在△ABC中，AB=2，AC=BC=2，等边三角形ADB以AB为轴运动，当平面ADB⊥平面ABC时，则CD=________.9.如图所示，四边形ABCD为正方形，SA垂直于四边形ABCD所在的平面，过点A且垂直于SC的平面分别交SB，SC，SD于点E，F，G.求证：AE⊥SB，AG⊥SD.10.如图，在四棱锥P－ABCD中，PO⊥面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=90°.(1)求证：PC⊥BC.(2)求点A到平面PBC的距离.11.如图，已知平面PAB⊥平面ABC，平面PAC⊥平面ABC，AE⊥平面PBC，E为垂足.(1)求证：PA⊥平面ABC；(2)当E为△PBC的垂心时，求证：△ABC是直角三角形.12.(创新拓展)已知△BCD 中，∠BCD=90°，BC=CD=1，AB ⊥平面BCD ，∠ADB=60°，E ，F 分别是AC ，AD 上的动点，且AE AC =AF AD=λ(0＜λ＜1). (1)求证：不论λ为何值，总有平面BEF ⊥平面ABC ；(2)当λ为何值时，平面BEF ⊥平面ACD?参考答案基础篇1.答案 A ；解析 斜线段、垂线段以及射影构成直角三角形.如图所示，∠ABO即是斜线AB 与平面α所成的角，又AB=2BO ，所以cos ∠ABO=OB AB =12.所以∠ABO=60°.故选A.2.答案 A ；解析 无论l 与m 是异面，还是相交，都有l ⊥m ，考查线面垂直的定义，故选A.3.答案 D ；解析 ∵PO ⊥平面ABC ，∴PO ⊥AC ，又∵AC ⊥BO ，∴AC ⊥平面PBD ， ∴平面PBD 中的4条线段PB ，PD ，PO ，BD 与AC 垂直.4.答案 D ；解析 以正方体为模型：相邻两侧面都与底面垂直；相对的两侧面都与底面垂直；一侧面和一对角面都与底面垂直，故选D.5.答案 A ；解析 由于ME ⊂平面AB 1，平面AB 1∩平面AC=AB ，且平面AB 1⊥平面AC ，ME ⊥AB ，则ME ⊥平面AC.6.答案A；解析∵PA⊥平面ABCD，∴PA⊥BC.又BC⊥AB，PA∩AB=A，∴BC⊥平面PAB，∵BC⊂平面PBC，∴平面PBC⊥平面PAB.由AD⊥PA，AD⊥AB，PA∩AB=A，得AD⊥平面PAB.∵AD⊂平面PAD，∴平面PAD ⊥平面PAB.由已知易得平面PBC与平面PAD不垂直，故选A.7.答案垂直；解析由正方体性质知AC⊥BD，BB1⊥AC，∵E，F是棱AB，BC 的中点，∴EF∥AC，∴EF⊥BD，EF⊥BB1，∴EF⊥平面BB1O.8.答案2；解析由线面垂直的性质定理知①④正确.9.答案①③④⇒②或②③④⇒①；解析如图，PA⊥α，PB⊥β，垂足分别为A、B，α∩β=l，l∩平面PAB=O，连接OA、OB，可证明∠AOB为二面角αlβ的平面角，则∠AOB=90°⇔PA⊥PB.10.答案45°；解析∵AB⊥BC，AB⊥BC1，∴∠C1BC为二面角C1ABC的平面角，大小为45°.11.证明：由题意：CO⊥AO，BO⊥AO，∴∠BOC是二面角BAOC的平面角，又∵二面角BAOC是直二面角，∴CO⊥BO，又∵AO∩BO=O，∴CO⊥平面AOB，∵CO⊂平面COD，∴平面COD⊥平面AOB.12.证明：(1)连接AC，AC交BD于点O.连接EO，如图.∵底面ABCD是正方形，∴点O是AC的中点.在△PAC中，EO是中位线，∴PA∥EO.而EO⊂平面EDB且PA⊄平面EDB.所以PA∥平面EDB.(2)∵PD⊥底面ABCD且DC⊂底面ABCD.∴PD⊥DC.∵PD=DC，可知△PDC是等腰直角三角形，而DE是斜边PC的中线，∴DE⊥PC.①同样由PD⊥底面ABCD，得PD⊥BC.∵底面ABCD是正方形，有DC⊥BC，∴BC⊥平面PDC.而DE⊂平面PDC，∴BC⊥DE.②由①和②推得DE⊥平面PBC.而PB⊂平面PBC，∴DE⊥PB.又EF⊥PB且DE∩EF=E，∴PB⊥平面EFD.综合提高1.答案A；解析∵l⊂α，且l与n异面，∴n⊄α，又∵m⊥α，n⊥m，∴n ∥α.2.答案D；解析如图，AB∥l∥m，AC⊥l，m∥l⇒AC⊥m，AB∥l⇒AB∥β.故选D.3.答案D；解析如图所示，平面EFDG⊥平面ABC，当平面HDG绕DG转动时，平面HDG始终与平面BCD垂直，所以两个二面角的大小关系不确定，因为二面角HDGF 的大小不确定.4.答案B；解析由SG⊥GE，SG⊥GF，得SG⊥平面EFG，排除C、D；若SE⊥平面EFG，则SG∥SE，这与SG∩SE=S矛盾，排除A，故选B.5.答案垂；解析三棱锥的三个侧面两两相互垂直，则三条交线两两互相垂直，可证投影是底面三角形的垂心.6.答案：23；解析由题意知，三棱锥A1ABC为正四面体(各棱长都相等的三棱锥)，设棱长为a ，则AB 1=3a ，棱柱的高A 1O=63a(即点B 1到底面ABC 的距离)，故AB 1与底面ABC 所成的角的正弦值为A 1O AB 1=23.' 7.答案 ①②④；解析 本题主要考查了空间直线与直线、直线与平面的夹角.8.答案 2；解析 取AB 的中点E ，连接DE ，CE ，因为△ADB 是等边三角形，所以DE ⊥AB.当平面ADB ⊥平面ABC 时，因为平面ADB ∩平面ABC=AB ，所以DE ⊥平面ABC.又CE ⊂平面ABC 可知DE ⊥CE. 由已知可得DE=3，EC=1，在Rt △DEC 中，CD=DE 2＋CE 2=2.9.证明 因为SA ⊥平面ABCD ，所以SA ⊥BC.又BC ⊥AB ，SA ∩AB=A ，所以BC ⊥平面SAB ，又AE ⊂平面SAB ，所以BC ⊥AE.因为SC ⊥平面AEFG ，所以SC ⊥AE.又BC ∩SC=C ，所以AE ⊥平面SBC ，所以AE ⊥SB.同理可证AG ⊥SD.10.(1)证明 因为PD ⊥平面ABCD ，BC ⊂平面ABCD ，所以PD ⊥BC.因为∠BCD=90°，所以BC ⊥CD.又PD ∩CD=D ，所以BC ⊥平面PCD.而PC ⊂平面PCD ，所以PC ⊥BC.(2)解 如图，过点A 作BC 的平行线交CD 的延长线于E ，过点E 作PC 的垂线，垂足为F ，则有AE ∥平面PBC ，所以点A 到平面PBC 的距离等于点E 到平面PBC 的距离.又EF ⊥PC ，BC ⊥平面PCD ，则EF ⊥BC.BC ∩PC=C ，所以EF ⊥平面PBC.EF 即为E 到平面PBC 的距离.又因为AE ∥BC ，AB ∥CD ，所以四边形ABCE 为平行四边形.所以CE=AB=2. 又PD=CD=1，PD ⊥平面ABCD ，CD ⊂平面ABCD.所以PD ⊥CD ，∠PCD=45°. 所以EF= 2.即点A 到平面PBC 的距离为 2.11.证明 (1)在平面ABC 内取一点D ，作DF ⊥AC 于F ，∵平面PAC ⊥平面ABC ，且交线为AC ，∴DF ⊥平面PAC.又∵PA ⊂平面PAC ，∴DF ⊥PA.作DG ⊥AB 于G ，同理可证DG ⊥PA.∵DG ∩DF=D ，∴PA ⊥平面ABC.(2)连接BE 并延长交PC 于H.∵E 是△PBC 的垂心，∴PC ⊥BH ，又AE ⊥平面PBC ，故AE ⊥PC ，且AE ∩BE=E ，∴PC ⊥平面ABE.∴PC ⊥AB.又∵PA ⊥平面ABC ，∴PA ⊥AB ，且PA ∩PC=P ，∴AB ⊥平面PAC ，∴AB ⊥AC ，即△ABC 是直角三角形. 12.(1)证明 ∵AB ⊥平面BCD ，∴AB ⊥CD.∵CD ⊥BC 且AB ∩BC=B ，∴CD ⊥平面ABC.又∵AE AC =AF AD=λ(0＜λ＜1)，∴不论λ为何值，恒有EF ∥CD ，∴EF ⊥平面ABC. 又EF ⊂平面BEF ，∴不论λ为何值恒有平面BEF ⊥平面ABC.(2)解 由(1)知，EF ⊥BE ，又平面BEF ⊥平面ACD ，∴BE ⊥平面ACD ，∴BE ⊥AC. ∵BC=CD=1，∠BCD=90°，∠ADB=60°，AB ⊥平面BCD ，∴BD=2，AB=2tan 60°= 6.AC=AB 2＋BC 2=7， 由AB 2=AE ·AC 得AE=67，∴λ=AE AC =67，故当λ=67时，平面BEF ⊥平面ACD.。

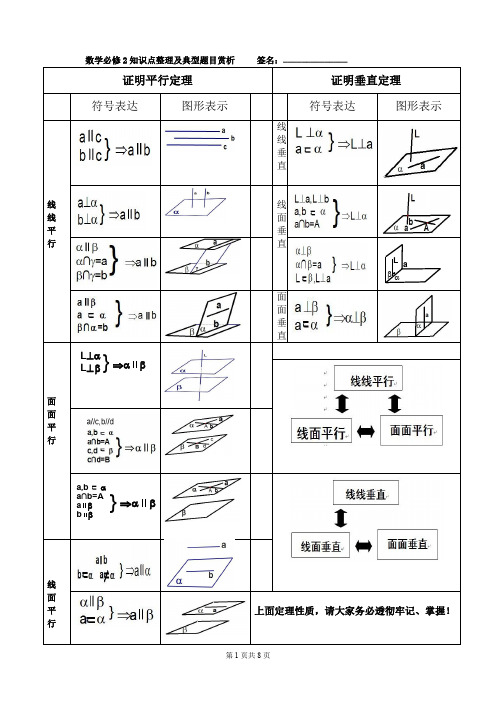
——————————————线 线垂直线面垂直面面垂直上面定理性质，请大家务必透彻牢记、掌握！ a,b αa∩b=A β其他重要基础知识：1. 直线与直线的位置关系：相交、平行、异面2. 直线与平面的位置关系：平行、相交、直线在平面内3. 平面与平面的位置关系：平行、相交4.*************************************【经典练习】************************************空间平行问题训练1、空间四边形ABCD ，E 、F 、G 、H 分别为各边中点，求证： EH //平面BCD ，BD //平面EFGH2、空间四边形ABCD ，E 、F 、G 、H 分别为各边上的点，且EH //FG ，求证：EH //BD3、正方体D C B A ABCD ''''-中，E 为1DD 中点， 求证：//1BD 平面AEC4 如图，ABCD 是平行四边形，S 是平面ABCD 外一点，M 为SC 的中点. 求证：SA ∥平面MDB.5、已知正方体ABCD –A 1B 1C 1D 1 证：平面AB 1D 1∥平面C 1BD .6、 直三棱柱111C B A ABC 中，AC=BC ，点D 是AB 求证：//1BC 平面D CA 17.棱锥P －ABCD 的底面ABCD 为平行四边形，M 、N 分别为ＡＢ，ＣＰ的中点。

求证： ＭＮ／／平面ＰＡＤ8、如图所示，在正方体ABCD —A 1B 1C 1D 1MN ∥平面AA 1B 1B .9、棱锥P －ABCD 的底面是一直角梯形，AB ∥CD ，BA ⊥AD ，CD ＝2AB ，P A ⊥底面ABCD ，E 为PC 的中点，求证：BE // 平面P AD10.直棱柱111C B A ABC -中，AB=AC=5，61==BC BB ，D 、E 分别是1AA 和C B 1的中点 （1)求证：DE//平面ABC （2）求三棱锥E-BCD 的体积学习反思：挑战数学系列-----直线、平面垂直的判定及其性质**************************班级：_________ 签名：__________*******************问题1、直线与平面垂直的判定定理。

．平行与垂直综合问题．已知直线，和平面α，β满足⊥，⊥α，α⊥β，则()．⊥β．∥β或⊂β．⊥α．∥α或⊂α解析：在平面β内作直线垂直于α，β的交线，则由α⊥β得直线⊥α.又⊥α，所以∥.若⊂β，结合图形知，要满足题中限制条件，显然只能∥α或⊂α；同理⊄β，仍有∥α或⊂α.综上所述，正确．．若三个平面α，β，γ，之间有α∥γ，β⊥γ，则α与β()．垂直．平行．相交．以上三种可能都有．对于任意的直线与平面α相交，在平面α内不可能有直线，使与()．平行．相交．垂直．互为异面直线．给出以下四个命题，其中真命题有①②④(填序号)．①如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行；②如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面；③如果两条直线都平行于一个平面，那么这两条直线互相平行；④如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．．已知平面α外不共线的三点，，，且∥α，则正确的结论是() ．平面必平行于α．平面必与α相交．平面必不垂直于α．存在△的一条中位线平行于α或在α内．设直线⊂平面α，过平面α外一点且与，α都成°角的直线有且只有() ．条．条．条．条解析：如图所示与α成°角的直线一定是以为顶点的圆锥的母线所在直线，当∠＝∠＝°时，直线，都满足条件，故选..下列命题中，正确的是()．经过不同的三点有且只有一个平面．分别在两个平面内的两条直线一定是异面直线．垂直于同一个平面的两条直线是平行直线．垂直于同一个平面的两个平面平行．用α表示一个平面，表示一条直线，则平面α内至少有一条直线与()．平行．相交．异面．垂直．若，表示直线，α表示平面，则下列命题中，正确的个数为()。

人教版高一数学必修2空间直线的垂直关系练习题（含答案详解）必修 2 空间中的垂直关系基础知识点一、选择题：1. 若斜线段 AB 是它在平面α上的射影的长的 2倍，则 AB 与平面α所成的角是( ).2. 直线l ⊥平面α，直线m? α，则 ( ).A.l ⊥mB.l ∥mC.l ，m 异面D.l ， m 相交而不垂直3. 如图所示，PO ⊥平面 ABC ，BO ⊥AC ，在图中与 AC 垂直的线段有 ( ). 4. 若平面α⊥平面β，平面β⊥平面γ，则( ). C.30 °D.120C.3条 D.4 条A. α∥γ B. α⊥γ C. α与γ相交但不垂直D.以上都有可能5. 已知长方体 ABCD 1AB 1C 1D 1，在平面 AB 1上任取一点 M ，作ME ⊥AB 于 E ，则( ).A.ME ⊥平面 ACB.ME ? 平面 ACC.ME ∥平面 ACD. 以上都有A.1 条B.2可能6. 如图，设P是正方形ABCD外一点，且PA⊥平面ABCD，则平面PAB与平面PBC、平面PAD的位置关系是( ).A. 平面PAB与平面PBC、平面PAD都垂直B. 它们两两垂直C. 平面PAB与平面PBC垂直，与平面PAD不垂直D. 平面PAB与平面PBC、平面PAD都不垂直二、填空题：7. _________________________________ 在正方体A1B1C1D1ABCD 中，E，F分别是棱AB，BC的中点，O是底面ABCD的中心（如图），则EF与平面BB1O 的关系是 ______________________________ .8. 若a， b 表示直线，α表示平面，下列命题中正确的有___ 个.①a⊥α，b∥α? a⊥b; ②a⊥α，a⊥b? b∥α；③a∥α，a⊥b? b⊥α；④a⊥α，b⊥α? a∥b.9. α、β是两个不同的平面，m、n 是平面α及β外的两条不同的直线，给出四个论断：① m⊥n；②α⊥β；③m⊥α；④n⊥β. 以其中三个论断作为条件，余下的一个论断作为结论，写出你认为正确的一个命题 __ .10. 如图，正方体ABCD1AB1C1D1中，截面C1D1AB与底面ABCD所成二面角C1ABC的三、解答题：π11. 如图所示，在Rt△AOB中，∠ABO=6 ，斜边AB=4，Rt △AOC可以通过Rt △AOB 以直线AO为轴旋转得到，且二面角BAOC 是直二面角，D是AB的中点.求证：平面COD⊥平面AOB.12. 如图，在四棱锥P - ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=D，C E 是PC的中点，作EF⊥PB交PB于点F.(1) 求证：PA∥平面EDB；(2) 求证：PB⊥平面EFD.综合提高1. 已知l ，m，n 为两两垂直的三条异面直线，过l 作平面α与直线m垂直，则直线n 与平面α的关系是( ).A.n ∥αB.n ∥α或n? αC.n ? α或n 与α不平行D.n ? α2. 已知平面α⊥平面β，α∩β =l，点A∈α，A?l ，直线AB∥l ，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是( ).A.AB∥mB.AC ⊥mC.AB ∥βD.AC ⊥β3. 一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，那么这两个二面角( ).A. 相等B. 互补C. 相等或互补D. 关系无法确定4. 如图，正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，现在沿SE，SF，EF 把这个正方形折成一个四面体，使G1、G2、G3 重合，重合后的点记为G.给出下列关系：①SG⊥平面EFG；②SE⊥平面EFG；③GF⊥ SE；④EF⊥平面SEG. 其中成立的有( ).A. ①②B. ①③C. ②③D. ③④5. 如果三棱锥的三个侧面两两相互垂直，则顶点在底面的正投影是底面三角形的心.6. 已知三棱柱ABCA1B1C1的侧棱与底面边长都相等，若A1在底面ABC内的射影为△ABC的中心，则AB1 与ABC底面所成的角的正弦值等于.7. 将正方形ABCD沿对角线BD折成直二面角ABDC，有如下四个结论：①AC⊥BD；②△ ACD是等边三角形；③ AB与平面BCD成60°的角；④ AB与CD 所成的角为60°.其中真命题的编号是 _____ ( 写出所有真命题的编号).8. 如图，A、B、C、D为空间四点，在△ ABC中，AB=2，AC=BC= 2，等边三角形ADB以AB为轴运动，当平面ADB⊥平面ABC时，则CD= .9. 如图所示，四边形ABCD为正方形，SA垂直于四边形ABCD 所在的平面，过点 A 且垂直于SC的平面分别交SB，SC，SD于点E，F，G.求证：AE⊥SB，AG⊥SD.10. 如图，在四棱锥P－ABCD中，PO⊥面ABCD，PD=DC=BC，=1AB=2，AB∥DC，∠ BCD=9°0 .(1) 求证：PC⊥BC.(2) 求点A到平面PBC的距离.11. 如图，已知平面PAB⊥平面ABC，平面PAC⊥平面ABC，AE⊥平面PBC，E 为垂足.(1) 求证：PA⊥平面ABC；(2) 当 E 为△ PBC的垂心时，求证：△ ABC是直角三角形.12. （创新拓展）已知△ BCD中，∠BCD=9°0 ，BC=CD=，1AB⊥平面BCD，∠ADB=60°，AE AFE，F 分别是AC，AD上的动点，且A AE C=A A F D=λ(0 <λ<1).(1) 求证：不论λ为何值，总有平面BEF⊥平面ABC；(2) 当λ为何值时，平面BEF⊥平面ACD?参考答案基础篇1. 答案A；解析斜线段、垂线段以及射影构成直角三角形. 如图所示，∠ABO OB1即是斜线AB与平面α所成的角，又AB=2BO，所以cos∠ABO=AB=2. 所以∠ ABO=60°. 故选 A.2. 答案A；解析无论l 与m是异面，还是相交，都有l ⊥m，考查线面垂直的定义，故选 A.3. 答案D；解析∵PO⊥平面ABC，∴ PO⊥AC，又∵ AC⊥BO，∴ AC⊥平面PBD，∴平面PBD中的4条线段PB，PD，PO，BD与AC垂直.4. 答案D；解析以正方体为模型：相邻两侧面都与底面垂直；相对的两侧面都与底面垂直；一侧面和一对角面都与底面垂直，故选 D.5. 答案A；解析由于ME? 平面AB1，平面AB1∩平面AC=AB，且平面AB1⊥平面AC，ME⊥AB，则ME⊥平面AC.6. 答案A；解析∵PA⊥平面ABCD，∴ PA⊥BC.又BC⊥AB，PA∩AB=A，∴BC⊥平面PAB，∵ BC? 平面PBC，∴平面PBC⊥平面PAB. 由AD⊥PA，AD⊥AB，PA∩AB=A，得AD⊥平面PAB.∵AD?。

数学·必修2(人教A版)2.3直线、平面垂直的判定及其性质2.3.3直线与平面垂直、平面与平面垂直的性质基础达标1．若直线a与平面α不垂直，那么在平面α内与直线a垂直的直线()A．只有一条B．有无数条C．是平面α内的所有直线D．不存在解析：找到a在平面α内的射影，在平面α内有无数条直线与射影垂直，也与a垂直．答案：B2.如图，PA⊥平面ABCD，且四边形ABCD为矩形，下列结论中不正确的是()A．PB⊥BCB．PD⊥CDC．PO⊥BDD．PA⊥BD答案：C3．圆O的半径为4，PO垂直圆O所在的平面，且PO＝3，那么点P到圆上各点的距离是________．答案：54．平面α⊥平面β，直线a∥α，则a与β的位置关系为__________．答案：a∥β或a⊂β或a与β相交5．设a，b，c表示三条直线，α，β表示两个平面，下列命题中不正确的是()A. ⎭⎪⎬⎪⎫a ⊥αα∥β⇒a ⊥βB.⎭⎪⎬⎪⎫a ⊥αb ⊥βα⊥β⇒a ⊥b C. ⎭⎪⎬⎪⎫b ∥c b ⊂αc ⊄α⇒c ∥α D.⎭⎪⎬⎪⎫a ∥αb ⊥a ⇒b ⊥α答案：D巩固提升6．关于直线m ，n 与平面α，β，有以下四个命题：①若m ∥α，n ∥β且α∥β，则m ∥n ②若m ⊥α，n ⊥β且α⊥β，则m ⊥n ③m ⊥α，n ∥β且α∥β，则m ⊥n ④m ∥α，n ⊥β且α⊥β，则m ∥n其中真命题的序号是( )A ．①②B ．③④C ．①④D ．②③答案：D7．已知，△ABC 所在平面外一点V ，VB ⊥平面ABC ，平面VAB ⊥平面VAC .求证：AC ⊥BA .证明：过B作BD⊥VA于D，∵平面VAB⊥平面VAC，∴BD⊥平面VAC，∴BD⊥AC，又∵VB⊥平面ABC，∴VB⊥AC，又∵BD∩VB＝B，∴AC⊥平面VBA，∴AC⊥BA.8．如下图(左)所示，在边长为1的等边三角形ABC中，D，E 分别是AB，AC边上的点，AD＝AE，F是BC的中点，AF与DE 交于点G，将△ABF沿AF折起，得到如下图(右)所示的三棱锥ABCF，其中BC＝2 2.(1)证明：DE∥平面BCF；解析：在等边三角形ABC中，AD＝AE，∴ADDB ＝AEEC，在折叠后的三棱锥ABCF中也成立，∴DE∥BC.又∵DE⊄平面BCF，BC⊂平面BCF，∴DE∥平面BCF.(2)证明CF⊥平面ABF.解析：在等边三角形ABC中，F是BC的中点，所以AF⊥BC，即AF⊥CF，①且BF＝CF＝12.∵在三棱锥ABCF中，BC＝2 2，∴BC2＝BF2＋CF2.∴CF⊥BF.②∵BF∩AF＝F，∴CF⊥平面ABF.(3)当AD＝32时，求三棱锥FDEG的体积V F－DEG.解析：由(1)可知，GE∥CF，结合(2)可得GE⊥平面DFG.∴V FDEG＝V EDFG＝13×12×DG×FG×GE＝13×12×13×⎝⎛⎭⎪⎫13×32×13＝3 324.。

2020-2021学年高一下学期空间的垂直问题精编1、三棱柱ABC− A1B1C1中，侧棱AA1 ⊥底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC中点，则下列叙述正确的是（）．A. CC1与B1E是异面直线B. AC⊥平面ABB1A1C. AE，B1C1为异面直线，且AE⊥ B1C1D. A1C1//平面AB1E2、如图，△ ABC是等腰直角三角形，其中∠A = 90°，且DB⊥ BC，∠BCD = 30°，现将△ABC折起，使得二面角A−BC−D的平面角为直角，则下列叙述正确的是() ①→→；BD⋅ AC = 0②平面BCD的法向量与平面ACD的法向量垂直③异面直线BC与AD所成的角为60°；④直线DC与平面ABC所成的角为30°．A. ①③B. ①④C. ①③④D. ①②③④3、对于任意的直线l与平面α，在平面α内必有直线m，使m与l（）．A. 平行B. 相交C. 垂直D. 互为异面直线4、三棱锥V− ABC中，侧面VBC⊥底面ABC，∠ABC = 45°，VA = VB，AC = AB，则（）．A. AC⊥BCB. VB⊥ACC. VA⊥BCD. VC⊥AB5、如图，在正四面体P− ABC中，D、E、F分别是棱AB、BC、CA的中点，下面四个结论中不成立的是（）．A. BC//平面PDFB. DF⊥平面PAEC. 平面PDF⊥平面ABCD. 平面PAE⊥平面ABC6、已知AB⊥平面ACD，DE⊥平面ACD，△ ACD为等边三角形，边长为2a，AD = DE = 2AB，F 为CD的中点．(1) 求证：AF//平面BCE；(2) 求证：平面BCE⊥平面CDE．7、下列五个正方体图形中，l是正方体的一条体对角线，点M、N、P分别为其所在棱的中点，能得出l⊥平面MNP的图形的序号是．（写出所有符合要求的图形序号）．8、在正四面体P− ABC中，D，E，F分别是边AB，BC，CA的中点，则下列四个结论中不成立的是（）．A. BC//平面PDFB. DF⊥平面PAEC. 平面PDF⊥平面ABCD. 平面PAE⊥平面ABC9、如图，AB是⊙ O的直径，C是圆周上不同于A，B的任意一点，PA⊥平面ABC，则四面体P−ABC的四个面中，直角三角形的个数是()A. 4个B. 3个C. 2个D. 1个10、如图，D为圆锥的顶点，O是圆锥底面的圆心，AE为底面直径，AE = AD．△ ABC是底面圆的内接正三角形，P为DO上一点，PO =√6 DO．6证明：PA⊥平面PBC．11、如图，在三棱柱ABC− A1B1C1中，CC1 ⊥平面ABC，D，E，F，G分别为AA1，AC，A1C1，BB1的中点，AB = BC = √5，AC = AA1 = 2．求证：AC⊥平面BEF．12、如图，在底面是菱形的四棱锥P− ABCD中，∠ABC = 60°，PA = AC = a，PB = PD = √2a，点E在PD上，且PE: ED = 2: 1．(1) 证明：PA⊥平面ABCD．(2)在棱PB上是否存在一点F，使三棱锥F− ABC是正三棱锥？证明你的结论．13、如图，在正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，D是EF的中点，现在沿SE，SF及EF把这个正方形折成一个四面体，使G1，G2，G3三点重合，重合后的点记为G，那么在四面体S− EFG中，必有（）．A. SD⊥△ EFG所在平面B. SG⊥△ EFG所在平面C. GD⊥△ SEF所在平面D. GF⊥△ SEF所在平面14、如图，在梯形ABCD中，AB//CD，AD = DC = CB = 1，∠BCD = 120°，四边形BFED为矩形，平面BFED⊥平面ABCD，BF = 1．求证：AD⊥平面BFED．15、设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：①若m⊥ α，n//α，则m⊥ n②若α//β，β//γ，m⊥ α，则m⊥ γ③若m//α，n//α，则m//n④若α⊥ γ，β⊥ γ，则α//β其中正确命题的序号是()A. ①和②B. ②和③C. ③和④D. ①和④16、如图，四棱柱ABCD− A1B1C1D1的底面ABCD是平行四边形，AC⊥ CB，侧面B1BCC1 ⊥底面ABCD，E, F分别是AB, C1D的中点．(1) 求证：EF//平面B1BCC1．(2) 求证：EF⊥ AC．(3) 在线段EF上是否存在点G，使得AC⊥平面C1D1G？并说明理由．17、如图，在三棱柱ABC− A1B1C1中，AC = BC = AB1 = 2，AB1 ⊥平面ABC，AC1 ⊥ AC，D，E分别是AC，B1C1的中点．(1) 证明：AC⊥ B1C1．(2) 证明：DE//平面AA1B1B．18、在如图所示的几何体中，四边形ABCD是正方形，MA⊥平面ABCD，PD//MA，E，G，F分别为MB，PB，PC的中点，且AD = PD = 2MA．(1) 求证：平面EFG⊥平面PDC．(2) 求三棱锥P− MAB与四棱锥P− ABCD的体积之比．19、已知平面α与平面β相交，直线m⊥ α，则()A.β内必存在直线与m平行，且存在直线与m垂直B.β内不一定存在直线与m平行，也不一定存在直线与m垂直C.β内不一定存在直线与m平行，但必存在直线与m垂直D.β内必存在直线与m平行，但不一定存在直线与m垂直20、如图，在四棱锥P− ABCD中，PD⊥平面ABCD，底面ABCD为矩形，PD = DC = 4，AD = 2，E为PC的中点．(1) 求证：DE⊥平面PBC．(2) 求三棱锥P− ADE的体积．(3)在线段AC上是否存在一点M，使得PA//平面EDM，若存在，求出AM的长．若不存在，请说明理由．（本题不能使用空间向量解题）21、如图所示，在四棱锥S− ABCD中，AB//CD，BC⊥ CD，侧面SAB为等边三角形．AB = BC = 2，CD = SD = 1．(1) 证明：SD⊥平面SAB．(2) 求AB与平面SBC所成角的正弦值．22、如图所示，正方形ABCD和四边形ACEF所在的平面互相垂直．EF//AC，AB = √2，CE = EF = 1．(1) 求证：AF//平面BDE．(2) 求证：CF⊥平面BDE．23、在三棱柱ABC− A1B1C1中，AB⊥ AC，B1C⊥平面ABC，E，F分别是AC，B1C的中点．(1) 求证：EF//平面AB1C1．(2) 求证：平面AB1C⊥平面ABB1．24、如图，在正方体ABCD− A1B1C1D1中，M为棱DD1的中点，O为线段AC的中点．(1) 证明：直线BD1//平面MAC．(2)求异面直线AM和BD1所成角的余弦值．(3)证明：B1O⊥ AC．（本题不能使用空间向量解题）25、如图，在四棱锥P− ABCD中，底面ABCD为等腰梯形，BC//AD且BC = 2AD = 4，PA = PD = AB = √5，E为PB的中点，O为AD的中点．(1) 求证：AE//平面PCD．(2) 若平面PAD⊥平面ABCD，求证：BO⊥ PC．26、三棱柱ABC− A1B1C1被平面A1B1C截去一部分后得到如图所示几何体，BB1 ⊥平面ABC，∠ABC = 90°，BC = BB1，E为棱B1C上的动点(不包含端点)，平面ABE交A1C于点F．(1) 求证：EF//AB．(2) 若点E为B1C中点，求证：平面ABE⊥平面A1B1C．27、如图，四棱锥P− ABCD的底面为平行四边形，点E、F分别在CD、BC上，G为PA中点，且PE⊥平面ABCD．(1) 若PF⊥ BC，求证：平面PBC⊥平面PEF；(2) 求证：PC//平面BDG．28、如图，D为圆锥的顶点，O是圆锥底面的圆心，△ ABC是底面的内接正三角形，P为DO上一点，∠APC = 90°．(1) 证明：平面PAB⊥平面PAC．(2) 设DO = √2，圆锥的侧面积为√3π，求三棱锥P− ABC的体积．29、如图，在直角梯形ABCD中，AD//BC，∠BAD = π，AB = BC = 1 AD = a，E是AD的中点，2 2O是AC与BE的交点．将△ ABE沿BE折起到如图2中△ A1BE的位置，得到四棱锥A1 −BCDE．(1) 证明：CD⊥平面A1OC．(2) 当平面A1BE⊥平面BCDE时，四棱锥A1 −BCDE的体积为36√2，求a的值．30、如图，四棱锥P− ABCD中，AP⊥平面PCD，AD//BC，AB = BC = 1 AD，E，F分别为线段2AD，PC的中点．(1) 求证：AP//平面BEF．(2) 求证：BE⊥平面PAC．2021 春季第8 讲空间的垂直问题姣姐精编题解析1、C【解析】A 选项: CC1 与B1E都在平面CC1B1B内，故不是异面直线，A错误；B 选项: 若AC⊥ 平面ABB1A1 ，又AB⊂平面ABB1A1，∴AC⊥ AB，由题干知三角形A1B1C1 是正三角形，∴AC与AB成60°矛盾，B 错误；C 选项: 由题图可知AE，B1C1 为异面直线，∵E是BC中点，三角形ABC为正三角形，∴AE⊥ BC，又BC//B1C1 ，∴AE⊥ B1C1 ，C正确；D 选项: 若A1C1//平面AB1E，∵AC//A1C1 ，∴AC// 平面AB1E，而AC与平面AB1E相交，矛盾，D 错误．2、B→→【解析】∵平面ABC∩平面BCD = BC，BD⊥ BC，∴ BD⊥平面ABC，∴ BD⊥ AC，∴BD⋅ AC = 0，故①正确；∵平面BCD⊥平面ABC，∴平面BCD与平面ACD不垂直，∴平面BCD的法向量与平面ACD的法向量不垂直，故②错误；分别取AB、AC、BD中点E、F、G，连接EF、EG、FG、BF．∵ EF//BC，EG//AD，∴ ∠FEG或其补角为直线BC与AD所成的角．设BD = 2，则BC =2√3，AB = AC = √6，∴ EF = √3．∴ AD = √10，∴ EG = √10．∵直角三角形BFG中，∠GBF =25 1790°，BG = 1，BF = √30，∴ FG =√34，∴ cos ∠FEG3+2−2 = −√30 ∴BC与AD所2 2 23×√10，异面直线10√2成的角为arccos √30，故③错误；∵ BD⊥平面ABC，∴ ∠BCD为直线DC与平面ABC所成的角，∴直10线DC与平面ABC所成的角为30°，故④正确．综上，选B．3、C【解析】对于任意的直线l与平面α，分两种情况：（1）若直线l⊂ α，则l与m是共面直线，则存在直线m⊥ l或m//l；（2）l不在平面α内，且l⊥ α，则平面α内任意一条直线都垂直于l；若l与α不垂直，则它的射影在平面α内为一条直线，在平面α内必存在直线m垂直于它的射影，则m与l垂直；若l//α，则存在直线m⊥ l．综上所述，对于任意的直线l和平面α，在平面α内必有直线m，使m与l垂直．故选C．4、C【解析】A 选项: ∵∠ABC = 45∘，AC = AB，∴∠ACB = ∠ABC = 45∘．故A错误．B 选项: 若VB⊥ AC，又AC⊂平面ABC，VB⊂平面VBC，平面VBC⊥ 平面ABC，则AC⊥ 平面VBC，与∠ACB = 45∘矛盾，故B错误．C 选项: 取BC边中点D，连接AD，VD．∵VA = VB，AC = AB．∴AD⊥ BC，VD⊥BC．又AD⊂平面ADV，VD⊂平面ADV，AD∩ VD= D，∴BC⊥ 平面ADV，又VA⊂平面ADV，∴VA⊥ BC．故C正确．D 选项: 若VC⊥ AB，又VC⊂平面VBC，AB⊂平面ABC，平面VBC⊥平面ABC．则AB⊥ 平面VBC，与∠ABC = 45∘矛盾，故D错误．5、C【解析】正四面体P− ABC中，D、F分别为边AB、AC的中点，显然DF//BC，所以BC//平面PDF；假设P点在底面的射影为点O，则OP⊥ AE，而AE⊥ BC，所以DF⊥平面PAE；因为OP⊥平面ABC，而OP与平面PDE相交，故平面PDF与平面ABC不垂直；O点在直线AE上，则平面PAE⊥平面ABC．6、【解析】(1) 如图，取CE中点G，连接FG，BG．因为AB⊥平面ACD，DE⊥平面ACD，所以AB//DE．1又因为F为CD中点，所以GF//DE，且GF =1DE，2即有GF//AB．因为AB =DE，所以GF = AB．2所以四边形GFAB为平行四边形，AF//BG．又AF⊄平面BCE，BG⊂平面BCE，所以AF//平面BCE．(2) ∵△ ACD为正三角形，∴AF⊥ CD．∵DE⊥平面ACD又AF⊂平面ACD，∴DE⊥ AF．又AF⊥ CD，CD∩ DE = D，∴AF⊥平面CDE．又BG//AF，∴BG⊥平面CDE．又∵BG⊂平面BCE，∴平面BCE⊥平面CDE．7 、①④⑤【解析】设定正方体的顶点如图，连接DB，AC，∵ M，N分别为AD、CD中点，∴ MN//AC，∵四边形ABCD为正方形，∴ AC⊥ BD，∵ BB′⊥平面ABCD，AC⊂平面ABCD，∴ BB′⊥ AC，∵ BB′∩ DB = B，BB′⊂平面DBB′，BD⊂平面DBB′，∴ AC⊥平面DBB′，∵ DB′⊂平面DBB′，∴ AC⊥ DB′，∵ MN//AC，∴ DB′⊥ MN，同理可证DB′⊥ MP，DB′⊥ NF，∵ MP∩ NP = P，MF⊂平面MNP，NF⊂平面MNP，∴ DB′⊥平面MNP，即l垂直于平面MNP，故①正确，④中由①中证明可知l⊥ MP，∵ MN//AC，AC⊥ l，∴ l⊥ MN，∴ l⊥平面MNP，同理可证明⑤中l⊥平面MNP．8、C【解析】A选项，如图所示，因为点D，F分别为线段AB，AC的中点，所以有DF//BC，且BC⊄平面PDF，所以BC//平面PDF，所以A项不符合题意；B选项，如图所示，因为P− ABC是正四面体，所以△ ABC，△ PBC为正三角形，且点E为BC中点，故AE⊥ BC，PE⊥ BC，又由A选项得知DF//BC，所以DF⊥ AE，DF⊥ PE，且PE∩ AE = E，所以DF⊥平面PAE，所以B项不合题意；C选项，如图所示，过点P作底面ABC的垂线，根据正四面体的性质，可知垂足G为△ ABC的重心，即PG⊥平面ABC，根据三角形重心的性质，可知G点不在DF上，所以直线PG与平面PDF相交于P点，所以平面PDF与平面ABC不垂直，所以选项C符合题意；D选项，如图所示，由C项和正三角形的性质可知点G在线段AE上，且PG⊥平面ABC．而PG⊂平面PAE，PG⊄平面ABC，所以平面PAE⊥平面ABC，所以D项不合题意．9、A【解析】∵ AB是圆O的直径，∴ ∠ACB = 90°，即BC⊥ AC，三角形ABC是直角三角形，又∵PA⊥圆O所在的平面，∴△ PAC，△ PAB是直角三角形．且BC在这个平面内，∴ PA⊥ BC，因此BC垂直于平面PAC中两条相交直线，∴ BC⊥平面PAC，∴△ PBC是直角三角形. 从而△ PAB，△PAC，△ ABC，△ PBC是直角三角形，∴在四面体P− ABC中直角三角形的个数是4．故选：A．10、【解析】设DO = a，由题设可得PO = √6 a，AO = √3 a，AB = a，PA = PB = PC = √2 a，6 3 2因此PA2 + PB2 = AB2，从而PA⊥ PB，又PA2 + PC2 = AC2，故PA⊥ PC，所以PA⊥平面PBC．11、【解析】∵AB = BC，且E是AC的中点，∴AC⊥ BE，∵在三棱柱ABC− A1B1C1中，E，F分别是AC，A1C1的中点，∴EF//CC1∵CC1 ⊥平面ABC，∴EF⊥平面ABC，∵AC⊂平面ABC，∴EF⊥ AC，∵EF，BE⊂平面BEF，EF∩ BE = E，∴AC⊥平面BEF．12、【解析】(1) ∵底面ABCD是菱形，∠ABC = 60°，∴AB = AD = AC = a．在△ PAB中，由PA = AB = a，知PA2 + AB2 = 2a2 = PB2，则PA⊥AB．同理PA⊥ AD．又AB∩ AD = A，∴PA⊥平面ABCD．(2) 在棱PB上不存在点F，使三棱锥F− ABC是正三棱锥．事实上，假设在棱PB上存在点F，使三棱锥F− ABC是正三棱锥．过F作底面ABC的垂线，垂直为O，则O为△ ABC的中心，在平面PAB内，过F作FM//PA，交AB于M，则FM⊥平面PAB，这样，过平面ABC外一点F，有两条直线FO，FM与平面ABC垂直，错误．故假设不成立，即在棱PB上不存在点F，使三棱锥F− ABC是正三棱锥．13 、B【解析】∵在折叠过程中，始终有SG1 ⊥ G1E，SG3 ⊥ G3F，即SG⊥ GE，SG⊥ GF，∴SG⊥平面EFG．故选B．14、【解析】在梯形ABCD中，∵AB//CD，AD = DC = CB = 1，∠BCD = 120°，∴AB = 2．∴BD2 = AB2 + AD2− 2AB⋅ AD⋅ cos 60°= 3，∴AB2 = AD2 + BD2，∴AD⊥ BD．∵平面BFED⊥平面ABCD，平面BFED∩平面ABCD = BD，DE⊂平面BFED，DE⊥ DB，∴DE⊥平面ABCD，∴DE⊥ AD，又DE∩ BD = D，∴AD⊥平面BFED．15、A【解析】对于①，因为n//α，所以经过n作平面β，使β∩ α = l，可得n//l，又因为m⊥ α，l⊂ α，所以m⊥ l，结合n//l得m⊥ n．由此可得①是真命题；对于②，因为α//β且β//γ，所以α//γ，结合m⊥ α，可得m⊥ γ，故②是真命题；对于③，设直线m、n是位于正方体上底面所在平面内的相交直线，而平面α是正方体下底面所在的平面，则有m//α且n//α成立，但不能推出m//n，故③不正确；对于④，设平面α、β、γ是位于正方体经过同一个顶点的三个面，则有α⊥ γ且β⊥ γ，但是α⊥ β，推不出α//β，故④不正确．综上所述，其中正确命题的序号是①和②故选：A．16、【解析】(1) 方法一：取CC1中点M，连接FM，BM．在△ CC1D中，因为F, M分别为C1D, C1C中点，1所以FM//CD，FM =CD．2在平行四边形ABCD中，因为CD//AB，E为AB中点，所以FM//EB，FM = EB．所以四边形FMBE是平行四边形．所以EF//BM．又因为BM⊂平面B1BCC1，EF⊄平面B1BCC1，所以EF//平面B1BCC1．方法二：取CD的中点M，连接FM，EM．在△ CC1D中因为F, M分别为C1D, CD的中点，所以FM//CC1．在平行四边形ABCD中，E, M分别为AB, CD的中点，所以EM//CB．又因为EM∩ FM = M，EM, FM⊂平面EFM，CC1 ∩ CB = C，CC1, CB⊂平面B1BCC1，所以平面EFM//平面B1BCC1．又因为EF⊂平面EFM，所以EF//平面B1BCC1．1(2) 因为平面B 1BCC 1 ⊥平面ABCD ，平面B 1BCC 1 ∩平面ABCD = BC ，AC ⊥ BC ，AC ⊂平面ABCD ，所以AC ⊥平面B 1BCC 1．由(1)知EF //平面B 1BCC 1，EF ⊄平面B 1BCC 1，所以EF ⊥ AC ．(3) 在线段EF 上不存在点G 使得AC ⊥平面C 1D 1G ． 假设存在点G 使得AC ⊥平面C 1D 1G ，因为C 1D 1 ⊂平面C 1D 1G ，所以AC ⊥ C 1D 1．而AC 与C 1D 1不垂直，矛盾．所以在线段EF 上不存在点G 使得AC ⊥平面C 1D 1G ．17 、【解析】 (1) 因为AB 1 ⊥平面ABC ，AC ⊂平面ABC ，所以AB 1 ⊥ AC ．因为AC 1 ⊥ AC ，AB 1 ∩ AC 1 = A ，AB 1，AC 1 ⊂平面AB 1C 1，所以AC ⊥平面AB 1C 1．因为B 1C 1 ⊂平面AB 1C 1，所以AC ⊥ B 1C 1．(2) 取A 1B 1的中点M ，连接MA 、ME ．因为E 、M 分别是B 1C 1、A 1B 1的中点， 所以ME //A 1C 1，且ME = 2 A 1C 1．1 在三棱柱ABC − A 1B 1C 1中，AD //A 1C 1，且AD =2 A 1C 1，所以ME //AD ，且ME = AD ，所以四边形ADEM 是平行四边形，所以DE //AM ．又AM ⊂平面AA 1B 1B ，DE ⊄平面AA 1B 1B ，所以DE //平面AA 1B 1B ．18 、【解析】 (1) 因为MA ⊥平面ABCD ，PD //MA ，所以PD ⊥平面ABCD ．又BC ⊂平面ABCD ，所以PD ⊥ BC ．因为四边形ABCD 为正方形，所以BC ⊥DC ． 又PD ∩ DC = D ，因此BC ⊥平面PDC在△ PBC 中，因为G ，F 分别为PB ，PC 的中点，所以GF //BC ，因此GF ⊥平面PDC ． 又GF ⊂平面EFG ，所以平面EFG ⊥平面PDC ．(2) 因为PD ⊥平面ABCD ，四边形ABCD 为正方形，不妨设MA = 1，则PD = AD = 2， V 1 8 所以 P−ABCD = 3 S 正方形ABCD ⋅ PD = 3．由于DA ⊥平面MAB ，且PD //MA ，所以DA 即为点P 到平面MAB 的距离， V 1 所 以 P−MAB = 3 S △MAB ⋅ DA = 1 × 3 1 × 1 × 2 × 2 = 2．2 3 所以V P−MAB : V P−ABCD = 1: 4．19 、 C【解析】 若β内存在直线n 与m 平行，由m ⊥ α知n ⊥ α，从而α ⊥ β，但α与β相交却不一定垂直， 矛盾．又设α ∩ β = a ，由m ⊥ α知m ⊥ a ，从而β内必有直线与m 垂直．20 、【解析】 (1) PD ⊥平面ABCD ，∴PD ⊥ BC ，∵ABCD 是矩形，∴BC ⊥ CD ，∵PD ∩ CD = D ，∴BC ⊥平面PDC ，∴BC ⊥ DE ．又∵PD = DC ，E 为PC 中点，∴DE ⊥ PC ，∵BC ∩ PC = C ，∴DE ⊥平面PBC ． (2) V = V 1 1 1 1 1 1 1 8． P−ADE E−PAD = 2 V C−PAD = 2 V P−DAC = 2 × 3 ⋅ S △DAC ⋅ |PD | = 2 × 2 × 4 × 2 × 4 × 3 = 3(3) 存在，当M 为AC 中点时，PA //面EDM ， 此时AM = 1 AC = 2 1 √42 2+ 22 = √5． 证明：∵E 、M 分别是PC 、AC 中点，∴EM //PA ，∵PA ⊄面EDM ，EM ⊂面EDM ，∴PA //面EDM ．21 、【解析】 (1) 证明：如图所示，取AB 的中点E ，连接DE ，则四边形BCDE 为矩形，DE = CB = 2．连接SE ，则SE ⊥ AB ，SE = √3．又SD = 1，故ED 2 = SE 2 + SD 2，所以∠DSE 为直角．由AB ⊥ DE ，AB ⊥ SE ，DE ∩ SE = E ，得AB ⊥平面SDE ，所以AB ⊥SD ． 又AB ∩ SE = E ，所以SD ⊥平面SAB ．(2) 因为AB⊥平面SDE，且AB⊂平面ABCD，所以平面ABCD⊥平面SDE，作SF⊥ DE ，垂足为F，则SF⊥平面ABCD，SF = SD×SE= √3，DE2作FG⊥ BC，垂足为G，则FG = DC =1．连接SG，则SG⊥ BC，又FG⊥ BC，SG∩ FG = G，故BC⊥平面SFG，平面SBC⊥平面SFG，作FH⊥ SG，H为垂足，则FH⊥平面SBC．于是FH = SF×FG= √3 = √21，即F到平面SBC的距离d为√21，SG√7 7 7因为ED//BC，所以ED//平面SBC，E到平面SBC的距离d也为√21．设AB与平面SBC所成的角为α，则sin α = dEB7 =√21．722、【解析】(1) 证明：如图所示，设AC与BD交于点G．1因为EF//AG，且EF = 1，AG =AC = 1，所以四边形AGEF为平行四边形，因此AF//EG．2因为EG⊂平面BDE，AF⊄平面BDE，所以AF//平面BDE．(2) 证明：如图，连接FG．因为EF//CG，EF = CG = 1，且CE = 1，所以平行四边形CEFG为菱形，因此CF⊥ EG．因为四边形ABCD为正方形，所以BD⊥ AC．又因为平面ACEF⊥平面ABCD，且平面ACEF∩平面ABCD = AC，所以BD⊥平面ACEF．因此CF⊥ BD．又BD∩ EG = G，所以CF⊥平面BDE．23、【解析】(1) 证明：因为E，F分别是AC，B1C的中点．所以EF//AB1，因为EF⊄平面AB1C1，AB1 ⊂平面AB1C1，所以EF//平面AB1C1．(2) 证明：因为B1C⊥平面ABC，AB⊂平面ABC，所以B1C⊥ AB，又因为AB⊥ AC，AC∩ B1C = C，AC⊂平面AB1C，B1C⊂平面AB1C，所以AB⊥平面AB1C，因为AB⊂平面ABB1，所以平面AB1C⊥平面ABB1．24、【解析】(1) 连接MO，∵M，O分别为DD1，DB中点，∴MO//D1B，∵MO⊂平面MAC，D1B⊄平面MAC，∴BD1//平面MAC．(2) 取CC1中点为Q，连接BQ，则AM//BQ，∴∠D1BQ即为AM与BD1所成的角，设正方体棱长为2a，则：D1B = 2√3a，BQ = √5a，D1Q = √5a，cos ∠D BQ = |12a2+5a2−5a2| = √15．1 2⋅2√3a⋅√5a5(3) 设正方体棱长为2a，则B O = √B B2 + BO2 = √(2a)2 + (√2a)2 = √6a，1 1OC = √2a，B1O2 + OC2 = B1C2，∴B1O⊥ AC．25、【解析】(1) 证明：如下图，取PC的中点F，连接EF，DF，∵ E为PB的中点，∴ EF//BC，EF =∵ AD//BC，AD =1 BC，21 BC，2∴ EF//AD，EF = AD，∴四边形AEFD为平行四边形，∴ AE//DF，又AE⊄平面PCD，DF⊂平面PCD，∴ AE//平面PCD．(2) 证明：连接OP，OC，∵ PA = PD，O为AD的中点，∴ PO⊥ AD，∵平面PAD⊥平面ABCD，∴ PO⊥平面ABCD，∴ PO⊥ OB.在等腰梯形ABCD中，利用BC = 2AD = 4，AB = √5，可求得OB = OC = 2√2，∴ OB2 + OC2 = BC2，∴ OB⊥ OC，∴ OB⊥平面POC，∴ BO⊥ PC．26、【解析】(1) 在三棱柱ABC− A1B1C1中，AA1//BB1，AA1 = BB1，∴四边形ABB1A1是平行四边形，∴ AB//A1B1，∵ AB⊄平面A1B1C，A1B1 ⊂平面A1B1C，∴ AB//平面A1B1C，又AB⊂平面ABEF，平面ABEF∩平面A1B1C = EF，∴ EF//AB．(2) ∵ BB1 ⊥平面ABC，AB⊂平面ABC，∴ BB1 ⊥ AB，∵ ∠ABC = 90°即AB⊥ BC，BC∩ BB1 = B，BC，BB1 ⊂平面BB1C，∴ AB⊥平面BB1C，又BE⊂平面BB1C，∴ AB⊥ BE，由(1)知AB//A1B1，∴ BE⊥ A1B1，∵ BC = BB1，点E为B1C的中点，∴ BE⊥ B1C，B1C∩ A1B1 = B1，B1C，A1B1 ⊂平面A1B1C，∴ BE⊥平面A1B1C，∵ BE⊂平面ABE．∴平面ABE⊥平面A1B1C．27、【解析】(1) 因为PE⊥平面ABCD，BC⊂平面ABCD，所以PE⊥ BC，又PF⊥ BC，PE∩ PF = P，PE⊂平面PEF，PF⊂平面PEF，所以BC⊥平面PEF．又BC⊂平面PBC，所以平面PBC⊥平面PEF．(2) 连接AC交BD于O，连接OG，因为四边形ABCD为平行四边形，所以OA = OC，又G为PA中点，所以OG//PC，又OG⊂平面BDG，PC⊄平面BDG，所以PC//平面BDG．28、【解析】(1) 证明：由题设可知，PA = PB = PC．由于△ ABC是正三角形，故可得△ PAC≅△ PAB，△ PAC≅△ PBC．又∠APC = 90°，故∠APB = 90°，∠BPC = 90°．从而PB⊥ PA，PB⊥ PC，故PB⊥平面PAC，所以平面PAB⊥平面PAC．(2) 设圆锥的底面半径为r，母线长为l．由题设可得rl = √3，l2− r2 = 2．解得r = 1，l =√3．从而AB= √3．由(1)可得PA2 + PB2 = AB2，故PA = PB = PC =√6．2所以三棱锥P− ABC的体积为1 × 1 3 2⋅PA⋅ PB⋅ PC = 1 × 13 23× (√6)2=√6．829、【解析】 (1) 在图1中， 1 因为AB = BC = ∠BAD = π， 2 所以BE ⊥ AC ， AD = a ，E 是AD 的中点，2即在图2中，BE ⊥ A 1O ，BE ⊥ OC ，从而BE ⊥面A 1OC ，由CD //BE ，所以CD ⊥面A 1OC ．(2) 因为平面A 1BE ⊥平面BCDE ，OA 1 ⊥ BE ，所以OA 1 ⊥平面BCDE ，即A 1O 是四棱锥A 1 − BCDE 的高， 根据图1得出A O = √ 2 AB = √2 a ， 1 2 2∴平行四边形BCDE 的面积S = BC ⋅ AB = a 2，1 12 √2 √2 3，V = 3 × S × A 1O = 3 × a × a = a 2 6 由√2 a 3 = 36√2，得出a = 6． 630 、【解析】 (1) 证明：如图，连接CE ， 1 ∵ AD //BC ，BC = AD ，E 为线段AD 的中点， 2∴四边形ABCE 是平行四边形，四边形BCDE 是平行四边形，设AC ∩ BE = O ，连接OF ，则O 是AC 的中点，∵ F 为线段PC 的中点，∴ PA //OF ，∵ PA ⊄平面BEF ，OF ⊂平面BEF ，∴ AP //平面BEF ． (2) ∵四边形BCDE 是平行四边形，∴ BE //CD ，∵ AP ⊥平面PCD ，CD ⊂平面PCD ，∴ AP ⊥ CD ，∴ BE ⊥ AP ，∵ AB = BC ，四边形ABCE 是平行四边形，∴四边形ABCE 是菱形，∴ BE ⊥ AC ，∵ AP ∩ AC = A ，∴ BE ⊥平面PAC ．高中数学各知识点公式定理记忆口诀大全《集合与函数》内容子交并补集，还有幂指对函数。

1.2.3空间中的垂直关系(二)一、基础过关1．已知三条相交于一点的线段PA、PB、PC两两垂直，点P在平面ABC外，PH⊥面ABC 于H，则垂足H是△ABC的() A．外心B．内心C．垂心D．重心2．设有直线m、n和平面α、β，则下列结论中正确的是()①若m∥n，n⊥β，m⊂α，则α⊥β；②若m⊥n，α∩β＝m，n⊂α，则α⊥β；③若m⊥α，n⊥β，m⊥n，则α⊥β.A．①②B．①③C．②③D．①②③3．过两点与一个已知平面垂直的平面() A．有且只有一个B．有无数个C．一个或无数个D．可能不存在4．平面α∩平面β＝l，平面γ⊥α，γ⊥β，则() A．l∥γB．l⊂γC．l与γ斜交D．l⊥γ5．若α⊥β，α∩β＝l，点P∈α，PD/∈l，则下列命题中正确的为________．(只填序号)①过P垂直于l的平面垂直于β；②过P垂直于l的直线垂直于β；③过P垂直于α的直线平行于β；④过P垂直于β的直线在α内．6．α、β、γ是两两垂直的三个平面，它们交于点O，空间一点P到α、β、γ的距离分别是2 cm、3 cm、6 cm，则点P到O的距离为________．7．如图，在三棱锥P－ABC中，PA⊥平面ABC，平面PAB⊥平面PBC.求证：BC⊥AB.8．如图，在直三棱柱ABC—A1B1C1中，E、F分别是A1B、A1C的中点，点D在B1C1上，A1D⊥B1C1.求证：(1)EF∥平面ABC；(2)平面A1FD⊥平面BB1C1C1.二、能力提升9．若平面α与平面β不垂直，那么平面α内能与平面β垂直的直线有() A．0条B．1条C．2条D．无数条10．设l是直线，α，β是两个不同的平面，下列结论中正确的是() A．若l∥α，l∥β，则α∥βB．若l∥α，l⊥β，则α⊥βC．若α⊥β，l⊥α，则l⊥βD．若α⊥β，l∥α，则l⊥β11．如图，在斜三棱柱ABC－A1B1C1中，∠BAC＝90°，BC1⊥AC，则点C1在底面ABC上的射影H必在直线__________上．12．如图所示，在多面体P—ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知BD＝2AD＝8，AB＝2DC＝4 5.(1)设M是PC上的一点，求证：平面MBD⊥平面PAD；(2)求四棱锥P—ABCD的体积．三、探究与拓展13．在直三棱柱ABC—A1B1C1的底面△ABC中，AB＝BC，能否在侧棱BB1上找到一点E，使得截面A1EC⊥侧面AA1C1C？若能找到，指出点E的位置；若不能找到，说明理由．答案1．C 2.B 3.C 4.D5．①③④6．7 cm7．证明在平面PAB内，作AD⊥PB于D.∵平面PAB⊥平面PBC，且平面PAB∩平面PBC＝PB.∴AD⊥平面PBC.又BC⊂平面PBC，∴AD⊥BC.又∵PA⊥平面ABC，BC⊂平面ABC，∴PA⊥BC，∴BC⊥平面PAB.又AB⊂平面PAB，∴BC⊥AB.8．证明(1)由E、F分别是A1B、A1C的中点知EF∥BC.因为EF⊄平面ABC，BC⊂平面ABC.所以EF∥平面ABC.(2)由三棱柱ABC—A1B1C1为直三棱柱知CC1⊥平面A1B1C1.又A1D⊂平面A1B1C1，故CC1⊥A1D.又因为A1D⊥B1C1，CC1∩B1C1＝C1，故A1D⊥平面BB1C1C，又A1D⊂平面A1FD，所以平面A1FD⊥平面BB1C1C.9．A10．B11．AB12．(1)证明在△ABD中，∵AD＝4，BD＝8，AB＝45，∴AD2＋BD2＝AB2.∴AD⊥BD.又∵面PAD ⊥面ABCD ，面PAD ∩面ABCD ＝AD ，BD ⊂面ABCD ，∴BD ⊥面PAD ，又BD ⊂面BDM ，∴面MBD ⊥面PAD .(2)解 过P 作PO ⊥AD ，∵面PAD ⊥面ABCD ，∴PO ⊥面ABCD ，即PO 为四棱锥P —ABCD 的高．又△PAD 是边长为4的等边三角形，∴PO ＝2 3. 在底面四边形ABCD 中，AB ∥DC ，AB ＝2DC ，∴四边形ABCD 为梯形．在Rt △ADB 中，斜边AB 边上的高为4×845＝855，此即为梯形的高． ∴S 四边形ABCD ＝25＋452×855＝24. ∴V P —ABCD ＝13×24×23＝16 3. 13．解 假设能找到符合题意的点E .如图所示，作EM ⊥A 1C 于点M .因为截面A 1EC ⊥侧面AA 1C 1C ，所以EM ⊥侧面AA 1C 1C .取AC 的中点N ， 连接MN ，BN ，因为AB ＝BC ，所以BN ⊥AC .又因为AA 1⊥BN ，所以BN ⊥侧面AA 1C 1C ，所以BN ∥EM .因为平面BEMN ∩平面AA 1C 1C ＝MN ，BE ∥平面AA 1C 1C ，所以BE ∥MN ∥A 1A .因为AN ＝NC ，所以A 1M ＝MC .因为四边形BEMN为矩形，所以BE＝MN＝12A1A.所以当E为BB1的中点时，平面A1EC⊥侧面AA1C1C.。