2013高教社杯全国大学生数学建模竞赛题目C题 古塔的变形
- 格式:doc
- 大小:24.50 KB
- 文档页数:1

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):5339所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2013 年 09 月 16 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):古塔的变形数学模型摘要:本文是研究关于古塔变形类型以及变形分析的模型,用Matlab画出古塔的三维结构可以看出它是近似于正八边形的形状。
因此,问题一我们用每层各个测量点坐标的平均值作为塔每层的中心坐标,再用中心坐标的三个坐标值分别对时间t做回归来得到确定古塔各层中心位置的通用方法。

古塔变形问题中弯曲情况的数学分析方法本文针对2013年全国大学生数学建模竞赛中古塔的变形中的弯曲问题,应用曲率的知识,分析其挠度,给出了弯曲变形情况的数学分析方法。
标签:古塔变形;曲率;挠度;拟合一、相关问题某古塔已有上千年历史,是我国重点保护文物。
管理部门委托测绘公司先后于1986年7月、1996年8月、2009年3月和2011年3月对该塔进行了4次观测。
根据提供的观测数据,分析该塔的弯曲变形情况。
二、古塔的弯曲情况的分析1.预备知识。
梁轴线上某点在梁变形后沿竖直方向的位移(横向位移)称为该点的挠度。
可以把古塔看成一个建筑上的梁,同样是相同的立体图形其中梁平面弯曲时其变形特点是:梁轴线既不伸长也不缩短,其轴线在纵向对称面内弯曲成一条平面曲线,我们可以把古塔的中心线看做一个梁的一个面的投影求解。
2.问题的解决方法。
对一般的观测经验可知,首先在建筑物的周围建立一个局部坐标系,根据墙面积的大小来确定观察点的个数,用无反光棱镜全站仪进行坐标的观测。
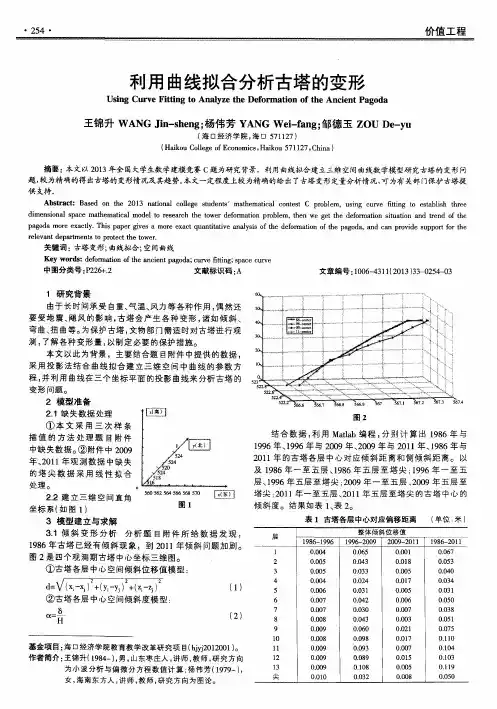
对该古塔的弯曲,主要从各层中心点考虑整体趋势,利用中心的坐标可以画出古塔中心线主视图、俯视图、侧视图。
观察对古塔中心线可以看出:(1)主視图只显示的是中心的扭曲情况,如果主视图显示的一条直线,则可以认为该古塔没有发生扭曲,否则发生了扭曲。
即古塔的外形发生扭曲变形。
(2)侧视图和主视图只显示了在xoz,yoz 的关系程度,如果该图显示的是一条垂直的直线,则没发生倾斜和弯曲,否则可以认为该中心线发生了倾斜和弯曲。
即古塔发生弯曲和倾斜。
首先任意选取一个平面来分析画古塔的是否弯曲,可以选取平面,用拟合和曲率来刻画古塔的弯曲建立模型为:选取二次函数为拟合函数,求出的各监测时间的函数为:由模型可以求出各年各点曲率变化函数:根据各年的各古塔曲率函数和各古塔的中心点,就可以得到各中心点的曲率值,进而算出弯曲程度。
参考文献[1]王有良.高层建筑倾斜变形数据处理.测绘学,33-2:3,2008[2]《建筑物沉降观测方法》DGJ32/J18-2006[3]《建筑变形测量规范》JGJ8-2007。

全国大学生数学建模竞
赛历年赛题
Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT
全国大学生数学建模竞赛历年赛题
2009:AB
CD
2010:A储油罐的变位识别与罐容表标定
B2010年上海世博会影响力的定量评估
C输油管的布置
D对学生宿舍设计方案的评价
2011:A城市表层土壤重金属污染分析
B交巡警服务平台的设置与调度
C企业退休职工养老金制度的改革
D天然肠衣搭配问题
2012:A葡萄酒的评价
B太阳能小屋的设计
C脑卒中发病环境因素分析及干预
D机器人避障问题
2013:A车道被占用对城市道路通行能力的影响
B碎纸片的拼接复原
C古塔的变形
D公共自行车服务系统
2014:A嫦娥三号软着陆轨道设计与控制策略B创意平板折叠桌
C生猪养殖场的经营管理
D储药柜的设计
2015:A太阳影子定位
B“互联网+”时代的出租车资源配置
C月上柳梢头
D众筹筑屋规划方案设计。

2013高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C 我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员 (打印并签名) :1.2.3.指导教师或指导教师组负责人 (打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):2013高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):古塔的变形摘要:本文研究的古塔的变形问题,通过对问题背景及附件资料进行深入地分析,采用数据拟合、求平均值等方法整理出具有科学性的分析数据。
通过对建筑物位移监测数据处理方法的研究, 采用自回归模型对位移监测数据进行处理, 根据建立的模型对具体建筑物的监测点的位移变化量进行预报。
经过计算分析, 根据位移量之间变化的关系而建立的自回归预测模型具备较高的拟合及预测精度,运用三维坐标系和数学软件将古塔的模型以空间模型的形式表现出来,直观且科学,对于研究古塔的变形具有较高的科学性和说服性。
再通过三维坐标之间的回归和三维坐标与时间的回归而分析出古塔的倾斜,弯曲,扭曲等变形状况,通过数学软件的计算及列表列图的方法将结果直观体现,通过大量的计算与分析,运用几何和代数方法将古塔的变形量以数学的方式说明。

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载).我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外地任何人(包括指导教师)研究、讨论与赛题有关地问题.我们知道,抄袭别人地成果是违反竞赛章程和参赛规则地,如果引用别人地成果或其他公开地资料(包括网上查到地资料),必须按照规定地参考文献地表述方式在正文引用处和参考文献中明确列出.我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛地公正、公平性.如有违反竞赛章程和参赛规则地行为,我们将受到严肃处理.我们授权全国大学生数学建模竞赛组委会,可将我们地论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等).我们参赛选择地题号是(从A/B/C/D中选择一项填写): C我们地参赛报名号为(如果赛区设置报名号地话): Y4904 所属学校(请填写完整地全名):杨凌职业技术学院参赛队员 (打印并签名) :1. 李策2. 路开3. 李延枫指导教师或指导教师组负责人 (打印并签名):张涛(论文纸质版与电子版中地以上信息必须一致,只是电子版中无需签名.以上内容请仔细核对,提交后将不再允许做任何修改.如填写错误,论文可能被取消评奖资格.)日期: 2013 年 9 月 16 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):基于古塔变形问题地数学模型摘要本文主要通过建立数学模型来探讨古塔地变形情况以及未来地变形趋势.首先通过建立解读几何模型确定古塔各层地中心坐标,然后利用Matlab软件进行多项式拟合得到各层中心坐标地曲线方程,最后借助此曲线方程计算得倾斜、弯曲、扭曲等各个变形量,并绘制出各层地位移沉降折线图,通过这些图形地变化趋势并结合各个变形量之间地关系,我们预测出古塔未来地变形趋势.针对问题一:我们根据题中给出地数据和条件,结合对古塔实际观测点,通过Matlab绘图软件确定古塔形状为八角形,从而建立起解读几何模型,并用Excel电子表格计算每层八点坐标地平均值,进而确定各次测量地古塔各层中心坐标.针对问题二:首先由问题一中所计算出地各层中心坐标,对于各个测量年份而言,将三维曲线转换为二维曲线,利用matlab软件对各层中心点坐标进行多项式(曲线)拟合,根据拟合出地曲线,取得该曲线地xyz三个旋转角度,即倾斜(z轴与xy平面地夹角),弯曲(曲线地曲率),扭曲(绕z轴地旋转角度)等,记为α、K、β.针对问题三:利用题中所给数据,绘制各测量年份地各层位移沉降折线图,观察其倾斜趋势,并进行预测;结合问题二中曲线曲率和扭曲角度,联系测量年份,分别利用多项式拟合得到各自与测量年份地关系式,进而更好地预测出弯曲、扭曲地变形趋势.最后,综合分析各个变形量地趋势,并对模型进行评价推广.关键词:中心坐标 matlab软件多项式拟合一.问题重述古塔是一种在亚洲常见地,有着特定地形式和风格地东方传统建筑,是中国五千年文明史地载体之一,为祖国城市山林增光添彩,矗立在大江南北地古塔,被誉为中国古代杰出地高层建筑.[1]古塔由于长时间经过各种自然环境地影响,必然会产生变形.文物部门为了更好地保护古塔,必须对其进行适时地观测,确定各种变形量,根据变形量,预测古塔地变形趋势,最后制定必要地保护措施.因此,根据上述信息,我们讨论以下问题:1、建立数学模型,研究古塔各层中心位置地通用方法,并列表确定各次测量地古塔各层中心坐标.2、分析古塔倾斜、弯曲、扭曲等变形情况.3、综合各种变形情况,分析古塔未来地变形趋势.二.问题分析本文研究地是古塔地变形问题.题中古塔地变形主要包括倾斜、弯曲、扭曲.首先,根据题中给出地数据和条件,确定各次测量地古塔各层中心坐标;然后对各个测量年份依次分析,将三维曲线转换为二维曲线,利用matlab软件对各层中心点坐标进行多项式(曲线)拟合,根据拟合出地曲线,计算倾斜、弯曲、扭曲三个变形量地大小关系;最后绘制各测量年份地各层位移沉降折线图,并分别利用多项式拟合得到各自与测量年份地关系式,从而更好地预测古塔未来地变形趋势.三.模型建设1.假设每层各个点都在同一平面内;2.假设古塔在各种自然环境作用下,不发生破坏;3. 假设倾斜只受地基地沉降影响,忽略其他因素.四.符号说明五.模型建立与求解5.1关于问题一地模型建立与求解:根据题中给出地数据和条件,我们利用Matlab 绘图软件可以得出题中地古塔为八角形古塔:假设每层各个点都在同一个平面内,根据简单地解读几何地方法确定各次测量地古塔各层中心坐标.可得中心坐标(x,y,z )地通用公式:x=887654321x x x x x x x x +++++++y=887654321y y y y y y y y +++++++z=887654321z z z z z z z z +++++++根据上式,用Excel 电子表格计算每层八点坐标地平均值,确定各次测量地古塔各层中心坐标.如表1如下:5.2关于问题二地模型建立与求解:根据问题一,我们得出各次测量地古塔各层中心坐标),,(z y x ,如图1所示:图1由图1,可以看出图中后两点偏差较大,所以拟合时将其忽略.由于中心坐标为三维坐标,所以不能将各层中心坐标进行三维多项式拟合.[2]首先,我们要将三维转换成二维进行计算,令A=22y x +,进而让三维坐标),,(z y x 转换成二维坐标),(z A ;分别作Aoz 面地投影,然后将各层二维坐标进行多项式拟合.拟合程序见附录,拟合图像如图2所示:通过拟合得到:z= 21794.387 A 3-50411386.903A 2+38867927591.030A-9989249763219.082倾斜(z 轴与xy 平面地夹角):对z 求一阶导z '=65383.161A 2-100822773.806A+38867927591.030=tan(α)α=arctan(65383.161A 2-100822773.806A+38867927591.030)弯曲(曲线地曲率):对z 求二阶导z ''=130766.322A-100822773.806=1k 2/32,,,)1(y y + [3]=2/322])1.0303886792759+806A 100822773.- 65383.161A (1[806100822773.-A 130766.322+扭曲(绕z 轴地旋转角度):我们先做出古塔俯视图(即xoy 面地曲线),如图3所示:图3据观察可得出,前10个点基本在同一条直线上,受扭曲地影响较小,所以我们用这10个点可以拟合出一条直线函数作为不受扭曲地参照直线,再连接第一层塔心和塔尖地塔心得到另一条直线,两条直线所成地夹角即为扭曲角度.1986年前十组中心坐标拟合图如图4图4前10点拟合图方程:y= -0.6425x+886.7750同时,我们可以求出连接第一层塔心和塔尖地塔心所得到地另一条直线地方程: >> x=[566.6648,567.2473]。

题目: C参赛队员:队员1王建明队员2程建良队员3杨李指导教师:教练组单位:江西机电职业技术学院承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):C我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):江西机电职业技术学院参赛队员(打印并签名) :1. 王建明2. 程建良3. 杨李指导教师或指导教师组负责人(打印并签名):王广明日期: 2013 年 9 月 15 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):古塔变形问题摘要本文主要分析了古塔因为受自重、气温、风力、地震、飓风的影响产生倾斜、弯曲、扭曲等变形的问题。
问题一通过将每层的点近似在一个平面上,Z 坐标取各层高度的平均值,采用中心点到各点的距离总和最小分别求得各年各层中心点的坐标。
各年各层中心点坐标见附录1.问题二塔的倾斜度通过三维拟合各层的中心点坐标,通过画出散点图,发现1986年与1996年第13层数据异常,我们去除那两点考虑,通过空间三维拟合得到一条直线,然后将直线投影到平面上,直线与在平面上的投影的夹角就是古塔的倾斜角。

(高教社杯全国大学生数学建模竞赛古塔变形的数学模型承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):C我们的参赛报名号为(如果赛区设置报名号的话):13289002所属学校(请填写完整的全名):湖北职业技术学院参赛队员(打印并签名):1.2.3.指导教师或指导教师组负责人(打印并签名):数模组日期:2013年9月13日赛区评阅编号(由赛区组委会评阅前进行编号):高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):此文档收集于网络,如有侵权请联系网站删除古塔变形的数学模型摘要古塔被誉为中国古代杰出的高层建筑物,历史悠久,值得并需要我们的保护。
本文研究了关于古塔变形的问题,古塔的变形与塔身的中心紧密相关,具体分析了古塔倾斜、弯曲、扭曲的变形情况及趋势。
对于问题1,建立中心位置模型,采用多边形组合形心的算法,求的结果是表6,7,8,9中的数据;在问题2-1中,研究塔身的倾斜建立了古塔自身倾斜角的模型和古塔相对倾斜角模型两个数学模型,模型2-1.1利用三角函数相关知识确定倾斜角,结果是1986年的塔身倾斜了1.5308°,1996年的塔身倾斜了1.5558°,2009年的塔身倾斜了1.5564°,2011年的塔身倾斜了1.5339°;模型2-1.2对各年份各层的中心点数据进行空间直线拟合,采用空间向量法计算两直线的夹角,结果是古塔1996年相对于1986年倾斜了0.049°,2009年相对于1996年未发生倾斜,2011年相对于2009年倾斜了0.0245°。

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2013 年 9 月 13 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):对古塔变形问题的数学建模摘要中国古语有云,“救人一命胜造七级浮屠”,所谓浮屠也就是大众口中的“塔”。
在中国辽阔的大地上,古塔的踪影随处可见。
它们造型精美、结构巧妙,成为可多得的独特景观。
早起的古塔,主要是阁楼式的建筑,从唐朝经过两宋至辽、金,是我国古塔发展的高峰时期,特别是唐和两宋,古塔的建造达到了空前繁荣度,总量较以前大增,材料也更为丰富,除了木材和砖、石以外,还使用了铜、铁、琉璃等、材料上有木塔为主转为以石塔为主,平面则由四方形逐渐演变为六角和八角形。

承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员 (打印并签名) :1.2.3. 指导教师或指导教师组负责人 (打印并签。
)日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):古塔的变形保护模型摘要中国古塔是我国古代建筑的杰出,它融合了外来文化与中华建筑的精华,现存的古塔已成为城市的一道风景,是城市历史文化的重要组成部分。
但是,古塔长时间的承受自重、气温、风力等作用,偶然还会遭受自然灾害、地震、飓风等影响,还存在古塔的材料结构整体性差及其他因素使古塔产生了各种形变,倾斜、弯曲、扭曲等。
本文根据以上提出的问题,完成了以下工作首先,分析了附录提供的四年观测数据,画出了每层的观测数据三维图,确定了以观测数据凸多边形的重心模型为塔层中心的方法,确定古塔各层的中心位置及中心坐标,并列出表格。

古塔变形的模型及预测吉耀武【摘要】Pagodas are the key protected cultural relics of our country. In order to protect pagodas ,the cultural relics department surveies progodas to get all kinds of deflections and to draft the necessary protective measures ,by means of four observation data of the cultural relics department,the author firstly supplements the missing data in 1986 and 1996. With the complete data fitting in each layer,each point can be projected on to the flat surface,and the universal model of the center coordinates in each layer is obtained. Linear fitting the center points ,the measurement tilted model is obtained by using the angle of the central axis and the horizontal plane. Cubic spline fitting the center points is carried out,and the measuring bending model is obtained by using the fitted curve curvature at every point,and the measuring distorted model is obtained by using rotation angle of fitting adjacent planes. Finally using MATLAB programming the deformation data of model are calculated ,and the deformation of each layer can be detected,then the reliable basis for the cultural relics departments corresponding measures is established. The model can also be extended to the other structure deformation measurement.%古塔是我国重点保护文物,为保护古塔,文物部门对古塔进行观测,了解各种变形量,以制定必要的保护措施,借用文物部门的4次观测数据,首先对1986年和1996年缺失数据进行补充,利用完整的数据拟合每层各测量点所在平面,将各点投影到平面上,得到每层各中心点坐标的通用模型。
承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):5339所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2013 年 09 月 16 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):古塔的变形数学模型摘要:本文是研究关于古塔变形类型以及变形分析的模型,用Matlab画出古塔的三维结构可以看出它是近似于正八边形的形状。
因此,问题一我们用每层各个测量点坐标的平均值作为塔每层的中心坐标,再用中心坐标的三个坐标值分别对时间t做回归来得到确定古塔各层中心位置的通用方法。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):古塔的变形摘要:本文研究的古塔的变形问题,通过对问题背景及附件资料进行深入地分析,采用数据拟合、求平均值等方法整理出具有科学性的分析数据。
通过对建筑物位移监测数据处理方法的研究, 采用自回归模型对位移监测数据进行处理, 根据建立的模型对具体建筑物的监测点的位移变化量进行预报。
经过计算分析, 根据位移量之间变化的关系而建立的自回归预测模型具备较高的拟合及预测精度,运用三维坐标系和数学软件将古塔的模型以空间模型的形式表现出来,直观且科学,对于研究古塔的变形具有较高的科学性和说服性。
再通过三维坐标之间的回归和三维坐标与时间的回归而分析出古塔的倾斜,弯曲,扭曲等变形状况,通过数学软件的计算及列表列图的方法将结果直观体现,通过大量的计算与分析,运用几何和代数方法将古塔的变形量以数学的方式说明。
对于分析古塔变形趋势中,运用了位移差和位移残差平方公式等量及与时间的关系来说明其变形趋势。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题.我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出.我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性.如有违反竞赛规则的行为,将受到严肃处理.我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):我们所属学校(请填写完整的全名):重庆三峡学院参赛队员(打印并签名) :1.桂宇星2.李绍红3.张京花指导教师或指导教师组负责人(打印并签名):王良伟日期: 2013 年 9 月 16日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):车道被占用对城市道路通行能力的影响摘要随着经济的发展,城市化进程加快,城市机动化越来越明显,家用轿车大幅度增加,交通问题已成为全球的一大主要难题.特别是大城市,发生车辆碰撞的可能性非常大,进而影响到道路的畅通性. 由于城市道路具有交通流密度大、连续性强等特点,车道一旦被占用,就会降低路段所有车道的通行能力,即使时间短,也可能引起车辆排队,出现交通阻塞,如果处理不当,甚至出现区域性拥堵,给城市交通造成很大压力. 本文以交通事故这种异常事件为例,通过观察视频, 对同一交通横断面不同车道的两个交通事故进行数据统计和分析,研究城市道路基本路段内交通事故影响时间、车辆排队长度、事故影响下不同时间段内断面流量变化之间的关系,得到在某种原因堵塞时,能够对车流排队的时间和长度进行客观的估计,为交通管制与控制部门采取交通管制提供了理论依据.针对问题一及视频1,我们将交通事故发生至撤离期间分成19个时间段,分别统计这19个阶段中经过事故横断面的车辆数,并参照城市道路工程设计规范,计算出19个时间段内实际道路交通量与畅通系数,结合Excel 软件绘图,从而获得了直观的反映出道路通行能力变化过程的结果:A 级稳定流(稍有阻滞):18、19组;B 级稳定流(有阻滞、可接受):1、2、7、8、9、10、16、17组;C 级接近非稳定流(阻滞):5、6、12、13、14、15组;D 级非稳定流(阻塞、严重阻滞):3、4组.针对问题二及视频2,类似于问题一所得出的结论,获得视频2中道路通行能力变化过程的结果. 关于视频1和视频2的道路流通量差异方面, 首先通过对不同目标设置权重,建立基于层次分析法的模糊评判关系,从定性上得出了视频1中的堵塞情况严重于视频1;另外,我们选取了事故事件中的部分时间点,结合聚类分析,从定量上也得出了视频1中的堵塞情况严重于视频2.针对问题三, 结合车流波动理论建立了交通事故下车辆排队长度(x )与横断面实际通行能力(2S )、拥堵持续时间(消散时间T )、路段上游车流量(Q )的模型如下1122f 0()S V (1)(T T )S S f K K x Q K QT +=-⨯-,其中f 12V ,,,,T S S f K K K 为参数.针对问题四, 我们将问题三所得出了模型进行非线性回归分析,确定各个参数的值,得出如下数值表达式:123(0.0001 1.0243)/.)(0.3253+).x x x ±⨯⨯y= (-00001其中123y,x ,,x x 分别为排队长度、上游车流量、道路实际通行能力系数、事故持续时间. 给定1x =1500,2x =0.5, y =140, 从而得出事故持续时间3x 的取值为8分钟左右.关键词:模糊评判,聚类分析,流体交通量,排队论,多元非线性回归一、问题重述1.1 问题背景车道被占用是指因交通事故、路边停车、占道施工等因素,导致车道或道路横断面通行能力在单位时间内降低的现象. 由于城市道路具有交通流密度大、连续性强等特点,一条车道被占用,也可能降低路段所有车道的通行能力,即使时间短,也可能引起车辆排队,出现交通阻塞.如处理不当,甚至出现区域性拥堵.车道被占用的情况种类繁多、复杂,正确估算车道被占用对城市道路通行能力的影响程度,将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据.1.2 需要解决的问题(1).根据视频1,描述视频中交通事故发生至撤离期间,事故所处横断面实际通行能力的变化过程.(2). 根据问题1所得结论,结合视频2,分析说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异.(3). 构建数学模型,分析视频1(附件1)中交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系.(4). 假如视频1(附件1)中的交通事故所处横断面距离上游路口变为140米,路段下游方向需求不变,路段上游车流量为1500pcu/h,事故发生时车辆初始排队长度为零,且事故持续不撤离.请估算,从事故发生开始,经过多长时间,车辆排队长度将到达上游路口.二、问题分析对于问题(1),先数出事故C处未发生的时候,单位时间内通过的车辆,求出正常情况下C处的实际通行能力,并以此为基准,然后,再数出发生事故之后单位时间内通过的车辆,并计算出他们的通行量,从而求出其通行率即为畅通系数.从而直观的反映出道路通行能力的变化过程.对于问题(2),题目要求结合问题一所得结论,对视频一条件下车道占用与视频二进行对比,从而说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异.考虑到道路交通是一个复杂的问题,可以通过基于层次分析法的模糊评判定性上进行讨论.又可以抽取事故期间的不同时间点,通过聚类分析,从定量上对两种情况进行讨论.对于问题(3),要求建议一种数学模型分析视频1(附件1)中交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系,可以考虑构造交通流模型,结合车流波动理论进行讨论.对于问题(4),可以考虑对问题三所得出的函数关系式进行参数设定,可以考虑用非线性回归分析法,从而根据所得关系式解出时间.三、模型假设1、假设将所有车辆分为大型车和标准车两大类,大型车的折算系数取1.5,小型车的换算系数取1.0.2、假设在计算车流量时,所依据的道路横截面为一条直线.3、假设在计算车流量时,换算为车流量的标准单位时,可以用单位时间(1秒)的通行量乘以一年中的单位时间数得到.4、不考虑观测误差、随机误差和其他外在因素所产生的误差.5、假设车辆流在短时间内为连续流.四、变量与符号说明C一条车道的基本通行能力L连续车流的车头间距C n 条车道的基本通行能力y排队长度1x车流量2x横断面通行能力系数车流量3x持续时间五、模型建立与求解5.1 问题(1)的分析、模型建立与求解5.1.1建模准备5.1.1.1.一条车道的基本通行能力首先假设道路和交通状况都处于理想条件下,用技术性能相同的一种标避车,以最小的车头间距连续行驶的理想交通流,在单位时间内通过道路断面的最大车辆数,即基本通行能力,也称为理论通行能力,因为它是假定理想条件下的通行能力,实际上不可能达到.在一条车道连续行驶的车流中,跟随运行的前后相邻两车的间隔距离,即从前车的前端到后车的前端的间隔距离,叫车头间隔.车头间隔可用距离或行车时间来表示,用距离来表示车头间距的称为车头间距(m);用行车时间来表示车头间隔的称为车头时距(s). 路段上一条车道的通行能力,可按车头间距和车头时距两种方法来计算.其计算公式为0100040.3656+L+L.CL L ⨯==反车安,式中:C——一条车道的基本通行能力(pcu/h); v——行驶速度(km/h);L——连续车流的车头间距(m);L安——车辆安全车间距(m);L车——车辆的本身长度(m);L反——驾驶员在反应时间内车辆行驶的距离(m),=vL T反,T=1.2s 左右.由于基本通行能力计算时不考虑道路和交通条件的影响,因此多车道的基本通行能力可按下式计算:0C NC =,式中: N ——车道数;C ——n 条车道的基本通行能力; 0C —一条车道的基本通行能力.为了简化模型,由视频一的数据,我们观察了不同的10辆车在畅通条件下,我们把这10辆车通过通过折算率转换成标准车,如下表所示:. 车型 中 中 小 大 大 小 大 中 小 中 距离 240 240 240 240 240 240 240 240 240 240 时间 17 15 27 25 30 26 25 17 26 18 速度 50.82 57.6 32 34.56 28.8 33.23 34.56 50.82 33.23 48 算出平均值为:40.36标准车的长度为5.3m ,人的反应时间为1.2s ,反应距离为48.432 ,车辆安全车间距2m ,所以L= 56 m.其中 01000V C L==100040.3656⨯=720 .5.1.1.2多车道对路段通行能力的影响自路中心线起第一条车道的折减系数a 条为1.00,第二条车道为0.80~0.89, 第三条为0.65~0.78.其第二车道和第三车道可取中间值分别为0.85,0.72. 车道宽度3.25m ,通行能力折减系数0.94 按《道路通行能力分析》a 交=0.81)·(·C C a a a =理论交折道; 因此,1C =9460.810.94⨯⨯=720 ;2C =9460.850.810.94⨯⨯⨯=612 ; 3C =9460.720.810.94⨯⨯x=518 .故C 路段=1840pcu/h. 5.1.2数据的统计预处理观察视频一,我们将车辆发生碰撞到交通通畅的这一段时间分为24段,通过统计通过事故横断面的车辆,并转化为标准车辆数可得以下表格:车辆统计表1时间点 通过大车量 通过小车量当量车 堵车前1 1 1314.52 1 19 20.53 3 1822.5 4 4 14 20 5 1 14 15.5 6 0 13 13 7 1 1314.5堵 车 中8 0 14 14 9 1 18 19.5 10 0 13 13 11 1 8 9.5 12 0 14 14 13 1 14 15.5 14 1 15 16.5 15 1 14 15.5 16 1 14 15.5 17 0 14 14 18 1 11 12.5 19 2 9 12 20 1 10 11.5 21 2 11 14堵车后22 2 22 2523 0 20 20 24 1 23 24.55.1.3新物理量的创立与指标的分级仿照交通最大服务量pcu/(km*ln)我们创建新的物理量车道交通量pcu/(h*ln),通过对附件3道路实际路宽及车道数的了解, 参照PHF 即高峰小时的计算式:PHF=小时交通量/交通流率(该小时).对于1min 区间来说,1.60VPHF V =⨯式中: V ——小时交通量;1V ——高峰小时内最大的60min 交通量.我们定义新的物理量:通畅系数=实际车道交通量/标准车道交通量 化为当量车的表格如下:时间点 当量车 车道交通量 通畅系数 堵车前 70 377 堵 车中1 20 1191.6 0.79442 15.5 1143.45 0.7623 3 13 875.1 0.5834 4 14.5 871.8 0.5812 5 14 1045.65 0.69716 19.5 1024.65 0.68317 13 1135.95 0.75738 9.5 1113.9 0.7426 9 14 1197.45 0.7983 10 15.5 1164.3 0.7762 12 16.5 1017 0.6780 13 15.5 969.3 0.6462 14 15.5 1015.5 0.677015 14 981.45 0.654316 12.5 1136.850.7579 17 12 1122.3 0.7482 18 11.5 1368.6 0.9124 19 14 1494 0.9960 堵车后60 588通畅系数波动图由车道交通量分析同一时间通过同一车道的车辆越多则车道越通畅,因而通畅系数越大则表明道路通行能力越高,我们对通畅系数进行分级从而更加直观看出道路通行状况如下表所示: A 级稳定流(稍有阻滞) B 级稳定流 (有阻滞、可接受) C 级接近非稳定流 (阻滞) D 级非稳定流 (阻塞、严重阻滞)0.9—1.0 0.7—0.9 0.6—0.7 0.6及以下 第18,19组第1、2、7、8、9、10、16、17组 第5、6、12、13、14、15组第3、4组5.2 问题(2)的求解 5.2.1 问题(2)的分析根据问题1所得结论,结合视频2,我们采用了模糊评判模型和聚类分析模型分析说明同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异. 5.2.2模糊评判模型的建立与求解}{12u u ,...,u s n U =第一步,将因数集,将某种属性分为个子因素集12,,s U U U ⋯,其中i U = {i2ini i1u u ,...,u },, i=1,2s ,...,,且满足○1 12s n +n +...n =n; ○2 12...;S U U U ⋃⋃⋃= ○3 i j i j =φ≠⋂对任意的,U U . 第二步,对每一个因素集U i ,分别做出综合评判.设12{}m V v v v =⋯,,,为评语集,i U 中各因素相当于V 的权重分配是[]12,,.i i i ini A a a a =⋯若i R 为单因素评判矩阵,则得到一级评判向量i i i i1i2im ==[b ,b ,...n ],i=1,2,...,s.B A R第三步,将每个i U 看作一个因素,记为 12{,,...,}.s k u u u =这样,K 又是一个因素集,K 的单因素评判矩阵为11112122122212.m m S s s sm B b b b B b b b R B b b b ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦将每个单因素看作一个矩阵,,按其重要性分配权重1[,...,]s A a a =,于是得到二级评判向量,1[...].m B A R b b =∙=在本问题中,一级指标对目标值对应的权重0.4,0.6.,在视频一的条件下,车道一、车道二,车道三对应的权重为0.5,0.25,0.25.在视频二对应的条件下,车道一、车道二,车道三对应的权重为0.25,0.5,0.5. 视频1表格如下: 视频1情况下的模糊评判指标一级指标 二级指标 优 良 中 合格 差拥堵截断面的大型车辆 车道一 0.1 0.3 0.4 0.1 0.1车道二 0.2 0.4 0.4 0 0车道三 0.1 0.3 0.5 0.1 0 拥堵截断面中的小型车辆 车道一 0 0.1 0.1 0.4 0.4车道二 0 0 0.1 0.4 0.5车道三 0.2 0.4 0.3 0.1 0结果:B A R =∙=[0.0950 0.2550 0.3150 0.1750 0.1600] 根据最大隶属度原则,评判结果为中. 视频2表格如下:视频2情况下的模糊评判指标一级指标 二级指标 优 良 中 合格 差拥堵截断面的大型车辆 车道一 0.1 0.3 0.4 0.2 0车道二 0 0.4 0.2 0.2 0.2车道三 0.2 0.3 0.4 0.1 0 拥堵截断面中的小型车辆车道一 0.1 0.1 0.1 0.4 0.3车道二 0.1 0.1 0.1 0.4 0.3车道三 0.2 0.4 0.2 0.1 0.1结果:B A R =∙==[0.1350 0.2950 0.2700 0.1900 0.1100] 根据最大隶属度原则,评判结果为良好. 结论分析:由模糊评判从定量上可以得出,视频一条件下道路情况要比视频二糟糕. 5.2.3聚类分析模型的建立与求解聚类分析主要包括样本相似性度量,类与类间相似性度量两个步骤. (1)样本的相似性度量在对样本进行聚类分析时,首先要确定样本的相似性度量,常用的样本相似性度量有马氏距离、车比雪夫距离、欧式距离等,下面介绍最常用的欧式距离法.记Ω是样本点集,距离),(y x d 是+→×R ΩΩ的一个函数,满足条件: ①;∈,,0≥),(Ωy x y x d②;=0=),(y x y x d 当且仅当 ③;∈,),,(=),(Ωy x x y d y x d ④.∈,,),,(+),(≤),(Ωz y x y z d z x d y x d这一距离的定义满足正定性、对称性和三角不等式.在聚类分析中,对于定量变量,最常用的是闵氏距离,即,0,]||[),(11>==q y x y x d qpk q k k q ∑-当2=q 时则得到欧式距离. (2)类与类间的相似性度量如果有两个样本类1G 和2G ,则可以用最短距离法、最长距离法、重心法、类平均法等方法度量它们之间的距离.下面介绍本文应用的类平均法.,),(*1),(122121∑∑∈∈G x G x j i i j x x d n n G G D = 它等于21,G G 中两样本点距离的平均,21,n n 分别为21,G G 中的样本点个数.下面选出的指标对酿酒葡萄样品进行聚类分析.首先对每个指标的数据ij p 进行标准化处理得到ijp ~,,,2,1,,,2,1,~n j m i s μp p jjij ij ===-其中,∑mi ij j p m μ11==,∑--m i j ij j μp m s 12)(11==,n j ,,2,1= ,n m ,分别表示选取的样点的数量和指标的数量.求解结果:样本间相似性采用欧式距离度量,类间距离的计算选用类平均法.视频1中我们收集的数据如下表所示:时间点 通过大车量 通过小车量 1/(该时刻区域内小车数目) 1/(该时刻区域内大车数目) 一车道车的数量/总车数1 1 13 0.07142857 1 0.33333333321 19 0.0555555561 0.43 3 18 0.071428571 0.33333333 0.6666666674 4 14 0.045454545 0.5 0.2857142865 1 14 0.05 1 0.256 0 13 0.055555556 0 0.27 1 13 0.066666667 1 0.31258 0 14 0.052631579 0 0.3030303039 1 18 0.071428571 1 0.2510 0 13 0.055555556 0 0.22222222211 1 8 0.071428571 1 0.2702702712 0 14 0.052631579 0 0.27777777813 1 14 0.043478261 1 0.32258064514 1 15 0.043478261 0.5 0.32258064515 1 14 0.037037037 0.5 0.27777777816 1 14 0.038461538 0.5 0.2702702717 0 14 0.035714286 1 0.29411764718 1 11 0.041666667 1 0.24390243919 2 9 0.05 1 0.29411764720 1 10 0.055555556 0 0.2702702721 2 11 0.0625 0 0.42 22 0.0625 0.5 0.41666666723 0 20 0.076923077 1 0.45454545524 1 23 0.083333333 1 0.666666667划分成3类的结果如下:第1类的有11 18 19 20 21第2类的有1 4 5 6 7 8 10 12 13 14 15 16 17第3类的有2 3 9 22 23 24**********************************划分成4类的结果如下:第1类的有22 24第2类的有2 3 9 23第3类的有11 18 19 20 21第4类的有1 4 5 6 7 8 10 12 13 14 15 16 17**********************************划分成5类的结果如下:第1类的有4第2类的有1 5 6 7 8 10 12 13 14 15 16 17第3类的有22 24第4类的有2 3 9 23第5类的有11 18 19 20 21聚类分析结果运行图视频2中我们收集数据如下所示:时间序号通过大车量通过小车量1/(该时刻区域内小车数目)1/(该时刻区域内大车数目)一车道车的数量/总车数1 2 19 0.1 0.5 0.3333332 1 18 0.05 1 0.3333333 0 20 0.1 0 0.6666674 3 13 0.046666667 0.333333 0.2857145 1 12 0.066666667 1 0.256 0 13 0.046666667 0 0.37 1 15 0.043478261 1 0.328 0 15 0.033333333 0 0.219 1 12 0.043478261 1 0.2510 0 13 0.056923077 0 0.22222211 1 14 0.041428571 1 0.2702712 0 15 0.047619048 0 0.27777813 1 15 0.043478261 1 0.32258114 1 14 0.043478261 1 0.32258115 0 13 0.037037037 0 0.27777816 1 10 0.038461538 1 0.2702717 0 12 0.035714286 0 0.29411818 2 13 0.041666667 0.5 0.24390219 1 17 0.05 1 0.29411820 0 17 0.055555556 0 0.2702721 1 18 0.0625 1 0.422 2 20 0.083333333 0.5 0.45454523 0 20 0.1 0 0.66666724 1 19 0.083333333 1 0.625划分成3类的结果如下:第1类的有16第2类的有4 5 6 7 8 9 10 11 12 13 14 15 17 18第3类的有1 2 3 19 20 21 22 23 24**********************************划分成4类的结果如下:第1类的有7 8 11 12 13 14第2类的有4 5 6 9 10 15 17 18第3类的有16第4类的有1 2 3 19 20 21 22 23 24**********************************划分成5类的结果如下:第1类的有2 19 20 21第2类的有1 3 22 23 24第3类的有7 8 11 12 13 14第4类的有4 5 6 9 10 15 17 18第5类的有16聚类分析结果运行图5.2.4模型评判由以上计算可知,多车道道路通行能力从中心至边缘车道依次递减.视频一中撞车位置在距道路中心一、二条车道上,因而可行车道为第三条车道;视频二中撞车位置在距道路中心二、三条车道上,因而可行车道为第一条车道.而从计算中可得,可上述结论,即视频二的事故所处断面实际通行能力要比视频一要强.这与实际情况比较吻合。
确定古塔中心坐标的通用方法及MATLAB程序【摘要】2013年全国大学生数学建模竞赛C题是借用文物部门的4次观测数据研究某古塔的倾斜、弯曲、扭曲等变形情况。
但是要研究其变形情况,必须先确定古塔各层的中心坐标。
本文首先对1986年和1996年缺失数据进行补充,其次,利用完整的数据拟合每层各测量点所在平面;最后,将各测量点投影到平面上,得到每层各中心点坐标的通用模型。
并且每一步都附有相应的MATLAB 计算成程序,这样做极大的减少了计算量,加快了运算速度。
【关键词】中心坐标;线性拟合;平面拟合一、问题提出2013年全国大学生数学建模竞赛已经结束了,但对竞赛题目的研究还在继续,其中C题是根据附件1提供的4次观测数据研究某古塔的倾斜、弯曲、扭曲等变形情况以及该塔的变形趋势。
但是要研究其变形情况,必须先确定古塔各层的中心坐标,那么中心坐标该如何确定,大量的数据计算又该如何处理呢?二、问题解决1.缺失数据补充附件1(参见2013年全国大学生数学建模竞赛C题)给出的数据中,1986 年和1996 年的第13层第5点的坐标是缺失的,要完整的讨论各层的中心坐标,我们需要补充缺失数据。
首先,提取1986年古塔前12层第5点的坐标,分别作x,y,z与层数t的散点图(如图1所示)。
程序如下:A=[567.941 517.407 1.772;567.995 517.563 7.306;568.048 517.716 12.741;568.091 517.838 17.064;568.136 517.969 21.705;568.18 518.095 26.189;568.172 518.346 29.791;568.164 518.59 33.305;568.156 518.834 36.809;568.148 519.068 40.171];t=(1:12)’;x=A(:,1);y=A(:,2);z=A(:,3);subplot(2,2,1);plot(t,x,’*’),grid onsubplot(2,2,2);plot(t,y,’o’),grid onsubplot(2,2,3);plot(t,z,’+’),grid on图1 1986年每层第5点的坐标分量散点图其次,再观察图1中x坐标发现:x与层数t呈现分段线性关系,我们所求的第13层坐标处于分段函数第三段上,所以我们只需对第三段用MATLAB进行数据拟合[1],程序如下:t1=[ones(3,1),(10:12)’];x=A(10:12,1);[b1,bint1,r1,rint1,stats1]=regress(y,t1)由该程序可得x坐标与层数t的第三段线性关系为:x=568.6932-0.0545t(t≥10)(1)第三,观察图1中y坐标与z坐标发现:y,z与层数t是线性关系,所以我们用MATLAB对坐标数据进行线性拟合,程序如下:t2=[ones(12,1),(1:12)’];y=A(:,2);[b2,bint2,r2,rint2,stats2]=regress (y,t2)t3=[ones(11,1),(2:12)’];z=A(2:12,3);[b3,bint3,r3,rint3,stats3]=regress (z,t3)由该程序可得y和z坐标与层数t的线性关系为:y=517.1185+0.1880t (2)z=0.8997+4.0044t(由于第1点是异常点,所以剔除掉)(3)最后,我们在(1)-(3)式中分别令t=13可得1986年第13层第5点的坐标为:(567.9847,519.5625,52.9569)。
古塔的变形摘要古塔是我国独具代表性的建筑种类之一,它展现着我国悠久的历史文化,也向世界展示着我国古代独特的建筑特色和精湛的建筑技术。
但由于古塔长时间承受自重、风力、温度等各种作用,以及地震、台风、暴雨等自然灾害的影响,古塔会产生倾斜、弯曲、扭曲等变形。
本文根据测绘公司先后在1986年、1996年、2009年和2011年对古塔进行的四次观测得到的数据,分析古塔的倾斜、弯曲和扭曲等变形情况,并对古塔的变形趋势进行预测。
首先,本文通过最小二乘法建立数学优化模型,拟合出古塔各层的中心点。
利用MATLAB编程求出各层中心点坐标的通用方法及各层中心点坐标。
其次,利用空间曲线拟合和MATLAB编程分析古塔的倾斜、弯曲和扭曲等变形情况。
最后,根据古塔的倾斜、弯曲和扭曲程度来分析古塔的变形趋势。
关键词:数学模型最小二乘法空间拟合 MATLAB目录1. 问题重述 (1)1.1背景知识 (1)1.2需解决的问题 (1)1.3相关数据 (1)1.4课题来源 (1)2. 问题分析 (2)2.1对问题的总体分析 (2)2.2对问题的具体分析 (2)2.2.1对问题一的分析 (2)2.2.2对问题二的分析 (2)2.2.3对问题三的分析 (2)3.模型假设 (3)4.符号说明 (3)5.模型准备 (3)5.1对建筑物变形和相关术语的说明 (3)5.2对遗失数据的预测 (4)6.模型的建立与求解 (5)6.1问题一的分析与求解 (5)6.1.1建立模型的思路 (5)6.1.2空间平面拟合 (6)6.1.3确定中心点位置 (8)6.2问题二的分析与求解 (12)6.2.1建立模型的思路 (12)6.2.2空间直线拟合 (12)6.2.3倾斜程度分析 (16)6.2.5扭曲程度分析 (19)6.3问题三的分析与求解 (21)6.3.1倾斜趋势预测 (21)6.3.2弯曲趋势预测 (22)6.3.3扭曲趋势预测 (23)参考文献 (24)附录 (25)1. 问题重述1.1 背景知识古塔是我国独具代表性的建筑种类之一,它展现着我国悠久的历史文化,也向世界展示着我国古代独特的建筑特色和精湛的建筑技术。
古塔的变形情况及趋势研究发表时间:2014-11-21T13:42:22.750Z 来源:《价值工程》2014年第5月上旬供稿作者:王飞[导读] 本文通过问题转化,建立初等数学模型研究古塔的倾斜程度、弯曲程度及扭曲程度。
Study on Deformation and Tendency of Old Pagoda王飞 WANG Fei;章茜 ZHANG Qian(浙江机电职业技术学院,杭州 310018)(Zhejiang Institute of Mechanical & Electrical Enginnering,Hangzhou 310018,China)摘要:依据2013年全国大学生数学建模竞赛C题所给的古塔各层中观测点坐标的信息,运用基于最小二乘法的椭圆拟合算法结合MATLAB软件,列表给出各次测量的古塔各层中心坐标。
利用古塔各层中心坐标,并将问题进行转化,采用初等数学模型研究古塔的倾斜程度、弯曲程度、扭曲程度,最后建立灰色预测模型GM(1,1),对上述引起古塔变形的三个因素进行拟合、预测,分析古塔的变形趋势。
Abstract: According to coordinates of points observed for each layer of ancient pagoda in problem C of Chinese Undergraduate Mathematical Contest in Modeling(2013), this article lists the measured coordinates of the center of each layer in old pagoda by using ellipse fitting method which based on least-square principle and MATLAB. The problem is transformed by using the coordinates of the center of old pagoda in each layer, when the tilting degree, bending degree, twisting degree of old pagoda can be studied through primary mathematics model. Finally, the paper establishes the gray prediction model GM(1,1), summarizes and predicts the three factors which caused the deformation of old pagoda, and analyzes its trend.关键词:古塔变形;中心坐标;倾斜角;灰色预测模型GM(1,1)Key words: deformation of old pagoda;central coordinate;inclination;the gray prediction model GM (1,1)中图分类号:TU196;O242.1 文献标识码:A 文章编号:1006-4311(2014)13-0212-030 引言目前现存数量不多的古塔是一种古代高层建筑,标志着古代人们征服自然的胜利。
2013高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)
C题古塔的变形
由于长时间承受自重、气温、风力等各种作用,偶然还要受地震、飓风的影响,古塔会产生各种变形,诸如倾斜、弯曲、扭曲等。
为保护古塔,文物部门需适时对古塔进行观测,了解各种变形量,以制定必要的保护措施。
某古塔已有上千年历史,是我国重点保护文物。
管理部门委托测绘公司先后于1986年7月、1996年8月、2009年3月和2011年3月对该塔进行了4次观测。
请你们根据附件1提供的4次观测数据,讨论以下问题:
1. 给出确定古塔各层中心位置的通用方法,并列表给出各次测量的古塔各层中心坐标。
2. 分析该塔倾斜、弯曲、扭曲等变形情况。
3. 分析该塔的变形趋势。