第四章 谐振子
- 格式:ppt
- 大小:812.50 KB
- 文档页数:33


谐振子的能级特性与对称性分析陈绍敏(湖北大学物理学与电子技术学院 2002级物理学)引 言在经典力学中,谐振子是被约束在一根轴线上运动的粒子,作用在它上的是恢复力,它与粒子的位移成正比,它的解是众所周知的,它的运动是一种正弦运动,它在原点附近振荡,相应的量子力学问题是质量为μ,角频率为ω的一维粒子具有哈密顿量)(212222q P H ωμμ+=的问题,位置变量q 和动量p 由对易关系i p q =],[联系本文将研究质量为μ的k 维粒子上有哈密顿量∑=+=ki i i q p H 12222)(21ωμμ的问题,特别是将用群论观点来研究谐振子的能级简并度特性与对称性分析。
§1 二维各向同性谐振子的态函数及能级特性(1)采用平面极坐标,二维谐振子势能2221)(ρμωρ=V(1)Schrödinger 方程为ψ=ψ⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂-E 22222221112ρμωϕρρρρρμ (E>0) (2) 令 )(),(ρϕρϕR e im =ψ(3)采用自然单位1===ωμ ,自然单位中各特征量如下 谐振子势中的特征量则径向方程表示为0)()2(122222=⎥⎦⎤⎢⎣⎡-+-+ρρρρρρR E m d d d d (E>0) (4)0→ρ时变为0)(12222=⎥⎦⎤⎢⎣⎡-+ρρρρρR m d d d d (可参看径向方程的解在奇点0=r 邻域的行为) 令s R ρ∝,代入上式,得022=-m s所以 ||s m =±可以证明,0→ρ时渐进行为||m R -∝ρ的解是物理上不能接受的,予以抛弃,故||)(m R ρρ∝ )0(→ρ当∞→ρ,得0)(222=⎪⎪⎭⎫ ⎝⎛-ρρρR d d 所以[]2/exp )(2ρρ±∝R ,而满足束缚态边界条件的解只能取2()exp 2R ρρ⎡⎤∝-⎣⎦,所以 ||2()exp 2()m R u ρρρρ⎡⎤=-⎣⎦代入(11)式,得()0]1||22[21||222=+-+⎪⎪⎭⎫ ⎝⎛-++u m E d du m d u d ρρρρ (5) 再令 2ρξ=(6) 得 ()0221||1||22=⎥⎦⎤⎢⎣⎡---++u E m d du m d u d ξξξξ(7)上式是合流超几何方程,它在0=ξ邻域的解析解表为),,(ξγαF ,相应参数为 221||E m -+=α1||+=m γ(8)束缚态边界条件要求,221||ραn Em -=-+=,2,1,0=ρn所以二维各向同性谐振子的能量本征值为)1||2(++=m n E ρ(自然单位)或 ,2,1,0||2),1(=+=+=m n n n E n ρ (9)未归一化的波函数为),1||,(),(2||ρρϕρψρϕρ+-∝m n F e m im m n(10)不难求出能级n E 的简并度为,3,2,1)1(=+=n f n(11)(2)二维各向同性谐振子还可以分解成二个彼此独立的一维谐振子,采用直角坐标,因各向同性,其振子强度0ωωω==y x ,故()222021y x V +=μω 相应的能量 002121ωω ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=y x n n n n E yx0)1(ω +=n E n y x n n n +=,2,1,0,,=n n n y x对于给定n ,有n n x ,2,1,0=相应的 0,2,1, --=n n n n y所以有)1(+n 个量子态y x n n ψ,能级n E 的简并度为)1(+=n f n 2,1,0=n与(11)式同关于能级简并度与对称性的关系,前人指出过,系统出现简并,往往意味着与Hamilton 量的对称性相联系。



1、填空题1、双原子分子刚性转子模型主要内容:原子核体积是可以忽略不计的质点;分子的核间距不变;分子不受外力作用。
2、谐振子模型下,双原子分子转动光谱选律为:极性分子,3、谐振子模型下,双原子分子振动光谱选律为:极性分子,谱线波数为:。
4、刚性转子模型下,转动能级公式为。
5、谐振子模型下的双原子分子能量公式为,其中特征频率为6、分子H2,N2,HCl,CH4,CH3Cl,NH3中不显示纯转动光谱的有:H2,N2,不显示红外吸收光谱的分子有: H2,N2,CH4。
二、选择题1、已知一个双原子分子的转动常数B(波数单位),纯转动光谱中第二条谱线的波长为( D )?(A)B/4(B)B/2(C)1/6B(D)1/4B解:2、HCl分子的正则振动方式共有( B )种?线性3N-5 非线性3N-6(A)0(B)1(C)2(D)3CO2分子的正则振动方式共有( D )种?(A)1(B)2(C)3(D)4HCN分子的正则振动方式共有( D )种?(A)1(B)2(C)3(D)4对H2O而言,其平动、转动、振动自由度分别为( A )(A)3,3,3(B)3,2,4(C)3,2,3(D)1,2,33、已知一双原子分子转动光谱的第四条谱线在80cm-1,则第九条谱线位置为( D )?(A)120cm-1(B)140cm-1(C)160cm-1(D)180cm-14、运用刚性转子模型处理异核双原子分子纯转动光谱,一般需知几条谱线位置(J),可计算其核间距( B )(A)5 (B)2 (C)3 (D)45、红外光谱(IR)由分子内部何种能量跃迁引起( D )(A)转动(B)电子-振动(C)振动(D)振动-转动6、H2和D2的零点能比值为:( B )(A)1 (B)(C)(D)不确定四、计算题1、已知HCl的纯转动光谱每二谱线间的间隔为20.8cm-1,试求其键长。
解:2、已知1H79Br在远红外区给出了间隔为16.94cm-1的一系列谱带,计算HBr的平衡核间距。

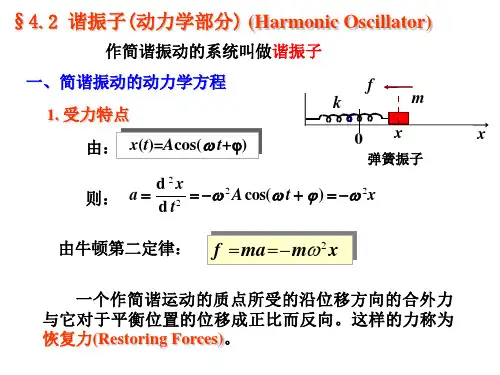
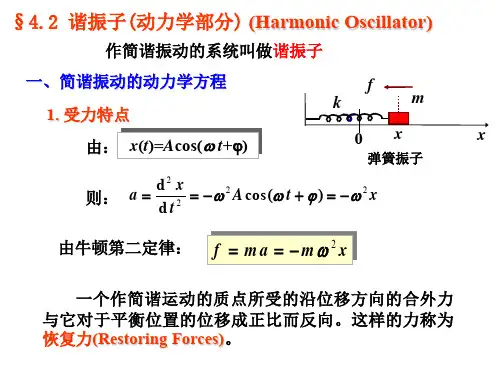
谐振子运动方程谐振子是物理学中一个重要的模型,用于描述有固定平衡位置的物体在受到力的作用下的振动。
谐振子在很多领域都有应用,比如机械振动、电路振荡以及量子力学等。
通过对谐振子的研究,可以深入理解振动的特性和规律。
谐振子的运动方程是描述谐振子振动的基本方程。
在经典力学中,一个简单的谐振子由质点和弹簧组成,并且假设没有外力作用。
谐振子的运动方程可以通过牛顿第二定律推导出来。
我们假设一个质量为m的质点沿着一条直线上运动,它与原点处的一个弹簧相连接。
弹簧的劲度系数为k,原点是谐振子的平衡位置。
当质点偏离平衡位置时,弹簧会施加一个与质点位移成正比的力。
根据胡克定律,弹簧对质点的作用力可以表示为F = -kx,其中F是作用在质点上的力,x是质点的位移。
根据牛顿第二定律,当质点受到的合力不为零时,它将加速度。
因此,我们可以得到方程m*a = -k*x,其中a是质点的加速度。
由于加速度是位移的二阶导数,我们可以将运动方程改写为二阶微分方程m*x'' = -k*x。
这是一个关于位移x的二阶常微分方程,解此方程即可得到谐振子的运动方程。
我们假设解的形式为x(t) = A*cos(ωt + φ),其中A是振幅,ω是角频率,φ是相位常数。
将上述解代入运动方程中,我们可以得到ω的表达式。
由于二阶导数为负号,我们可以得到方程-m*ω^2*A*cos(ωt + φ) = -k*A*cos(ωt + φ)。
两边化简后得到-m*ω^2 = -k,即ω =sqrt(k/m)。
从上述解中可以看出,谐振子的振动是一种简谐运动,即振幅不变、频率恒定的振动。
在运动过程中,质点在平衡位置附近往复振动,通过正弦函数描述运动曲线。
谐振子在物理学中有很多应用。
在机械振动中,谐振子可以用来模拟弹簧振子、摆锤等物体的振动。
在电路中,电感和电容组成的电路也可以看作谐振子。
此外,在量子力学中,谐振子是描述原子和分子的振动性质的重要模型。
总结起来,谐振子的运动方程是一个关于位移x的二阶微分方程。

力学基本模型(四)谐振子模型一、基础篇二、应用篇【例题1】两个木块A 和B 的质量分别为m A =3kg ,m B =2kg ,A 、B 之间用一轻弹簧连接在一起。
A 靠在墙壁上,用力F 推B 使两木块之间弹簧压缩,地面光滑,如图所示。
当轻弹簧具有8J 的势能时,突然撤去力F 将木块B 由静止释放。
求:(1)撤去力F 后木块B 能够达到的最大速度(2)木块A 离开墙壁后,弹簧能够具有的弹性势能的最大值【例题2】如图甲所示,一轻弹簧的两端与质量分别为m 1和m 2的两物块A 、B 相连接,并静止在光滑的水平面上.现使A 瞬时获得水平向右的速度3m/s ,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得A .在t 1、t 3时刻两物块达到共同速度1m/s ,且弹簧都是处于压缩状态B .从t 3到t 4时刻弹簧由压缩状态恢复到原长C .两物体的质量之比为m 1∶m 2=1∶2D .在t 2时刻A 与B 的动能之比为E k1∶E k2=1∶8-v 甲B【例题3】两个木块A和B的质量分别为m A=2kg,m B=3kg,木块A的右侧连有轻质弹簧。
某时刻,木块B以p=6kg·m/s的动量水平向左运动,碰到弹簧后立即与弹簧粘连,不计一切摩擦。
则下列说法正确的是()A.整个过程中,墙壁对A的冲量大小为12N·sB.木块A离开墙壁后,弹簧具有的弹性势能的最大值为1.6JC.木块A离开墙壁后,木块B的最小速度为0.4m/sD.木块A离开墙壁后,它的最大速度为2.4m/s【练习】如图所示,质量分别为m和2m的A、B两个木块间用轻弹簧相连,放在光滑水平面上,A紧靠竖直墙。
用水平力向左推B,将弹簧压缩,推到某位置静止时推力大小为F0,弹簧的弹性势能为E。
在此位置突然撤去推力,下列说法中正确的是()A.撤去推力的瞬间,B的加速度大小为F0 2mB.从撤去推力到A离开竖直墙之前,A、B和弹簧组成的系统动量不守恒,机械能守恒C.A离开竖直墙后,弹簧的弹性势能最大值为E 3D.A离开竖直墙后,弹簧的弹性势能最大值为E。

量子力学中的谐振子量子力学中的谐振子是一种基础的量子力学系统,它在研究原子、分子和固体物质等领域有着重要的应用。
本文将介绍谐振子的基本概念、数学描述以及其在量子力学中的应用。
1. 谐振子的基本概念谐振子是指一个物理系统在平衡位置附近发生振动时,满足线性回复定律的系统。
它的运动可以用势能函数的二次项来描述。
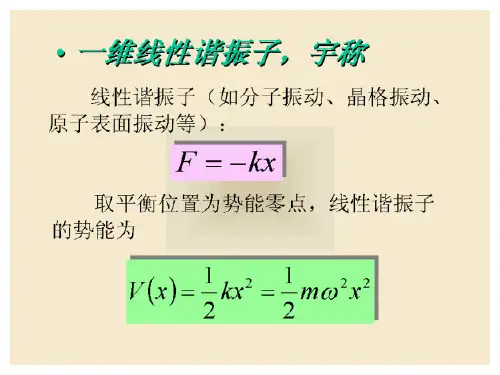
在量子力学中,谐振子的势能函数可以写为:V(x) = 1/2 kx^2其中V(x)表示势能,k为弹性常数,x为谐振子的位移。
谐振子的基态能量为零,且能级是等间隔的。
谐振子的能量具有量子化特性,其能级公式为:E_n = (n + 1/2)ħω其中E_n表示第n级能量,ħ为约化普朗克常数,ω为谐振子的频率。
2. 谐振子的数学描述谐振子的数学描述可以通过谐振子算符实现。
谐振子算符包括产生算符a^+和湮灭算符a,它们满足以下关系:[a, a^+] = 1谐振子的波函数可以用谐振子算符的本征态表示,即:a|n⟩= √n|n-1⟩a^+|n⟩= √(n+1)|n+1⟩其中|n⟩表示第n级本征态。
谐振子算符的本征态是谐振子算符的共同本征态,同时也是能量算符的本征态。
谐振子算符和能量算符之间的关系可以通过谐振子算符的乘积表达:N = a^+ aH = (N + 1/2)ħω其中N为数算符,H为能量算符。
3. 谐振子的应用谐振子在量子力学中有着广泛的应用。
以下介绍谐振子在原子、分子以及固体物质领域的应用。
在原子物理学中,谐振子模型可以用来描述氢原子中电子围绕原子核的振动。
谐振子模型能够计算出氢原子的能级和波函数,从而揭示电子在氢原子中的行为。
在分子物理学中,谐振子模型可以用来描述化学键的振动。
例如,当分子中的原子围绕键的平衡位置发生微小的振动时,可以使用谐振子模型来计算分子的振动能级和谱带。
在固体物理学中,谐振子模型被广泛应用于描述固体中的晶格振动。
固体中原子的排列形成了晶格结构,晶格振动对于固体的热性质、导电性等起着重要作用。
自由谐振子
自由谐振子
自由谐振子是一种重要的现代物理实验装置,是由一个物理固体构成的模型系统,以及一个信号输出仪表和控制系统。
它可以被用来研究可以被模拟的系统的动力学行为。
它的运作原理是:当物理固体被外力激励时,就会发生振动和震荡,信号输出仪表可以观测到这些振动和震荡,并通过合适的控制系统将其转换为相应的电信号输出。
自由谐振子的主要用途有两个:一是用来研究不同系统的动力学特性,如振动机械系统、声学系统等;二是用来研究由不同模型系统组成的复杂系统,这种系统经常被应用到电子学和控制系统等方面。
自由谐振子在物理与工程学方面有很广泛的应用,可以用来研究不同系统的动力学特性和性能,也可以用来调整和控制复杂系统的动力学行为。
自由谐振子是一种物理实验手段,其使用简单,实验效果可靠,而且具有可扩展性。
它不仅可以用于物理分析,还可用于工程学、信息学、机械工程等因素的分析。
自由谐振子的应用广泛,有助于加快人们对许多实际问题的理解和解决,对于科技的发展也有重大意义。