16 4一维谐振子问题
- 格式：ppt
- 大小：837.00 KB
- 文档页数：33
下载文档原格式
合集下载
lecture9 一维谐振子问题波动力学
1 E0 0 2E0 0 2 2 A 2 E0 m0
A
m0
x
m0 /
1
②在 x ( A, ) 区间内,即 (1, ) 区间内
发现振子的几率： e
1
2
d / e
0
2
d 16% 0
5)谐振子处于高激发态时 n 15
由5. E 11.线性谐振子能级：
1 0 2
1 En (n ) 0 , (n 0, 1, 2, 3, 2
)
12.线性谐振子能级性质：
1) 能级分立,且非简并 2) 能隙间距相等 3) 具有零点能,即基态能为非零:
1 E0 0 2
4) 零点能的实验证据： 温度趋于绝对零度时，散射光强趋于一个不为零的值 13.级数法得谐振子本征波函数解：
2 / 2
H ( )
待确定函数 H ( ) 须满足,对于 R, H ( ) 为有限
d 2H dH 2 ( 1) H 0 2 d d
10.采用级数法解方程9. 得：欲满足 的情况下 H ( ) 为有限值，必须
2n 1, (n 0,1, 2, )
3) [Q, P ]
[ x, p ] i
4) 5)
[a, a ] 1 [a, a a] a, [a , a a] a
p2 1 1 1 2 2 2 2 m0 x 0 ( P Q ) 0 (a a ) 6) H 2m 2 2 2
7)
dH n ( ) 2nH n 1 ( ) d
Hn1 ( ) 2 Hn ( ) 2nHn1 ( ) 0
曾量子力学题库（网用）（1）讲解
曾量⼦⼒学题库（⽹⽤）（1）讲解⼀、简述题：1. （1）试述Wien 公式、Rayleigh-Jeans 公式和Planck 公式在解释⿊体辐射能量密度随频率分布的问题上的差别2. （1）试给出原⼦的特征长度的数量级（以m 为单位）及可见光的波长范围（以?为单位）3. （1）试⽤Einstein 光量⼦假说解释光电效应4. （1）试简述Bohr 的量⼦理论5. （1）简述波尔-索末菲的量⼦化条件6. （1）试述de Broglie 物质波假设7. （2）写出态的叠加原理8. （2）在给定的状态中测量某⼀⼒学量可得⼀测值概率分布。
问在此状态中能否测得其它⼒学量的概率分布？试举例说明。
9. （2）在给定状态下测量某⼀⼒学量，能测量到什么程度？ 10.（2）按照波函数的统计解释，试给出波函数应满⾜的条件11.（2）假设⼀体系的基态波函数在全空间上都⼤于零，试解释是否存在某⼀激发态，该激发态在全空间范围内也都⼤于零。
12.（2）已知粒⼦波函数在球坐标中为),,(?θψr ，写出粒⼦在球壳),(dr r r +中被测到的⼏率以及在),(?θ⽅向的⽴体⾓元?θθΩd d d sin =中找到粒⼦的⼏率。
13.（2）什么是定态？它有哪些特征？ 14.（2）)()(x x δψ=是否定态？为什么？ 15.（2）设ikre r1=ψ，试写成其⼏率密度和⼏率流密度 16.（2）试解释为何微观粒⼦的状态可以⽤归⼀化的波函数完全描述。
17.（3）简述和解释隧道效应18.（3）⼀维⽆限深势阱体系??><∞≤≤=a x x a x x V or 000)(??><∞≤≤=ax x a x x V or 000)(处于状态 )(21)(ikx ikxe e ax --=ψ，其中a k π2=，请问该状态是否是定态？为什么？ 19.（3）说明⼀维⽅势阱体系中束缚态与共振态之间的联系与区别。
20.（3）某⼀维体系，粒⼦的势能为222x µγ，其中µ为粒⼦质量，说明该体系是什么体系，并写出体系能量的可能取值。
一维谐振子的 Schrodinger 方程的解及 Hermite 多项式的性质
z →−m
lim (z + m)Γ(z ) lim
(z + m)(z + m − 1) · · · (z + 1)Γ(z + 1) z →−m (z + m − 1) · · · (z + 1)z Γ(z + m + 1) = lim z →−m (z + m − 1) · · · (z + 1)z 1 = (−1)m m!
ξ →+ ∞
因而在这种情况下, 原 Schrödinger 方程无有界解. 现讨论 v 是非负整数的情况, 即 v = m, m 为非负整数. 在式 (23), (24)的基础上, 若 m 为偶数, 则式 y1 变为未定式, 而 y2 仍为原无界函数. 这时由递推式 (19), am+2 = 0, y1 为 m 次多项式；同样, 若 m 为奇数, 则 y1 为无界函数, y2 为 m 次多项式. 现研究 Γ 函数在 0 和负整数附近的性质. 由于 Res[Γ(z ), −m] = =
ξ2
(10) (11)
y ′′ − 2ξy ′ + (ν − 1)y = 0. 式 (11)即为 Hermite 微分方程.
2
2 Hermite 方程的幂级数求解
下面用幂级数法对 Hermite 方程进行求解. 重写 Hermite 方程如下, 在其中令 λ = ν − 1： y ′′ − 2ξy ′ + λy = 0. 设 y (ξ ) 为如下幂级数形式： y (ξ ) = 那么有 y
l
(39)
变换求和哑元, 令 k = l − i, 则 y1 =
l ∑ (−1)l−i 22l−2i l! i=0
(2l − 2i)!i!
lim (z + m)Γ(z ) lim
(z + m)(z + m − 1) · · · (z + 1)Γ(z + 1) z →−m (z + m − 1) · · · (z + 1)z Γ(z + m + 1) = lim z →−m (z + m − 1) · · · (z + 1)z 1 = (−1)m m!
ξ →+ ∞
因而在这种情况下, 原 Schrödinger 方程无有界解. 现讨论 v 是非负整数的情况, 即 v = m, m 为非负整数. 在式 (23), (24)的基础上, 若 m 为偶数, 则式 y1 变为未定式, 而 y2 仍为原无界函数. 这时由递推式 (19), am+2 = 0, y1 为 m 次多项式；同样, 若 m 为奇数, 则 y1 为无界函数, y2 为 m 次多项式. 现研究 Γ 函数在 0 和负整数附近的性质. 由于 Res[Γ(z ), −m] = =
ξ2
(10) (11)
y ′′ − 2ξy ′ + (ν − 1)y = 0. 式 (11)即为 Hermite 微分方程.
2
2 Hermite 方程的幂级数求解
下面用幂级数法对 Hermite 方程进行求解. 重写 Hermite 方程如下, 在其中令 λ = ν − 1： y ′′ − 2ξy ′ + λy = 0. 设 y (ξ ) 为如下幂级数形式： y (ξ ) = 那么有 y
l
(39)
变换求和哑元, 令 k = l − i, 则 y1 =
l ∑ (−1)l−i 22l−2i l! i=0
(2l − 2i)!i!
一维谐振子拉格朗日表达式
一维谐振子拉格朗日表达式（实用版）目录一、引言二、一维谐振子的定义和特点三、拉格朗日表达式的概念和作用四、一维谐振子的拉格朗日表达式五、结论正文一、引言在物理学中，一维谐振子是一个沿直线方向作简谐振动的物体。
它是研究简谐振动规律的基本模型，对于理解更复杂的振动系统具有重要意义。
拉格朗日表达式是分析一维谐振子运动的有效工具，可以帮助我们更好地描述和研究这种振动现象。
本文将从一维谐振子的定义和特点入手，介绍拉格朗日表达式的概念和作用，最后详细阐述一维谐振子的拉格朗日表达式。
二、一维谐振子的定义和特点一维谐振子是指在一个直线方向上作简谐振动的物体。
它的运动由一个势能函数 V(x) 描述，这个势能函数在一维空间上的图像是一个关于 x 的周期函数。
一维谐振子的运动特点是周期性的、振幅不变的、能量守恒的。
在运动过程中，物体的位移随时间作正弦或余弦函数变化，速度和加速度分别与位移成正比和反比关系。
三、拉格朗日表达式的概念和作用拉格朗日表达式是分析物体运动的一种数学表达式，它是基于拉格朗日力学原理推导得出的。
拉格朗日表达式包含了物体的运动方程和能量方程，可以描述物体在给定势能函数作用下的运动状态。
对于一维谐振子，拉格朗日表达式可以给出振动的周期、振幅、频率等物理量，为研究简谐振动提供理论依据。
四、一维谐振子的拉格朗日表达式对于一维谐振子，我们可以根据势能函数 V(x) 推导出拉格朗日表达式。
首先，根据拉格朗日力学原理，可以得到物体的运动方程：$$frac{dmathbf{}}{dt}frac{dmathbf{L}}{dq[1]}-frac{dmathbf{L }}{dq}=0$$其中，$mathbf{L}$表示拉格朗日量，$mathbf{q}$表示广义坐标，是时间 t 的函数，而$mathbf{q[1]}$表示广义速度。
在一维谐振子问题中，广义坐标和广义速度可以表示为：$$mathbf{q}=x,quad mathbf{q[1]}=dot{x}$$将上述广义坐标和广义速度代入运动方程，得到：$$frac{d}{dt}frac{d}{d{x}}mathbf{L}-frac{d}{d{x}}mathbf{L}= 0$$由于拉格朗日量$mathbf{L}$是物体的动能加上势能，对于一维谐振子，可以表示为：$$mathbf{L}=frac{1}{2}m{v}^{2}+V(x)$$其中，m 表示物体的质量，v 表示物体的速度。
周 一维谐振子问题
[bk2 (k 1)(k 2) 2kbk bk ( 1)] k 0
k
即： bk2 (k 1)(k 2) 2kbk bk ( 1)=0
该式对任意ξ都 成立，故ξ同次
从而导出系数 bk 的递推公式：
幂前的系数均应 为零，
bk 2
2k 1
(k 1)(k 2) bk
由上式可以看出：
a
x
0
V0
取新坐标原点为(a, V0)，则势可表示为 标准谐振子势的形式：
V(x)
V ( x) 1 kx2 2
a
x
0
V0
可见，一些复杂的势场下粒子的运动往往 可以用线性谐振动来近似描述。
在微观领域中，一维量子谐振子问题也是个基
本的问题，甚至更为基本。因为它不仅是微观粒 子在稳定平衡位置附近作小振动一类常见问题的 普遍概括，而且更是将来场量子化的基础。
(II) ξ→±∞ 需要考虑无穷级数的收敛性
b k2 k2 bk k
2k 1 2 (k 1)(k 2)
k
22 k
为此考察相邻 两项之比：
考察幂级数exp[
exp[ 2 ] 1 2
4
k
k2
展开式的收敛性
1! 2!
(
k 2
)!
(
k 2
1)!
比较二级数可知：
相继两项之比：
k2
V0
若取V0 = 0，即平衡位置处于势 V = 0 点，则
V 1 m2x2
2
量子力学中的线性谐振子就是指在该式所描述的势场中 运动的粒子。
（2）为什么研究线性谐振子
自然界广泛碰到简谐振动，任何体系在平 衡位置附近的小振动，
分子振动 晶格振动 原子核表面振动 辐射场的振动
一维谐振子零点能问题
（♥）
可证明，对谐振子的任何一个能量本征态 ψ n 有： * * ˆ ψ n ( x) d x = ∫ ψ n x = ∫ ψn ( x) x ( x ) xψ n ( x ) d x = 0 ∂ψ n ( x ) * * ˆ ψ n ( x ) d x = − ih ∫ ψ n ( x ) p = ∫ ψ n ( x) p dx=0
ˆ, p ˆx]≡ x ˆp ˆx − p ˆxx ˆ ≡ ih ˆ x 的对易关系 [ x ˆ 和 p 利用 x
可证明下面的对易关系：
ih 1 2 ˆ ˆ ˆ ˆ ˆx [ x, H ] = [ x, px ] = p m 2m ˆ ] = 1 k[ p ˆx,H ˆx, x ˆ 2 ] = − i h kx ˆ [p 2
1 ⎡ * ⎤ ˆ ψ ( x) d x − [H ˆ *ψ * ( x )] p ˆ ˆ ψ ( x ) p H ψ ( x ) d x = x n n x n ∫ ⎥ ⎦ ⎣∫ n − ihk ⎢
对谐振子的任何一个能量本征态 ψ n 有：
ˆ ψ ( x ) = E ψ ( x ), H n n n ˆ *ψ * ( x ) = [ H ˆ ψ ( x )]∗ = E ψ * ( x ) H n n n n
x = 0, p=0
（1）对易关系
ˆxx ˆ ψ = − ih p
∂ψ ∂ ˆp ˆ xψ ( xψ ) = − i h ψ + x ( − i h ) = − ih ψ + x ∂x ∂x
ˆp ˆx − p ˆxx ˆ )ψ = ihψ 对任意函数成立，所以： (x
ˆ x 的对易关系 ˆ, p ˆx]≡ x ˆp ˆx − p ˆxx ˆ ≡ ih 称为 x [x ˆ 和 p
一维谐振子基态和激发态的波函数
标题：深度探讨一维谐振子基态和激发态的波函数一、引言一维谐振子是量子力学中的经典问题之一，它的波函数描述了粒子在谐振势场中的运动状态。
在本文中，我们将深入探讨一维谐振子的基态和激发态的波函数，分析其数学形式和物理意义，以帮助读者更好地理解这一重要概念。
二、基态的波函数让我们来分析一维谐振子的基态波函数。
基态对应能量最低的状态，其波函数通常用Ψ₁(x)来表示。
在一维谐振子中，基态波函数可以用简单的数学形式进行描述：Ψ₁(x) = (mω/πħ)^(1/4) * e^(-mωx²/2ħ)其中，m是粒子的质量，ω是振子的角频率，ħ是约化普朗克常数。
这个波函数描述了基态下粒子在空间中的分布情况，通过对波函数的形式和特性进行分析，我们可以了解到粒子在基态下的基本运动状态和概率分布规律。
在基态下，粒子处于能量最低的状态，波函数的峰值对应着粒子最有可能出现的位置。
基态波函数的特性还可以通过数学手段进行分析，例如计算平均位置、动量期望值等，这些都能帮助我们更好地理解基态下粒子的运动规律和物理性质。
三、激发态的波函数接下来，我们将讨论一维谐振子的激发态波函数。
激发态对应能量高于基态的状态，其波函数通常用Ψ₂(x)来表示。
在一维谐振子中，激发态波函数的数学形式相对复杂一些，但通过分析和理解其特性，我们同样可以获得丰富的物理信息。
激发态波函数通常包含更多的波峰和波谷，描述了粒子在激发状态下的空间分布情况。
通过比较基态和激发态波函数的形式和特性，我们可以发现它们之间的微妙差别，并据此推断粒子在不同能级状态下的运动规律和行为。
激发态波函数的数学性质也具有重要意义，例如其振幅、波长、频率等特征参数都可以提供宝贵的信息。
通过对激发态波函数进行分析，我们可以更全面地理解粒子在谐振势场中的非基态运动状态，为进一步研究和应用提供重要的参考依据。
四、总结与展望通过本文的深度探讨，我们对一维谐振子的基态和激发态波函数有了全面的理解。
能量表象中的谐振子问题
( xn +1,n ) 2 − ( xn ,n −1 ) 2 =
ℏ
（14）
再利用式（4），即得
pn +1,n = iωµxn +1,n
(15)
x的矩阵元为实数，p的矩阵元为纯虚数，因此 的矩阵元为实数， 的矩阵元为纯虚数 的矩阵元为纯虚数， 的矩阵元为实数
xn ,n +1 = ( xn +1,n ) = xn +1,n
dA dt
H | ψ n 〉 = En | ψ n 〉 〈ψ n | H = En 〈ψ n |
dA = iωkn Akn dt kn
Ek − En = ℏωkn
其中 ω = ( E − E ) / ℏ kn k n
2.求和规则
∑ ( Ek − En ) xnk =
2 n
利用x的算符运动方程，可得
E = E0 , E0 + ℏω , E0 + 2ℏω.....
即
En = E0 + nℏω, n = 0,1,2......
(8)
为了求出基态能级，可以利用求和规则
∑ (E
n
n
− Ek ) | xnk |2 = ℏ / 2 µ
(9)
取k为基态（k=0），由式（6）（7）和 （9）可得
ℏ2 = ℏω ∑ | xn 0 |2 = ℏω ( x 2 )00 2µ n
在能量本征态|k>下求平均值，即得 iℏ = ( xpx )kk − ( px x )kk = ∑ xkn ( px )nk − ( px )kn xnk
n
= i µ ∑ (ωnk xkn xnk − ωkn xkn xnk ) = 2i µ ∑ ωnk xnk
16-4 一维谐振子问题
vx F I f 2 px 2 a me a '
2 2 2 ˆ 将算符 p x ( i ) 2 代入上式，得 x x
2 2 F me a x 2
ˆ A A ( r ) A ( r ) d
,
考虑一维谐振子的基态：
1 E 0 2 2 1 x
=
1 U ( x ) 2 x 2 2
——谐振子的特征长度
1 1
按照经典理论，
x , 经典允许区； x , 经典禁区.
按照量子力学中波函数的统计诠释，基态粒子处于经 典禁区中的概率为：
与 e 的渐进行为相同。
( ) 在 时将趋向无穷 若H ( ) 为无穷级数时， H ( ) 必 大。为了在 时，波函数仍有限， 须断为多项式。因为如果 H ( ) 是多项式，当
2
时，它趋于无穷的行为永远比 e
2 /2
趋于
零慢，从而保证了 ( ) 在 是有限。
粒子的动量的平均值：
i p
a ˆ dx p p 0
0
2 a nx d nx sin (i ) sin dx a 0 a dx a
在一维无限深方势阱中，粒子位置与动量的平均 值与粒子所处的本征态的级数，即 n 没有关系。 粒子的动能的平均值： 在势阱内部，势能为零，则粒子的动能也就是其总能 量。在定态问题中，总能量算符也就是哈密顿算符。
2 2
2k 2 22n2 En , n 1,2 ,3, 2 2 2 a
平均动能，即平均能量，是量子化的。
例4:求一维线性谐振子在第一激发态时概率最大的位 置。 解: 要求粒子在空间的概率的最大值，只要对概率密 度求极大即可。
在坐标表象中处理一维线性谐振子问题
在坐标表象中处理一维线性谐振子问题初中物理题目：在坐标表象中处理一维线性谐振子问题作者单位：响水滩乡中心学校作者姓名：宁国强2019年9月28日在坐标表象中处理一维线性谐振子问题响水滩中心学校宁国强摘要：本文阐述了在坐标表象中处理一维线性谐振子问题的方法和思路，阐述了一般表象的概念。
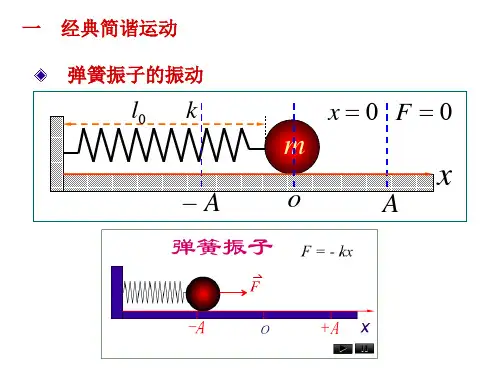
关键词：一维线性谐振子；坐标表象；一、能量本征值、本征函数的求解取自然平衡位置为坐标原点, 并选原点为势能零点, 则一维线性谐振子的势能为V (x ) =12μωx （1）22其中μ是谐振子的质量，ω是经典谐振子的自然频率。
一维谐振子的哈密顿函数为H =p22μ12μωx （2）22体系的能量本征方程（亦即不含时Schr ödinger 方程）为⎛ 2d 2122ˆ-+μωx 22⎛2μdx⎛⎛ψ⎛(x )=E ψ(x ) （3）严格的谐振子势是一个无限深势阱（如图1所示），粒子只存在束缚态，即起波函数应满足以下条件：ψ(x )−−→0 （4）x →∞将方程（3）无量纲化，为此，令2ξ==αx ，α=λ=2E ω（5）（3）式可改写为d ψd ξ+λ-ξ(2)ψ=0 （6）这是一个变系数二阶常微分方程。
为了求解它，我们先看ψ在ξ→±∞时的渐进行为。
当⎛⎛ξ⎛⎛很大时, λ与ξ2相比可以略去，因而在ξ→±∞ 时，方程(6)可近似表示为d ψd ξ22-ξψ=02 （7）±ξ/22它的渐近解为ψ~e ξ→±∞时，所以ψ e ξ2。
因为波函数的标准条件要求当ξ→±∞时ψ应为有限，2/2不满足边界条件(4)式，应弃之。
波函数指数上只能取负号，即ψ e -ξ/2。
方程(6)在ξ为有限处的根据以上讨论，可令方程(6)在ξ为有限处的解有如下形式：ψ(ξ)=A eξ22H (ξ) （8）式中A 为归一化系数，（8）代入(6)式，得d2H2d ξ-2ξd H（9）+(λ-1)H =0d ξ用级数解法，即把H 展开成ξ的幂级数来求这个方程的解。
一维谐振子的本征值问题.
一维谐振子的本征值问题姜罗罗赣南师范学院物理与电子信息科学系物理学专业2000级（2）班摘要：一维谐振子的本征值问题属于定态问题。
本文首先给出了一维谐振子本征值问题的Heisenberg 矩阵力学解法，Dirac算子代数解法和Schrödinger波动力学解法。
在此基础上，给出了一维半壁谐振子势阱（垒）问题的解法。
然后讨论了相干态和压缩态，它们是非经典量子效应，在超标准量子极限的高精度光学测量、超低噪光通信及量子通信领域有着广泛的应用前景，是物理学研究前沿课题之一。
最后从Dirac算子代数中求解出aˆ的本征态即谐振子的相干态，并由降算符aˆ与升算符+aˆ、光子数n与相位φ的最小不确定关系得出相干态和压缩态。
关键词：量子力学、一维谐振子、Heisenberg矩阵力学、算子代数解法、Schrödinger波动力学、一维半壁谐振子势阱（垒）、相干态、压缩态。
在量子力学中谐振子不仅是说明量子力学基本原理和方法的一个很好的例子，而且任何体系在平衡位置附近的小振动，例如:分子的振动，原子核辐射场及其他玻色场的振动等，在选择恰当的坐标后，常常可以分解为若干彼此独立的一维谐振子振动]1[.1925年Heisenberg发现矩阵力学，1926年Schrödinger创立波动力学，同时，Dirac创立在数学上更为一般的理论.可包括矩阵及波动两种形式]2[.一维谐振子的能力本征值问题，在历史上首先为Heisenberg的矩阵力学解决，后来用算子代数的方法给出了极漂亮的解，一般的教材只给定了波动力学的解法]3[.自1963年，Glauber ]4[等人提出谐振子相干态以后，相干态和压缩态以其特有的最小不确定性和超完备性备受人们的关注，被广泛应用于量子光学等领域]135[-。
一维谐振子的本征值问题属于定态问题。
本文首先给出了一维谐振子本征值问题的Heisenberg 矩阵力学解法，Dirac 算子代数解法和Schr ödinger 波动力学解法。
一维谐振子能级和波函数的代数解法
一维谐振子能级和波函数的代数解法上一回我们解出了粒子在一维无限深势阱中的波函数，这次我们将求解一维谐振子，也就是粒子在势能 V(x)=\frac{1}{2}m\omega^2x^2 下的波函数。
其中 m 为粒子质量， \omega 为振动的圆频率， x 为粒子的位置。
我们还是来研究定态薛定谔方程，将V(x)=\frac{1}{2}m\omega^2x^2 代入得到： -\frac{\hbar^2}{2m}\frac{\mathrm{d}^2\psi}{\mathrm{d}x^2}+\frac{1 }{2}m\omega^2x^2\psi=E\psi .一般来说，解决这样的方程需要用到多项式解，但这里我们先介绍一种代数解法，这可以省去很多计算。
对易子一维谐振子的哈密顿算符可以写成：\hat{H}=\frac{1}{2m}(\hat{p}^2+m^2\omega^2x^2) ，如果它可以“因式分解”的话，应该有： \hat{p}^2+m^2\omega^2x^2=[m^2\omega^2x^2-(i\hat{p})^2]=(i\hat{p}+m\omega x)(-i\hat{p}+m\omega x) .但事情远没有那么简单，此前我也告诉过你：算符之间是不能随意交换顺序的（类比矩阵乘法），因此那个“因式分解”不一定成立。
升降算符定义算符 \hat{a}_\pm=\frac{1}{\sqrt{2\hbar m\omega}}(\mpi\hat{p}+m\omega x) ，则由上面的推导我们有： 2\hbarm\omega(\hat{a}_-\hat{a}_+)=2m\hat{H}-im\omega[x,\hat{p}]=2m\hat{H}+\hbar m\omega ，则可以解得哈密顿算符为： \hat{H}=(\hat{a}_-\hat{a}_+-\frac{1}{2})\hbar\omega .我们发现，当算符 \hat{a}_+ 作用在 \psi(x) 上时，体系的能量会增加 \hbar\omega ，我们可以从定态薛定谔方程入手证明。
一维线性谐振子波函数及概率分布的可视演示
一维线性谐振子波函数及概率分布的可视演示
一维线性谐振子是量子力学中的经典问题之一，它的波函数和概率分布在物理学中有着重要的意义。
在本文中，我们将通过可视演示的方式，来展示一维线性谐振子的波函数及其概率分布。
一维线性谐振子是指在一维空间中，受到线性回复力作用的质点。
它的势能函数可以表示为V(x) = 0.5 * k * x^2，其中k为弹簧的弹性系数，x为质点与平衡位置的位移。
让我们来看一维线性谐振子的波函数是怎样的。
根据量子力学的定态方程，一维线性谐振子的波函数可以表示为：
Ψ(x) = A * exp(-0.5 * (m * ω * x^2 / ℏ)) * Hn(m * ω / ℏ)^0.5(x),
其中A为归一化系数，m为质点的质量，ω为振子的频率，ℏ为普朗克常数，Hn为厄米多项式。
通过对波函数的可视化，我们可以看到谐振子波函数在位移x方向上的变化规律，以及不同能级的波函数形态。
P(x) = |Ψ(x)|^2,
通过对概率分布的可视化，我们可以看到不同能级的概率分布形态，以及在不同位置上质点的出现概率。
这有助于我们更直观地理解一维线性谐振子在空间中的分布规律。
除了波函数和概率分布的可视化演示，我们还可以通过改变谐振子的参数（如弹簧的弹性系数、质点的质量、振子的频率等），来观察波函数和概率分布的变化规律。
这有助于我们更深入地理解一维线性谐振子的量子特性。
通过可视演示一维线性谐振子的波函数及其概率分布，我们可以更直观地理解量子力学中的经典问题，有助于我们在学习和研究中更好地理解和运用相关概念。
希望本文能对读者有所帮助，激发对量子力学的兴趣和深入探索。
一维谐振子拉格朗日表达式
一维谐振子拉格朗日表达式摘要：一、引言1.介绍一维谐振子的概念2.阐述研究一维谐振子的重要性二、一维谐振子的拉格朗日表达式1.拉格朗日表达式的基本概念2.一维谐振子的拉格朗日表达式的推导过程三、一维谐振子拉格朗日表达式的应用1.分析一维谐振子的运动状态2.探究一维谐振子的运动规律四、结论1.总结一维谐振子拉格朗日表达式的重要性2.展望一维谐振子拉格朗日表达式在未来的研究前景正文：一、引言在物理学的研究中，谐振子的概念及其运动规律一直是一个重要的研究对象。
谐振子是一个理想化的物理模型，它可以用来描述很多实际系统的振动现象。
一维谐振子是谐振子的一种特殊形式，它的运动仅在一个方向上进行。
研究一维谐振子，不仅有助于我们更深入地理解谐振子的基本性质，还可以为实际问题提供有用的理论指导。
二、一维谐振子的拉格朗日表达式1.拉格朗日表达式的基本概念在研究一维谐振子的运动规律时，我们通常会采用拉格朗日表达式的方法。
拉格朗日表达式是一种用来描述物体运动状态的数学表达式，它包含了物体的位置、速度和加速度等物理量。
通过求解拉格朗日表达式，我们可以得到物体在运动过程中的各种物理量，从而更好地理解其运动规律。
2.一维谐振子的拉格朗日表达式的推导过程一维谐振子的拉格朗日表达式可以通过以下步骤推导得到：首先，我们选取一个一维谐振子系统的质点为研究对象，并设定其质量为m，弹性系数为k。
然后，我们选取一个参考系，并定义该参考系的原点为质点的初始位置。
接下来，我们考虑质点在运动过程中所受到的外力。
对于一维谐振子来说，它所受到的外力主要有重力和弹性力。
重力可以表示为mg，其中g 为重力加速度；弹性力可以表示为-kx，其中x 为质点偏离平衡位置的位移。
在考虑了外力之后，我们就可以根据拉格朗日方程来推导一维谐振子的拉格朗日表达式。
根据拉格朗日方程，我们有：L = T - V其中，L 表示拉格朗日量，T 表示质点的动能，V 表示质点的势能。
16-4 一维谐振子问题
粒子的动量的平均值： 粒子的动量的平均值：
v − i h∇ ⇔ p
a v ∗ ˆ p = ∫ ψ pψdx
=0
2 a nπx d nπx = ∫ sin (−ih ) sin dx a 0 a dx a
0
在一维无限深方势阱中， 在一维无限深方势阱中，粒子位置与动量的平均 值与粒子所处的本征态的级数， 没有关系。 值与粒子所处的本征态的级数，即 n 没有关系。 粒子的动能的平均值： 粒子的动能的平均值： 在势阱内部，势能为零， 在势阱内部，势能为零，则粒子的动能也就是其总能 在定态问题中，总能量算符也就是哈密顿算符。 量。在定态问题中，总能量算符也就是哈密顿算符。
α=
µω
最简单的几个厄米多项式为： 最简单的几个厄米多项式为： n=0,
H 0 (ξ ) = 1,
n=1,
H 1 (ξ ) = 2ξ ,
− iEnt / h
n=2,
H 2 (ξ ) = 4ξ 2 − 2 ,
一维谐振子的波函数的一般形式为
ψ n ( x, t ) = ψ n ( x)e
= N ne
−α 2 x 2 2
————一维谐振子的定态薛定谔方程 一维谐振子的定态薛定谔方程 ————一维谐振子的能量本征值方程 一维谐振子的能量本征值方程
h2 d2 1 2 2 + µω x ψ ( x) = Eψ ( x) − 2 2 2 µ dx
为了简洁起见，引入三个无量纲参量： 为了简洁起见，引入三个无量纲参量：
a
2
πx dx a
=
2 πh 2 me a
3
∫0 sin
−7
π
me a3
= 1.17 × 10 N
试求： 例2:如果粒子的波函数为 ψ ( r , θ , ϕ ) ，试求： 如果粒子的波函数为 内找到粒子的概率； 在r到r+dr的球壳内找到粒子的概率； 到 的球壳内找到粒子的概率 要求概率，只要确定概率密度和相应的体积。 解: 要求概率，只要确定概率密度和相应的体积。 球坐标系下的体积元的表达式： 球坐标系下的体积元的表达式：
v − i h∇ ⇔ p
a v ∗ ˆ p = ∫ ψ pψdx
=0
2 a nπx d nπx = ∫ sin (−ih ) sin dx a 0 a dx a
0
在一维无限深方势阱中， 在一维无限深方势阱中，粒子位置与动量的平均 值与粒子所处的本征态的级数， 没有关系。 值与粒子所处的本征态的级数，即 n 没有关系。 粒子的动能的平均值： 粒子的动能的平均值： 在势阱内部，势能为零， 在势阱内部，势能为零，则粒子的动能也就是其总能 在定态问题中，总能量算符也就是哈密顿算符。 量。在定态问题中，总能量算符也就是哈密顿算符。
α=
µω
最简单的几个厄米多项式为： 最简单的几个厄米多项式为： n=0,
H 0 (ξ ) = 1,
n=1,
H 1 (ξ ) = 2ξ ,
− iEnt / h
n=2,
H 2 (ξ ) = 4ξ 2 − 2 ,
一维谐振子的波函数的一般形式为
ψ n ( x, t ) = ψ n ( x)e
= N ne
−α 2 x 2 2
————一维谐振子的定态薛定谔方程 一维谐振子的定态薛定谔方程 ————一维谐振子的能量本征值方程 一维谐振子的能量本征值方程
h2 d2 1 2 2 + µω x ψ ( x) = Eψ ( x) − 2 2 2 µ dx
为了简洁起见，引入三个无量纲参量： 为了简洁起见，引入三个无量纲参量：
a
2
πx dx a
=
2 πh 2 me a
3
∫0 sin
−7
π
me a3
= 1.17 × 10 N
试求： 例2:如果粒子的波函数为 ψ ( r , θ , ϕ ) ，试求： 如果粒子的波函数为 内找到粒子的概率； 在r到r+dr的球壳内找到粒子的概率； 到 的球壳内找到粒子的概率 要求概率，只要确定概率密度和相应的体积。 解: 要求概率，只要确定概率密度和相应的体积。 球坐标系下的体积元的表达式： 球坐标系下的体积元的表达式：
一维量子谐振子问题
ik2 a
x a,
2 (a) 3 (a) :
Be
ik2 a ik1a Be ce
(a) 3 (a) : 2 k 2 Be
由此可得
ik2 a
k2e
ik2 a
ika1
k1ce
ik1a
4 k1 k 2 e c A 2 ik2 a 2 ik2 a ( k1 k 2 ) e ( k1 k 2 ) e 2i (k1 k 2 ) sin k 2 a A A 2 ik2 a 2 ik2 a ( k1 k 2 ) e ( k1 k 2 ) e
可得
dx ,
. n 2 n!
Nn
2.讨论 1 E0 (1) 能级是等间隔的 ；(2)零点能是 ；(3)能级 2 n 的宇称偶奇相间，基态是偶宇称,即ψn(-x)=(-1)ψn(x) (4)ψn(x)有 n个节点。 四.几率分布:
在经典力学中,在ξ到ξ+dξ之间的区域内找到质点的
(3.2 7)
H 0 1, H 1 2 , H 2 4 2 2, H 3 8 3 12 , H 4 16 4 48 2 12, H 5 32 5 160 3 120 .
三. 线性谐振子的能级和波函数 1.我们把线性谐振子的能级和波函数总结如下。能级是：
现在H(ξ)的方程成为：
d 2Hn dHn 2 2nHn 0. 2 d d
而不难验证下面的函数正满足这个方程: n 2 d n 2 H n ( ) (1) e e . n d 它称为n次Hermitian多项式。 头五个Hermitian多项式是:
(3.2 6)
x a,
2 (a) 3 (a) :
Be
ik2 a ik1a Be ce
(a) 3 (a) : 2 k 2 Be
由此可得
ik2 a
k2e
ik2 a
ika1
k1ce
ik1a
4 k1 k 2 e c A 2 ik2 a 2 ik2 a ( k1 k 2 ) e ( k1 k 2 ) e 2i (k1 k 2 ) sin k 2 a A A 2 ik2 a 2 ik2 a ( k1 k 2 ) e ( k1 k 2 ) e
可得
dx ,
. n 2 n!
Nn
2.讨论 1 E0 (1) 能级是等间隔的 ；(2)零点能是 ；(3)能级 2 n 的宇称偶奇相间，基态是偶宇称,即ψn(-x)=(-1)ψn(x) (4)ψn(x)有 n个节点。 四.几率分布:
在经典力学中,在ξ到ξ+dξ之间的区域内找到质点的
(3.2 7)
H 0 1, H 1 2 , H 2 4 2 2, H 3 8 3 12 , H 4 16 4 48 2 12, H 5 32 5 160 3 120 .
三. 线性谐振子的能级和波函数 1.我们把线性谐振子的能级和波函数总结如下。能级是：
现在H(ξ)的方程成为：
d 2Hn dHn 2 2nHn 0. 2 d d
而不难验证下面的函数正满足这个方程: n 2 d n 2 H n ( ) (1) e e . n d 它称为n次Hermitian多项式。 头五个Hermitian多项式是:
(3.2 6)
量子力学中的一维谐振子问题求解
量子力学中的一维谐振子问题求解量子力学是研究微观粒子行为的一门学科，它描述了微观世界中的粒子的运动和相互作用。
谐振子是量子力学中一个经典的模型，它在多个领域中都有广泛的应用，如原子物理、固体物理和量子计算等。
在本文中，我们将探讨一维谐振子问题的求解方法。
一维谐振子是指一个质量为m的粒子在势能为V(x) = 1/2 kx²的势场中运动。
其中，k是弹性系数，x是粒子相对平衡位置的位移。
根据量子力学的原理，我们可以用薛定谔方程来描述一维谐振子的运动。
薛定谔方程是量子力学的基本方程，描述了粒子的波函数随时间的演化。
对于一维谐振子，薛定谔方程可以写成如下形式：Hψ(x) = Eψ(x)其中，H是哈密顿算符，定义为H = -ħ²/2m d²/dx² + 1/2 kx²。
ψ(x)是波函数，描述了粒子在不同位置的概率分布。
E是能量的本征值，对应于不同的能级。
为了求解一维谐振子的薛定谔方程，我们可以使用分离变量法。
假设波函数可以表示为ψ(x) = φ(x)χ(t)，其中φ(x)是位置的波函数，χ(t)是时间的波函数。
将这个形式代入薛定谔方程，可以得到两个方程：-ħ²/2m d²φ(x)/dx² + 1/2 kx²φ(x) = Eφ(x)iħ dχ(t)/dt = Etχ(t)第一个方程是一个关于位置的定态薛定谔方程，它描述了粒子在不同位置的运动。
第二个方程是一个关于时间的薛定谔方程，它描述了波函数随时间的演化。
对于定态薛定谔方程，我们可以使用数学方法求解。
一种常用的方法是使用升降算符。
升降算符是一对算符，可以将波函数的能级提升或降低一个单位。
对于一维谐振子，升降算符定义为a⁺ = (ħ/mω)^(1/2)(-d/dx + iωx)和a = (ħ/mω)^(1/2)(-d/dx - iωx)，其中ω = (k/m)^(1/2)是谐振子的频率。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电子与阱壁碰撞一次，电子所受到的冲量：
I ? ?? px?? px ? ?2px
电子与阱壁碰撞一次，阱壁所受到的冲量：
I ' ? ?I ? 2px
电子连续两次碰撞同一 侧阱壁所需要的时间：
T ? 2a vx
单位时间内电子碰撞同 一侧阱壁的次数：
f ? 1 ? vx T 2a
单位时间内电子对同一侧阱壁的冲量，即冲力为
求解此方程，并考虑到束缚态条件，就可以得到一 维谐振子的能量本征值和与其对应的本征波函数。
二、一维谐振子的本征函数和能量本征值
一维谐振子的定态薛定谔方程的解，即一维谐振
子的定态波函数为：
?
n (x) ?
N e?? 2 x2 n
2Hn (? x)
由波函数的归一化条件 所确定的常系数 Nn为：
Nn
?
(
2
2 x2 ???
?
(x) ?
E?
( x)
———— 一维谐振子的定态薛定谔方程 ———— 一维谐振子的能量本征值方程
??? ?
?2
2?
d2 dx2
?
1 ??
2
2 x2 ???
?
(x) ?
E?
( x)
为了简洁起见，引入三个无量纲参量：
? ? ? x,
??
??
,
?
? ? 2E ??
d 2? (? ) ? (? ? ? 2 )? (? ) ? 0 d? 2
x ? Acos(? t ? ? )
o
x
在微观领域中，一维量子谐振子问题也是个基本的 问题，甚至更为基本。因为它不仅是微观粒子 在稳定平 衡位置附近作小振动一类常见问题的普遍概括 ，而且更 是将来场量子化的基础。
一维谐振子在量子力学中是一个重要的物理模 型。例如研究分子的振动、晶格的振动、原子核表 面的振动以及辐射场的振动，等等。
我们认为，微观粒子所处的势场的形式仍然可以表达 为
U (x) ? 1 ?? 2x2
2
粒子受到的势不随时间变化，这是一个定态问题！
??? ?
?2
2?
?
2
? U (r?)???
?
(r?) ?
E?
(r?)
———— 定态薛定谔方程
U (x) ? 1 ?? 2 x2
2
??? ?
?2
2?
d2 dx2
?
1 ??
化过程就是简谐振动。
简谐振动物体受到的线性回复力 F ? ? kx
取系统的平衡位置作为系统势能的零点，简谐振动
系统的势能
U (x) ? 1 kx2 2
?? k ?
U (x) ? 1 ?? 2 x2
2
U (x)
简谐振动系统的总能量
U total
?
1 kA2 2
?
1 ??
2
2 A2
简谐振动运动方程的解
§16-4 一维谐振子问题
一、一维谐振子的定态薛定谔方程
在经典力学中，一维经典谐振子问题是个基本 的问题，它是物体在稳定平衡位置附近作小振动 这类常见问题的普遍概括。
在经典力学中，简谐振动的定义：
任何物理量 x 的变化规律若满足方程式
d2x dt 2
?
?
2x
?
0
并且 ω是决定于系统自身的常量，则该物理量的变
? n (x,t) ? ? n (x)e? iEnt/?
?
N e?? 2x2 n
2Hn (? x)e?iEnt / ? , n
?
0,1,2,3,...
一维谐振子的能量（本征值）为
E
?
En
?
(n ?
1)??
2
,
n ? 0,1,2,???
说明：
① 一维谐振子的能量只能取一系列 分立值；
En
?
?2k2
2?
? xe ? ? 2 x 2 / 2 ,
? ? ?
2 (x)
?
1
? 14
? 2? 2 x 2 ? 1 e , ?? 2 x2 / 2
2
考虑一维谐振子的基态：
= E0
?
1 2
??
U (x) ? 1 ?? 2 x2
2
x2 ? ?
??
? ?1 ?
?
——谐振子的特征长度
??
x ? ? ?1,经典允许区；
按照经典理论，
?
? 2?2n2
2? a 2
,
n ? 1,2,3,???
E?
En
?
(n ?
1)??
2
,
n ? 0,1,2,???
能量的分立现象在微观领域是普遍存在的！
② 一维谐振子的能谱是 等间距的，即相邻两能级的 能量差是固定的；
能级间距 = ??
③ 一维谐振子的基态能量不等于零，即存在零点能。
E0
?
1 2
??
零点能是微观粒子波粒 二象性的表现！
经典物理学中的一维谐振子：
U (x)
M
经典禁区
E
N
经典禁区
x ? A,经典允许区；
?A o
A x x ? A,经典禁区.
量子力学中的一维谐振子：? n ( x) ? Nn e? ? 2x2 2 H n (? x)
?
0 (x) ?
? ?14
e , ? ? 2 x2 / 2
? 1 (x) ?
2? ?14
F
?
I'f
?
2 px
vx 2a
?
px2 mea
将算符
p?x2
?
(? i?
?? )2 ??x
?
??2
?? ? ??x2
代入上式，得
F? ?
?
?2 me a
?2 ? x2
A ? A ? ?? ? (r?)A?? (r?)d?
一维无限深势阱的基态波函数为
? 1(x) ?
2 a
x ? ? ?1,经典禁区.
按照量子力学中波函数的统计诠释，基态粒子处于经
典禁区中的概率为：
? ? ?? ?1
?
??
? 0
(
x)?
0 (x)dx ?
??
?
? ?1
? 0
(
x)?
0 (x)dx
?
16%
——— 微观粒子的隧道效应
?
0 ( x)
?
? ?14
e , ? ? 2 x 2 / 2
? 1 ( x) ?
2? ?14
? xe ? ? 2 x 2 / 2 ,
? ? ?
2 ( x)
?
1
? 14
? 2? 2 x 2 ? 1 e ? ? 2 x2 / 2 ,
2
由图可以看出，量子数 n较小时，粒子位置的概率 密度分布与经典结论明显不同。随着量子数 n的增 大, 概率密度的平均分布将越来越接近于经典结论。
例1:一个电子被束缚在一维无限深势阱内，势阱宽度 为1.01? 10?10 m。求当电子处于基态时对阱壁的平均 冲力。 解: 要求平均冲力，先要求平均冲力算符。 设电子质量为 me、速度为 vx、动量为 px 、势阱宽度为 a。 平均冲力等于单位时间内的冲量。 动量定理：在运动过程中，作用于质点的合力在一段 时间内的冲量等于质点动量的增量。
?
1
?
2 2n
)1 n!
2
? ? ??
?
式中 Hn(? )称为厄米多项式 ，具体形式为
H n (?) ?
(?1) n e?2
dn
d? n
e -? 2
最简单的几个厄米多项式为：
n=0,
n=1,
n=2,
H 0 (?) ? 1,
H 1 (?) ? 2? ,
H 2 (?) ? 4? 2 ? 2 ,
一维谐振子的波函数的一般形式为
I ? ?? px?? px ? ?2px
电子与阱壁碰撞一次，阱壁所受到的冲量：
I ' ? ?I ? 2px
电子连续两次碰撞同一 侧阱壁所需要的时间：
T ? 2a vx
单位时间内电子碰撞同 一侧阱壁的次数：
f ? 1 ? vx T 2a
单位时间内电子对同一侧阱壁的冲量，即冲力为
求解此方程，并考虑到束缚态条件，就可以得到一 维谐振子的能量本征值和与其对应的本征波函数。
二、一维谐振子的本征函数和能量本征值
一维谐振子的定态薛定谔方程的解，即一维谐振
子的定态波函数为：
?
n (x) ?
N e?? 2 x2 n
2Hn (? x)
由波函数的归一化条件 所确定的常系数 Nn为：
Nn
?
(
2
2 x2 ???
?
(x) ?
E?
( x)
———— 一维谐振子的定态薛定谔方程 ———— 一维谐振子的能量本征值方程
??? ?
?2
2?
d2 dx2
?
1 ??
2
2 x2 ???
?
(x) ?
E?
( x)
为了简洁起见，引入三个无量纲参量：
? ? ? x,
??
??
,
?
? ? 2E ??
d 2? (? ) ? (? ? ? 2 )? (? ) ? 0 d? 2
x ? Acos(? t ? ? )
o
x
在微观领域中，一维量子谐振子问题也是个基本的 问题，甚至更为基本。因为它不仅是微观粒子 在稳定平 衡位置附近作小振动一类常见问题的普遍概括 ，而且更 是将来场量子化的基础。
一维谐振子在量子力学中是一个重要的物理模 型。例如研究分子的振动、晶格的振动、原子核表 面的振动以及辐射场的振动，等等。
我们认为，微观粒子所处的势场的形式仍然可以表达 为
U (x) ? 1 ?? 2x2
2
粒子受到的势不随时间变化，这是一个定态问题！
??? ?
?2
2?
?
2
? U (r?)???
?
(r?) ?
E?
(r?)
———— 定态薛定谔方程
U (x) ? 1 ?? 2 x2
2
??? ?
?2
2?
d2 dx2
?
1 ??
化过程就是简谐振动。
简谐振动物体受到的线性回复力 F ? ? kx
取系统的平衡位置作为系统势能的零点，简谐振动
系统的势能
U (x) ? 1 kx2 2
?? k ?
U (x) ? 1 ?? 2 x2
2
U (x)
简谐振动系统的总能量
U total
?
1 kA2 2
?
1 ??
2
2 A2
简谐振动运动方程的解
§16-4 一维谐振子问题
一、一维谐振子的定态薛定谔方程
在经典力学中，一维经典谐振子问题是个基本 的问题，它是物体在稳定平衡位置附近作小振动 这类常见问题的普遍概括。
在经典力学中，简谐振动的定义：
任何物理量 x 的变化规律若满足方程式
d2x dt 2
?
?
2x
?
0
并且 ω是决定于系统自身的常量，则该物理量的变
? n (x,t) ? ? n (x)e? iEnt/?
?
N e?? 2x2 n
2Hn (? x)e?iEnt / ? , n
?
0,1,2,3,...
一维谐振子的能量（本征值）为
E
?
En
?
(n ?
1)??
2
,
n ? 0,1,2,???
说明：
① 一维谐振子的能量只能取一系列 分立值；
En
?
?2k2
2?
? xe ? ? 2 x 2 / 2 ,
? ? ?
2 (x)
?
1
? 14
? 2? 2 x 2 ? 1 e , ?? 2 x2 / 2
2
考虑一维谐振子的基态：
= E0
?
1 2
??
U (x) ? 1 ?? 2 x2
2
x2 ? ?
??
? ?1 ?
?
——谐振子的特征长度
??
x ? ? ?1,经典允许区；
按照经典理论，
?
? 2?2n2
2? a 2
,
n ? 1,2,3,???
E?
En
?
(n ?
1)??
2
,
n ? 0,1,2,???
能量的分立现象在微观领域是普遍存在的！
② 一维谐振子的能谱是 等间距的，即相邻两能级的 能量差是固定的；
能级间距 = ??
③ 一维谐振子的基态能量不等于零，即存在零点能。
E0
?
1 2
??
零点能是微观粒子波粒 二象性的表现！
经典物理学中的一维谐振子：
U (x)
M
经典禁区
E
N
经典禁区
x ? A,经典允许区；
?A o
A x x ? A,经典禁区.
量子力学中的一维谐振子：? n ( x) ? Nn e? ? 2x2 2 H n (? x)
?
0 (x) ?
? ?14
e , ? ? 2 x2 / 2
? 1 (x) ?
2? ?14
F
?
I'f
?
2 px
vx 2a
?
px2 mea
将算符
p?x2
?
(? i?
?? )2 ??x
?
??2
?? ? ??x2
代入上式，得
F? ?
?
?2 me a
?2 ? x2
A ? A ? ?? ? (r?)A?? (r?)d?
一维无限深势阱的基态波函数为
? 1(x) ?
2 a
x ? ? ?1,经典禁区.
按照量子力学中波函数的统计诠释，基态粒子处于经
典禁区中的概率为：
? ? ?? ?1
?
??
? 0
(
x)?
0 (x)dx ?
??
?
? ?1
? 0
(
x)?
0 (x)dx
?
16%
——— 微观粒子的隧道效应
?
0 ( x)
?
? ?14
e , ? ? 2 x 2 / 2
? 1 ( x) ?
2? ?14
? xe ? ? 2 x 2 / 2 ,
? ? ?
2 ( x)
?
1
? 14
? 2? 2 x 2 ? 1 e ? ? 2 x2 / 2 ,
2
由图可以看出，量子数 n较小时，粒子位置的概率 密度分布与经典结论明显不同。随着量子数 n的增 大, 概率密度的平均分布将越来越接近于经典结论。
例1:一个电子被束缚在一维无限深势阱内，势阱宽度 为1.01? 10?10 m。求当电子处于基态时对阱壁的平均 冲力。 解: 要求平均冲力，先要求平均冲力算符。 设电子质量为 me、速度为 vx、动量为 px 、势阱宽度为 a。 平均冲力等于单位时间内的冲量。 动量定理：在运动过程中，作用于质点的合力在一段 时间内的冲量等于质点动量的增量。
?
1
?
2 2n
)1 n!
2
? ? ??
?
式中 Hn(? )称为厄米多项式 ，具体形式为
H n (?) ?
(?1) n e?2
dn
d? n
e -? 2
最简单的几个厄米多项式为：
n=0,
n=1,
n=2,
H 0 (?) ? 1,
H 1 (?) ? 2? ,
H 2 (?) ? 4? 2 ? 2 ,
一维谐振子的波函数的一般形式为