下载文档原格式
量子隧穿效应量子隧穿效应是量子力学中一种重要且奇特的现象，它描述的是微观粒子在类似势垒的区域内，可能出现超越经典物理学预测的穿越现象。
本文将介绍量子隧穿效应的基本原理、相关应用以及对科学发展的意义。
一、基本原理量子隧穿效应是基于量子力学的概念，其核心是波粒二象性原理。
根据波粒二象性，微观粒子既可以被看作波动，也可以被看作粒子。
在经典物理学中，一个粒子如果没有足够的能量，是无法通过势垒的，而必须越过该势垒才能继续前进。
然而，在量子力学中，微观粒子具有波动特性，它们在经过势垒时，会表现出概率波函数的干涉和叠加效应。
当概率波函数的幅度分布在势垒之外时，存在一定概率粒子会穿越势垒，进入本该被禁止的区域。
这种现象就是量子隧穿效应。
二、相关应用1. 扫描隧道显微镜扫描隧道显微镜（Scanning Tunneling Microscope，STM）是一种利用量子隧穿效应测量物体表面形貌和电子特性的高分辨率显微镜。
STM通过在探针和样品之间施加微小的电压，使电子通过隧穿效应从探针穿过空隙输送到样品表面上，通过对隧穿电流的测量得到样品表面的显微图像。
2. 四面体结构在化学领域，量子隧穿效应对于描述四面体结构的成键和反映分子之间的空间取向关系起着重要作用。
在传统化学中，四面体结构的成键被认为需要获得足够的能量，但隧道效应表明成键发生的可能性并不取决于能量，而是取决于波函数的幅度分布。
这一发现对于理解分子的结构和化学反应具有重大意义。
3. 穿隧发光二极管穿隧发光二极管（Tunneling Light Emitting Diode，TLED）是一种利用量子隧穿现象产生光辐射的新型光电器件。
TLED中的电子通过量子隧穿效应从导层穿越势垒进入禁带，使空穴和电子发生复合，释放能量并辐射光子。
TLED具有高效率、长寿命和低功耗等优点，具有广泛的应用前景。
三、科学意义量子隧穿效应的发现和研究突破了经典物理学的局限，揭示了微观世界的奇妙规律，对于拓展科学认知、推动科学发展具有重要意义。
隧道效应及其应用隧道效应是指电荷穿过微小通道时，隧道效应波在均匀媒质中传播，并在微小距离内消失，也就是说，将一种粒子注入到一个势垒中时，隧道效应将允许这种粒子到过势垒。
在材料科学技术中，隧道效应有着广泛的应用。
例如，金属-绝缘体-金属隧道结是一种重要的电子器件。
它在纳米电子学、超导电子学、晶体管和以太网协议等多种领域得到广泛应用。
本文将探讨隧道效应的相关知识和其应用。
一、隧道效应的基础知识隧道效应是一种量子力学现象，是发生在纳米尺度下的粒子动力学现象。
在典型的隧道效应过程中，电子“透过”屏障，而非越过屏障。
隧道效应中的关键因素是隧道势垒的高度和宽度，这是隧道效应发生的必要条件。
隧道效应是由卡尔·波普尔（Karl Popper）首先提出的，通过用微波照射大约10mm范围内的铍结构，波普尔和一组研究人员成功地验证了隧道效应假说。
事实上，隧道效应已经成为科学研究的基础，作为微电子器件的设计和制造过程中重要的一环。
二、金属-绝缘体-金属隧道结的应用金属-绝缘体-金属（MIM）隧道结是一种电子器件，其制备工艺为将绝缘层夹在两层金属层之间。
这种器件的应用可追溯到20世纪70年代，当时Dr. James Francis Gibbons将其应用于元越隧道效应（ESD）测量。
十年后，MIM隧道结被首次用于超导磁通量量子位的变化探测器。
现在，MIM隧道结被广泛运用于各种电子器件，包括晶体管、存储器、逻辑门和模拟单元。
这些器件源自于MIM隧道结具有优秀的诸如电流电压特性和噪声特性的性质。
三、隧道效应在半导体行业的应用半导体行业中，隧道效应在器件的制造和测试过程中具有重要的作用。
隧道效应被用作某些器件的基础结构，这些器件包括MOSFET、BIT、TET和BJT等。
在制造这些器件时，隧道效应被用作材料特性的测定和校准。
此外，隧道效应还被用于各种类型的测量，包括光子计数、电子自旋共振（ESR）、电子电感（ELI）测量等。
隧道（Josephson）效应及其应用Josephson 效应josephson 效应 即 隧道效应 。
隧道效应由微观粒子波动性所确定的量子效应。
又称势垒贯穿。
考虑粒子运动遇到一个高于粒子能量的势垒，按照经典力学，粒子是不可能越过势垒的；按照量子力学可以解出除了在势垒处的反射外，还有透过势垒的波函数，这表明在势垒的另一边，粒子具有一定的概率，粒子贯穿势垒。
约瑟夫森效应属于遂穿效应，但有别于一般的隧道效应，它是库伯电子对通过由超导体间通过若连接形成约瑟夫森结的超流效应。
历史沿革1957年，江崎玲於奈在改良高频晶体管2T7的过程中发现，当增加PN 结两端的电压时，电流反而减少，他将这种现象解释为隧道效应。
1960年，美裔挪威籍科学家加埃沃通过实验证明了在超导体隧道结中存在单电子隧道效应。
1962年，英国剑桥大学实验物理学研究生约瑟夫森预言，当两个超导体之间设置一个绝缘薄层构成SIS 时，电子可以穿过绝缘体从一个超导体到达另一个超导体。
这一预言不久就为P.W.安德森和J.M.罗厄耳的实验观测所证实——电子对通过两块超导金属间的薄绝缘层（厚度约为10埃）时发生了隧道效应，于是称之为“约瑟夫森效应”。
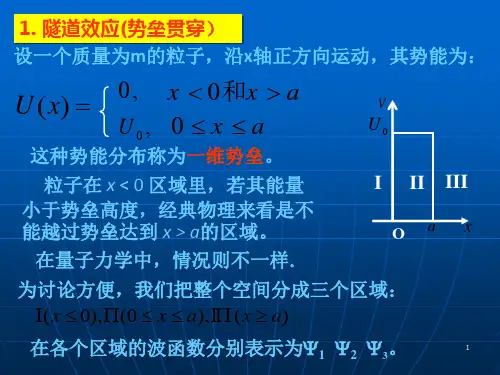
隧道效应(势垒贯穿）设一个质量为m 的粒子，沿x 轴正方向运动，其势能为：这种势能分布称为一维势垒。
粒子在 x < 0 区域里，若其能量小于势垒高度，经典物理来看是不能越过势垒 达到 x > a 的区域。
在量子力学中，情况则不一样。
为讨论方便，我们把整个空间分成三个区域：在各个区域的波函数分别表示为Ψ1 Ψ2 Ψ3 。
=)(x U ,0,0U ax x ><和0ax ≤≤00U VOa IIIxIII)(),0(),0(a x a x x ≥I∏≤≤∏≤I ),()(212122x E dxx d m ϕϕ=- 0≤x三个区间的薛定谔方程简化为：方程的通解为：三式的右边第一项表示沿x 方向传播的平面波，第二项为沿x 负方向传播的平面波。
穿墙而过不是梦！——神奇的量子隧道效应波粒二象性使微观粒子表现出许多在宏观世界里看起来不可思议的现象，隧道效应就是其中之一。
崂山道士的故事被我们当作笑话来看，但是，在量子世界里，因为有隧道效应，穿墙而过不再是什么难事，很容易就能做到。
借助隧道效应，人们发明了扫描隧道显微镜，不但“看见”了一个个原子，而且实现了移动、操控原子的梦想。
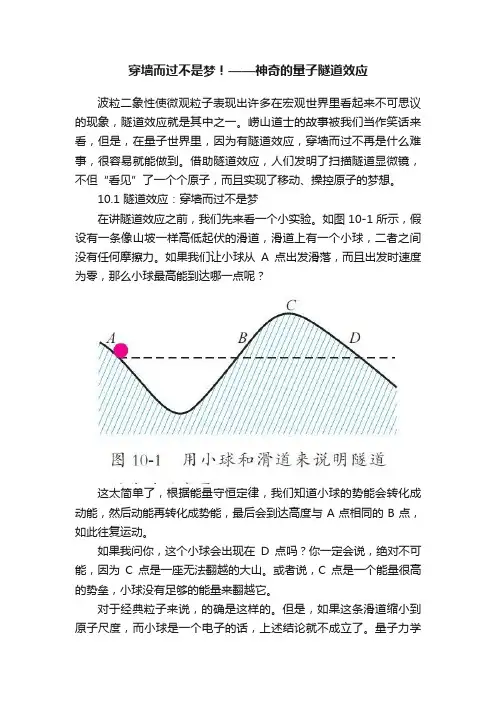
10.1 隧道效应：穿墙而过不是梦在讲隧道效应之前，我们先来看一个小实验。
如图10-1所示，假设有一条像山坡一样高低起伏的滑道，滑道上有一个小球，二者之间没有任何摩擦力。
如果我们让小球从A点出发滑落，而且出发时速度为零，那么小球最高能到达哪一点呢？这太简单了，根据能量守恒定律，我们知道小球的势能会转化成动能，然后动能再转化成势能，最后会到达高度与A点相同的B点，如此往复运动。
如果我问你，这个小球会出现在D点吗？你一定会说，绝对不可能，因为C点是一座无法翻越的大山。
或者说，C点是一个能量很高的势垒，小球没有足够的能量来翻越它。
对于经典粒子来说，的确是这样的。
但是，如果这条滑道缩小到原子尺度，而小球是一个电子的话，上述结论就不成立了。
量子力学计算表明，从A 点出发的电子有明显地出现在D 点的概率，就像是从一条隧道中穿越过去的一样，这就是量子隧道效应，它是微观粒子波粒二象性的体现。
总结一下，如果微观粒子遇到一个能量势垒，即使粒子的能量小于势垒高度，它也有一定的概率穿越势垒，这种现象就叫隧道效应。
隧道效应又称势垒贯穿，是一种很常见的量子效应。
也就是说，崂山道士的故事在量子世界里是很平常的，一点都不稀奇。
当然，对于不同的情况，粒子在势垒外出现的概率大小是需要通过薛定谔方程仔细计算的。
在一般情况下，只有当势垒宽度与微观粒子的德布罗意波长可比拟时，势垒贯穿的现象才能被显著观察到。
如果势垒太高或太宽，隧穿的可能性就会变得很小。
用量子隧道效应能部分地解释放射性元素的α 衰变现象。
α 衰变是从原子核中发射出α 粒子（氦原子核）的一种放射性现象。
隧道电阻效应隧道电阻效应是指在一些特定条件下，电子可以通过隧道效应穿越势垒，从而在两个电子能级之间形成电流。
这一现象是量子力学的基本原理之一，对于电子器件的设计和制造具有重要意义。
隧道电阻效应的发现可以追溯到20世纪50年代初，当时物理学家通过实验证实了电子可以在绝缘体-绝缘体结构中进行隧道穿越。
后来，随着技术的发展，人们发现隧道电阻效应不仅仅存在于绝缘体-绝缘体结构中，还可以在金属-绝缘体和金属-金属结构中观察到。
隧道电阻效应的产生与量子力学中的波粒二象性密切相关。
根据波粒二象性理论，电子既可以被看作是粒子，也可以被看作是波动。
当电子穿过势垒时，其波函数在势垒两侧都存在，虽然在势垒内的波函数幅值较小，但不为零。
根据波粒二象性理论，电子存在于势垒两侧的概率是非零的，从而电子有一定的概率可以穿越势垒，形成电流。
隧道电阻效应的大小与势垒的高度和宽度有关。
势垒越高，电子穿越的难度越大，电流越小；势垒越宽，电子穿越的难度越大，电流越小。
此外，电子的质量和能量也会影响隧道电阻效应的大小。
电子质量越大，电子穿越的难度越大，电流越小；电子能量越高，电子穿越的难度越小，电流越大。
隧道电阻效应在实际应用中有着广泛的应用。
例如，在隧道二极管中，由于隧道电阻效应的存在，电流可以通过绝缘层，从而实现高速电子输运。
这使得隧道二极管成为高速电子器件中的重要组成部分。
此外，隧道电阻效应还可以用于数据存储和传输，如隧道磁阻效应被应用于磁存储器中。
尽管隧道电阻效应在电子器件设计中起着重要作用，但它也存在一些限制。
首先，隧道电阻效应只在非常薄的绝缘层中才能观察到，因此制造过程对绝缘层的控制非常关键。
其次，隧道电阻效应会导致电子的能量损失，从而产生热量。
这对于一些高功率应用来说是一个不可忽视的问题。
隧道电阻效应是一种基于量子力学原理的现象，通过电子在势垒中的隧道穿越形成电流。
隧道电阻效应在电子器件设计和制造中起着重要作用，并在高速电子器件和数据存储中得到广泛应用。
《双势垒抛物量子阱结构中的电子隧穿》篇一一、引言量子力学是物理学中一个重要的分支，它研究微观领域内粒子的运动规律。
在固体物理中，电子的隧穿效应是一个重要的物理现象，它涉及到电子在势垒之间的传输和能量转换。
本文将探讨双势垒抛物量子阱结构中的电子隧穿现象，分析其基本原理和影响因素，并讨论其在电子器件中的应用。
二、双势垒抛物量子阱结构双势垒抛物量子阱结构是一种特殊的电子结构，由两个高势垒和中间的量子阱组成。
这种结构可以有效地限制电子的运动，使其在量子阱内进行量子态的跃迁和传输。
抛物线形状的势垒使得电子在传输过程中受到的力更加均匀，有利于提高电子隧穿的效率和稳定性。
三、电子隧穿基本原理电子隧穿是指电子在势垒的作用下，穿过势垒从一边到达另一边的过程。
这个过程可以用量子力学的波函数来描述。
在双势垒抛物量子阱结构中，电子隧穿的过程受到势垒高度、势垒宽度、量子阱深度和宽度等因素的影响。
当电子的能量低于势垒高度时，电子无法直接穿过势垒，而会在势垒两侧形成概率波函数，通过隧道效应穿过势垒。
四、影响电子隧穿的因素1. 势垒高度和宽度：势垒的高度和宽度对电子隧穿的影响非常大。
当势垒高度越高、宽度越宽时，电子穿过势垒的难度越大，隧穿几率越小。
反之，当势垒高度较低、宽度较窄时，电子更容易穿过势垒。
2. 量子阱深度和宽度：量子阱的深度和宽度也会影响电子隧穿的效果。
当量子阱深度较大时，可以更好地限制电子的运动，提高电子隧穿的效率。
而量子阱的宽度则影响着电子在量子阱内的传输距离和传输速度。
3. 电子能量：电子的能量是决定其能否穿过势垒的关键因素。
当电子的能量高于势垒高度时，电子可以直接穿过势垒；而当电子的能量低于势垒高度时，则需要通过隧道效应穿过势垒。
五、双势垒抛物量子阱结构中的应用双势垒抛物量子阱结构在电子器件中有着广泛的应用。
例如，在半导体器件中，可以利用双势垒抛物量子阱结构制备高效率的发光二极管、激光器等光电器件。
此外，还可以利用双势垒抛物量子阱结构制备高灵敏度的传感器、高效的太阳能电池等。
双抛物线势场中的隧道效应王 鑫(陕西理工学院 物理系2007级物理学3 班 ，陕西 汉中 723000)指导老师：王剑华[摘要]量子力学中的隧道效应是一种重要的物理现象，有着非常广泛的应用. 本文从薜定谔方程出发,讨论了求解双抛物线势场中的隧道效应，给出了相应的透射系数和反射系数，并对其进行讨论，研究其应用。
[关键词] 薜定谔方程与遂道效应；双抛物线势场中粒子的透射系数；双抛物线势场中粒子的透射系数；隧道效应及其应用引言在量子力学发展初期，德布罗意根据光的波粒二象性，提出了物质波假说，即认为微观粒子（电子、质子、中子等）也具有波动性。
由于微观粒子具有波动性因而它在能量E 小于势垒高度时仍能贯穿势垒，这种现象称为隧道效应，隧道效应完全是由于微观粒子具有波动的性质而来的。
1957年，江崎制成了隧道二极管，第一次令人信服地证实了固体中的电子隧道效应的存在。
1960年贾埃弗利用隧道效应测量了超导能隙，验证了超导理论。
1982年德国的宾尼等研制成功第一台扫描隧道显微镜，把隧道效应的应用推向一个新的阶段。
近几年来，人们十分关注分子和半导体量子阱中双势的隧道效应问题研究[4-8]，氨分子作为一个典型的三角锥形模型，早在1927年Hund 就提出量子隧道效应会对三角锥形分子的内部结构有很大的调整作用[1]。
适当选择外部条件便可在不同程度上控制分子结构的稳定性。
近几年来在介观尺度的隧道效应和光子隧道效应方面的研究日益成为热点[1-9]，如在超导技术及纳米技术方面的应用发展较为明显[3]。
本文就双抛物线的隧道效应问题求解并进行讨论[2-3]。
1 薛定谔方程与隧道效应在量子力学中，微观体系的运动状态是用一个波函数来描写的，反映微观粒子运动规律的微分方程是()t r ,ψ对时间的一阶微分方程，即:ψ+ψ∇-=∂ψ∂)(222r U t i μ(1.1) 我们称它为薛定谔方程（Schrödinger equation)，式中)r (U是表征力场的函数。
量子与统计物理课题论文论文名称：量子力学中隧穿效应的原理及其应用所在班级：材料物理081小组成员：黄树繁（08920107）蒋昌达（08920108）摘要：量子隧穿效应为一种量子特性，是如电子等微观粒子能够穿过它们本来无法通过的“墙壁”的现象。
这是一种特殊的现象，这是因为根据量子力学，微观粒子具有波的性质，而有不为零的几率穿过位势障壁。
本文主要介绍量子隧穿效应的基本原理、简单和稍微复杂一点的情况的推导过程，然后介绍下隧穿效应在实际中的应用—扫描隧道显微镜（STM）。
关键词：量子力学；隧穿效应；STMAbstract:Tnneling effect is a property of quantum,is a effect of Microscopic particles ,for example electrons,can get through “barriers” which they cannot used to.It is a unique phenomenon in Quantum mechanics which do not exist in classical mechanics. This paper mainly introduce the basic principle of QM,and conduct the mathematical derivation of the modle. Finally,we introduce an important application in practice of quantum tunneling effect—Scanning Tunneling Microscope.Key Word: Quantum mechanics;Tunneling effect;STM0.引言对于一个经典粒子(具有一定的有效质量)在外加电磁场中的行为服从牛顿力学，同时还受到声子、杂质等的散射，无须考虑量子效应 ( 尺寸引起的量子化、量子力学隧穿透效应、量子相干效应等)。
隧道效应及其在电子学中的应用隧道效应是一种奇特的量子力学现象，它在电子学领域中发挥着重要作用。
本文将介绍隧道效应的基本原理以及它在电子学中的应用。
一、隧道效应的基本原理隧道效应是指当粒子穿过高能势垒时，虽然根据经典物理学的观点，粒子的能量不足以克服势垒，但量子力学的隧道效应却使粒子在没有足够能量的情况下穿越势垒。
这一现象的发生是由于当粒子接近势垒时，其波函数逐渐渗透到势垒内，并在势垒内部存在一定的概率，最终使得粒子穿越势垒。
隧道效应的发生需要满足几个条件。
首先，粒子的波长要比势垒宽度大得多，以保证波函数能够渗透到势垒内。
其次，势垒高度不能过高，否则粒子将无法穿越。
最后，温度要足够低，以保证粒子的能量较低。
二、隧道效应在电子学中的应用1. 隧道二极管隧道二极管是利用隧道效应制造的一种特殊二极管。
由于隧道效应的存在，电子能够在势垒中的能带间穿越，从而在电子能谱中形成一片隧道能带。
利用这个特性，隧道二极管可以实现低电压下的高速开关特性，因此被广泛应用于超高速电路、低功耗电路等领域。
2. 隧道场效应晶体管隧道场效应晶体管（TFET）是一种基于隧道效应的新型固态器件。
传统的场效应晶体管通过载流子在沟道中的迁移来实现导通，而TFET利用隧道效应实现载流子的输运和控制。
由于隧道效应的存在，TFET具有较低的开启电压和较小的漏电流，因此具有很好的低功耗特性。
TFET在集成电路中的应用前景广阔，可望替代传统MOSFET，实现更低功耗的电子器件。
3. 隧道磁阻元件隧道磁阻元件是一种利用隧道效应来检测磁场变化的器件。
它由两个磁性层夹持着一层绝缘层构成。
当外部磁场作用于器件时，磁性层的磁化方向发生变化，导致在绝缘层中形成隧道效应。
通过测量隧道电阻的变化，可以间接检测到外部磁场的变化。
隧道磁阻元件具有灵敏度高、响应速度快等优点，广泛应用于传感器、磁存储器等领域。
结语：隧道效应作为量子世界的奇妙现象，在电子学中的应用得到了广泛研究和开发。
量子隧穿效应及其应用量子隧穿效应是量子力学中的一个重要现象，它描述了微观粒子在经典力学中无法实现的穿越势垒的行为。
在经典物理学中，当一个粒子遇到一个高于其能量的势垒时，它将被完全反射。
然而，在量子力学中，粒子具有波粒二象性，因此存在一定的概率穿越势垒，即量子隧穿效应。
量子隧穿效应的基本原理是根据海森堡不确定性原理，粒子的位置和动量不能同时确定。
当粒子遇到势垒时，其位置被限制在势垒内，但其动量可以超过势垒所允许的范围。
因此，即使粒子的能量低于势垒的高度，它仍有一定的概率穿越势垒。
量子隧穿效应在许多领域都有重要的应用。
以下将介绍几个典型的应用。
1. 扫描隧道显微镜扫描隧道显微镜（Scanning Tunneling Microscope，STM）是一种利用量子隧穿效应来观察物质表面的仪器。
STM通过在样品表面和探针之间施加电压，利用量子隧穿电流来测量样品表面的形貌和电子结构。
由于量子隧穿效应的存在，STM可以实现纳米级别的分辨率，成为研究表面物理和纳米科学的重要工具。
2. 核聚变反应核聚变是一种将轻元素聚变成重元素的核反应。
在核聚变反应中，两个原子核需要克服库仑斥力才能靠近，这需要克服一个势垒。
量子隧穿效应可以提供一种额外的机制，使得原子核能够穿越势垒，从而增加核聚变反应的概率。
因此，量子隧穿效应在核聚变反应中起到了重要的作用。
3. 量子隧穿二极管量子隧穿二极管是一种基于量子隧穿效应的电子器件。
它利用了电子在势垒中的量子隧穿现象，实现了电流在势垒中的穿越。
量子隧穿二极管具有低电压驱动、高速响应和低功耗等优点，被广泛应用于高速电子器件和量子计算领域。
4. 量子隧穿复合量子隧穿复合是一种利用量子隧穿效应实现电子和空穴的复合的技术。
在半导体材料中，电子和空穴可以通过量子隧穿效应穿越势垒，从而在势垒的另一侧发生复合。
量子隧穿复合技术可以用于制备高效率的光电器件，如太阳能电池和光电探测器。
总结起来，量子隧穿效应是量子力学中的一个重要现象，描述了微观粒子在经典力学中无法实现的穿越势垒的行为。
隧道效应在化学反应中的应用隧道效应是量子力学的一个现象，它是描述粒子（如分子或原子）从一个能量状况向另一个更高或更低能量状况的跃迁中，会在自由能标为正的剖面和转化态之间发生“隧道效应”的现象。
在化学反应中，隧道效应是指当化学反应过程中反应物的振动能量大于转换态的势垒能量时，反应物分子的振动波动在穿透势垒时出现的现象。
隧道效应的发现，使化学反应的理论有了新的解释。
在传统的化学反应理论中，化学反应中最有意义的是碰撞理论，化学反应发生是因为反应物分子相互碰撞，并且碰撞的能量要大于活化能。
如果反应物分子的振动能量小于活化能，则不会发生反应。
但经过实验表明，在实际反应中，很多分子的振动能量都小于活化能，但仍能发生反应，这就需要引入隧道效应。
隧道效应在化学反应中起作用的原因是量子力学理论中的不确定性原理。
根据不确定性原理，物质粒子在空间位置和动量上具有不确定性，其测量值不能同时精确确定。
这就意味着，一个分子在反应中，其位置和动量都无法确定，因此，在分子穿透势垒时，分子的位置和动量就会发生量子化。
这种量子化的效应称为隧道效应。
隧道效应在化学反应中的应用非常重要。
隧道效应通常在低温下或者分子的活化能很大时才会发挥作用。
当反应物分子的振动能量小于转化态的能量时，这种效应特别重要。
对于很多常见反应，如质子转移、氧化还原、阳离子和阴离子反应，隧道效应都是非常关键的。
对于阳离子反应和阴离子反应，隧道效应是非常显著的。
在阳离子反应中，隧道效应可用于解释化学键复合和离子转移。
在阴离子反应中，隧道效应可用于解释分子内转移反应和化学键断裂。
此外，隧道效应还可以被应用于化学反应机制的研究。
实际上，在许多情况下，只有引入隧道效应，才能解释实验结果。
例如，石墨烯的制备，就是一个非常好的例子。
在实验中，石墨烯是通过氧化还原反应来制备的。
隧道效应在这个反应中起着非常关键的作用。
实验表明，虽然这个反应需要很大的活化能，但仍能在常温下进行，这就是因为隧道效应的存在。
隧道效应与半导体器件引言：隧道效应是一种量子力学现象，它在半导体器件中起着重要的作用。
本文将探讨隧道效应的原理、应用以及与半导体器件之间的关系。
一、隧道效应的原理隧道效应是指当粒子穿越一个势垒时，即使其能量低于势垒高度，也有一定的概率通过势垒，进入势垒的另一侧。
这种现象是量子力学的基本特性之一，与经典物理学中的障碍物穿越现象不同。
隧道效应的原理可以通过波粒二象性解释。
根据波粒二象性理论，粒子不仅具有粒子性质，还具有波动性质。
当粒子遇到势垒时，根据波动性质，其波函数会在势垒两侧形成干涉，使得粒子在势垒两侧都有一定的概率存在。
二、隧道效应的应用1. 扫描隧道显微镜（STM）扫描隧道显微镜是一种利用隧道效应原理的高分辨率显微镜。
它通过在样品表面和探针之间施加一定的电压，利用隧道电流来感测样品表面的形貌和电子结构。
STM在纳米尺度下具有极高的分辨率，被广泛应用于材料科学、生物学等领域。
2. 隧道二极管隧道二极管是一种基于隧道效应工作的半导体器件。
它利用隧道效应使得电子能够在PN结的势垒处穿越，实现电流的反向传输。
隧道二极管具有快速开关速度和低电压损耗的优点，被广泛应用于高频电路和微波通信系统中。
三、隧道效应与半导体器件隧道效应在半导体器件中起着重要的作用，特别是在纳米尺度下。
随着半导体器件尺寸的不断缩小，经典物理学的规律逐渐失效，而量子力学效应开始显现。
1. 隧道场效应晶体管（TFET）隧道场效应晶体管是一种基于隧道效应工作的新型晶体管。
与传统的金属氧化物半导体场效应晶体管（MOSFET）相比，TFET具有更低的功耗和更高的开关速度。
它利用隧道效应实现电子在源极和漏极之间的穿越，从而实现电流的控制。
2. 隧道调制器件隧道调制器件是一种利用隧道效应调节电流的器件。
它可以通过调节势垒高度或宽度来控制电流的大小，从而实现对信号的调制。
隧道调制器件在通信领域具有重要的应用，可以实现高速、低功耗的数据传输。
结论：隧道效应是一种重要的量子力学现象，广泛应用于半导体器件中。
分类号：本科生毕业论文（设计）题目：一维周期势垒中粒子的隧道效应的计算及应用作者单位：物理学与信息技术学院作者姓名：王乐专业班级：物理学（2）班指导教师（职称）：张林（副教授）论文完成时间：二〇〇八年五月一维周期势垒中粒子的隧道效应的计算及应用王乐（陕西师范大学物理学信息技术学院 物理系 陕西 西安710062） 摘 要：隧道效应是经典物理学中不能理解的量子现象。
本文进一步对一维势垒遂穿问题进行了详细讨论，考察了一维势垒遂穿在隧道扫描显微镜上的应用。
论文最后利用传递矩阵的方法对双势垒和多层势垒的隧道效应问题进行了讨论，给出了n 个势垒遂穿的严格结果。
关键词：势垒，隧道效应，双势垒1 引言隧道效应是微观世界独特的现象，它发生的机制，前人虽然已经做了很好的分析和完美的解释，但隧道效应真正的产生机制还不是很清楚，例如粒子在势垒中究竟如何隧穿，粒子隧穿的渡越时间，隧穿共振的机制等。
人们从量子力学的理论发现无论粒子的能量是E > U 还是E < U ，粒子都会既有反射又有透射：R ≠0，D ≠0，而且根据几率守恒有R+D=1。
虽然这个问题的解答从物理上并不令人满意，但1982年，Binning 和Rohrer 依据隧道效应原理却成功制造出扫瞄隧道显微镜，使人类直接观察和操纵原子成为现实。
隧道效应是应用非常广泛的重要效应，它在集成电路，冷电子发射，核衰变，超灵敏电磁探测器等方面都有一定的应用。
近来又发现了隧道效应中的超光速现象，如果能加以应用，将极大的提高信号传递的速度。
可见隧道效应在微观世界是极为普遍的现象，其在实际应用中有重要价值。
近年来，人们发现一些宏观量，如微颗粒的磁化强度、量子相干器件中的磁通量等也具有隧道效应。
宏观量子效应的研究对基础研究及实用都有着重要意义，它限定了磁带、磁盘进行信息存储的时间极限和器件进一步微型化的极限。
为了更为清晰地认识隧道效应在各种势垒中的隧穿行为，我将从薛定谔方程出发，进一步讨论此类问题。
双抛物线势场中的隧道效应王 鑫(陕西理工学院 物理系2007级物理学3 班 ，陕西 汉中 723000)指导老师：王剑华[摘要]量子力学中的隧道效应是一种重要的物理现象，有着非常广泛的应用. 本文从薜定谔方程出发,讨论了求解双抛物线势场中的隧道效应，给出了相应的透射系数和反射系数，并对其进行讨论，研究其应用。
[关键词] 薜定谔方程与遂道效应；双抛物线势场中粒子的透射系数；双抛物线势场中粒子的透射系数；隧道效应及其应用引言在量子力学发展初期，德布罗意根据光的波粒二象性，提出了物质波假说，即认为微观粒子（电子、质子、中子等）也具有波动性。
由于微观粒子具有波动性因而它在能量E 小于势垒高度时仍能贯穿势垒，这种现象称为隧道效应，隧道效应完全是由于微观粒子具有波动的性质而来的。
1957年，江崎制成了隧道二极管，第一次令人信服地证实了固体中的电子隧道效应的存在。
1960年贾埃弗利用隧道效应测量了超导能隙，验证了超导理论。
1982年德国的宾尼等研制成功第一台扫描隧道显微镜，把隧道效应的应用推向一个新的阶段。
近几年来，人们十分关注分子和半导体量子阱中双势的隧道效应问题研究[4-8]，氨分子作为一个典型的三角锥形模型，早在1927年Hund 就提出量子隧道效应会对三角锥形分子的内部结构有很大的调整作用[1]。
适当选择外部条件便可在不同程度上控制分子结构的稳定性。
近几年来在介观尺度的隧道效应和光子隧道效应方面的研究日益成为热点[1-9]，如在超导技术及纳米技术方面的应用发展较为明显[3]。
本文就双抛物线的隧道效应问题求解并进行讨论[2-3]。
1 薛定谔方程与隧道效应在量子力学中，微观体系的运动状态是用一个波函数来描写的，反映微观粒子运动规律的微分方程是()t r ,ψ对时间的一阶微分方程，即:ψ+ψ∇-=∂ψ∂)(222r U t i μ(1.1) 我们称它为薛定谔方程（Schrödinger equation)，式中)r (U是表征力场的函数。
如果作用在粒子上的力场是不随时间改变的，即力场是以势能)(r U表征的，它不显含时间，这时定态波函数所满足的方程为:ψ=ψ+ψ∇-E r U )(222 μ(1.3) 称为定态薛定谔方程（Schrödinger equation of stationary state )，其中E 表示微观粒子处于这个波函数所描写的状态时的能量，且其能量具有确定值。
设一个粒子，沿x 轴正方向运动，其势能为:⎩⎨⎧=0)(0U x U （2.1）这种势能分布称为一维势垒。
如图2.1所示，故称方势垒。
虽然方势垒只是一种理想的情况，但却是计算一维运动粒子被任意场散射的基础。
粒子在0x <区域内，若其能量小于势垒高度，经典物理来看是不能超越势垒达到0x >的区域。
在量子力学中，情况则不一样。
为了讨论方便，我们把整个区域分为三个区域：Ⅰ()0x ≤，Ⅱ()0x a ≤≤，Ⅲ()x a ≥图2.1 一维方型势垒为了方便起见，将整个空间划分为三个区域Ⅰ、Ⅱ、Ⅲ区，则其定态薛定谔方程为22222220 (0,),2()0(0).d E x x a dx d E U x a dx μμ⎧ψ+ψ=≤≥⎪⎪⎨ψ⎪+-ψ=≤≤⎪⎩(2.2) 当0U E >时，透射系数T ，反射系数为R2212222222122122222122222222122124()sin 4()sin ()sin 4k k T k k k a k k k k k a R k k k a k k ⎧=⎪-+⎪⎨-⎪=⎪-+⎩当0U E <时，只需令32ik k =即可，透射系数)0(a x ≤≤ ),0(a x x ≥≤（2.3）（2.4）2213222222133134()4k k T k k sh k a k k =++ (2.5) 反射系数为1R T =- (2.6)如果粒子能量比势垒高度小得多，即0U E <<，同时势垒的宽度a 不太大，以致13>>a k ，则a k ak e e33->> ，此时233a k ea shk ≈，于是32213222222131341()44k a k k T k k e k k ≈++ 322313111()116k ak k e k k =++ (2.7))(1331k k k k +为恒大于1的数值，当13>>a k 时432>>a k e3200k aT T e T e -== (2.8)当0E U >的时候，按照经典力学观点，在0E U >情况下，粒子应畅通无阻的全部通过势垒，而不会在势垒上发生反射。
而在微观粒子的情形，则会发生发射。
当0E U <的时候，从解薛定谔方程的结果来看，在势垒内部存在波函数。
即在势垒内部找出粒子的概率不为零，同时在x a >区域也存在波函数，所以粒子还可能穿过势垒进入x a >区域。
粒子在总能量E 小于势垒高度时仍能贯穿势垒的现象称为遂道效应。
其中221302221316()k k T k k =+ 它的数量级接近于1，所以透射系数随势垒的加宽或加高而减小。
由上面的结果我们可以看到，微观粒子被势垒散射有与宏观粒子完全不同的效应。
当一个宏观粒子的能量E 大于势垒高度0U 时，此粒子将通过区域（Ⅱ）而进入区域（Ⅲ）。
但是对于一个能量0U E >的微观粒子，不但有穿过势垒的可能，而且还有被反射的可能。
如果一个宏观粒子的能量0U E <，则当此粒子在区域（Ⅰ）内由左向右运动到达势垒边界时将被反射，所以粒子不可能穿过区域（Ⅱ）而进入区域（Ⅲ）。
但是对于一个0U E <的微观粒子却不然，它既有被反射的可能，也有穿透势垒而进入区域（Ⅲ）的可能，这种贯穿势垒的效应称为隧道效应。
2 双抛物线势场中粒子的波函数下面计算xα2- a b 0 c d α2()()2010220202() 20,() 02.V V x x a V x aV V x x a V x a αα⎧=-++-≤≤⎪⎪⎨⎪=--+≤≤⎪⎩（4.1）各个薛定谔方程为222222222222202,()0 20,()0 02,20 2.d E x d x d m x a n x d xd m x a n x d x d E x d x μαααμα⎧ψ+ψ=≤-⎪⎪ψ⎪+++ψ=-<≤⎪⎪⎨ψ⎪+-+ψ=<≤ψ+ψ=≤⎩⎪⎪⎪⎪ (4.2)其中m a U =2202 μ n U E =-)(202 μ令() x V E k 11(2-=μ () x V E k 22(2-=μ () x V E K 11(2--=μ () x V E K 22(2--=μ如上图所示，假设粒子以一定的能量E 从左入射，碰到势垒V （x ），设V （x ）变化比较缓慢，而且入射粒子能量E 不太靠近V （x ）的峰值，此时可以用W.K.B.法来处理粒子穿透势垒的现象。
按照经典力学，粒子在x=a 处被碰回，但按照量子力学，考虑到粒子的波动性，粒子有一定的几率穿透势垒。
当然，在许多情况下，这种几率是很小的。
现在我们就来计算双势垒穿透几率T 的大小。
在A 区远离a 处,由(3.6)式得波函数是⎪⎭⎫⎝⎛---⎪⎭⎫ ⎝⎛--⎰⎰+=ψax axdx k i dx k i ek A eAk 4211'4211111ππ, (4.3)在C 区远离b 处,由(3.6)式得波函数是⎪⎭⎫⎝⎛---⎪⎭⎫⎝⎛--⎰⎰+=ψxb xb dx k i dx k i ek B eBk 4211'4211311ππ , (4.4)而根据连接关系(3.8),(3.9),则在区域B 中的W.K.B.近似解应为⎰+⎰+⎰-⎰=ψ------bxbx bxbx dx K dx K dx K dx K e K iB e K B e iBK e BK 1111211'211'21121122121=⎰⎰⎰⎰--------++-x axaxaxadx K dx K dx K dx K e K iB e K B e iBK e BK 1111211'1211'21112112121ττ.(4.5)其中, ⎰=badxK e 11τ.利用a 处的连接公式(3.10),(3.11)在区域A 中的W.K.B.近似解(4.3)应为⎪⎭⎫ ⎝⎛----=ψ⎰⎰--ax a x k iBk dx k Bk 4cos 2)4sin(21112111112111πτπτ⎪⎭⎫ ⎝⎛-+--+⎰⎰--ax a x k k iB dx k k B 4cos 2)4sin(211111'111211'πτπτ=⎪⎭⎫⎝⎛-⎰++-ax dx k i e B B k i 1)]221()221([211'11211ττττ +⎪⎭⎫⎝⎛--⎰--+-a xdx k i e B B k i 1)]221()221([211'11211ττττ , (4.6)同理,在D 区域的波函数为⎪⎭⎫⎝⎛---⎪⎭⎫⎝⎛--⎰⎰+=ψcx cx dx k i dx k i ek C eCk 4211'4211411ππ , (4.7)在F 区域,远离d 处,由于只有投射波,没有反射波,所以,W.K.B 近似解为⎪⎭⎫⎝⎛--⎰=ψxd dx k i eDk 421262π=⎰⎰-+⎪⎭⎫ ⎝⎛---x d x d dx k iDk dx k Dk )4sin(4cos 2212212ππ , (4.8)由(3.8),(3.9) 则在区域E 中的W.K.B.近似解应为⎰--⎰---=ψx c x c dxK dx K e iDK e DK 22221212212521ττ.(4.9) 其中, ⎰=dcdxK e 22τ,⎪⎭⎫ ⎝⎛----=ψ⎰⎰--cx c x k iDk dx k Dk 4cos 2)4sin(212122122122124πτπτ⎰--+⎰-=-----cx cx dx k i dx k i ek iD e k iD )4(21222)4(2122222)221(2)221(2ππττττ . (4.10) 利用波函数43,ψψ及其微商在x=0处的连续性得方程组并解之得 )221(222ττα--=i e iD B (4.11) )221(222'ττα+-=-i e iD B (4.12) 其中)(12⎰⎰-=bcdx k dx k i α3 双抛物线势场中粒子的透射系数下面计算粒子在双抛物线势场中的透射系数。
