排队论基础

排队论的基本原理排队论是一门研究排队系统的数学理论，它主要研究排队系统中顾客到达、排队、服务和离开等过程的规律性和性能指标。

排队论的基本原理包括到达过程、排队规则、服务机制和排队系统性能指标等内容，下面将逐一介绍。

首先，到达过程是指顾客到达排队系统的时间间隔和规律。

在排队论中，到达过程通常用到达率λ来描述，它表示单位时间内平均到达的顾客数。

到达过程的规律性对于排队系统的性能有着重要的影响，合理的到达过程模型可以帮助我们更好地设计和优化排队系统。

其次，排队规则是指顾客在排队系统中等待和被服务的规则。

常见的排队规则包括先来先服务（FCFS）、最短作业优先（SJF）、最短剩余服务时间优先（SRTF）等。

不同的排队规则对于系统的性能指标会产生不同的影响，因此在实际应用中需要根据具体情况选择合适的排队规则。

服务机制是指顾客在排队系统中接受服务的方式和规则。

服务机制通常包括单一服务台、多个服务台、顾客限制、服务时间限制等内容。

合理的服务机制可以有效地提高系统的服务效率和顾客满意度，因此在设计排队系统时需要充分考虑服务机制的选择和优化。

最后，排队系统性能指标是评价排队系统性能优劣的重要指标。

常见的性能指标包括顾客平均等待时间、系统平均等待时间、系统繁忙度、系统利用率等。

这些指标可以帮助我们全面地了解排队系统的运行情况，从而进行合理的优化和改进。

在实际应用中，排队论的基本原理可以帮助我们更好地理解和分析排队系统，从而提高系统的效率和服务质量。

通过合理地设置到达过程、排队规则和服务机制，以及监控和优化系统性能指标，可以有效地改善排队系统的运行效果，满足顾客的需求，提升服务水平。

综上所述，排队论的基本原理是研究排队系统中各个环节的规律性和性能指标，通过合理地设置和优化这些环节，可以有效地提高排队系统的运行效率和服务质量，满足顾客的需求，实现经济效益和社会效益的双赢。

希望本文对排队论的基本原理有所帮助，谢谢阅读！。

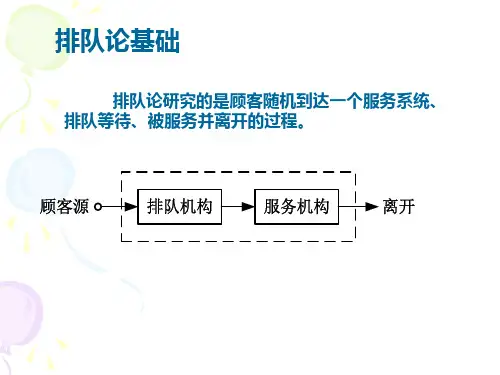
运筹优化（⼗六）--排队论基础及其最优化求解排队过程的⼀般表⽰下图1就是排队过程的⼀般模型。

各个顾客由顾客源(总体)出发,到达服务机构 (服务台、服务员)前排队等候接受服务, 服务完成后就离开。

排队结构指队列的数⽬和排列⽅式 , 排队规则和服务规则是说明顾客在排队系统中按怎样的规 则、次序接受服务的。

我们所说的排队系统就指图中虚线所包括的部分。

排队系统的组成和特征⼀般的排队系统都有三个基本组成部分 : 1输⼊过程 ; 2排队规则 ; 3服务机构。

1. 输⼊过程输⼊即指顾客到达排队系统 , 可能有下列各种不同情况 , 当然这些情况并不是彼此排斥的。

(1) 顾客的总体(称为顾客源)的组成可能是有限的,也可能是⽆限的。

上游河⽔流⼊⽔库可以认为总体是⽆限的 , ⼯⼚内停机待修的机器显然是有限的总体。

(2) 顾客到来的⽅式可能是⼀个⼀个的, 也可能是成批的。

例如到餐厅就餐就有单个到来的顾客和受邀请来参加宴会的成批顾客，我们将只研究单个到来的情形。

(3) 顾客相继到达的间隔时间可以是确定型的, 也可以是随机型的。

(4) 顾客的到达可以是相互独⽴的,就是说,以前的到达情况对以后顾客的到来没有影响 , 否则就是有关联的 。

(5) 输⼊过程可以是平稳的,或称对时间是齐次的,是指描述相继到达的间隔时间分布和所含参数(如期望值、⽅差等)都是与时间⽆关的, 否则称为⾮平稳的。

2. 排队规则(1) 顾客到达时, 如所有服务台都正被占⽤,在这种情形下顾客可以随即离去, 也可以排队等候。

随即离去的称为即时制或称损失制 , 因为这将失掉许多顾客 ; 排队等候的称为等待制。

普通市内电话的呼唤属于前者 , ⽽登记市外长途电话的呼唤属于后者。

对于等待制,为顾客进⾏服务的次序可以采⽤下列各种规则: 先到先服务, 后到先服 务 , 随机服务 , 有优先权的服务等。

先到先服务 , 即按到达次序接受服务 , 这是最通常的情形。

后到先服务,如乘⽤电梯的顾客常是后⼊先出的。

排队论基础一、课程说明课程编号：130531Z10课程名称：排队论基础/Fundamentals of Queueing Theory课程类别：选修学时/学分：32/3先修课程：概率论适用专业：统计学；数学与应用数学和信息与计算数学教材、教学参考书：1.陆传赉. 排队论[M],第2版.北京：北京邮电大学出版社，20092.唐应辉，唐小我. 排队论—基础与分析技术[M].北京：科学出版社，20063.邓永录. 随机模型及其应用[M].北京：高等教育出版社，1994二、课程设置的目的意义排队论又名随机服务系统理论，是研究拥挤现象的一门数学学科，它通过研究各种服务系统在排队等待中的概率特性，来解决系统的最优设计和最优控制。

排队论是随机运筹学的重要分支，也是应用概率的重要分支，所研究的问题有很强的实际背景。

随着计算机技术的迅猛发展，排队论的科学研究日新月异，其应用领域也不断扩大。

目前，排队论的科学研究成果已广泛应用于通信工程、交通物流运输、生产与库存管理、计算机系统设计、计算机通信网络、军事作战、制造系统和系统可靠性等众多领域，并取得了丰硕成果。

排队论在科学技术及国民经济发展中起到了直接的重要作用，而且已成为从事通信、计算机、工业工程等领域的专家、工程技术人员和管理人员必不可少的重要数学工具之一。

通过本课程的学习，让学生掌握排队论的基本理论与方法，能对现实生活中的一些排队现象进行分析和建模；通过与不同的学科知识相结合，能对所考虑具体问题的分析结果和模型进行评价，并给出合理的设计和控制机制。

本课程的学习，不仅帮助学生掌握排队系统分析和建模的基本技能，了解本学科的特点和发展前沿，而且让学生在资料收集、建模与计算、结果的分析与评价等整个过程得到较全面的训练。

三、课程的基本要求知识要求：掌握排队论的基本理论与方法；掌握转移率矩阵、补充变量法、嵌入马氏链以及计算马氏排队网络平稳分布的各种基本方法。

了解排队论在管理科学中应用的若干前沿发展方向。

排队论的基本原理：
排队论（Queuing Theory）是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法，其基本原理主要包括以下几个方面：
1.排队系统的组成：排队系统通常由输入过程、排队规则和服务机构三个部分组成。

输入过程是指顾客到达服务系统的随机方式，排队规则是指顾客到达后按照怎样的规则排队等待服务，服务机构则是指服务的提供方式。

2.概率论和随机过程：排队论中需要用到概率论和随机过程的数学知识，如概率分布、
期望、方差等。

这些知识用于描述顾客到达和服务时间的统计规律。

3.状态分析：排队论中的状态分析主要是指对排队系统的状态进行描述和分类，如空
闲状态、忙状态等。

通过对状态的分析，可以确定系统的各种性能指标，如等待时间、队长等。

4.最优化原理：排队论中的最优化原理是指通过调整系统参数，如服务时间、服务速
率等，使得系统的性能指标达到最优。

最优化原理的目的是在满足一定约束条件下，使系统的某种性能指标达到最优。

5.可靠性理论：可靠性理论是排队论中的一个重要组成部分，它研究的是系统可靠性
的概念、指标和计算方法。

可靠性理论可以帮助我们分析系统的可靠性、故障率和可用性等方面的问题，为系统的设计和优化提供依据。

运筹学中的排队论分析与应用运筹学是一门研究如何最优化决策的学科。

在现代社会中，许多场景下都存在排队现象，例如银行、超市、机场等场所。

排队论作为运筹学的一个重要分支，专门研究如何通过合理的排队策略来优化服务效率与用户体验。

本文将介绍排队论的基本原理、应用场景以及如何利用排队论进行实际问题的分析与解决。

一、排队论的基本原理排队论是研究排队系统的理论与方法，其基本原理包括排队模型、排队规则以及排队指标。

1. 排队模型排队模型是对排队系统进行抽象和建模的过程，常用的排队模型有M/M/1、M/M/c、M/G/1等。

其中，M表示顾客到达过程符合泊松分布，而服务过程符合指数分布；1表示一个服务台，c表示多个服务台；G表示总体服从一般分布。

2. 排队规则排队规则是指在排队系统中，顾客到达和离开的规则。

常用的排队规则有先到先服务（First-Come-First-Serve，简称FCFS）、最短作业优先（Shortest Job First，简称SJF）、优先级法则等。

3. 排队指标排队指标是对排队系统性能的度量，常用的排队指标包括平均等待时间、平均逗留时间、系统繁忙度等。

这些指标可以帮助我们评估排队系统的效率，并进行比较和优化。

二、排队论的应用场景排队论的应用场景非常广泛，几乎可以涵盖各个行业。

下面以几个典型的应用场景为例，介绍排队论在其中的分析与应用。

1. 银行排队银行是排队论的典型应用场景之一。

通过排队论的分析，银行可以确定合理的柜台数量和工作人员配置，以减少客户的等待时间和提高服务效率。

此外，银行还可以考虑引入预约系统、自助服务等方式，进一步优化排队系统。

2. 售票窗口排队售票窗口也是一个常见的排队场景，如电影院、火车站等。

利用排队论，可以根据顾客到达的速率和服务时间的分布，预测等待时间，并提前安排足够的窗口进行服务，以提高售票效率和用户体验。

3. 交通信号灯优化交通信号灯的优化也可以借助排队论的方法。

通过对道路上车辆到达和通过的流量进行统计和分析，可以调整信号灯的信号周期和配时方案，以减少交通拥堵和减少等待时间。