大学物理质点运动描述

大学物理第1章质点运动学质点运动学是物理学中研究物体运动的学科，它是物理学的一个重要分支，是学习物理的基础之一。

一、质点运动学的概念质点运动学是研究质点运动的学科，它把物体看作质点，即把物体看成一个点，而不考虑其体积大小。

质点运动学的主要研究内容包括：位置、速度、加速度等运动量的描述，以及运动的曲线形状、动量、能量等方面的分析。

二、质点的运动质点的运动可以分为匀速运动和非匀速运动两种情况。

1.匀速运动匀速运动是指质点在单位时间内沿着同一直线等距离地移动的运动。

匀速运动的速度大小是恒定的，可以用速度公式v=d/t来计算。

2.非匀速运动非匀速运动是指质点在单位时间内沿任意曲线路径移动的运动。

非匀速运动中质点的速度大小是变化的，需要用微积分的方法进行分析和计算。

三、质点运动中的基本物理量在质点运动中，需要描述质点的运动状态和变化情况。

主要的量包括：1.位置位置是指质点在空间中所处的位置，通常使用坐标表示。

我们可以通过坐标系建立一个参照系，来描述质点的位置。

2.位移位移是指质点从一个位置到另一个位置的距离和方向，通常用符号Δr表示。

位移的大小可以用位移公式Δr=r2-r1来计算。

3.速度速度是指质点在单位时间内所改变的位置，通常用符号v 表示。

速度的大小可以用速度公式v=Δr/Δt来计算。

4.加速度加速度是指质点在单位时间内速度所改变的量，通常用符号a表示。

加速度的大小可以用加速度公式a=Δv/Δt来计算。

四、质点的曲线运动在质点运动中，一些运动路径可能是曲线运动。

曲线运动的路径通常可以用弧长s、曲率半径r、圆心角等来表征。

1.弧长弧长是指质点在曲线路径上所走过的曲线长度，通常用符号s表示。

弧长的大小可以用弧长公式s=rθ来计算。

2.曲率半径曲率半径是指曲线在任一点上的曲率半径，通常用符号r 表示。

曲率半径可以根据曲线的形状计算得出。

3.圆心角圆心角是指质点所在的路径所对应的圆所对应的圆心角度数，通常用符号θ表示。

大学物理基础知识质点运动的描述与分析质点运动是大学物理基础知识中的重要内容，它描述了物体在空间中的运动状态以及造成其运动的各种原因。

本文将从质点运动的基本概念、描述运动的方式以及运动分析等几个方面展开论述。

一、质点运动的基本概念在物理学中，质点被定义为一个非常小、不具有大小和形状的物体，仅具有质量。

质点具有位置、速度和加速度等运动状态。

质点运动可以按照时间发生的方式来描述，常见的有匀速直线运动、变速直线运动、曲线运动等。

二、描述运动的方式为了准确地描述和分析物体的运动，需要引入一些物理量来描述质点的运动状态。

常见的运动描述物理量有位移、速度和加速度。

1. 位移位移是指物体从起点到终点的位置变化。

位移的大小和方向决定了两个时刻物体的位置差异。

位移可以用矢量来表示，即具有大小和方向。

当物体做直线运动时，位移的方向与物体运动方向保持一致。

位移的计算公式为Δx = x₂ - x₁。

2. 速度速度是指单位时间内位移的变化率。

速度表征了物体运动的快慢以及方向，是矢量量。

平均速度可以用位移与时间的比值来表示，即v =Δx / Δt。

而瞬时速度则是时间无限趋近于零时的速度，可以通过取限极的方式求得。

3. 加速度加速度是指单位时间内速度的变化率。

加速度描述了物体运动状态的改变情况，也是矢量量。

平均加速度可以用速度变化与时间的比值来表示，即a = Δv / Δt。

而瞬时加速度则是时间无限趋近于零时的加速度。

三、运动分析在质点运动的分析中，常常关注的问题有速度与位移之间的关系、加速度与速度之间的关系以及相互作用力对运动的影响等。

1. 速度与位移之间的关系在质点做匀速直线运动时，位移和速度之间的关系是简单的线性关系。

根据定义，平均速度等于位移与时间的比值。

而无论加速度大小，匀速直线运动时的瞬时速度保持不变。

因此，可以得出结论，在匀速直线运动中，速度与位移呈线性关系。

2. 加速度与速度之间的关系加速度描述了速度变化的快慢以及方向的改变。

大学物理质点运动学总结一、引言在大学物理课程中，运动学是物理学的基础，它研究物体的运动状态和运动规律。

其中，质点运动学是运动学的一部分，主要研究质点的运动性质和运动规律。

下面将对大学物理质点运动学进行总结。

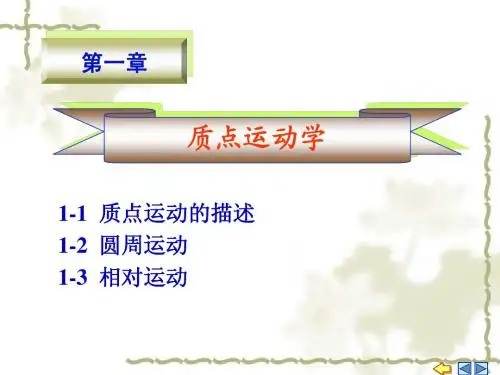
二、质点的运动描述1. 位置和位移质点在运动过程中，位置可以用空间直角坐标系或极坐标系来描述。

而位移是指物体从初始位置到最终位置的变化量，它是个矢量量，具有大小和方向。

2. 速度与速度的计算方法速度是指单位时间内位移的变化量，可以用瞬时速度和平均速度来描述。

瞬时速度是指某一瞬间的速度，可以通过求导位移对时间的导数得到。

平均速度是指物体在一段时间内总位移与总时间的比值。

3. 加速度与加速度的计算方法加速度是指单位时间内速度的变化量，也是个矢量量。

可以用瞬时加速度和平均加速度来描述。

瞬时加速度是指某一瞬间的加速度，可以通过求导速度对时间的导数得到。

平均加速度是指物体在一段时间内总速度变化与总时间的比值。

三、常见的运动规律1. 一维运动规律一维运动规律描述了在一条直线上运动的物体的运动规律。

其中最重要的是匀速直线运动规律和匀加速直线运动规律。

匀速直线运动规律指出，当物体在匀速直线运动时，其位移与时间成正比。

匀加速直线运动规律指出，在匀加速直线运动中，物体的位移与时间的关系是二次函数。

2. 斜抛运动规律斜抛运动是指物体沿着一个初速度方向在空中做抛体运动的一种情况。

在斜抛运动中，物体的水平速度保持恒定，垂直速度受到重力的作用而发生改变。

斜抛运动的水平运动和垂直运动可以分开来考虑，通过合成两个运动，可以得出物体的轨迹和运动规律。

3. 圆周运动规律圆周运动是指物体在半径相同的圆内以恒定速度做匀速圆周运动的一种情况。

在圆周运动中，质点的速度方向始终垂直于半径的方向，因此质点在圆周上的运动轨迹是一个圆。

圆周运动的相关公式可以由质点完成单位时间所走过的弧长与所需的时间的比值来推导。

四、运动学的应用1. 自由落体问题自由落体是指物体在无空气阻力情况下，在重力作用下自由垂直下落的一种运动。

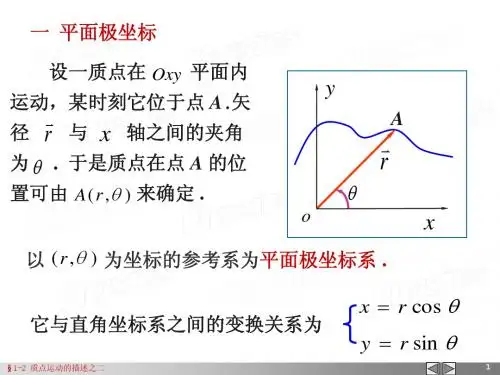
《大学物理学C 》课程基本内容第一章 质点的运动1．直角坐标系、极坐标系、自然坐标系※2．质点运动的描述：位置矢量r 、位移矢量r ∆=)()(t r t t r-∆+、运动方程)(t r r =。

在直角坐标系中,k t z j t y i t x t r)()()()(++=速度：t rv d d=； 加速度：22d d d d t r t v a == 在直角坐标系中，速度k v j v i v v z y x ++=,加速度k a j a i a a z y x++=自然坐标系中，速度 τ v v =＝τts d d ，加速度t n a a a +==n r v t v 2d d +τ 在极坐标系中,角量的描述：角速度t d d θω=，角加速度22d d d d t t θωα==3．运动学的两类基本问题：第一类问题:已知运动方程求速度、加速度等。

此类问题的基本解法是根据各量定义求导数。

第二类问题:已知速度函数(或加速度函数)及初始条件求运动方程。

此类问题的基本解法是根据各量之间的关系求积分。

例如据txv d d =，可写出积分式⎰x d ＝⎰t v d .由此求出运动方程)(t x x =。

4．相对运动：位移:t u r r ∆+'∆=∆ ，速度：u v v+'=,加速度：0a a a +'=第七章 气体动理论1．对“物质的微观模型”的认识；对“理想气体”的理解。

※2．理想气体的压强公式23132v n p k ρε==，其中221v m k =ε※理想气体物态方程：RT MmpV =或 nkT p =理解压强与微观什么有关，即压强的物理含义是什么.※3．理想气体分子的平均平动动能与温度的关系：kT k 23=ε 理解温度与微观什么有关，即温度的物理含义。

※4．能量均分定理：气体处于平衡态时，分子每个自由度上的平均能量均为2kT概念：自由度※理想气体内能公式：RT iM m E 2=5．麦克斯韦气体分子速率分布律 ※麦克斯韦气体分子速率分布函数：定义：vNN v f d d 1)(=函数：22232π2π4)(v v v kTm ekT m f -⎪⎭⎫⎝⎛= 以及v v f NNd )(d =；v v Nf N d )(d =；⎰21d )(v v v v Nf ；⎰21d )(v v v v f 等表示的物理含义。