概率及概率密度分布函数解读

分布函数密度函数分布函数和密度函数是概率论中常用的两个概念，用来描述随机变量的性质和分布规律。

本文将详细介绍分布函数和密度函数的概念、性质以及它们在概率论和统计学中的应用。

一、分布函数分布函数（Cumulative Distribution Function，简称CDF）是描述随机变量X的概率分布情况的函数。

对于任意实数x，分布函数F(x)的定义如下：F(x) = P(X ≤ x)其中，P(X ≤ x)表示随机变量X的取值小于等于x的概率。

分布函数具有以下几个重要性质：1. F(x)是一个非递减函数，在整个实数轴上单调不减。

2. 当x趋近于负无穷时，F(x)趋近于0；当x趋近于正无穷时，F(x)趋近于1。

3. F(x)是一个右连续函数，即在任意点x处，F(x)的右极限等于F(x)的值。

分布函数的图像通常是一个右连续的阶梯函数，从0开始逐渐上升，最终趋近于1。

分布函数的性质决定了它在统计推断中的重要作用。

二、密度函数密度函数（Probability Density Function，简称PDF）是描述连续型随机变量X的概率分布情况的函数。

对于任意实数x，密度函数f(x)的定义如下：f(x) = dF(x)/dx其中，dF(x)表示分布函数F(x)在x处的微分。

密度函数具有以下几个重要性质：1. f(x)是非负函数，即在整个实数轴上大于等于0。

2. 在整个实数轴上，f(x)的积分等于1，即∫f(x)dx = 1。

密度函数的图像通常是一个曲线，表示随机变量X在不同取值上的概率分布情况。

由于密度函数是概率密度的描述，因此它的取值可以大于1，但概率值仍然在[0,1]之间。

三、分布函数和密度函数的关系对于连续型随机变量X，它的分布函数F(x)和密度函数f(x)之间存在如下关系：F(x) = ∫f(t)dt (从负无穷到x的积分)f(x) = dF(x)/dx也就是说，分布函数是密度函数的积分，密度函数是分布函数的导数。

概率分布函数与概率密度函数概率分布函数和概率密度函数是统计学中常见的两个重要概念，它们在描述随机变量分布特征时起着至关重要的作用。

下面我们将分别介绍概率分布函数和概率密度函数的概念、特点和应用。

一、概率分布函数概率分布函数又称为累积分布函数，是描述随机变量取值的概率分布规律的函数。

对于任意一个实数t，概率分布函数F(t)定义为随机变量X的取值小于等于t的概率，即F(t)=P(X≤t)。

概率分布函数的性质有以下几个特点：1. F(t)是一个单调非减的函数，即对于任意s和t（s≤t），有F(s)≤F(t)。

2. F(t)在整个实数轴上取值范围为[0,1]。

3. 当t趋近于负无穷时，F(t)趋近于0；当t趋近于正无穷时，F(t)趋近于1。

4. 概率分布函数是一种分步函数，具有不连续点。

在不连续点上，概率分布函数的值对应着概率的跳跃。

概率分布函数在统计学中有着广泛的应用，可以帮助研究者了解随机变量的分布情况，进而进行参数估计、假设检验、置信区间估计等统计分析工作。

二、概率密度函数概率密度函数是描述随机变量取值的密度分布的函数，通常用f(t)表示。

对于连续型随机变量X，如果存在一个函数f(t)，对于任意实数区间[a,b]，有P(a≤X≤b)= ∫[a,b] f(t)dt。

概率密度函数的性质如下：1. 概率密度函数在整个定义域上非负，即f(t)≥0。

2. 概率密度函数的积分在整个定义域上等于1，即∫(-∞,+∞) f(t)dt=1。

3. 概率密度函数f(t)与概率分布函数F(t)之间存在积分关系，即F(t)=∫(-∞,t) f(u)du。

4. 概率密度函数的图形代表了随机变量在不同取值上的密度大小，可以直观地表示随机变量的分布情况。

概率密度函数在连续型随机变量的分布描述中占据重要地位，例如正态分布、指数分布、均匀分布等常见的概率分布都可以通过概率密度函数来描述其分布规律。

综上所述，概率分布函数和概率密度函数是统计学中两个重要的概念，它们分别适用于离散型随机变量和连续型随机变量的分布描述。

如何理解概率分布函数和概率密度函数概率分布函数和概率密度函数都是统计学和概率论中常用的概念，用于描述随机变量在不同取值上的概率分布。

虽然两者的表达方式不同，但其含义和作用相似。

概率分布函数（Probability Distribution Function，简称PDF）是一种函数，描述了随机变量X的概率分布情况。

对于连续型随机变量，概率分布函数定义为随机变量X小于或等于一些给定取值x的概率。

它通常用F(x)来表示，即F(x) = P(X <= x)。

概率分布函数具有以下性质：1.对于所有的x，F(x)的取值在0到1之间。

2.当x趋于负无穷时，F(x)趋近于0。

3.当x趋于正无穷时，F(x)趋近于14.F(x)是一个非降函数，即对于任意的a<b，有F(a)<=F(b)。

概率密度函数（Probability Density Function，简称PDF）是一种函数，描述了连续型随机变量取一些特定值的概率密度。

概率密度函数通常用f(x)来表示，即对于连续型随机变量X，f(x)表示其在一些取值x处的密度。

概率密度函数具有以下性质：1.对于任意的x，概率密度函数的值大于等于0，即f(x)>=0。

2. 整个样本空间上的积分等于1，即∫f(x)dx = 1、这表示随机变量取任意值的概率之和为13. 概率密度函数与概率分布函数之间的关系为：概率密度函数为概率分布函数的导数。

即f(x) = dF(x)/dx。

概率分布函数和概率密度函数的关系可以通过求导和积分互相转化。

对于连续型随机变量X，其概率分布函数可以通过概率密度函数进行计算，即F(x) = ∫f(t)dt，其中t的取值范围为(-∞, x)。

反过来，概率密度函数可以通过概率分布函数求导得到，即f(x) = dF(x)/dx。

理解概率分布函数和概率密度函数的重要性在于可以通过它们来描述和分析随机变量的概率分布特征。

概率分布函数可以用于计算随机变量取不同取值的概率，以及计算概率的分布情况，例如均值、方差和偏度等。

分布函数与概率密度函数分析：概率分布的数学描述概率分布是概率论中的一个重要概念，用于描述随机变量的可能取值及其对应的概率。

在概率论中，有两种常用的概率分布函数，即分布函数和概率密度函数。

本文将分别对这两种函数进行详细的分析，探讨它们对概率分布的数学描述。

一、分布函数分布函数，又称分布累积函数，是描述随机变量的取值小于或等于给定值的概率。

它通常用字母F(x)表示。

对于随机变量X，其分布函数F(x)的数学定义为：F(x) = P(X ≤ x)其中P表示概率，X ≤ x表示随机变量X的取值小于或等于x。

分布函数是一个非递减的右连续函数。

通过分布函数，可以得到随机变量X在某个取值x处的概率。

具体而言，对于一个连续型随机变量X，其概率密度函数f(x)是分布函数F(x)的导数。

而对于一个离散型随机变量X，其概率质量函数p(x)是分布函数F(x)的跳跃点的高度。

二、概率密度函数概率密度函数，简称密度函数，是用来描述连续型随机变量的概率分布的函数。

通常用字母f(x)表示。

对于随机变量X，其概率密度函数f(x)的数学定义为：f(x) = dF(x)/dx其中dF(x)表示F(x)的微分，dx表示x的微分。

概率密度函数具有以下性质：1. f(x) ≥ 0，即概率密度函数非负；2. ∫f(x)dx = 1，即概率密度函数的总面积为1；3. 在一段区间[a, b]上的概率可以通过计算f(x)在该区间上的积分得到。

通过概率密度函数，可以计算连续型随机变量在某个区间内的概率。

具体而言，连续型随机变量X在区间[a, b]上的概率可以表示为：P(a ≤ X ≤ b) = ∫[a, b]f(x)dx三、分布函数与概率密度函数的关系对于连续型随机变量X，其分布函数F(x)与概率密度函数f(x)之间存在如下关系：F(x) = ∫[−∞, x]f(t)dt即分布函数F(x)是概率密度函数f(x)的积分。

反之，如果已知一个连续型随机变量X的分布函数F(x)，可以通过对F(x)求导来得到概率密度函数f(x)。

如何理解概率分布函数和概率密度函数概率分布函数（Probability Distribution Function，简称PDF）和概率密度函数（Probability Density Function，简称PMF）是概率论中用于描述随机变量的概率分布的两种函数形式。

概率分布函数是用于连续随机变量的，它描述了随机变量落在一些区间内的概率。

概率分布函数的定义如下：对于连续随机变量X，其概率分布函数F(x)表示随机变量X小于等于一些值x的概率，即F(x)=P(X<=x)。

概率分布函数具有以下特征：1.F(x)的值域在0到1之间。

2.F(x)是非递减的，即对于任意的x1<x2，F(x1)<=F(x2)。

3.F(x)在负无穷到正无穷的范围内是连续的，除了在一些点上可能存在跳跃。

4.F(x)在负无穷到正无穷的范围内是右连续的，即F(x+)=F(x)。

概率密度函数则是用于描述连续随机变量的密度分布情况。

概率密度函数的定义如下：对于连续随机变量X，其概率密度函数f(x)是一个非负函数，满足对于任意的实数x，有P(a <= X <= b) = ∫[a,b] f(x)dx。

概率密度函数具有以下特征：1.概率密度函数的取值范围是非负的，即f(x)>=0。

2. 概率密度函数的积分是等于1的，即∫[-∞, +∞] f(x)dx = 13.概率密度函数在一些点上的值并不代表在该点上的概率，而是代表了在该点附近的概率密度。

概率分布函数和概率密度函数在描述随机变量的分布特征时起到了不同的作用。

概率分布函数是用于给出一些具体值小于等于一些给定值的概率，而概率密度函数则是给出在一些区间内连续变量出现的概率。

具体地说，给定一个连续随机变量X，可以通过概率分布函数F(x)来计算出P(X<=x)的概率，而要计算出P(a<=X<=b)的概率，则需要使用概率密度函数f(x)进行积分计算。

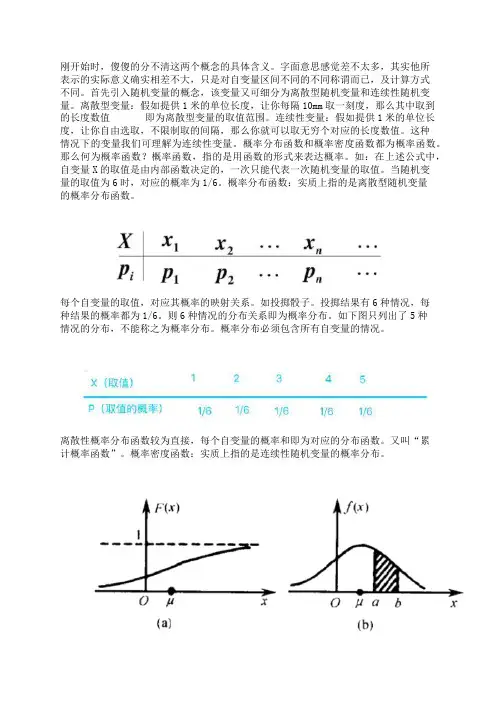
刚开始时，傻傻的分不清这两个概念的具体含义。

字面意思感觉差不太多，其实他所表示的实际意义确实相差不大，只是对自变量区间不同的不同称谓而已，及计算方式不同。

首先引入随机变量的概念，该变量又可细分为离散型随机变量和连续性随机变量。

离散型变量：假如提供1米的单位长度，让你每隔10mm取一刻度，那么其中取到的长度数值即为离散型变量的取值范围。

连续性变量：假如提供1米的单位长度，让你自由选取，不限制取的间隔，那么你就可以取无穷个对应的长度数值。

这种情况下的变量我们可理解为连续性变量。

概率分布函数和概率密度函数都为概率函数。

那么何为概率函数？概率函数，指的是用函数的形式来表达概率。

如：在上述公式中，自变量X的取值是由内部函数决定的，一次只能代表一次随机变量的取值。

当随机变量的取值为6时，对应的概率为1/6。

概率分布函数：实质上指的是离散型随机变量的概率分布函数。

每个自变量的取值，对应其概率的映射关系。

如投掷骰子。

投掷结果有6种情况，每种结果的概率都为1/6。

则6种情况的分布关系即为概率分布。

如下图只列出了5种情况的分布，不能称之为概率分布。

概率分布必须包含所有自变量的情况。

离散性概率分布函数较为直接，每个自变量的概率和即为对应的分布函数。

又叫“累计概率函数”。

概率密度函数：实质上指的是连续性随机变量的概率分布。

概率密度函数无法像离散型一样通过累计来求，但可通过积分来求。

由随机变量和对应的映射关系构成的函数曲线，可通过积分计算对应区间的面积。

所求的数据，表示了事件在该区间内所生的概率大小。

总结：概率分布函数和概率密度函数，无非是用来描述事件在某个点或者某个区间内发生的概率大小。

将其分为概率分布和概率密度函数，实质上是对连续性变量和离散型变量的分类讨论，特定数值，特定分析。

概率分布函数和概率密度函数的全区间的结果必都为1，即事件在全区间段内必会发生。

分布函数与概率密度函数解析：从数据到概率的映射关系在概率与统计学中，分布函数与概率密度函数是描述随机变量的重要工具。

它们提供了从数据到概率的映射关系，帮助我们理解和分析数据的概率分布特性。

本文将从数学角度对分布函数（Cumulative Distribution Function, CDF）和概率密度函数（Probability Density Function, PDF）进行解析，探讨它们之间的关系以及在实际应用中的重要性。

一、分布函数（CDF）的定义与性质分布函数是描述随机变量X的累积概率分布的函数，通常用F(x)表示，定义为随机变量小于等于x的概率，即：F(x) = P(X ≤ x)其中，P表示概率。

分布函数具有以下性质：1. 非减性：对于任意实数x₁和x₂，如果x₁ ≤ x₂，则F(x₁) ≤F(x₂)；2. 连续性：对于任意实数x，有lim⁡(x→+∞) F(x) = 1和lim⁡(x→-∞) F(x) = 0；3. 右连续性：对于任意实数x，有F(x) = F(x⁺)，其中x⁺表示x的右极限。

二、概率密度函数（PDF）的定义与性质概率密度函数是描述随机变量X的概率密度的函数，通常用f(x)表示，定义为随机变量落在无穷小区间[x, x + xx]内的概率除以该区间的长度xx，即：x(x) = x(x = x) = lim⁡(xx→x) x(x≤ x≤ x + xx)/xx其中，P表示概率。

概率密度函数具有以下性质：1. 非负性：对于任意实数x，有f(x) ≥ 0；2. 归一性：∫∞ ̶∞ x(x) d x = 1，表示概率的总和为1；3. 不可为负数：对于任意实数x，有P(x ≤ X ≤ x + xx) ≈ f(x)xx，其中xx为无穷小量；4. 概率计算公式：对于任意区间[a, b]，有x(a ≤ x≤ b) = ∫x ̶x x(x)d x。

三、CDF与PDF的关系CDF和PDF是描述同一随机变量的不同表示方式，它们之间存在以下关系：1. CDF为PDF的累积积分：对于任意实数x，有F(x) = ∫∞ ̶x x(x)d x；2. PDF为CDF的导数：对于任意实数x，有f(x) = dF(x)/dx；3. 互为相反操作：CDF对应的是随机变量小于等于x的概率，而PDF对应的是随机变量在x处的概率密度。

分布函数与概率密度函数解读：随机事件的概率分布特性随机事件的概率分布特性是概率论和数理统计中的重要概念，用于描述随机事件在不同取值上出现的概率情况。

其中，分布函数和概率密度函数是常用的描述概率分布的工具。

本文将解读分布函数和概率密度函数的含义和用途，进一步探讨随机事件的概率分布特性。

一、分布函数分布函数，又称累积分布函数，是用来描述一个随机变量X小于或等于某个给定值x的概率。

设X为某个随机事件，其分布函数为F(X)，表示为F(x) = P(X ≤ x)。

分布函数具有以下特性：1. 若随机变量X为连续型随机变量，则分布函数F(x)为连续的。

若X为离散型随机变量，则F(x)为右连续的，即在x点右侧的概率为F(x)。

2. 分布函数F(x)的取值范围为[0, 1]，且具有单调非减性质。

即当x₁ < x₂时，有F(x₁) ≤ F(x₂)。

3. F(x)是一个关于x的非降右连续函数，其导数为概率密度函数f(x)。

即f(x) = dF(x)/dx。

二、概率密度函数概率密度函数，简称密度函数，是用来描述连续型随机变量在某个取值上的概率密度。

设X为某个连续型随机变量，其概率密度函数为f(X)，表示为f(x) = dF(x)/dx。

概率密度函数具有以下特性：1. 概率密度函数f(x)是一个非负函数，且在整个实数轴上积分为1。

即∫f(x)dx = 1。

2. 由于概率密度函数只描述了连续型随机变量在某一点的概率密度，而非具体的概率值。

因此，通过密度函数计算某一点上的概率需借助于积分，即P(a ≤ X ≤ b) = ∫f(x)dx，其中a、b为区间。

三、分布函数与概率密度函数关系分布函数与概率密度函数是相辅相成的概念。

通过分布函数可以求得概率密度函数，通过概率密度函数可以求得分布函数。

1. 由分布函数求概率密度函数：设X为连续型随机变量，其分布函数F(x)在区间[a, b]可导，且其导数存在，则该导数即为该区间内的概率密度函数。

推导连续随机变量的分布函数与概率密度函数连续随机变量是概率论中的重要概念之一，通过分布函数和概率密度函数可以描述和推导连续随机变量的性质。

本文将就连续随机变量的分布函数和概率密度函数进行详细推导和说明。

一、连续随机变量的分布函数对于一个连续随机变量X，定义其分布函数为F(x)，即：F(x) = P(X ≤ x)，其中x为任意实数。

分布函数F(x)具有以下性质：1. F(x)是单调增加的函数；2. 0 ≤ F(x) ≤ 1，对于任意实数x；3. 当x → -∞时，F(x) → 0；4. 当x → +∞时，F(x) → 1。

接下来，我们通过对分布函数求导，可以得到连续随机变量的概率密度函数。

二、连续随机变量的概率密度函数定义连续随机变量X的分布函数为F(x)，则连续随机变量X的概率密度函数f(x)可以通过以下公式得到：f(x) = dF(x)/dx根据导数的定义，f(x)表示分布函数F(x)关于x的导数。

概率密度函数f(x)具有以下性质：1. f(x) ≥ 0，对于任意实数x；2. ∫[a,b] f(x)dx = P(a ≤ X ≤ b)，其中[a,b]表示区间[a,b]上的积分。

通过概率密度函数，我们可以计算出连续随机变量在某一区间内的概率。

三、假设X是一个连续随机变量，通过以下步骤可以推导得到其分布函数和概率密度函数：1. 确定X的分布函数F(x)；2. 对分布函数F(x)求导，得到概率密度函数f(x)。

需要注意的是，不同类型的连续随机变量拥有不同的分布函数和概率密度函数。

常见的连续随机变量包括均匀分布、正态分布、指数分布等。

以正态分布为例，其分布函数和概率密度函数分别为：分布函数：F(x) = (1/2)[1 + erf((x-μ)/(σ√2))]概率密度函数：f(x) = (1/σ√(2π)) * exp(-(x-μ)²/(2σ²))其中，μ为均值，σ为标准差，erf为误差函数。

分布函数与概率密度函数解析：概率密度函数的性质分析分布函数与概率密度函数是概率论中常用的两个概念，它们可以描述随机变量的分布特征与概率分布。

其中，概率密度函数是对连续型随机变量分布进行描述的函数，而分布函数则是概率密度函数的积分形式。

本文将对分布函数与概率密度函数的定义、性质及其在实际问题中的应用进行详细的解析和分析。

一、分布函数的定义与性质首先，我们来定义分布函数的概念。

对于一个随机变量X，它的分布函数F(x)定义为：F(x) = P(X ≤ x)，其中P表示概率。

分布函数具有以下几个性质：1. 范围性：分布函数的值域为[0, 1]。

2. 单调性：随着x的增大，分布函数递增。

3. 右连续性：分布函数在每个点x处均连续。

4. 左极限性：分布函数的左极限存在（可能等于或小于分布函数在该点的值）。

5. 概率性：当x趋于负无穷时，分布函数趋于0；当x趋于正无穷时，分布函数趋于1。

二、概率密度函数的定义与性质接下来，我们介绍概率密度函数的概念。

对于一个连续型随机变量X，它的概率密度函数f(x)定义为：f(x) = dF(x)/dx。

概率密度函数具有以下几个性质：1. 非负性：对于所有的实数x，概率密度函数的取值为非负数。

2. 归一性：概率密度函数的积分等于1，即∫f(x)dx = 1。

3. 概率性：对于任意实数a和b（a<b），随机变量X落在区间[a, b]内的概率为∫[a,b]f(x)dx。

概率密度函数与分布函数之间存在一种导数与积分的关系，即：F(x) = ∫[-∞, x]f(t)dt。

三、概率密度函数的性质分析概率密度函数在概率论和统计学中具有重要的应用价值。

下面，我们将对概率密度函数的一些相关性质进行进一步分析。

1. 概率密度函数的图像特征：概率密度函数的图像通常是一个连续曲线，且满足非负性和归一性。

在概率密度函数图像中，概率密度函数曲线下的面积表示随机变量落在对应区间内的概率。

2. 概率密度函数的峰值与分布类型：概率密度函数的峰值对应于概率密度函数图像上的最高点，它反映了随机变量的众数或最可能取到的值。

你对分布函数和概率密度函数的理解分布函数和概率密度函数是概率论与数理统计中重要的概念。

它们是描述随机变量取值分布情况的方法，是许多统计问题的基础。

本文将从以下几个方面介绍分布函数和概率密度函数的含义和应用。

一、分布函数的定义和性质分布函数是描述随机变量X不大于某个值x的概率的函数，通常记作F(x)，即F(x)=P(X≤x)。

其中，P表示概率。

分布函数具有以下性质：1、F(x)是一个单调不减函数，即对于任意的x1<x2，有F(x1)≤F(x2)。

2、F(x)的取值范围在[0,1]之间，即0≤F(x)≤1。

3、当x趋近于负无穷时，F(x)趋近于0；当x趋近于正无穷时，F(x)趋近于1。

二、概率密度函数的定义和性质概率密度函数是描述随机变量X在某个区间内取值的概率密度的函数，通常记作f(x)，即f(x)=dF(x)/dx。

其中，dF(x)表示F(x)的微分。

概率密度函数具有以下性质：1、f(x)是一个非负函数，即f(x)≥0。

2、概率密度函数的积分在全域内等于1，即∫f(x)dx=1。

3、概率密度函数与分布函数之间有以下关系：F(x)=∫f(t)dt，其中积分区间为(-∞, x]。

三、分布函数和概率密度函数的应用1、求概率分布函数和概率密度函数可以用来求随机变量X在某个区间内取值的概率。

如果已知概率密度函数f(x)，则可以根据积分公式求出分布函数F(x)，然后用F(x)的差值求出概率。

例如，求X在[0,1]区间内取值的概率，可以用P(X≤1)-P(X≤0)=F(1)-F(0)来计算。

2、求期望和方差分布函数和概率密度函数还可以用来求随机变量X的期望和方差。

期望是随机变量取值的平均值，可以用积分公式E(X)=∫xf(x)dx来计算。

方差是随机变量取值与期望之差的平方的期望，可以用积分公式Var(X)=E((X-E(X))^2)=∫(x-E(X))^2f(x)dx来计算。

3、拟合分布分布函数和概率密度函数还可以用来拟合实际数据的分布情况。

概率分布函数与概率密度函数概率分布函数与概率密度函数是概率论中两个重要的概念，用于描述和分析随机变量的概率分布特征。

本文将介绍概率分布函数（Probability Distribution Function，简称PDF）和概率密度函数（Probability Density Function，简称CDF）的定义与性质，并通过实例说明它们的应用。

一、概率分布函数（Probability Distribution Function）概率分布函数是描述随机变量取某个特定值的概率的函数。

其定义为随机变量X的分布函数，记作F(x)，即F(x) = P(X ≤ x)。

其中，P(X ≤ x)表示随机变量X小于等于x的概率。

概率分布函数具有以下性质：1. 对于任意的实数x，0 ≤ F(x) ≤ 1，即概率分布函数的取值范围在[0,1]之间。

2. F(x)是非降函数，即当x1 < x2时，有F(x1) ≤ F(x2)。

3. F(x)是右连续函数，即当x→x0+时，有F(x)→F(x0)。

概率分布函数的图像是一个递增且不断向上逼近1的曲线。

通过概率分布函数，可以计算出随机变量X在某个区间内的概率。

例如，对于连续型随机变量X，可以使用积分来求得区间概率，即P(a ≤ X ≤ b) = F(b) - F(a)。

二、概率密度函数（Probability Density Function）概率密度函数是描述连续型随机变量概率分布的函数。

其定义为随机变量X在一点x附近单位长度上的概率，记作f(x)。

即在微小的区间(dx)内，随机变量X取值在x附近的概率为f(x)dx。

概率密度函数具有以下性质：1. f(x) ≥ 0，即概率密度函数的取值非负。

2. 随机变量X在整个样本空间的概率等于1，即∫f(x)dx = 1。

概率密度函数描述了连续型随机变量的概率分布情况，其图像是一个连续的曲线。

通过概率密度函数，可以计算出随机变量X在某个特定取值处的概率密度。

如何理解概率分布函数和概率密度函数大学的时候，我的《概率论和数理统计》这门课一共挂过3次，而且我记得最后一次考过的时候刚刚及格，只有60分。

你可以想象我的《概率论》这门课学的是有多差了。

后来，我工作以后，在学习数据分析技能时，又重新把《概率论》这本书学了一遍。

原来之前一直没学好这门课的很重要一个原因就是，这门课涉及很多基础的概念，而我当初就是对这些概念非常不理解。

今天我就讲讲应该如何理解概率分布函数和概率密度函数的问题。

是不是乍一看特别像，容易迷糊。

如果你感到迷糊，恭喜你找到我当年的感觉了。

先从离散型随机变量和连续性随机变量说起对于如何分辨离散型随机变量和连续性随机变量，我这里先给大家举几个例子:1、一批电子元件的次品数目。

2、同样是一批电子元件，他们的寿命情况。

在第一个例子中，电子元件的次数是一个在现实中可以区分的值，我们用肉眼就能看出，这一堆元件里，次品的个数。

但是在第二个例子中，这个寿命它是一个你无法用肉眼数的过来的数字，它需要你用笔记下来，变成一个数字你才能感受它。

在这两个例子中，第一例子涉及的随机变量就是离散型随机变量，第二个涉及的变量就是连续型随机变量。

在贾俊平老师的《统计学》教材中，给出了这样的区分:如果随机变量的值可以都可以逐个列举出来，则为离散型随机变量。

如果随机变量X 的取值无法逐个列举则为连续型变量。

我始终觉得，贾老师这么说，对于我们这些脑子笨又爱钻牛角尖的学生来说，还是不太好理解。

所以我就告诉大家一个不一定非常严谨，但是绝对好区分的办法。

只要是能够用我们日常使用的量词可以度量的取值，比如次数，个数，块数等都是离散型随机变量。

只要无法用这些量词度量，且取值可以取到小数点2位，3位甚至无限多位的时候，那么这个变量就是连续型随机变量!对了，如果你连随机变量这个概念还不理解的话，我送你一句贾俊平老师的话:如果微积分是研究变量的数学，那么概率论与数理统计是研究随机变量的数学。

再来理解离散型随机变量的概率分布，概率函数和分布函数在理解概率分布函数和概率密度函数之前，我们先来看看概率分布和概率函数是咋回事。

你对分布函数和概率密度函数的理解分布函数与概率密度函数在概率论与数理统计中是两个非常重要的概念，它们分别用于描述随机变量的分布情况和概率密度分布情况。

在本文中，我们将对这两个概念进行详细的解释和分析。

一、分布函数分布函数又称累积分布函数，是描述随机变量取值情况的函数。

设随机变量X的分布函数为F(x)，其定义为：F(x)=P(X≤x)其中，P表示概率，X≤x表示随机变量X的取值小于或等于x的概率。

也就是说，对于任意一个实数x，F(x)表示随机变量X的取值小于或等于x的概率。

分布函数具有以下性质：1. F(x)是一个非降函数，即随着x的增大，F(x)不会减小。

2. F(x)的取值范围在0到1之间，即0≤F(x)≤1。

3. F(x)在x处的右导数为其密度函数f(x)，即F'(x)=f(x)。

二、概率密度函数概率密度函数是用于描述随机变量概率密度分布情况的函数。

设随机变量X的概率密度函数为f(x)，则对于任意一个实数x，其定义为：P(a<X<b)=∫abf(x)dx其中，a和b为实数，a<b，∫表示积分符号。

概率密度函数具有以下性质：1. f(x)是一个非负函数，即f(x)≥0。

2. f(x)的积分值为1，即∫∞−∞f(x)dx=1。

3. 在任意一个区间[a,b]内的概率为区间上的概率密度函数f(x)在该区间上的积分，即P(a<X<b)=∫abf(x)dx。

三、分布函数与概率密度函数的联系分布函数和概率密度函数是两个不同的概念，但它们之间存在着密切的联系。

具体来说，概率密度函数是分布函数的导数，而分布函数是概率密度函数的积分。

设随机变量X的概率密度函数为f(x)，分布函数为F(x)，则有：F(x)=P(X≤x)=∫−∞xf(t)dtf(x)=dF(x)/dx这个关系可以用于相互转换分布函数和概率密度函数。

在实际应用中，我们常常需要根据分布函数或概率密度函数计算概率或期望等统计量。

分布函数与概率密度函数解读：从概率到数据的转化过程概率论作为数学的一个分支，研究的是不确定性事件的数量化方法。

而分布函数与概率密度函数则是概率论中的两个重要概念，用于描述随机变量的特征和分布规律。

本文将从概率的角度，解读分布函数与概率密度函数，并探讨其在数据分析中的应用。

一、分布函数分布函数，又称累积分布函数（Cumulative Distribution Function，简称CDF），是用于描述随机变量取值在某一点或之前的累积概率的函数。

对于一个随机变量X，其分布函数FX(x)定义为：FX(x) = P(X ≤ x)其中，P(X ≤ x)表示X小于等于x的概率。

分布函数具有以下几个特点：1. FX(x)的值域是[0, 1]，因为概率的取值范围在0到1之间；2. FX(x)是非递减函数，即随着x的增加，FX(x)的值不会减小；3. FX(x)是右连续的，即对于任意x0，有FX(x0+) = FX(x0)，其中x0+表示x0的右极限。

二、概率密度函数概率密度函数，简称密度函数（Probability Density Function，简称PDF），是用于描述连续型随机变量概率分布的函数。

对于一个随机变量X，其概率密度函数fX(x)定义为：fX(x) = d(FX(x))/dx其中，d(FX(x))/dx表示FX(x)的导数。

概率密度函数具有以下几个特点：1. 概率密度函数的值在某个区间上的积分，即∫fX(x)dx，表示该随机变量的累积概率；2. 概率密度函数的非负性，即fX(x) ≥ 0，因为概率不能为负数；3. 概率密度函数的归一性，即∫fX(x)dx = 1，表示概率的总和为1。

三、从分布函数到概率密度函数分布函数与概率密度函数之间存在紧密的联系，它们通过求导/积分的方式相互转化。

对于一个连续型随机变量X，如果它的分布函数FX(x)可导，并且对于任意x，都有d(FX(x))/dx = fX(x)，则称其具有概率密度函数。

分布函数与概率密度函数分析：概率密度曲线的形状解析概率密度函数（Probability Density Function，PDF）和分布函数（Cumulative Distribution Function，CDF）是统计学中常用的概率描述工具。

本文将通过分析概率密度曲线的形状来揭示PDF和CDF之间的关系，并探讨其在实际应用中的意义。

一、概率密度函数与分布函数的概念及定义概率密度函数是指对于连续型随机变量X，定义域内任意取到的值x，其概率密度函数f(x)满足以下两个条件：1. f(x)大于等于零，即f(x)≥0。

2. 在定义域上的所有值的累积概率等于1，即∫f(x)dx=1。

分布函数是指对于连续型随机变量X，在实数轴上定义域内任意取到的值x，其分布函数F(x)满足以下两个条件：1. F(x)大于等于零，即F(x)≥0。

2. F(x)为非递减函数，即对于任意x1<x2，有F(x1)≤F(x2)。

二、概率密度曲线的形状解析概率密度曲线是描述连续型随机变量概率分布的图形。

根据概率密度函数的定义，我们可以得到概率密度曲线的性质：1. 概率密度曲线位于x轴上方，且不与x轴相交。

2. 概率密度曲线下的面积等于对应区域内的累积概率。

3. 曲线的高度反映了该取值的概率密度大小。

根据不同的概率密度函数形状，概率密度曲线也会呈现不同的形态。

以下将介绍三种常见的概率密度曲线形态：1. 正态分布正态分布是指符合高斯分布特性的概率密度函数形态。

其概率密度曲线为钟形曲线，左右对称，呈现单峰形态。

正态分布在自然界和社会现象中广泛存在，例如身高、体重等具有集中趋势的数据往往服从正态分布。

2. 均匀分布均匀分布是指概率密度函数在定义域上几乎处处相等的分布。

其概率密度曲线为矩形，高度恒定。

均匀分布常用于随机抽样、数值模拟等领域。

3. 指数分布指数分布是指概率密度函数呈指数型下降的分布。

其概率密度曲线在图像上呈现单调递减的曲线形状。

概率及概率密度分布函数概率及概率密度分布函数是概率论中的重要概念，用于描述随机变量的分布情况。

概率研究的是随机事件的可能性，而概率密度分布函数则描述了连续型随机变量在某个取值范围内的概率密度。

一、概率的基本概念概率在概率论中是指某个事件发生的可能性大小。

常用的概率表示方法有百分数、分数和小数等形式。

如果某个事件必然发生，则其概率为1；如果某个事件不可能发生，则其概率为0。

对于其他事件，其概率一般介于0和1之间。

二、概率的计算方法根据概率的定义，我们可以通过实验来确定某个事件发生的概率。

在实验中，若某事件发生的次数为m，总共进行实验的次数为n，则该事件发生的概率可用频率表示为m/n。

此外，还有一些常用的概率计算方法，如加法定理、乘法定理、条件概率等。

加法定理适用于求两个事件中至少一个发生的概率；乘法定理适用于求两个相继独立事件同时发生的概率；条件概率则描述了在已知某事件发生的情况下，另一个事件发生的概率。

三、概率密度分布函数概率密度分布函数是用来描述连续型随机变量的分布情况的数学函数。

对于一个连续型随机变量X，其概率密度函数f(x)定义为在x处的概率密度。

一般来说，概率密度函数为非负的连续函数，并满足积分为1的条件。

在实际应用中，概率密度分布函数可以用图像形式表示出来，常用的图像表示方法有直方图、正态分布曲线等。

直方图可以直观地反映出某一区间内的事件发生的概率密度，而正态分布曲线则是一种常见的连续概率分布曲线。

四、概率密度分布函数的应用概率密度分布函数在概率统计学中有着广泛的应用。

它可以用于描述各种现实世界的随机现象，如人类身高、体重的分布，机器零件的寿命，气象数据等。

通过分析概率密度分布函数，我们可以得到关于随机变量的各种统计量，如期望、方差、标准差等。

这些统计量能够帮助我们对随机变量的分布特征进行全面的描述和分析。

总结：概率及概率密度分布函数是概率论中重要的概念，用于描述随机变量的分布情况。

概率是指某个事件发生的可能性大小，可以通过实验或计算得到。