20.2.1中位数和众数1

华师大版八下数学20.2《数据的集中趋势》20.2.1中位数和众数说课稿一. 教材分析华师大版八下数学20.2《数据的集中趋势》20.2.1中位数和众数是学生在学习了平均数、方差等统计量之后，进一步研究数据集中趋势的内容。

本节内容通过中位数和众数的定义和性质，让学生了解并掌握它们在描述数据集中趋势方面的作用，以及如何运用中位数和众数解决实际问题。

教材通过丰富的例题和练习，引导学生探究中位数和众数的特点，培养学生的数据分析能力。

二. 学情分析学生在学习本节内容前，已经掌握了平均数、方差等统计量的概念和方法，具备了一定的数据分析基础。

但中位数和众数与平均数有所不同，它们不受极端数据的影响，能更好地反映数据的一般水平。

学生在学习过程中，需要理解中位数和众数的意义，掌握它们的求法，并能够运用它们解决实际问题。

三. 说教学目标1.知识与技能：理解中位数和众数的定义，掌握求中位数和众数的方法，能正确运用它们描述数据集中趋势。

2.过程与方法：通过实例分析，培养学生收集、整理、处理数据的能力，提高数据分析水平。

3.情感态度与价值观：培养学生对数据的敏感性，培养学生的团队协作精神，使学生在解决实际问题中，能够充分利用数据信息。

四. 说教学重难点1.重点：中位数和众数的定义、性质和求法。

2.难点：理解中位数和众数在描述数据集中趋势方面的作用，以及如何运用它们解决实际问题。

五. 说教学方法与手段1.教学方法：采用问题驱动法、案例分析法、小组讨论法等，引导学生主动探究、合作学习。

2.教学手段：利用多媒体课件、实物投影、板书等，辅助教学，提高教学效果。

六. 说教学过程1.导入：通过一组数据，引导学生思考：如何描述这组数据的集中趋势？激发学生的学习兴趣，引出本节课的内容。

2.讲解：介绍中位数和众数的定义，通过实例讲解它们的求法，让学生理解中位数和众数在描述数据集中趋势方面的作用。

3.练习：让学生分组讨论，分析一组数据的中位数和众数，培养学生的数据分析能力。

第二十章数据的分析20.1数据的代表20.1.1平均数（第一课时）一、教学目标：1、使学生理解数据的权和加权平均数的概念2、使学生掌握加权平均数的计算方法3、通过本节课的学习，还应使学生理解平均数在数据统计中的意义和作用：描述一组数据集中趋势的特征数字，是反映一组数据平均水平的特征数。

二、重点、难点和难点突破的方法：1、重点：会求加权平均数2、难点：对“权”的理解1、加深对加权平均数的理解2、会根据频数分布表求加权平均数，从而解决一些实际问题3、会用计算器求加权平均数的值第二十章数据的分析课题20.1 数据的代表课时：六课时第一课时20.1.1 平均数【学习目标】1、使学生理解数据的权和加权平均数的概念2、使学生掌握加权平均数的计算方法3、通过本节课的学习，还应使学生理解平均数在数据统计中的意义和作用：描述一组数据集中趋势的特征数字，是反映一组数据平均水平的特征数。

【重点难点】重点：会求加权平均数难点：对“权”的理解【导学指导】学习教材P124－P127相关内容，思考、讨论、合作交流后完成下列问题：1．你认为P124“思考”中小明的做法有道理吗？为什么?2．正确的解法应是怎样的？请谈谈你的看法。

3．什么是加权平均数？4．P125“例1”中，所求的结果已不再是各人听说读写成绩的简单平均，而是听说读写成绩的加权平均数，它们的权分别是多少？5．P126“例2”中，两名选手的单项成绩都是两个95分与一个85分，为什么他们的最后得分不同呢？谈谈你对权的作用的体会。

【课堂练习】1．教材P127练习第1,2题。

2、在一个样本中，2出现了x1次，3出现了x2次，4出现了x3次，5出现了x4次，则这个样本的平均数为.3、某人打靶，有a次打中x环，b次打中y环，则这个人平均每次中靶环。

4、一家公司打算招聘一名部门经理，现对甲、乙两名应聘者从笔试、面试、实习成绩三个方面表现进行评分，笔试占总成绩20%、面试占30%、实习成绩占50%，各项成绩如表所示：试判断谁会被公司录取，为什么？5、在一次英语口试中，已知50分1人、60分2人、70分5人、90分5人、100分1人，其余为84分。

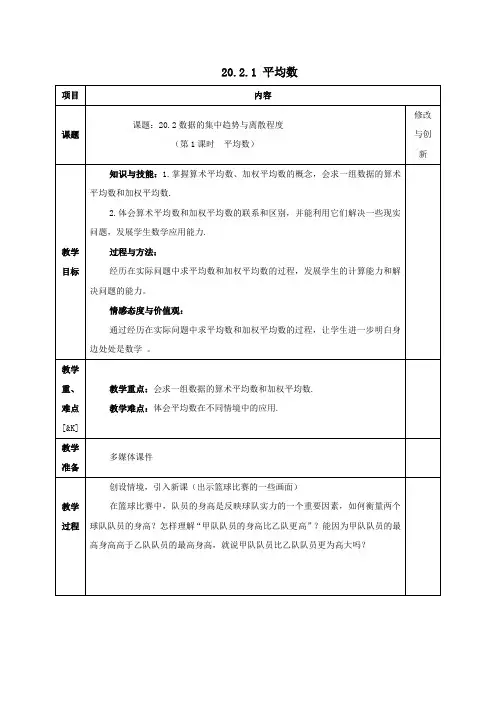
20.2.1 平均数上面两支球队中，哪支球队队员的身材更为高大？哪支球队队员更为年轻？你是怎样判断的？活动1：前后桌四人交流.找同学回答后，给出算术平均数的定义.一般地，对于n 个数x 1，x 2，…，x n ，我们把叫做这n 个数的算术平均数，简称平均数，记为x .读作“x 拔”.活动2：请同学们结合图表，自己用计算器算出各球队的平均身高和平均年龄，看哪一个球队的平均身高高？哪一个球队的平均年龄小？想一想：小明是这样计算东方大鲨鱼队的平均年龄的：年龄/岁 16 18 21 23 24 26 29 34相应队员人数 1 2 4 1 3 1 2 1平均年龄＝（16×1＋18×2＋21×4＋23×1＋24×3＋26×1＋29×2＋34×1）÷（1＋2＋4＋1＋3＋1＋2＋1）≈23.3（岁）.()n x x x n++Λ21120.2.2中位数与众数20.2.3 数据的离散程度【通过展示图形，学生可以通过图表做出正确的判断，即机床B 做出的零件精度明显高于机床A 。

此时，教师提出问题：能否从数量上对上述结果做出准确判断？这个问题的提出，既暗示了学生探究的可持续性，又促进了学生的进一步思考。

】提问：能否用数量来刻画一组数据的离散情况呢？3．（1）不难从表格中看出，机床A 的数据明显比机床B 的数据较为分散，因此，引导学生计算两组数据中各个数据与标准数据20.0的差，继而计算偏差和i x x -，并继续填入表格，尝试能否解决问题：平均数中位数极差 偏差和机床A 20.0 20.0 0.4 0 机床B20.020.00.4【学生通过计算，发现偏差和并不能顺利解决问题.与学生共同分析发现：要想准确回答问题，我们仅仅需要知道两组中的各个数据与标准尺寸的相对偏差大小，至于到底是大于标准尺寸，还是小于标准尺寸，并不是关心的主要对象。

华师大版八下数学20.2《数据的集中趋势》20.2.1中位数和众数教学设计一. 教材分析华师大版八下数学20.2《数据的集中趋势》20.2.1中位数和众数是研究数据集中趋势的重要内容。

本节内容通过引入中位数和众数的概念，让学生了解并掌握数据的一种描述方法，从而能够更好地理解数据的特征。

教材通过丰富的实例和生动的语言，引导学生探究中位数和众数的求法及其应用，为学生提供了一种分析数据的新视角。

二. 学情分析学生在学习本节内容前，已初步掌握了平均数的概念，能理解数据有高低之分，但对于数据集中趋势的认识尚浅。

此外，学生对于中位数和众数的实际应用可能较为陌生，因此需要通过实例分析来引导学生理解和掌握。

三. 教学目标1.了解中位数和众数的概念，掌握它们的求法。

2.能够运用中位数和众数分析数据的集中趋势，解决实际问题。

3.培养学生的数据分析能力，提高学生解决实际问题的能力。

四. 教学重难点1.重点：中位数和众数的定义，求法及应用。

2.难点：理解中位数和众数在数据分析中的作用，能够灵活运用。

五. 教学方法1.情境教学法：通过生活实例引入中位数和众数的概念，让学生在具体的情境中感受和理解。

2.问题驱动法：设置问题引导学生探究中位数和众数的求法，激发学生的思考。

3.合作学习法：分组讨论，让学生在合作中交流，共同解决问题。

六. 教学准备1.准备相关的生活实例和数据，用于引导学生探究。

2.制作课件，展示中位数和众数的求法及应用。

3.准备练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）通过一个班级成绩单的生活实例，引导学生关注数据的集中趋势，提出问题：“如果你是这个班的老师，你想知道这个班学生的成绩集中在哪里？”从而引出中位数和众数的概念。

2.呈现（10分钟）讲解中位数和众数的定义，通过具体的数据实例，让学生理解中位数和众数的求法。

3.操练（10分钟）让学生分组讨论，每组选取一组数据，求出中位数和众数，并解释其含义。

20.2.1　中位数和众数知识点1　中位数1.某校篮球队五名主力队员的身高分别是173,180,181,176,178(单位: cm),将这些数据按从小到大的顺序排列为 ,因为数据的个数是奇数,所以这五名运动员身高的中位数是 .2.一组数据1,3,3,4,4,5的中位数是( )A.3B.3.5C.4和3D.43.学习全等三角形时,某班举行了以“生活中的全等”为主题的测试活动,全班学生的测试成绩统计如下表:得分(分)85899396100人数(人)4615132则这些学生得分的中位数是( )A.89分B.91分C.93分D.96分4.某中学八年级(2)班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个):35　38　42　44　40　47　45　45则这组数据的中位数、平均数分别是( )A.42,42B.43,42C.43,43D.44,435.生命在于运动.运动渗透在生命中的每一个角落,运动的好处就在于让我们的身体保持健康的状态.小明同学用手机软件记录了自己11月份每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在小明每天所走的步数数据中,中位数是 万步.6.一名射击运动员在连续射靶时,2次射中10环,8次射中9环,7次射中8环,2次射中7环,1次射中6环,求这组成绩的平均数和中位数.知识点2　众数7.在某次体育测试中,八年级(1)班5名同学的立定跳远成绩(单位:m)分别为:1.81,1.98,2.10,2.30,2.10.在这组数据中, 出现2次,出现的次数最多,所以这组数据的众数为 .8. 据了解,某定点医院收治的7名新型冠状肺炎患者的新冠病毒潜伏期分别为2天、3天、3天、4天、4天、4天、7天,则这7名患者新冠病毒潜伏期的众数和中位数分别为( ) A.4天,4天B.3天,4天C.4天,3天D.3天,7天9. 在某时段有50辆车通过一个雷达测速点,工作人员将测得的车速绘制成如图所示的条形统计图,则这50辆车的车速的众数(单位: km/h)为( )A.60B.50C.40D.1510.受央视《朗读者》节目的影响,某校八年级(2)班近期准备组织一次朗诵活动,语文老师调查了全班学生平均每天的阅读时间,统计结果如下表所示:每天阅读时间(h)0.511.52人数89103则在本次调查中,全班学生平均每天阅读时间的中位数和众数分别是( )A.2 h,1 hB.1 h,1.5 hC.1 h,2 hD.1 h,1 h11.一组数据1,3,2,7,x,2,3的平均数是3,则该组数据的众数为 .12.某校八年级(1)班全体学生2020年初中毕业体育考试的成绩统计如下表:成绩(分)35394244454850人数(人)2566876根据上表中的信息判断下列结论错误的是( )A.该班一共有40名同学B.该班学生这次考试成绩的众数是45分C.该班学生这次考试成绩的中位数是45分D.该班学生这次考试成绩的平均数是45分13. 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示,这些成绩的中位数和众数分别是( )A.96分,98分B.97分,98分C.98分,96分D.97分,96分14.某班7个兴趣小组的人数如下:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是( )A.6B.6.5C.7D.815.已知一组数据4,3,2,m,n的众数为3,平均数为2,m>n,则n的值为 .16.已知数据a1,a2,a3,a4,a5的平均数是m,且a1>a2>a3>a4>a5>0,则数据a1,a2,a3,-3,a4,a5的平均数和中位数分别是 .17.某商场购进600箱苹果.在出售之前,先从中随机抽出10箱检查,称得10箱苹果的质量(单位:千克)如下:5.0,5.4,4.4,5.3,5.0,5.0,4.8,4.8,4.0,5.3.(1)请指出这10箱苹果质量的平均数、中位数和众数分别是多少;(2)请你根据上述结果估计600箱苹果的质量为多少千克.18.我国是世界上严重缺水的国家之一.为了倡导“节约用水,从我做起”,小刚从他所在班的50名同学中,随机调查了10名同学一年中的家庭月平均用水量(单位:t),并将调查结果绘成了条形统计图(1)求这10名同学的家庭月平均用水量的平均数、众数和中位数;(2)试估计小刚所在班的50名同学的家庭月平均用水量不超过7 t的有多少户.参考答案1.173,176,178,180,181　178 cm2.B　[解析] 按从小到大的顺序排列此组数据为1,3,3,4,4,5,处于中间位置的数是3,4,所以这组数据的中位数是(3+4)÷2=3.5.故选B.3.C　[解析] 处于中间位置的数为第20,21两个数,都为93分,所以中位数为93分.故选C.4.B　[解析] 把这组数据按从小到大的顺序排列得35,38,40,42,44,45,45,47,则这组数据的中位数为=43.=(35+38+42+44+40+47+45+45)=42.故选B.5.1.3　[解析] ∵共有2+8+7+10+3=30(个)数据,∴这组数据的中位数是第15,16个数据的平均数,而第15,16个数据均为1.3万步,则中位数是1.3万步.故答案为1.3.6.解:这组成绩的平均数为(10×2+9×8+8×7+7×2+6×1)÷(2+8+7+2+1)=8.4(环),中位数为=8.5(环).7.2.10　2.108.A9.C　[解析] 由条形图知,40出现的次数最多.故选C.10.B11.3　[解析] 根据题意知=3,解得x=3,则这组数据为1,2,2,3,3,3,7,所以众数为3.故答案为3.12.D13.A　[解析] 由统计图可知:按从小到大的顺序排列,第13名同学的分数为96分,故中位数为96分,得分人数最多的是98分,共9人,故众数为98分.故选A.14.C　[解析] 根据题意,得=7,解得x=8,∴这组数据的中位数是7.故选C.15.-2　[解析] ∵一组数据4,3,2,m,n的众数为3,平均数为2,m>n,∴m=3,∴4+3+2+3+n=2×5,解得n=-2.故答案为-2.16.,　[解析] ∵数据a1,a2,a3,a4,a5的平均数是m,∴a1+a2+a3+a4+a5=5m,∴数据a1,a2,a3,-3,a4,a5的平均数为(a1+a2+a3-3+a4+a5)÷6=.数据a1,a2,a3,-3,a4,a5按照从小到大的顺序排列为:-3,a5,a4,a3,a2,a1.处在第3,4位的数据的平均数为,∴数据a1,a2,a3,-3,a4,a5的中位数为.故答案为,.17.解:(1)平均数=(5.0+5.4+4.4+5.3+5.0+5.0+4.8+4.8+4.0+5.3)÷10=4.9(千克).因为5.0出现的次数最多,出现了3次,所以众数是5.0千克.将这10个数按从小到大的顺序排列为:4.0,4.4,4.8,4.8,5.0,5.0,5.0,5.3,5.3,5.4,因为第5个数与第6个数的平均数是5.0,所以这10箱苹果质量的中位数是5.0千克.(2)由(1)得平均每箱苹果的质量为4.9千克,所以估计600箱苹果的质量为4.9×600=2940(千克).18.解:(1)观察条形统计图,可知10名同学的家庭月平均用水量的平均数是(6×2+6.5×4+7×1+7.5×2+8×1)÷10=6.8(t).∵在这组数据中,6.5 t出现了4次,出现的次数最多,∴这10名同学的家庭月平均用水量的众数是6.5 t.∵将这组数据按从小到大的顺序排列,其中处于中间位置的两个数都是6.5 t,则=6.5(t),∴这10名同学的家庭月平均用水量的中位数是6.5 t.(2)∵10名同学的家庭中月平均用水量不超过7 t的有7户,∴小刚所在班的50名同学的家庭月平均用水量不超过7 t的有50×=35(户).。

华师大版八下数学20.2.2《平均数、中位数和众数的选用》说课稿2一. 教材分析华师大版八下数学20.2.2《平均数、中位数和众数的选用》这一节主要介绍了平均数、中位数和众数的概念及其应用。

平均数、中位数和众数是统计学中的基本概念，它们分别代表了数据的一种平均水平、集中趋势和典型值。

在实际生活中，这三种统计量广泛应用于各种领域，如教育、经济、社会等。

通过本节课的学习，使学生能够理解并掌握平均数、中位数和众数的定义及计算方法，能够根据实际情况选择合适的统计量，为解决实际问题提供依据。

二. 学情分析八年级的学生已经初步学习了实数、代数式等基础知识，具备一定的逻辑思维和分析问题的能力。

但学生在学习过程中，对平均数、中位数和众数的概念和应用可能还存在一定的困惑。

因此，在教学过程中，需要关注学生的认知水平，引导学生通过观察、思考、讨论等方式，深入理解这三种统计量的含义和作用。

三. 说教学目标1.知识与技能目标：理解平均数、中位数和众数的定义，掌握它们的计算方法，能够根据实际情况选择合适的统计量。

2.过程与方法目标：通过观察、分析、讨论等方法，培养学生的逻辑思维和数据分析能力。

3.情感态度与价值观目标：激发学生对数学学科的兴趣，培养学生运用数学知识解决实际问题的意识。

四. 说教学重难点1.教学重点：平均数、中位数和众数的定义及其计算方法。

2.教学难点：如何根据实际情况选择合适的统计量。

五. 说教学方法与手段1.教学方法：采用问题驱动、案例分析、小组讨论等教学方法，引导学生主动参与课堂，提高学生的学习兴趣和积极性。

2.教学手段：利用多媒体课件、实物模型、统计图表等教学辅助手段，帮助学生形象直观地理解平均数、中位数和众数的概念及应用。

六. 说教学过程1.导入新课：通过一个实际问题，引发学生对平均数、中位数和众数的思考，激发学生的学习兴趣。

2.概念讲解：讲解平均数、中位数和众数的定义，并通过例题展示它们的计算方法。

20.1.2中位数和众数（1）教学内容和地位：中位数是描述一组数据的集中趋势的统计特征量，是帮助学生学会用数据说话的基本概念。

本节课的教学内容和现实生活密切相关，是培养学生应用数学意识和创新能力的最好素材。

教学重点和难点：本节课的重点是中位数概念的形成过程及概念的运用。

本节课的难点是对统计数据从多角度进行全面地分析。

因为利用数据进行分析，对刚刚接触统计的学生来说，他们原有的认知结构中缺乏这方面的知识经验，所以，我们可以借助生活中的事例，利用丰富多彩的多媒体辅助，帮助学生突破这一知识难点。

教学目标分析：认知目标：（1）使学生认知中位数的意义；（2）会求一组数据的中位数。

能力目标：（1）让学生接触并解决一些社会生活中的问题，为学生创新学数学、用数学的情境，培养学生的数学应用意识和创新意识。

（2）在问题解决的过程中，培养学生的自主学习能力；（3）在问题分析的过程中，培养学生的团结协作精神。

情感目标：（1）通过多媒体网络课件，提供适当的问题情境，激发学生的学习热情，培养学生学习数学的兴趣；（2）在合作学习中，学会交流，相互评价，提高学生的合作意识与能力。

教学辅助：多媒体辅助教学课件.教法与学法：根据本节课的教学内容，主要采用了讨论发现法。

即课堂上，教师（或学生）提出适当的问题，通过学生与学生（或教师）之间相互交流，相互学习，相互讨论，在问题解决的过程中发现概念的产生过程，体现“数学教学是数学思维活动的过程的教学”。

在教学活动中，通过学生的自主学习来体现他们的主体地位，而教师是通过对学生参与学习的启发、调整、激励来体现自己的主导作用。

另外，在学生合作学习的同时，始终坚持对学生进行“学疑结合”、“学思结合”、“学用结合”的学法指导，这对学生的主体意识的培养和创新能力的培养都有积极的意义。

教学过程：1．创设情境，提出问题：[引入]首先我们一起看生活中的一个故事。

（多媒体网络课件通过网络广播演示）[内容]王老板有一个工厂，管理人员有王老板、6个亲戚；工作人员有5个领工、10个工人和1名徒。

20.1.2中位数和众数（1）
学习目标
知识与技能目标
（1）在具体情境中认识中位数，并会求出一组数据的中位数。

（2）理解中位数的作用，它们也是数据代表，可以反映一定的数据信息，帮助人们在实际问题中分析并做出决策。

（3）会利用中位数分析数据信息做出决策。

过程与方法目标
经历探索常见的数据集中趋势的特征数（中位数）的过程，感受中位数和平均数在实际应用中的作用，掌握判断方法，全程经历运用中位数进行数据分析与决策。

情感、态度与价值观目标
培养数据信息素养，体会数据的集中趋势的特征数的实际应用价值。

教学重点.难点
教学重点：
认识中位数这两种数据代表。

教学难点：
数据较多的利用中位数分析数据信息做出决策。

教法设计与学法指导
教法选择
针对八年级学生的认知结构和心理特征，为了突出重点，突破难点，本课题的教学坚持“教与学、知识与能力的辩证统一”和“使每个学生都得到充分发展”的原则，以“自主学习，同伴互助”教学法为主，辅之直观演示、讨论交流，让学生动脑思考，动口交流，动心关注。

学法指导
本节课注重调动学生积极思考、主动探索，尽可能地增加学生参与数学活动的时间和空间。

通过本课的教学，在教师的组织引导下，以学生自主学习为主，尝试学习、探究学习、合作交流学习相结合。

学习环境与资源设计
学习环境：运用多媒体课件。

学习资源：课本、教学课件（多媒体课件）、学生已有的生活经验等。

学具准备：常规学具准备。

教学流程安排
教学过程设计。

华师大版八下数学20.2《数据的集中趋势》20.2.2平均数、中位数和众数的选用说课稿3一. 教材分析华师大版八下数学20.2《数据的集中趋势》20.2.2平均数、中位数和众数的选用，是对平均数、中位数和众数概念的进一步深化。

本节内容通过实例讲解，让学生理解平均数、中位数和众数在实际问题中的应用，学会根据数据的特点选择合适的集中趋势量。

教材内容丰富，既有理论知识，又有实际应用，有利于培养学生的数学素养和解决问题的能力。

二. 学情分析学生在学习本节内容前，已经掌握了平均数、中位数和众数的概念，但对它们在实际问题中的应用还不够了解。

此外，学生可能存在对数据处理方法的困惑，不知道如何根据数据特点选择合适的集中趋势量。

因此，在教学过程中，教师需要引导学生运用已学知识解决实际问题，提高学生的数据处理能力。

三. 说教学目标1.知识与技能：让学生理解平均数、中位数和众数在实际问题中的应用，学会根据数据的特点选择合适的集中趋势量。

2.过程与方法：通过实例分析，培养学生运用数学知识解决实际问题的能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的团队协作能力和创新精神。

四. 说教学重难点1.重点：平均数、中位数和众数在实际问题中的应用，以及根据数据特点选择合适的集中趋势量。

2.难点：如何引导学生运用已学知识解决实际问题，提高数据处理能力。

五. 说教学方法与手段1.教学方法：采用问题驱动法、案例教学法和小组讨论法，引导学生主动探究、合作学习。

2.教学手段：利用多媒体课件、实物道具和统计软件，辅助教学，提高学生的学习兴趣和效果。

六. 说教学过程1.导入：通过一个具体实例，引出本节内容，激发学生的学习兴趣。

2.理论讲解：讲解平均数、中位数和众数的概念，以及它们在实际问题中的应用。

3.实例分析：分析实际问题，引导学生运用平均数、中位数和众数解决数据处理问题。

4.小组讨论：让学生分组讨论，总结平均数、中位数和众数的选用原则。