北师大版初三上数学相似三角形(一)

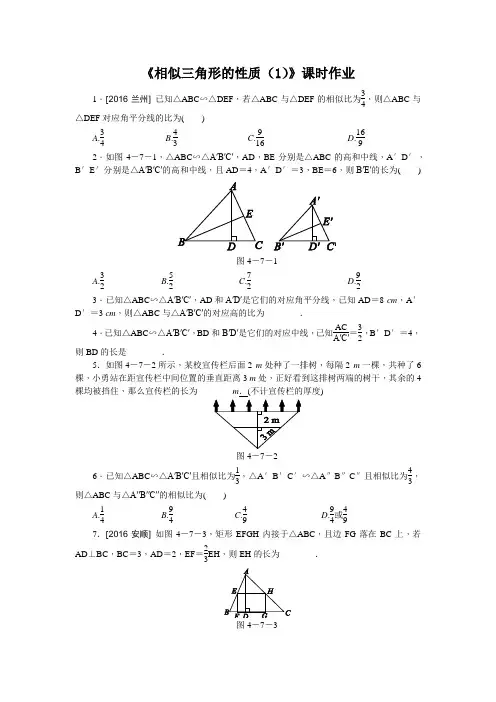
《相似三角形的性质（1）》课时作业1．[2016·兰州] 已知△ABC ∽△DEF ，若△ABC 与△DEF 的相似比为34，则△ABC 与△DEF 对应角平分线的比为( )A .34B .43C .916D .1692．如图4－7－1，△ABC ∽△A′B′C′，AD ，BE 分别是△ABC 的高和中线，A ′D ′，B ′E ′分别是△A′B′C′的高和中线，且AD ＝4，A ′D ′＝3，BE ＝6，则B′E′的长为( )图4－7－1A .32B .52C .72D .923．已知△ABC ∽△A′B′C′，AD 和A′D′是它们的对应角平分线，已知AD ＝8 cm ，A ′D ′＝3 cm ，则△ABC 与△A′B′C′的对应高的比为________．4．已知△ABC ∽△A′B′C′，BD 和B′D′是它们的对应中线，已知AC A′C′＝32，B ′D ′＝4，则BD 的长是________．5．如图4－7－2所示，某校宣传栏后面2 m 处种了一排树，每隔2 m 一棵，共种了6棵，小勇站在距宣传栏中间位置的垂直距离3 m 处，正好看到这排树两端的树干，其余的4棵均被挡住，那么宣传栏的长为________m ．(不计宣传栏的厚度)图4－7－26．已知△ABC ∽△A′B′C′且相似比为13，△A ′B ′C ′∽△A ″B ″C ″且相似比为43，则△ABC 与△A″B″C″的相似比为( )A .14B .94C .49D .94或497．[2016·安顺] 如图4－7－3，矩形EFGH 内接于△ABC ，且边FG 落在BC 上，若AD ⊥BC ，BC ＝3，AD ＝2，EF ＝23EH ，则EH 的长为________．图4－7－38．如图4－7－4是一个照相机成像的示意图，如果底片AB 宽40 mm ，焦距是60 mm ，求所拍摄的2 m 外景物的宽CD.图4－7－49．某高中学校为高一新生设计的学生板凳的正面视图如图4－7－5所示．其中BA ＝CD ，BC ＝20 cm ，BC ，EF 平行于地面AD 且到地面AD 的距离分别为40 cm ，8 cm ，为使板凳两腿底端A ，D 之间的距离为50 cm ，那么横梁EF 应为多长？(材质及其厚度等暂忽略不计)图4－7－510．如图4－7－6，△ABC 是一张锐角三角形的硬纸片，AD 是边BC 上的高，BC ＝40 cm ，AD ＝30 cm ，从这张硬纸片上剪下一个长HG 是宽HE 的2倍的矩形EFGH ，使它的一边EF 在BC 上，顶点G ，H 分别在AC ，AB 上，AD 与HG 的交点为M.(1)求证：AM AD ＝HG BC； (2)求矩形EFGH 的周长．图4－7－611．如图4－7－7所示，有一侦察员在距敌方200 m 的地方A 处发现敌人的一座建筑物DE ，但不知其高度，又不能靠近建筑物测量，机灵的侦察员将食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好能将建筑物遮住．若此时眼睛到食指的距离约为40 cm ，食指的长约为8 cm ，你能根据上述条件计算出敌方建筑物DE 的高度吗？请写出你的推理过程．图4－7－712．一块直角三角板的一条直角边AB的长为1.5 m，面积为1.5 m2，要把它加工成一个面积尽可能大的正方形桌面，甲、乙两位同学的加工方法如图4－7－8(1)(2)所示，请你用学过的知识说明哪位同学的加工方法更好．(加工损耗忽略不计，计算结果中的分数可保留)图4－7－8。

三角形相似判定方法的汇总及选用一.相似三角形的判定方法:(1)定义法:对应角相等,对应边的比相等的两个三角形相似.(2)平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.(3)判定定理1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.(4)判定定理2:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.(5)判定定理3:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.注意:①在两个三角形中，只要满足两个角对应相等,那么这两个三角形相似,证明时,关键是寻找对应角;②一般地,公共角、对顶角、同角的余角(或补角)都是相等的，在证明过程中要特别注意，这一判定方法是三角形相似的最常用的方法.二.合理选择判定方法在运用相似三角形的判定定理解几何问题时，要注意定理的选择，即①已知有一角相等时，可选择判定定理2 或判定定理3；②已知有两边的比相等时，可选择判定定理1或判定定理2.还应注意形似三角形判定定理的作用，即①可以用来判定两个三角形相似；②间接证明角相等，线段成比例：间接地为计算线段长度及角的大小创造条件.例1：如图1，点D 在△ABC 的边AB 上，满足怎样的条件时，△ACD ∽△ABC ？试分别加以举例.分析：此题属于探索性问题，由相似三角形的判定方法可知：△ACD 与△ABC 已有公共角∠A,要使这两个三角形相似，可根据相似三角形的判定方法寻找一个条件即可.解：当满足以下三个条件之一时，△ACD ∽△ABC.条件一：∠ACD=∠B;条件二：∠ADC=∠ACB; 条件三：,ABAC AC AD =.2AB AD AC ⋅= 反思：本题探索的问题是相似三角形的判别方法，在探索两个三角形形似时，用分析法，可先证明△ACD ∽△ABC 然后寻找两个三角形中边的关系或角的关系即可.例2:如图2,已知△ABC 中,,900=∠C D 、E 在BC 上，且BD=DE=EC=AC ，指出图中相似三角形,并证明你的结论.分析:先利用排除法找到不可能形似的,再证明相似的,△ACE 是等腰直角三角形,所以不可能同其他三角形相似;又△ACD 是直角三角形,所以不可能和非直角三角形△ADE 、△ABD 、△ABE 相似；又△ACD 和△ACB 对应边的比不相等,所以一也不可能相似;因为∠AED=∠BEA ，所以△AED 和△BEA 可能相似.证明:设AC=CE=ED=DB=a.,2,22a EB ED a AE =⋅=.2EB ED AE ⋅= 即AEEB ED AE =.∠AED=∠BEA ， △AED ∽△BEA.反思:对于具体问题，一定要灵活处理.因为此题出现三角形较多,首先要“快刀斩乱麻”去掉那些不可能相似的三角形，再来检验那些可能相似的三角形. 例3:(苏州)如图3，梯形ABCD 中．AB ∥CD ．AB=2CD ，E,F 分别是AB ，BC 的中点.EF 与BD 相交于点M ．(1)求证：△EDM ∽△FBM ；(2)若DB=9，求BM ．分析：(1)从已知条件中易推出BE=CD,BE ∥CD,于是根据一组对边平行且相等的四边形为平行四边形，得四边形DCBE 是平行四边形.因此CB ∥DE,故可推出△EDM ∽△FBM. (2)利用(1)中的△EDM ∽△FBM ，可得,BFDE BM DM =而F 为BC 的中点，得DE=2BF,DM=2EB.故BM 为所求. 解：(1)∵E 是AB 的中点,∴AB=2EB.∵AB ∥CD,∴四边形CBED 为平行四边形,∴ CB ∥DE.∴∠DEM=∠BFM, ∠EDM=∠FBM. ∴△EDM ∽△FBM.(2) ∵△EDM ∽△FBM, ∴BFDE BM DM =.∵F 是BC 的中点,∴ DE=2BF. ∴DM=2BM,∴BM=.331=DB图2BA 图3反思:遇到有平行条件时,通常利用平行线的性质;借助平行线的性质,找相等的角来证明三角形相似.例4:如图4,已知在△ABC 中, ∠C=,900D 、E 分别为AB 、BC 上的点,且.BC BE AB BD ⋅=⋅求证:DE ⊥AB.分析:证垂直的方法很多,我们已知当一个三角形与已知直角三角形全等,那么这个三角形也是直角三角形,类似地,我们也可以通过证一个三角形与已知三角形相似来证明垂直问题，而由∠B 为公共角, .BC BE AB BD ⋅=⋅可得△ABC ∽△EBD,故问题得证.证明: ∵.BC BE AB BD ⋅=⋅∠B=∠B, ∴△ABC ∽△EBD.∴∠EDB=∠C.又∵∠C=,900∴∠EDB=.900 ∴DE ⊥AB.反思:若将题设里的BC BE AB BD ⋅=⋅与结论DE ⊥AB 交换后,该如何证明?请与同伴交流你的证明思路.图4。

7相似三角形的性质第1课时相似三角形的性质(一)1.[2015·浦东新区月考]如果两个相似三角形对应边中线之比是1∶4,那么它们的对应高之比是()A.1∶2B.1∶4C.1∶8D.1∶162.如图4-7-4,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC 的值为()图4-7-4A.9:4B.9:2C.3:4D.3:23.如图4-7-5,某校宣传栏后面2 m处种了一排树,每隔2 m一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3 m处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为m.(不计宣传栏的厚度)图4-7-54.如图4-7-6是一个照相机成像的示意图.图4-7-6(1)如果像高MN是35 mm,像距LC是50 mm,拍摄的景物高度AB是4.9 m,拍摄点离景物有多远?(2)如果要完整地拍摄高度是2 m的景物,拍摄点离景物有4 m,像高不变,则相机的像距应调整为多少?5.如图4-7-7,在△ABC中,∠ACB=90°,CD⊥AB于D,AE是∠CAB的平分线,且交CD于点E,交CB于点F.求证:AF:AE= CB:C D.图4-7-7答案解析1.B2.D【解析】∵∠ACB=90°,CD⊥AB,∠A为公共角,∴△ACB∽△ADC,同理由∠B为公共角可得△ACB∽△CDB,∴△ACB∽△ADC∽△CDB,即==,∵AD:BD=9:4,可令AD=9x,BD=4x,则=,即CD=6x,∴AC:BC=AD∶CD=9x:6x=3:2.故选D.3.【解析】根据题意,小树每隔2 m一棵,共种了6棵.∴BC=2×5=10(m),CG===5(m).由图形可知△AEF∽ACG,∴=,即=,解得EF=3 m.∴DE=2EF=2×3=6(m).4.【解析】利用相似三角形对应边上的高等于相似比即可列出比例式求解.弄清题中小孔成像原理的图形信息是解决本题的前提条件.灵活运用相似三角形对应高的比等于相似比列方程求解是解决此类题的常用方法.解:根据物体成像原理知:△LMN∽△LBA,∴=,即=.(1)∵像高MN=35 mm,像距LC=50 mm,拍摄的景物高度AB=4.9 m,∴=,解得LD=7,∴拍摄点距离景物7 m;(2)拍摄高度是2 m的景物,拍摄点离景物有4 m,像高不变,∴=,解得LC=70,∴相机的像距应调整为70 mm.5.证明:∵CD⊥AB,∴∠CDA=90°,又∵∠ACB=90°,∠CAB =∠CAD,∴△ABC∽△ACD,又∵AF,AE分别是△ABC和△ACD的内角平分线,∴AF:AE= CB:C D.。