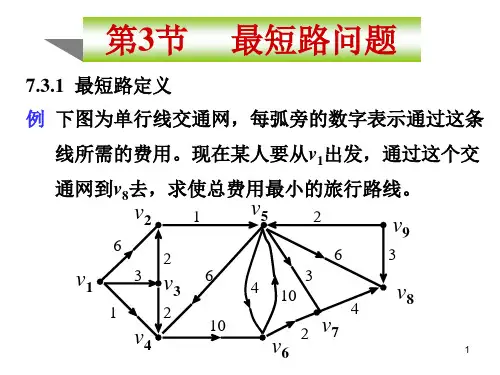
第三章最短路问题
- 格式:pptx
- 大小:383.87 KB
- 文档页数:52
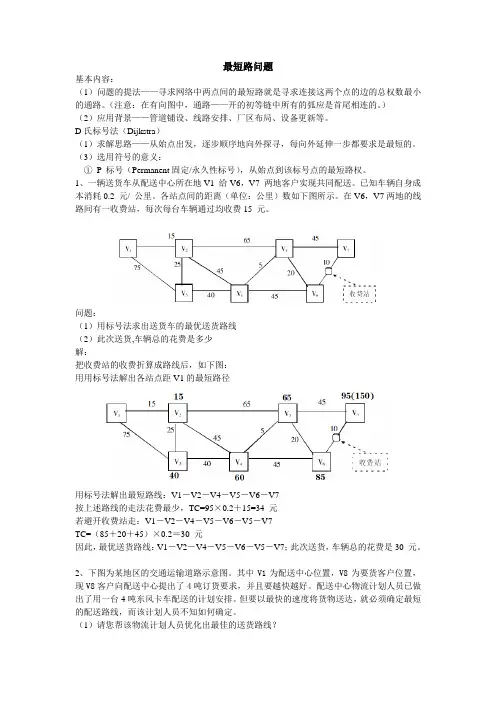
最短路问题基本内容:(1)问题的提法——寻求网络中两点间的最短路就是寻求连接这两个点的边的总权数最小的通路。
(注意:在有向图中,通路——开的初等链中所有的弧应是首尾相连的。
)(2)应用背景——管道铺设、线路安排、厂区布局、设备更新等。
D氏标号法(Dijkstra)(1)求解思路——从始点出发,逐步顺序地向外探寻,每向外延伸一步都要求是最短的。
(3)选用符号的意义:①P 标号(Permanent固定/永久性标号),从始点到该标号点的最短路权。
1、一辆送货车从配送中心所在地V1 给V6,V7 两地客户实现共同配送。
已知车辆自身成本消耗0.2 元/ 公里。
各站点间的距离(单位:公里)数如下图所示。
在V6,V7两地的线路间有一收费站,每次每台车辆通过均收费15 元。
问题:(1)用标号法求出送货车的最优送货路线(2)此次送货,车辆总的花费是多少解:把收费站的收费折算成路线后,如下图:用用标号法解出各站点距V1的最短路径用标号法解出最短路线:V1-V2-V4-V5-V6-V7按上述路线的走法花费最少,TC=95×0.2+15=34 元若避开收费站走:V1-V2-V4-V5-V6-V5-V7TC=(85+20+45)×0.2=30 元因此,最优送货路线:V1-V2-V4-V5-V6-V5-V7;此次送货,车辆总的花费是30 元。
2、下图为某地区的交通运输道路示意图。
其中V1为配送中心位置,V8为要货客户位置,现V8客户向配送中心提出了4吨订货要求,并且要越快越好。
配送中心物流计划人员已做出了用一台4吨东风卡车配送的计划安排。
但要以最快的速度将货物送达,就必须确定最短的配送路线,而该计划人员不知如何确定。
(1)请您帮该物流计划人员优化出最佳的送货路线?(2)已知车辆的平均行驶速度为50公里/小时,如早晨8:00发车,货物什么时间可以送达客户?解:用T 标号法求解得最短路线为:V1-V2-V3-V6-V7-V8。
![[管理学]最短路问题](https://uimg.taocdn.com/53ce6a346c175f0e7cd1376c.webp)


最短路问题(short-path problem)若网络中的每条边都有一个权值值(长度、成本、时间等),则找出两节点(通常是源节点与结束点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
最短路问题,我们通常归属为三类:单源最短路径问题(确定起点或确定终点的最短路径问题)、确定起点终点的最短路径问题(两节点之间的最短路径)1、Dijkstra算法:用邻接矩阵a表示带权有向图,d为从v0出发到图上其余各顶点可能达到的最短路径长度值,以v0为起点做一次dijkstra,便可以求出从结点v0到其他结点的最短路径长度代码:procedure dijkstra(v0:longint);//v0为起点做一次dijkstrabegin//a数组是邻接矩阵,a[i,j]表示i到j的距离,无边就为maxlongintfor i:=1 to n do d[i]:=a[v0,i];//初始化d数组(用于记录从v0到结点i的最短路径), fillchar(visit,sizeof(visit),false);//每个结点都未被连接到路径里visit[v0]:=true;//已经连接v0结点for i:=1 to n-1 do//剩下n-1个节点未加入路径里;beginmin:=maxlongint;//初始化minfor j:=1 to n do//找从v0开始到目前为止,哪个结点作为下一个连接起点(*可优化) if (not visit[j]) and (min>d[j]) then//结点k要未被连接进去且最小begin min:=d[j];k:=j;end;visit[k]:=true;//连接进去for j:=1 to n do//刷新数组d,通过k来更新到达未连接进去的节点最小值,if (not visit[j]) and (d[j]>d[k]+a[k,j]) then d[j]:=a[k,j]+d[k];end;writeln(d[n]);//结点v0到结点n的最短路。

最短路问题数学模型
最短路问题是指在带权有向图中,求两个顶点之间的最短路径。
这个问题在现实生活中有很多应用,如在交通规划、电信网络设计、人工智能等领域。
为了解决这个问题,需要建立一个数学模型。
数学模型是指用数学方法对实际问题进行抽象和描述,从而进行定量分析和求解的方法。
对于最短路问题,可以使用图论和运筹学的方法建立数学模型。
在图论中,最短路问题可以使用迪杰斯特拉算法或弗洛伊德算法求解。
这些算法基于图的边权和,采用动态规划的思想,逐步计算每个节点到源节点的最短距离,最终得到整个图中每对节点之间的最短路径。
在运筹学中,最短路问题可以被看作是一种线性规划问题。
可以将每个节点看作是一个决策变量,节点之间的边权看作是线性约束条件,目标函数则是从源节点到目标节点的路径长度。
通过对目标函数进行最小化,可以得到最短路径的解。
总之,最短路问题数学模型可以通过图论和运筹学的方法进行建立和求解。
建立好的数学模型可以为实际问题提供科学解决方案,优化效率和效果。
- 1 -。

最短路问题何谓最短路?最短路问题考虑的是有向网络N=(V,A,W),其中弧(i,j)∈A 对应的权又称为弧长或费用。
对于其中的两个顶点s,t∈V,以s 为起点,t 为终点的有向路称为s-t 有向路,其所经过的所有弧上的权(或弧长、费用)之和称为该有向路的权(或弧长、费用)。
所有s-t 有向路中权最小的一条称为s-t 最短路。
ij w 如何得到最短路?最短路问题的线性规划描述如下:(,)m i ni j i j i j A w x ∈∑ (1):(,):(,)1,,..1,,0,,ij ji j i j A j j i A i s s t x x s i s t ∈∈=⎧⎪t −=−=⎨⎪≠⎩∑∑ (2) 0ij x ≥ (3) 其中决策变量表示弧(i,j)是否位于s-t 路上:当=1时,表示弧(i,j)位于s-t 路上,当=0时,表示弧(i,j)不在s-t 路上。
本来,应当是0-1变量,但由于约束(2)的约束矩阵就是网络的关联矩阵,它是全幺模矩阵,因此0-1变量可以松弛为区间[0,1]中的实数(当用单纯形法求解时,将得到0-1整数解)。
ij x ij x ij x ij x 值得注意的是,我们这里将变量直接松弛为所有非负实数。
实际上,如果可以取0-1以外的整数,则约束条件并不能保证对应于非零的弧所构成的结构(记为P)一定是一条路,因为这一结构可能含有圈。
进一步分析,我们总是假设网络本身不含有负圈,而任何正圈不可能使目标函数最小,因此上面的约束条件(2),(3)可以保证当达到最优解时,P 如果包含圈,该圈一定是零圈,我们从P 中去掉所有的零圈,就可以得到最短路。
ij x ij x ij x 无圈网络与正费用网络一般采用标号设定算法。
Bellman 方程(最短路方程)将约束条件(2)两边同时乘以-1,得到其对偶问题为:m ax()t s u u − (4)..,(,)j i ij s t u u w i j A −≤∀∈ (5)根据互补松弛条件,当x 和u 分别为原问题和对偶问题的最优解时:()0,(,i j j i i j )x u u w i j −−=∀∈A (6) 因此,当某弧(i,j)位于最短路上时,即对应的变量>0时,一定有ij x j i i u u w −=j 。



郑州大学硕士学位论文网络最短路的解集结构及有关问题姓名:张振坤申请学位级别:硕士专业:运筹学与控制论指导教师:罗来兴;林诒勋2002.5.1中文摘要网络最短路问题是一个基本的离散最优化问题,一般的有限状态多阶段决策过程都可以转化为它。
因此,最短路问题有着很广泛的应用意义。
f其定义如下㈨:给定一个有向或无向图(网络)N=(V,A)和每一个弧ej∈A上的非负权。
;>/o,其中y为点集,A为弧集。
最短路问题就是求从一个始点s到另一个终点t的一条路,使得路上弧的总权和最/j,J本文所研究的问题是对网络最短路问题的进一步讨论,由以下3个部分组成:1.网络最短路的最优镌.0瞄;2.网络最短路的曩垡童掺结构;3.多端最短路的缝蕉攥型。
(1.网络最短路的最优解邻域\文[6,9]介绍了第k条最短路的概念和算法。
在此基础上,第二章讨论了最短路的最优解邻域的求解问题,得到了求解一个网络N的等势网络N。
的算法思想、求解网络N的所有最短路的算法2.1以及求解所有处于最优解邻域中的非最短路的算法2.2。
定理1网络N的等势网络N。
包含N中所有的(s。
t)最短路,并且N。
可以在多项式时间内找到,算法复杂性为O(m),其中m=IAI。
定理2在网络N的任意一条长度小于或等于£‘+e的(5,t)路中,任意中间顶点{的位势嘶必小于或等于z。
+e。
定理3在网络Ⅳ中,对任意一条通过顶点i∈V\“的路P,若路P的路长z≤£。
+e,则必有”f+?ti7≤Z’+£2网络最短路的最优解集结构本文在第三章中研究了网络最短路的最优解集结构:首先讨论了一个网络N具有唯一一条最短路的充要条件;其次,借助于2一变换的定义,着重探讨了网络最短路的2一变换图的结构性质。
定理4对等势予网络N。
中一个(s,t)有向路P,它是N中唯一一条最短路的充分必要条件是:在N。
中不存在起点和终点都在P上的等长2一重路。
定理5网络N的最短路2一变换图为平凡图,当且仅当网络N只有一条最短路。
