小学数学数论问题

小升初专项训练---数论数论在数学中的地位是独特的，高斯曾经说过“数学是科学的皇后，数论是数学中的皇冠”。

翻开任何一本数学辅导书，数论的内容都占据了不少的版面。

在小升初择校考试及小学各类数学竞赛中，直接运用数论知识解题的题目分值大概占据整张试卷总分的12%左右，小学阶段的数论知识点主要有：1、质数与合数、因数与倍数、分解质因数2、数的整除特征及整除性质3、余数的性质、同余问题4、位值原理5、最值问题知识点一：质数与合数、因数与倍数、分解质因数1.质数与合数突破要点——质数合数分清楚，2是唯一偶质数(1)质数：一个数除了1和它本身以外，没有其他的因数，这样的数统称质数。

(2)合数：一个数除了1和它本身以外，还有其他的因数，这样的数统称合数。

例如：4、6、8、10、12、14，…都是合数。

在100以内有2、3、5、7、11、13、17、19、23、29、31、37、41、47、53、59、61、67、71、73、79、83、89、97共25个质数2约数与倍数公因数短除法到一个不能除为止，公倍数除到海枯石烂为止，因数有限个，倍数无穷多。

如果一个自然数a能被自然数b整除，那么称a为b的倍数，b为a的约数。

如果一个自然数同时是若干个自然数的约数，那么称这个自然数是这若干个自然数的公约数。

在所有公约数中最大的一个公约数，称为这若干个自然数的最大公约数。

自然数a1，a2，…，an的最大公约数通常用符号（a1，a2，…，an）表示，例如，（6，9，15）=3。

3．质因数与分解质因数（1）如果一个质数是某个数的约数，那么就是说这个质数是这个数的质因数。

（2）把一个合数用质因数相乘的形式表示出来，叫做分解质因数。

例如，把42分解质因数，即是42=2×3×7。

其中2、3、7叫做42的质因数。

又如，50=2×5×5，2、5都叫做50的质因数。

4、要注意以下几条：（1）1既不是质数，也不是合数。

优秀篇奇偶性1.（1984 年第1 届迎春杯试题）有6 个学生都面向南站成一行，每回只能有5 个学生向后转，则最少要转回就能使这6 个学生都面向北．2.是否可在下列各数之间添加加号或者减号，使得等式成立？1 2 3 4 5 6 7 8 9 10 45若可以，请写出符合条件的等式；若不可以，请说明理由。

位值原理3.(2009 年第7 届希望杯5 年级2 试第4 题，5 分)一个十位数字是0 的三位数，等于它的各位数字之和的67 倍，交换这个三位数的个位数字和百位数字，得到的新三位数是它的各位数字之和的倍。

4. a ，b ，c 分别是三位数中的不同的数码，用a ，b ，c 共可组成六个三位数，如果其中五个三位数之和是2234 ，那么另一个三位数是几？数的整除5.（2008 年西城实验数学水平测试）一个自然数的末两位数字为17，它的数字和为17，且能被17整除．请你写出满足条件的最小五位自然数：6. 300301302303304…998999 能否被11 整除？如果不能，那么余数是多少？7. 已知一个五位回文数等于45 与一个四位回文数的乘积（即abcba = 45⨯deed ），那么这个五位回文数最大的可能值是.8. （2008 年第6 届走美杯4 年级决赛第6 题，10 分）207 ，2007 ，20007 ，等首位是2 ，个位是7 ，中间数字全部是0 的数字中，能被27 整除而不被81整除的最小数是。

9. 六位数20□□08 能被99 整除，□□是.10.在小于5000 的自然数中，能被11 整除，并且数字和为13 的数，共有个．质数、合数11.（2010 年十一学校试题）与6 互质的最小的合数是多少？12.（2010 年“数学解题能力展示”六年级初试第5 题）用0～9 这10 个数字组成若干个合数，每个数字都恰好用一次，那么这些合数之和的最小值是．13.（2009 年西城实验小升初试题）若三个不同的质数ab2c +a = 2006 .求a +b +c 的值.因数与倍数14.（2010 年第8 届希望杯6 年级2 试试题）张老师带领六（1）班的学生会种树，学生恰好可平均分成5 组，已知师生每人种的树一样多，共种树527 棵，则六（1）的学生有人。

数论50题1．由1，3，4，5，7，8这六个数字所组成的六位数中，能被11整除的最大的数是多少？【分析】各位数字和为1+3+4+5+7+8=28所以偶数位和奇数位上数字和均为14为了使得该数最大，首位必须是8，第2位是7，14-8=6那么第3位一定是5，第5位为1该数最大为875413。

2．请用1，2，5，7，8，9这六个数字（每个数字至多用一次）来组成一个五位数，使得它能被75整除，并求出这样的五位数有几个？【分析】75=3×25若被3整除，则各位数字和是3的倍数，1+2+5+7+8+9=32所以应该去掉一个被3除余2的，因此要么去掉2要么去掉8先任给一个去掉8的，17925即满足要求1）若去掉8则末2位要么是25要么是75，前3位则任意排，有3！=6种排法因此若去掉8则有2*6=12个满足要求的数2）若去掉2则末2位只能是75，前3位任意排，有6种排法所以有6个满足要求综上所述，满足要求的五位数有18个。

3．已知道六位数20□279是13的倍数，求□中的数字是几？【分析】根据被13整除的判别方法，用末三位减去前面的部分得到一个两位数，十位是7，个位是（9-□），它应该是13的倍数，因为13|78,所以9-□=8□中的数字是14．某自然数，它可以表示成9个连续自然数的和，又可以表示成10个连续自然数的和，还可以表示成11个连续自然数的和，那么符合以上条件的最小自然数是？（2005全国小学数学奥赛）【分析】可以表示成连续9个自然数的和说明该数能被9整除，可以表示成连续10个自然数的和说明该数能被5整除，可表示成连续11个自然数的和说明该数能被11整除因此该数是[9,5,11]=495，因此符合条件的最小自然数是495。

5．一次考试中，某班同学有考了优秀，考了良好，考了及格，剩下的人不及格，已知该班同学的人数不超过50，求有多少人不及格？【分析】乍一看这应该是一个分数应用题，但实际上用到的却是数论的知识，由于人数必须是整数，所以该班同学的人数必须同时是2，3，7的倍数，也就是42的倍数，又因为人数不超过50，所以只能是42人，因此不及格的人数为（1---）×42=1人6．（1）从1到3998这3998个自然数中，有多少个能被4整除？（2）从1到3998这3998个自然数中，有多少个数的各位数字之和能被4整除？（第14届迎春杯考题）【分析】（1）3998/4=999….6所以1-3998中有996个能被4整除的（2）考虑数字和，如果一个一个找规律我们会发现规律是不存在的因此我们考虑分组的方法我们补充2个数，0000和3999，此外所有的一位两位三位数都在前面加上0补足4位然后对这4000个数做如下分组（0000，1000，2000，3000）（0001，1001，2001，3001）（0002，1002，2002，3002）…….(0999，1999，2999，3999)共1000组，容易发现每一组恰好有个数字和是4的倍数，因此共有1000个数字和是4的倍数但注意到我们补充了一个0000进去。

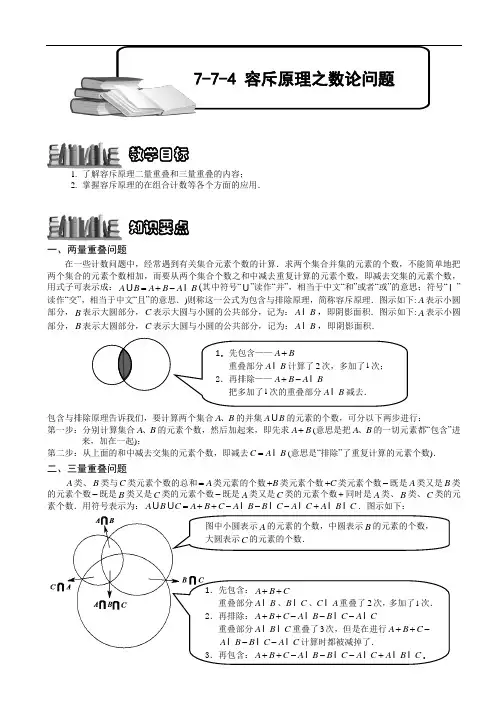
1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-U I (其中符号“U ”读作“并”，相当于中文“和”或者“或”的意思；符号“I ”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B U 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =I (意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+U U I I I I I ．图示如下：教学目标知识要点1．先包含——A B +重叠部分A B I 计算了2次，多加了1次； 2．再排除——A B A B +-I把多加了1次的重叠部分A B I 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++重叠部分A B I 、B C I 、C A I 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++---I I I重叠部分A B C I I 重叠了3次，但是在进行A B C ++- A B B C A C --I I I 计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+I I I I I ．7-7-4 容斥原理之数论问题在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．例题精讲【例 1】在1~100的全部自然数中，不是3的倍数也不是5的倍数的数有多少个？【巩固】在自然数1100~中，能被3或5中任一个整除的数有多少个？【巩固】在前100个自然数中，能被2或3整除的数有多少个？【例 2】在从1至1000的自然数中，既不能被5除尽，又不能被7除尽的数有多少个?【巩固】求在1至100的自然数中能被3或7整除的数的个数．【例 3】以105为分母的最简真分数共有多少个？它们的和为多少？【巩固】分母是385的最简真分数有多少个？并求这些真分数的和.【例 4】在1至2008这2008个自然数中，恰好是3、5、7中两个数的倍数的数共有个．【例 5】求1到100内有____个数不能被2、3、7中的任何一个整除。

千里之行，始于足下。

第 1 页/共 3 页
【例】一个数除以4余2，除以5余3，则这个数最小是？
【例】一个数除以3余2，除以4余1，则这个数最小是？
(★★★)
两位天然数ab 与ba 除以7都余1，并且a ＞b ，求ab ba ⨯
小升初数论重点考查内容
朽木易折，金石可镂。

(★★★) (2005年全国小学数学奥林匹克试题)
有一个整数，用它去除70，110，160所得到的3个余数之和是50，那么这个整数是________。

(★★★) (2008年第十二届香港保良局小学数学世界邀请赛个人赛)
试求22008＋20082除以7的余数。

(★★★)(2009年第十届中环杯五年级试题)
有一个数除以3余数是2，除以5余数是3，那么这个数除以15的余数是( )
(★★★★)(1998年小学数学奥林匹克预赛B卷)
一个小于200的数，它除以11余8，除以13余10，那么这个数是______。

(★★★★)( 1998年小学数学奥林匹克预赛)
某数除以11余8，除以13余10，除以17余12，那么这个数的最小可能值是______。

千里之行，始于足下。

第 3 页/共 3 页。

小学数论试题及答案一、选择题（每题3分，共30分）1. 一个数是3的倍数，那么这个数的各位数字之和一定是3的倍数。

这个说法是：A. 正确B. 错误2. 以下哪个数是质数？A. 4B. 9C. 11D. 153. 两个连续的自然数相加，和一定是：A. 质数B. 合数C. 偶数D. 奇数4. 一个数的因数的个数是有限的，那么这个数是：A. 质数B. 合数C. 偶数D. 奇数5. 一个数的倍数的个数是无限的，那么这个数是：A. 质数B. 合数C. 偶数D. 奇数6. 一个数的约数中最大的一个是它本身，那么这个数是：A. 质数B. 合数C. 偶数D. 奇数7. 以下哪个数是2的倍数？A. 23B. 37C. 42D. 598. 一个数是5的倍数，那么这个数的个位数字一定是：A. 0B. 2C. 5D. 89. 一个数是3的倍数，那么这个数的各位数字之和一定是：A. 3的倍数B. 2的倍数C. 5的倍数D. 7的倍数10. 以下哪个数是3的倍数？A. 123B. 234C. 345D. 456二、填空题（每题4分，共20分）1. 一个数的最小倍数是______。

2. 一个数的最大因数是______。

3. 一个数的因数的个数是______的。

4. 一个数的倍数的个数是______的。

5. 一个数的约数中最大的一个是______。

三、解答题（每题10分，共50分）1. 证明：如果一个数是偶数，那么它的倍数也是偶数。

2. 证明：如果两个数都是质数，那么它们的和一定是偶数。

3. 证明：如果一个数是3的倍数，那么这个数的各位数字之和也是3的倍数。

4. 证明：如果一个数是5的倍数，那么这个数的个位数字一定是0或5。

5. 证明：如果一个数是质数，那么它只有两个因数。

答案：一、选择题1. A2. C3. B4. B5. B6. A7. C8. C9. A10. A二、填空题1. 它本身2. 它本身3. 有限4. 无限5. 它本身三、解答题1. 证明：如果一个数是偶数，那么它可以表示为2n（n为整数）。

小学数学四年级初等数论一、幻方1、三阶幻方：a)中心数=幻和÷3b)经过中心数的4组数是等差数列c)九宫者，二四为肩，六八为足，左三右七，戴九履一，五居中央。

依次对齐，按照口诀对应填写。

2、四阶幻方：把16个数从小到大依次填入，同一对角线的数字对调即可例题1：在下面两幅图的每个空格中，填入7个自然数，使得每行、每列、每条对角线上的三个数之和等于21。

例题2：如图，有一个11位数，它的每3个相邻数字之积都是126。

标有＊的那个数位上的数字应是。

例题3：表中数的排列顺序，2007在第几行第几列？2007的下边是哪个数？例题4：在一个乘法幻方中，每一行、每一列、对角线上的数之积都相等。

如果在图中的空格中填上正整数，构成一个乘法幻方，那么x的值是多少？例题5：把10~20这11个数分别填入下图的各圆圈内，使每条线段上3个圆内所填数的和都等于45。

二、数字奇偶性知识点：1、奇数+奇数=偶数奇数+偶数=奇数偶数+偶数=偶数2、奇数×奇数=奇数偶数×偶数（奇数）=偶数3、和差偶数，奇偶相同；和差奇数，奇偶相反4、和与差奇偶相同5、奇数的平方除以8余1，偶数的平方是4的倍数A）简单的：例题1、若三个连续奇数的和是111，则其中最小的奇数是（）例题2、有一个两位数，分别在这个数的左边、中间、右边写一个1，得到三个三位数，若这三个三位数的和是1257，求原来的两位数。

例题3、用20厘米长的铜丝弯成边长是整数的长方形，这样的长方形不止一种，其中，面积最小的，长（）厘米，宽（）厘米；面积最大的，长（）厘米，宽（）厘米。

例题4、将190表示成10个连续偶数的和，其中最大的偶数是（）例题5、从1~9这9个数中任取一个奇数和一个偶数相乘，不同的乘积有（）个。

例题6、有三个连续的奇数，已知前两个数的积与后两个数的积的差是252，则这三个连续奇数中最小的数是（）例题7、已知m>1，m个连续的自然数的和是33，则m的所有可能取的值是（）例题8、如果两个整数的和与差的积是77，那么这两个数是（）和（）例题9、乘积是160的两个数的和比这两个数的差大4，则这两个数的和是（）例题10、1×2+2×3×4+3×4×5×6+4×5×6×7×8+⋯+10×11×12×13×…×20的末位数字是（）例题11、小明有一本40页的故事书，非常可惜被撕掉了一页，现在所剩的页码之和为793，小明的故事书被撕掉的这一页的页码为（）例题12、一个数除以9，商和余数是相同地不为零地自然数，这个数最小是（）例题13、一个不为零地自然数，除以3和除以5的商和余数相同，则这个数是（）例题14、求一切除以6后余2的两位数的和例题15、在1-200的自然数中，求既是3的倍数，又是4的倍数的所有自然数的和。

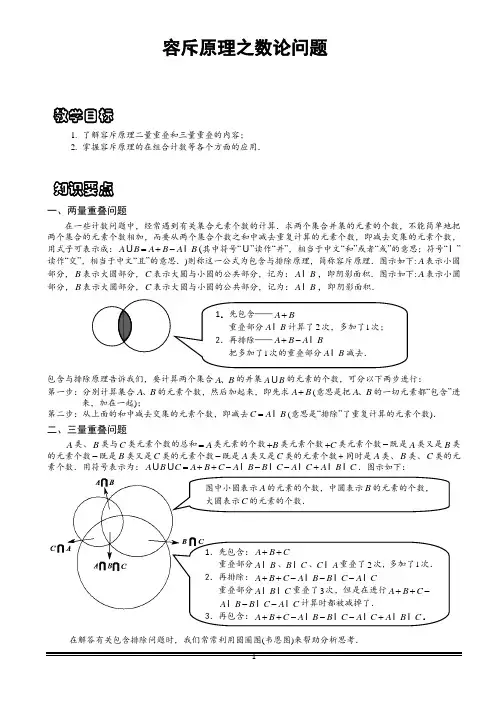
容斥原理之数论问题1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-(其中符号“”读作“并”，相当于中文“和”或者“或”的意思；符号“”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B 的元素的个数，可分以下两步进行： 第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =(意思是“排除”了重复计算的元素个数)． 二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+．图示如下：在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．教学目标知识要点 1．先包含——A B + 重叠部分A B 计算了2次，多加了1次； 2．再排除——A B A B +- 把多加了1次的重叠部分A B 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++ 重叠部分A B 、B C 、C A 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++--- 重叠部分A B C 重叠了3次，但是在进行A B C ++- A B B C A C --计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+．【例 1】 在1~100的全部自然数中，不是3的倍数也不是5的倍数的数有多少个？ A B【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 如图，用长方形表示1~100的全部自然数，A 圆表示1~100中3的倍数，B 圆表示1~100中5的倍数，长方形内两圆外的部分表示既不是3的倍数也不是5的倍数的数．由1003331÷=可知，1~100中3的倍数有33个；由100520÷=可知，1~100中5的倍数有20个；由10035610÷⨯=（）可知，1~100既是3的倍数又是5的倍数的数有6个．由包含排除法，3或5的倍数有：3320647+-=(个)．从而不是3的倍数也不是5的倍数的数有1004753-=(个)．【答案】53【巩固】 在自然数1100~中，能被3或5中任一个整除的数有多少个？【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 1003331÷=，100520÷=，10035610÷⨯=（）．根据包含排除法，能被3或5中任一个整除的数有3320647+-=(个)．【答案】47【巩固】 在前100个自然数中，能被2或3整除的数有多少个？【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 如图所示，A 圆内是前100个自然数中所有能被2整除的数，B 圆内是前100个自然数中所有能被3整除的数，C 为前100个自然数中既能被2整除也能被3整除的数．前100个自然数中能被2整除的数有：100250÷=(个)．由1003331÷=知，前100个自然数中能被3整除的数有：33个．由10023164÷⨯=（）知，前100个自然数中既能被2整除也能被3整除的数有16个．所以A 中有50个数，B 中有33个数，C 中有16个数．因为A ，B 都包含C ，根据包含排除法得到，能被2或3整除的数有：50331667+-=(个)．【答案】67【例 2】 在从1至1000的自然数中，既不能被5除尽，又不能被7除尽的数有多少个?【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 1～1000之间，5的倍数有10005⎡⎤⎢⎥⎣⎦=200个，7的倍数有10007⎡⎤⎢⎥⎣⎦=142个，因为既是5的倍数，又是7的倍数的数一定是35的倍数，所以这样的数有100035⎡⎤⎢⎥⎣⎦=28个． 所以既不能被5除尽，又不能被7除尽的数有1000-200-142+-28=686个．【答案】686【巩固】 求在1至100的自然数中能被3或7整除的数的个数．【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 记 A ：1～100中3的倍数，1003331÷=，有33个；B ：1～100中7的倍数，1007142÷=，有14个；A B ：1～100中3和7的公倍数，即21的倍数，10021416÷=，有4个．依据公式，1～100中3的倍数或7的倍数共有3314443+-=个，则能被3或7整除的数的个数为43个.【答案】43例题精讲【例3】以105为分母的最简真分数共有多少个？它们的和为多少？【考点】容斥原理之数论问题【难度】4星【题型】解答【解析】以105为分母的最简真分数的分子与105互质，105=3×5×7，所以也是求1到105不是3、5、7倍数的数有多少个，3的倍数有35个，5的倍数有21个，7的倍数有15个，15的倍数有7个，21的倍数有5个，35的倍数有3个，105的倍数有1个，所以105以内与105互质的数有105-35-21-15+7+5+3-1=48个，显然如果n与105互质，那么（105-n）与n互质，所以以105为分母的48个最简真分数可两个两个凑成1，所以它们的和为24.【答案】48个，和24【巩固】分母是385的最简真分数有多少个？并求这些真分数的和.【考点】容斥原理之数论问题【难度】4星【题型】解答【解析】385=5×7×11，不超过385的正整数中被5整除的数有77个；被7整除的数有55个；被11整除的数有35个；被77整除的数有5个；被35整除的数有11个；被55整除的数有7个；被385整除的数有1个；最简真分数的分子可以有385-77-55-35+5+11+7-1=240.对于某个分数a/385如果是最简真分数的话，那么（385-a）/385也是最简真分数，所以最简真分数可以每两个凑成整数1，所以这些真分数的和为120.【答案】240个，120个【例4】在1至2008这2008个自然数中，恰好是3、5、7中两个数的倍数的数共有个．【考点】容斥原理之数论问题【难度】3星【题型】填空【关键词】西城实验【解析】1到2008这2008个自然数中，3和5的倍数有200813315⎡⎤=⎢⎥⎣⎦个，3和7的倍数有20089521⎡⎤=⎢⎥⎣⎦个，5和7的倍数有20085735⎡⎤=⎢⎥⎣⎦个，3、5和7的倍数有200819105⎡⎤=⎢⎥⎣⎦个．所以，恰好是3、5、7中两个数的倍数的共有1331995195719228-+-+-=个．【答案】228个【例5】求1到100内有____个数不能被2、3、7中的任何一个整除。

数论初步例题和知识点总结数论是数学中一个古老而重要的分支，它主要研究整数的性质和关系。

在这篇文章中，我们将通过一些例题来深入理解数论中的关键知识点。

一、整除整除是数论中的基本概念。

如果整数 a 除以整数 b（b≠0），商是整数且没有余数，我们就说 a 能被 b 整除，记作 b ｜ a。

例如，15÷3 ＝ 5，没有余数，所以 3 ｜ 15。

例题：判断 28 能否被 4 整除。

解：因为 28÷4 ＝ 7，商是整数且没有余数，所以 4 ｜ 28。

整除有以下几个重要性质：1、如果 a ｜ b 且 b ｜ c，那么 a ｜ c。

2、如果 a ｜ b 且 a ｜ c，那么对于任意整数 m、n，有 a ｜（mb ＋ nc)。

二、质数与合数质数是指一个大于 1 的自然数，除了 1 和它自身外，不能被其他自然数整除的数。

合数则是指除了能被 1 和本身整除外，还能被其他数（0 除外）整除的自然数。

例如，2、3、5、7 是质数，而 4、6、8、9 是合数。

例题：判断 19 是质数还是合数。

解：因为 19 只能被 1 和 19 整除，所以 19 是质数。

质数有一个重要的定理——算术基本定理：任何一个大于 1 的整数都可以唯一分解成若干个质数的乘积。

三、最大公因数和最小公倍数两个或多个整数共有的因数中最大的一个称为最大公因数，记作（a, b)。

两个或多个整数公有的倍数中最小的一个称为最小公倍数，记作 a, b。

例如，12 和 18 的最大公因数是 6，最小公倍数是 36。

求最大公因数和最小公倍数的方法有质因数分解法和辗转相除法。

例题：求 24 和 36 的最大公因数和最小公倍数。

质因数分解法：24 ＝ 2×2×2×336 ＝ 2×2×3×3最大公因数＝ 2×2×3 ＝ 12最小公倍数＝ 2×2×2×3×3 ＝ 72辗转相除法：用较大数除以较小数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是 0 为止。

小学奥数中的数论问题在奥数竞赛中有一类题目叫做数论题，这一部分的题目具有抽象，思维难度大，综合运用知识点多的特点，基本上出现数论题目的时候大部分同学做得都不好。

一、小学数论究包括的主要内容我们小学所学习到的数论内容主要包含以下几类：整除问题：（1）整除的性质；（2）数的整除特征（小升初常考内容）余数问题：（1）带余除式的运用被除数=除数×商+余数.（余数总比除数小）（2）同余的性质和运用奇偶问题：（1）奇偶与加减运算；（2）奇偶与乘除运算质数合数：重点是质因数的分解（也称唯一分解定理）约数倍数：（1）最大公约最小公倍数两大定理一、两个自然数分别除以它们的最大公约数，所得的商互质。

二、两个数的最大公约和最小公倍的乘积等于这两个数的乘积。

（2）约数个数决定法则（小升初常考内容）整数及分数的分解与分拆：这一部分在难度较高竞赛中常出现，属于较难的题型。

二、数论部分在考试题型中的地位在整个数学领域，数论被当之无愧的誉为“数学皇后”。

翻开任何一本数学辅导书，数论的题型都占据了显著的位置。

在小学各类数学竞赛和小升初考试中，系统研究发现，直接运用数论知识解题的题目分值大概占据整张试卷总分的30%左右，而在竞赛的决赛试题和小升初一类中学的分班测试题中，这一分值比例还将更高。

出题老师喜欢将数论题作为区分尖子生和普通学生的依据，这一部分学习的好坏将直接决定你是否可以在选拔考试中拿到满意的分数。

三、孩子在学习数论部分常常会遇到的问题数学课本上的数论简单，竞赛和小升初考试的数论不简单。

有些孩子错误地认为数论的题目很简单，因为他们习惯了数学课本上的简单数论题，比如：例1：求36有多少个约数？这道题就经常在孩子们平时的作业里和单元测试里出现。

可是小升初考题里则是：例2：求3600有多少个约数？很多孩子就懵了，因为“平时考试里没有出过这么大的数！”（孩子语）于是乎也硬着头皮用课堂上求约数的方法去求，白白浪费了大把的时间，即使最后求出结果也并不划算。