重积分部分练习题
- 格式:docx
- 大小:179.46 KB
- 文档页数:19




重积分习题三1、试求函数f(x,y)=xy2在区域D:0≤x≤1,0≤y≤1上的平均值。
2、计算二次积分3、计算二次积分4、计算二次积分5、计算二次积分6、计算二次积分7、计算二次积分8、计算二次积分9、计算二次积分10、计算二次积分11、计算二次积分12、计算二重积分其中D:|x|≤2,|y|≤1.13、计算二重积分其中D:0≤x≤1,0≤y≤2.14、计算二重积分其中D:0≤x≤a0≤y≤b.15、计算二重积分其中D:0≤x≤1,0≤y≤2.16、计算二重积分其中D:0≤x≤1,0≤y≤1.17、计算二重积分其中D:0≤x≤1,0≤y≤1.18、计算二重积分其中D:-1≤x≤1,0≤y≤2.19、计算二重积分其中D:0≤x≤2,-1≤y≤1.20、计算二重积分其中D:0≤x≤π,0≤y≤.21、计算二重积分其中D:-1≤x≤3,0≤y≤2.22、计算二重积分其中D:0≤x≤1,0≤y≤4.23、计算二重积分其中24、计算二重积分其中D:|x|≤π,|y|≤1.25、计算二重积分其中D:|x|≤3,|y|≤1.26、计算二重积分其中D:|x|≤1,0≤y≤1.27、计算二重积分其中D是以O(0,0)A(1,1)和B(0,1)为顶点的三角形区域。
28、计算二重积分其中D:0≤x≤1,-1≤y≤0.29、计算二重积分其中D:0≤y≤sin x,0≤x≤π.30、计算二重积分其中D是由曲线y=x2,直线y=0,x=2所围成区域。
31、计算二重积分其中D为由y=x,y=2x,x=4所围成的区域。
32、计算二重积分其中D:x≤y≤x,1≤x≤2.33、计算二重积分其中D是由直线x=0,y=π和y=x围成的区域。
34、计算二重积分其中D是由直线y=x,y=x+1,y=1及y=3所围成的区域。
35、计算二重积分其中36、计算二重积分其中D:-1≤x≤1,1≤y≤1.37、计算二重积分其中D:|x|≤π,0≤y≤1.38、计算二重积分其中D为由y=x,x=0,y=1所围成的区域。

第九章 重积分(A)1.填空题(1) 设()y x y x P 2,=,()23,y x y x Q =,定义于:D 10<<x ,10<<y ,则()σd y x P D⎰⎰, ()⎰⎰Dd y x Q σ,(2) 设曲顶柱体的顶面是()y x f z ,=,()D y x ∈,,侧面是母线平行于z 轴,准线为D的边界线的柱面,则此曲顶柱体的体积用重积分可表示为=V 。
(3) 在极坐标系中,面积元素为 。
2.利用二重积分的性质,比较下列积分大小(1) ()⎰⎰+Dd y x σ2与()⎰⎰+Dd y x σ3,其中积分区域D 由x 轴,y 轴以及直线1=+y x 所 围成。
(2) ()⎰⎰+D d y x σ2与()⎰⎰+Dd y x σ3,其中积分区域D 是由圆周()()21222=-+-y x 所围成。
3.利用二重积分性质,估计积分()⎰⎰++=Dd y x I σ92222的值,其中D 是圆形闭区域422≤+y x 。
4.交换积分()⎰⎰--a ax ax xa dy y x f dx 2222,的积分次序。
5.交换积分()⎰⎰-2120,ydx y x f dy 的积分次序。
6.交换二次积分()⎰⎰+-aa y y a y x f dy 022,的积分次序。
7.计算()⎰⎰+Dd y x σ23,其中D 是由两坐标轴及直线2=+y x 所围成的闭区域。
8.计算()⎰⎰+Dd y x x σcos ,其中D 是顶点分别为()0,0,()0,π和()ππ,的三角形区域。
9.计算()⎰⎰+Dyd x σsin 1,其中D 是顶点分别为()0,0,()0,1,()2,1和()1,0的梯形闭区域。
10.计算二重积分⎰⎰Ddxdy ,其中区域D 由曲线21x y -=与12-=x y 围成。
11.计算二重积分⎰⎰Dd xy σ2,其中D 是由圆周422=+y x 及y 轴所围成的右半闭区域。

重积分练习一. 填空1.⎰⎰12),(xx dy y x f dx 交换积分次序后为_________________.2.用柱面坐标系化三重积分为三次积分________________),,(=⎰⎰⎰Ωdv z y x f其中2,1,1:22===+Ωz z y x 围成. 3. (化为柱面坐标中的三次积分)__________________),,(22222211111111==⎰⎰⎰--+-------dz z y x f dydxI y x y x x x (化为柱面坐标中的三次积分) 二.选择题1. =+⎰⎰-dy y x dxx x243221( ).A. ⎰⎰302πθrdr d . B.⎰⎰232ππθrdr d C.⎰⎰3022πθdr r d . D.⎰⎰2322ππθdr r d2.若区域D 由1)1(22=+-y x 所围,则⎰⎰Ddxdy y x f ),(化成累次积分为 ( )A.⎰⎰πθθθθ0cos 20)sin ,cos (rdr r r f d . B. ⎰⎰-ππθθθθcos 20)sin ,cos (rdr r r f dC.⎰⎰20cos 20)sin ,cos (2πθθθθrdr r r f d D. ⎰⎰-22cos 20)sin ,cos (ππθθθθrdr r r f d三.计算1.. 计算⎰⎰-+=+-⋅+22)(4122222x a a xady y x a y x dx2. 计算⎰⎰-Ddxdy y x ||,其中D 是由2,0,1,0====y y x x 所围成的区域.3. 求由x e z y 222-=+与平面1,0==x x 所围立体体积.4.D 由直线x y y x ===,2,4所围成,求⎰⎰--Dxdxdy x e 22.5.计算⎰⎰-=Dd y x I σ||,其中0,0,1:22≥≥≤+y x y x D .6.计算⎰⎰⎰Ω+dV z x )(,其中22221,:y x z y x z --=+=Ω所围的空间区域.四.应用题。

重积分总复习题一 判 断1.若(,)f x y 在D 上的二重积分存在,则必定有(,)(,)DDf x y d f x y d σσ≤⎰⎰⎰⎰( )2.111(,)(,)yxdy f x y dx dx f x y dy =⎰⎰⎰⎰. ( )二 填空题1.改换二次积分的积分次序⎰⎰yy dx y x f dy 2202),(= .2.化2220)adx x y dy +⎰为极坐标形式下的二次积分为 .3.将极坐标系下的二重积分化为直角坐标系下的二重积分21(cos ,sin )d f r r rdr πθθθ⋅=⎰⎰ ___________________4.二次积分2xdx f dy ⎰的极坐标形式的二次积分为 .5.交换二次积分201111(,)(,)xxdx f x y dy dx f x y dy --+⎰⎰⎰⎰的积分次序为 .三 选择题1.设区域D :221x y +≤,f 是域D 上的连续函数,则22()Df xy dxdy +=⎰⎰( )A.12()rf r dr π⎰B .104()rf r dr π⎰ C.122()rf r dr π⎰ D.04()rrf r dr π⎰2.设4(,)xI dx f x y dy =⎰⎰,交换积分次序,得( )A.24104(,)y y dy f x y dx ⎰⎰ B.21440(,)y ydy f x y dx -⎰⎰C.44104(,)dy f x y dx ⎰⎰ D.20144(,)y y dy f x y dx ⎰⎰3.设积分区域D 由x 轴,y 轴及直线1x y +=围成,则二重积分(,)Df x y d σ⎰⎰化为累次积分后为( ).A.10dx ⎰1(,)0x f x y dy -⎰. B.10x dy -⎰1(,)0f x y dx ⎰. C.10dx ⎰1(,)0f x y dy ⎰.D.10dy ⎰1(,)0f x y dx ⎰.4.),(z y x f =在有界闭区域D 上连续是二重积分σd ),(D⎰⎰y x f 存在的( )条件。

第九章 重积分(A)1.填空题(1) 设()y x y x P 2,=,()23,y x y x Q =,定义于:D 10<<x ,10<<y ,则()σd y x P D⎰⎰, ()⎰⎰Dd y x Q σ,(2) 设曲顶柱体的顶面是()y x f z ,=,()D y x ∈,,侧面是母线平行于z 轴,准线为D的边界线的柱面,则此曲顶柱体的体积用重积分可表示为=V 。
(3) 在极坐标系中,面积元素为 。
2.利用二重积分的性质,比较下列积分大小(1) ()⎰⎰+Dd y x σ2与()⎰⎰+Dd y x σ3,其中积分区域D 由x 轴,y 轴以及直线1=+y x 所 围成。
(2) ()⎰⎰+D d y x σ2与()⎰⎰+Dd y x σ3,其中积分区域D 是由圆周()()21222=-+-y x 所围成。
3.利用二重积分性质,估计积分()⎰⎰++=Dd y x I σ92222的值,其中D 是圆形闭区域422≤+y x 。
4.交换积分()⎰⎰--a ax ax xa dy y x f dx 2222,的积分次序。
5.交换积分()⎰⎰-2120,ydx y x f dy 的积分次序。
6.交换二次积分()⎰⎰+-aa y y a y x f dy 022,的积分次序。
7.计算()⎰⎰+Dd y x σ23,其中D 是由两坐标轴及直线2=+y x 所围成的闭区域。
8.计算()⎰⎰+Dd y x x σcos ,其中D 是顶点分别为()0,0,()0,π和()ππ,的三角形区域。
9.计算()⎰⎰+Dyd x σsin 1,其中D 是顶点分别为()0,0,()0,1,()2,1和()1,0的梯形闭区域。
10.计算二重积分⎰⎰Ddxdy ,其中区域D 由曲线21x y -=与12-=x y 围成。
11.计算二重积分⎰⎰Dd xy σ2,其中D 是由圆周422=+y x 及y 轴所围成的右半闭区域。


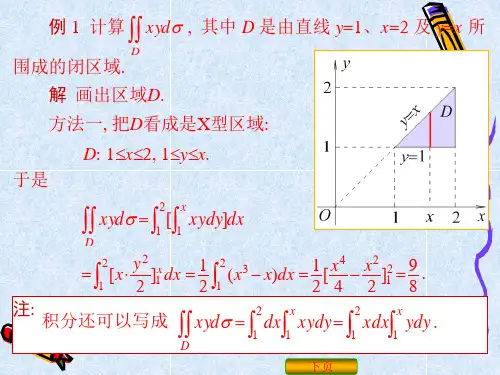
第6章 重积分练习题习题6.11.设xoy 平面上的一块平面薄片D,薄片上分布有密度为),(y x u 的电荷,且),(y x u 在D上连续,请给出薄片上电荷Q 的二重积分表达式.2.由平面1342=++z y x ,0=x , 0=y ,0=z 围成的四面体的体积为V ,试用二重积分表示V .3.由二重积分的几何意义计算⎰⎰--Dd y x Rσ222,222:R yx D ≤+.4.⎰⎰=Dd y x f I σ),(.y y x D 2:22≤+,写出I 的累次积分式.5.交换下列累次积分的积分顺序: ⑴⎰⎰--aa x a dy y x f dx 22),(. ⑵⎰⎰⎰⎰-+31301020),(),(y y dx y x f dy dx y x f dy .6.计算下列二重积分: ⑴⎰⎰+Dyx d eσ23.2||,2||:≤≤y x D . ⑵⎰⎰+Dd y x σ)(22.1||||:≤+y x D .⑶⎰⎰+Ddxdy yx221.10,10:≤≤≤≤y x D . ⑷⎰⎰--Ddxdy y x )2(21.2,:x y x y D ==.7.运用极坐标变换计算下列二重积分: ⑴⎰⎰+Ddxdy y x 22.1:22≤+yx D .⑵⎰⎰+Ddxdy y x )(22.y y x D 6:22≤+.⑶⎰⎰++Dd y x σ)1ln(22.4:22≤+y x D ,0≥x ,0≥y .8.现有一平面薄片,占有xy 平面上的区域D ,在点),(y x 处的面密度为),(y x u ,且),(y x u 在D 上连续,求该平面薄片的重心表达式.9.学习(或复习)物体转动惯量的相关物理知识.探究均匀薄片转动惯量的二重积分表达式,然后计算斜边长为a 的等腰直角梯形关于一直角边的转动惯量.习题6.21.在直角坐标系中计算下列三重积分:⑴dxdydz z xy V42⎰⎰⎰.31,20,10:≤≤≤≤≤≤z y x V .⑵dxdydz z y x V⎰⎰⎰++)sin(.V 由平面0=x ,0=y ,0=z ,2π=++z y x 围成.2.在柱面坐标系下计算三重积分dxdydzy xV⎰⎰⎰+)(22,其中V 由旋转抛物面)(2122y x z +=及平面2=z 所围成的立体.3.在球面坐标系中计算三重积分dxdydz zy x z y x V⎰⎰⎰++++222222cos ,222224:ππ≤++≤z y x V .4.运用三重积分求半径为R 的球体的体积.5.运用三重积分求球面z z y x 2222=++和锥面(以z 轴为轴,顶角为︒90)所围部分的体积.6.求曲面z z y x 8)(2222=++围成部分的体积.习题6.31.求球面16222=++z y x 被平面1=z 和2=z 所夹部分的面积.2.一段铁丝刚好围成三角形ABC ,其中)0,0(A 、)0,1(B 、)1,0(C ,三边上点),(y x 处的线密度为y x +,求这段铁丝的质量.3.求⎰τzds ,τ为圆锥螺线⎪⎩⎪⎨⎧===t z t t y t t x sin cos .4.求ds y x ⎰+τ22,其中τ为圆周x y x 222=+.5.计算⎰+Lxdy ydx ,其中L 是由点)0,1(沿上半圆122=+y x 到)0,1(-.6.)0,0(A , )1,1(B 在抛物线2x y =上,一质点从A 移动到B 沿上.在点),(y x 处所受的力F 等于该点到原点的距离,且指向原点,求力F 所作的功半圆.7.利用格林公式计算:dy y x dx y x )()(222+++⎰τ,τ为区域10≤≤x ,x y x ≤≤2的正向边界曲线.8.计算ydx x dy xy 22-⎰τ,其中τ为圆周122=+y x .9.计算球面的质量m ,已知球半径为1,球面上各点密度等于这点到铅直直径的距离.10.计算⎰⎰++SdS z y x )(.4:222=++z y x S ,0≥z .11.计算⎰⎰SzdS .S 是平面1=++z y x 在第一卦限部分.12.计算⎰⎰++Szdxdy ydxdz xdydz .S 为球面1222=++z y x 的外表面.13.用高斯公式计算上面第12题.复习题六一、判断题(正确的打“√”,错误的打“×”)1.若0),(≥y x f ,则⎰⎰Ddxdy y x f ),(的几何意义是以区域D 为底、曲面),(y x f z =为曲顶的曲顶柱体的体积. ( )2.若设}11,10|),{(≤≤-≤≤=y x y x D ,则0≥⎰⎰dxdy xe Dxy . ( )3.若设D 是由1=+y x 、1=-y x 和0=y 所围成的区域,则有=⎰⎰dxdy xy Ddy xy dx x x⎰⎰--111. ( )4.⎰⎰⎰⎰=11ln 0),(),(eeexydxy x f dy dy y x f dx . ( )5.若设L 是围成区域D 的边界曲线,则dy y x Q dx y x P L ),(),(+⎰σd yQ xP D)(∂∂-∂∂=⎰⎰. ( )二、填空题1.设}2||,1|||),{(≤≤=y x y x D ,则⎰⎰=Ddxdy .2.设}14|),{(22≤+=y xy x D ,则⎰⎰=Ddxdy .3.设}|),{(222R y x y x D ≤+=,由重积分的几何意义得⎰⎰=--Dd y x R σ222.4.若dr r r f r d dy y x f dx aa xa ⎰⎰⎰⎰--=)sin ,cos (),(22θθθβα,则=),(βα.5.设L 为椭圆14922=+yx的正向边界,=+⎰Lydy xdx cos 3 .三、选择题1.若D 是由kx y =)0(>k ,0=y 和1=x 围成的三角形区域,且⎰⎰=Ddxdy xy 1512,则=k ( )A .1B .354 C .3151 D .3522.将极坐标系下的二次积分dr r r f r d I ⎰⎰=θπθθθsin 20)sin ,cos (化为直角坐标系下的二次积分,则=I ( )A .⎰⎰--+--11111122),(y y dx y x f dy B .⎰⎰---202222),(xx xx dyy x f dx C .⎰⎰----112222),(yy yy dxy x f dy D .⎰⎰--+--11111122),(xxdyy x f dx3.二次积分⎰⎰2142),(x dy y x f dx 交换积分次序为 ( )A .⎰⎰2014),(ydxy x f dy B .⎰⎰2040),(ydx y x f dyC .⎰⎰1040),(ydx y x f dy D .⎰⎰1024),(ydxy x f dy4.若D 是由2x y =和2y x =所围成的区域,L 为区域D 的正向边界,则⎰-Ldxy dy x 222131= ( )A .143 B .91 C .41 D .52415.若L 是围成平面内一闭区域D 的正向边界曲线,则曲线积分⎰+Lxy dy x dx xe 2可化为二重积分 ( )A .⎰⎰-Dxy d x e x σ)2(2 B .⎰⎰-Dxy d e x x σ)2(2C .⎰⎰+Dxy xy d e x e σ)(2 D .⎰⎰-Dxy xy d e x e σ)(2四、解答题1.区域D 是由抛物线yx =,直线0=x 和0223=+-y x 围成,计算⎰⎰Dxdxdy 的值2.设}|),{(222π≤+=y x y x D ,求二重积分⎰⎰+Ddxdy y x 22sin3.计算dy y e dx y y e x Lx )1cos ()sin (-+-⎰,其中L是圆周x y x 422=+,且正向为逆时针方向4.求半径为R ,高为H )(R H <的球冠面积5.求两个底面半径相等的直交圆柱面222R y x =+与222R z x =+所围成的立体的体积。
重积分练习题含答案第十章重积分练习结论1:如果积分区域D 关于y 对称,}0,),(),{(1≥∈=x D y x y x D 则=--=-=DD y x f y x f d y x f y x f y x f d y x f 1),(),(),(2),(),(0),(时当时当σσ结论2:如果积分区域D 关于x 轴对称,}0,),(),{(1≥∈=y D y x y x D 则=--=-=DD y x f y x f d y x f y x f y x f d y x f 1),(),(),(2),(),(0),(时当时当σσ结论3:如果积分区域D 关于坐标原点O 对称,则=---=--=DD y x f y x f d y x f y x f y x f d y x f 1),(),(),(2),(),(0),(时当时当σσ其中}0,),(),{(1≥∈=x D y x y x D结论4:如果积分区域D 关于直线=y x 对称,则=DDd x y f d y x f σσ),(),(练习11.求σ-=??d x y I D2,其中2y 0,1x 1:D ≤≤≤≤-2.证明??-=xab abady y b y f dy y f dx ))(()((f 连续)3. 设)(x f 在区间],[b a 上连续,且0)(>x f ,试证明? ->b aba ab dx x f dx x f 2)()(1)(4.计算[]??++Ddxdy y x yf x )(122,其中D 由3x y =,1=y ,1-=x 围成。
5.计算vdv y x I )(22,v 是由yOz 平面上曲线z y 2=绕z 轴旋转所得平面2=z ,8=z 所围区域。
6. 设函数)(x f 连续,[]d v y x f zt F v++=)()(222,其中{}H z t yx z y x V ≤≤≤+=0,),,222(,试求dtdF 和2)(limtt F t →7. 求曲面221y x z ++=在点)3,1,1(0-M 的切平面与曲面22y x z +=所围立体的体积V8.设半径为R 的球面∑的球心在定球面)0(222>=++a a z y x 上,问当R 取何值时,∑在定球面内部的那部分1∑的面积最大?练习21.计算??Dxyd σ,其中区域D 是由抛物线12-=x y 及直线x y -=1所围成的区域-8272.计算??+Dyx d eσ,其中D 是由1≤+y x 所确定的区域 ??? ?-e e 13.计算??+Ddxdy y x )sin(,其中D 为正方形区域:ππ≤≤≤≤y x 0,0 )2(π4.更换积分次序① ??211),(x xdy y x f dx ② ??-π0sin sin2),(xx dy y x f dx5.计算由平面0,0,6===++y x z y x 及42=+y x 所围成的立体的体积 ??3646. 球体2222+x y z R +≤与Rz z y x 2222≤++的公共部分为一立体,求其体积3125R π7. 计算三重积分Ωzdxdydz ,其中Ω为由圆锥面的22yx z +=及平面1=z 所围成区域 ??4π8. 分别用柱面坐标、球面坐标和直角坐标计算三重积分Ω=zdv x I 2,其中Ω是由球面2222=++z y x 及圆锥面22y x z +=所围成(含z 轴部分) ??12π9. 求球面2222a z y x =++含在圆柱面ax y x =+2 2内部的那部分面积(0>a )))2(2(2-πa重积分练习一参考答案1.求σ-=d x y I D2,其中2y 0,1x 1:D ≤≤≤≤-解:如图,曲线2x y =把区域D 分为1D 和2D ,其中1x 1D 1≤≤-:,2x y 0≤≤;2y x,1x 1:D 22≤≤≤≤-σ-+σ-=σ-=d x y d y xd x y I 21D 2D 2D2()()??--=-?+-?=1122112221513xx dyx y dx dy y xdx2.证明??-=x ab abady y b y f dy y f dx ))(()((f 连续)证:左端=??xabady y f dx )(,??≤≤≤≤bx a x y a D ,作出积分域交换积分顺序,?? ≤≤≤≤by a b x y D左端==xab ady y f dx )(??by b adx y f dy )(?=-=b ady y b y f ))((右端,证毕!注:本题还可这样证明:令?--=t axat adx x t x f dy y f dx t F ))(()()(,证明0)(0)(=?='t F t F3.设)(x f 在区间],[b a 上连续,且0)(>x f ,试证明?->b abaa b dx x f dx x f 2)()(1)(证:设平面区域},),({b y a b x a y x D ≤≤≤≤=,D 关于直线x y =对称=∴b ab ab ady y f dx x f dx x f dx x f )(1)()(1)(222)()()()()(221)()()()(21)()()()(21)()()()(a b d x d y d x d yy f x f y f x f d x d y y f x f y f x f d x d y x f y f y f x f d x d y x f y f d x d y y f x f DDD DDD-==≥+=+==4.计算[]??++Ddxdy y x yf x )(122,其中D 由3x y =,1=y ,1-=x 围成。
重积分、第一类积分课外练习题1、利用重积分的几何意义求下列积分值.(1){}222,(,)|DD x y x y R σ=+≤;(2){}2,(,)|1,1,0Dd D x y x y y x y σ=+≤−≤≥∫∫.2、计算下列积分. (1){},(,)|1,1x yDed D x y x y σ+=≤≤∫∫;(2)2,Dx ydxdy D ∫∫由直线1,2y x ==及y x =所围成;(3)cos(),Dx x y dxdy D +∫∫是以点(0,0),(,0)π和(,)ππ为顶点的三角形区域;(4)211 0x dy dx ∫∫;(5)1sin , D ydxdy D y ∫∫是由22y x π=与y x =所围成.3、改变下列二次积分的积分顺序.(1) 10(,)xdx f x y dy ∫∫;(2)1221(,)(,)xx dx f x y dy dx f x y dy −+∫∫∫∫4、利用极坐标计算下列二重积分.(1)(4)Dx y dxdy −−∫∫,其中D 是圆域 222x y R +≤;(2)D,其中D 为上半圆域222x y ax +≤;(3)arctanDydxdy x∫∫,其中区域D 是由圆22224,1x y x y +=+=及直线0,y y x ==所围成的第一象限内的部分;(4)122 0 0)dx x y dy +∫∫.5、选择适当的坐标系计算下列二重积分.(1)D,其中D 是由圆周221x y +=及坐标轴所围成的在第一象限内的区域;(2)()22Dx y dxdy +∫∫,其中D 是由直线,,y x y x a y a ==+=及3y a =所围成的区域,其中0a >.6、已知区域D 是由抛物线22,(0)y px y qx p q ==<<与双曲线,xy a xy b ==所围成,其中0a b <<,试求D 的面积A .7、利用广义极坐标:cos ,sin (0,02,0,0)x ar y br r a b θθθπ==≥≤≤>>计算二重积分2Dx dxdy ∫∫,其中D 为椭圆域22221x y a b +≤.8、设[]()(,)f x C a b ∈,证明: 2 2()()()()b x baaadx x y f y dy b y f y dy −=−∫∫∫.9、证明不等式:2216121655x y ππ+≤≤≤∫∫. 答案:1、(1)223R π;(2) 2.2、(1) 21e e ⎛⎞−⎜⎟⎝⎠; (2)2915; (3)32π−; (4)1(1)3e −; (5)21π−3、 21 12 0(1)(,),(2)(,)y y y ydy f x y dx dy f x y dx −∫∫∫∫4、 23248233(1)2(2),(2),(3),(4)3323644R Ra a ππππ⎛⎞+−⎜⎟⎝⎠ 5、4(1)(2),(2)148a ππ− 16()ln 3q b a p−、 374a b π、1、计算下列重积分(1)zdxdydz Ω∫∫∫,Ω由曲面 z =及 1z =围成;(2)()x y z dxdydz Ω++∫∫∫,(){|0,0,0}x y z x a y z c bπΩ=++≤≤≤≤≤≤;(3) cos xy zdxdydz Ω∫∫∫,其中Ω为抛物柱面y =与平面0,0,2y z x z π==+=所围成的区域;(4) ()222x y z dxdydz Ω++∫∫∫,其中Ω是椭圆面 2222221x y z a b c++=的内部2、选择适当的坐标系计算下列三重积分: (1)Ω∫∫∫,Ω是由圆柱面 2220,0,0x y x y z +−=≥=与 ()0z a a =>所围成的; (2)zdxdydz Ω∫∫∫,Ω是由曲面 z =及z =所围成;(3)()22xy dxdydz Ω+∫∫∫,Ω是由 222x y z +=及 2z =所围成;(4)()22xy dxdydz Ω+∫∫∫,Ω是由 z z ==及 0z =所围成的区域,其中 0b a <<; (5)∫∫∫, Ω是由球面 2222x y z Rz ++=所围成的区域;(6)()32222sin x y zdxdydz Ω++∫∫∫,Ω是由锥面z =)a 0z =>所围成的;(7)()222222ln 11z x y z dxdydz x y zΩ++++++∫∫∫, ()222{,,|1}x y z x y z Ω=++≤;(8)222dxdydz x y z Ω++∫∫∫,Ω是2221x y z ++≥ 与2229x y z z ++≤的公共部分;(9)1dx∫∫∫;(10) ) 22 0aadx xy dz −+∫∫∫;(11) ()()2222236,{,,|1}94x y x y z dxdydz x y z z Ω++Ω=++≤∫∫∫3、设 ()3(,,)f x y z C R ∈,证明()()()1211ax by cz dxdydz u f ku du πΩ−++=−∫∫∫∫,其中222:1,0,0,0x y z k a b c Ω++≤=>>>答案:1、 22222224(1)();(3)2;(4)()4415abc bca acb abc a b c πππ++−++1;(2)22、 5581648(1);(3);(4)();(5)93155b a πππ−2a ;(2)8; 3280(6)(1cos )1;(7)0;(8);(9)3298a ππ⎛⎞−−⎜⎟⎜⎟⎝⎠;251864(10);(11)105a ππ1、计算下列曲线积分 (1)∫v 为圆周222x y y +=−;(2)()Lx y ds +∫是连接点(1,0)和点(0,1)的直线段;(3)22()Lx y ds +∫v 为圆周cos ,sin ,02x a t y a t t π==≤≤; (4)Lxyds ∫是抛物线22y x =上从原点到点(2,2)的那一段弧;(5)L是摆线(sin ),(1cos )x a t t y a t =−=−的第一拱,即对应于02t π≤≤的那一段弧;2、计算下列积分(1)222L ds x y z ++∫为曲线cos ,sin ,t t tx e t y e t z e ===从0到2的一段弧;(2) 2Lx yzds ∫为折线ABCD :(0,0,0),(0,0,2),(1,0,2),(1,3,2)A B C D ;答案:1、(1) 8;; (3) 32a π; (5) 23(2)a π.2、(1)2(1)2e −−;(2) 9.1、计算曲面积分(,,)f x y z dS Σ∫∫,其中Σ是抛物面222()z x y =−+,在xy 平面上方的部分,(,)f x y 分别如下:(1)(,,)1f x y z ≡;(2)22(,,)f x y z x y =+;(3)(,,)3f x y z z = 2、计算下列曲面积分(1)xyzdS Σ∫∫w ,其中Σ为四面体1,0,0,0x y z x y z ++≤≥≥≥的整个表面;(2)()xy yz xz dS Σ++∫∫,Σ为圆锥面z =被曲面222x y ax +=所割下的部分;(3)xyz dS Σ∫∫,其中Σ是22z x y =+被平面1z =所割下的部分;答案:1、(1)133π; (2)14930π; (3)11110π2、(1)120 (2)415a (3)1420−。
第九章 重积分A1、 填空题1)交换下列二次积分的积分次序(1)()=⎰⎰-dx y x f dy y y 102,______________________________________________ (2)()=⎰⎰dx y x f dy y y 2022,______________________________________________ (3)()=⎰⎰dx y x f dy y 100,_______________________________________________ (4)()=⎰⎰---dx y x f dy y y 101122,___________________________________________ (5)()=⎰⎰dy y x f dx ex 1ln 0,______________________________________________ (6)()()=⎰⎰---dx y x f dy y y 404214,________________________________________ 2)积分dy e dx xy ⎰⎰-2022的值等于__________________________________ 3)设(){}10,10,≤≤≤≤=y x y x D ,试利用二重积分的性质估计()σd y x xy I D⎰⎰+=的 值则 。
4)设区域D 是有x 轴、y 轴与直线1=+y x 所围成,根据二重积分的性质,试比较积分 ()σd y x I D 2⎰⎰+=与()σd y x I D 3⎰⎰+=的大小________________________________5)设()⎭⎬⎫⎩⎨⎧≤≤≤≤=20,20,ππy x y x D ,则积分()dxdy y x I D⎰⎰+-=2sin 1 ___________________________________________6)已知Ω是由12,0,0,0=++===z y x z y x 所围,按先z 后y 再x 的积分次序将 ⎰⎰⎰Ω=xdxdydz I 化为累次积分,则__________________________=I7)设Ω是由球面222y x z --=与锥面22y x z +=的围面,则三重积分dxdydz z y x f I ⎰⎰⎰Ω++=)(222在球面坐标系下的三次积分表达式为2、 把下列积分化为极坐标形式,并计算积分值1)⎰⎰-+a x ax dy y x dx 2020222)(2)⎰⎰+ax dy y x dx 00223、利用极坐标计算下列各题1)⎰⎰+D y x d e σ22,其中D 是由圆周122=+y x 及坐标轴所围成的在第一象限内的闭区域.2)⎰⎰++Dd y x σ)1ln(22,其中D 是由圆周122=+y x 及坐标轴所围成的在第一象限的闭区域.3)⎰⎰D d xy σarctan,其中D 是由圆周1,42222=+=+y x y x 及直线x y y ==,0所围成的在第一象限的闭区域.4、选用适当的坐标计算下列各题 1)⎰⎰D d yx σ22,其中D 是直线x y x ==,2及曲线1=xy 所围成的闭区域.2)⎰⎰+D yd x σsin )1(,其中D 是顶点分别为)2,1(),0,1(),0,0(和)1,0(的梯形闭区域.3)⎰⎰--D d y x R σ222,其中D 是圆周Rx y x =+22所围成的闭区域.4)⎰⎰+D d y x σ22,其中D 是圆环形闭区域{}2222),(b y x a y x ≤+≤.5、设平面薄片所占的闭区域D 由螺线θρ2=上一段弧⎪⎭⎫ ⎝⎛≤≤20πθ与直线2πθ=所围成,它的面密度为()22,y x y x +=μ,求这薄片的质量(图9-5).6、求平面0=y ,()0>=k kx y ,0=z ,以及球心在原点、半径为R 的上半球面所围成的在第一卦限内的立体的体积(图9-6).7、设平面薄片所占的闭区域D 由直线2=+y x ,x y =和x 轴所围成,它的面密度 ()22,y x y x +=μ,求该薄片的质量.8、计算由四个平面0=x ,0=y ,1=x ,1=y 所围成的柱体被平面0=z 及 632=++z y x 截得的立体的体积.9、求由平面0=x ,0=y ,1=+y x 所围成的柱体被平面0=z 及抛物面z y x -=+622 截得的立体的体积.10、计算以xoy 面上的圆周ax y x =+22围成的闭区域为底,而以曲面22y x z +=为顶的曲顶柱体的体积.11、化三重积分()⎰⎰⎰Ω=dxdydz z y x f I ,,为三次积分,其中积分区域Ω分别是1)由双曲抛物面z xy =及平面0,01==-+z y x 所围成的闭区域.2)由曲面222y x z +=及22x z -=所围成的闭区域.12、设有一物体,占有空间闭区域(){}10,10,10,,≤≤≤≤≤≤=Ωz y x z y x ,在点()z y x ,, 处的密度为()z y x z y x ++=,,ρ,计算该物体的质量.13、计算⎰⎰⎰Ωdxdydz z xy 32,其中Ω是由曲面xy z =,与平面1,==x x y 和0=z 所围成的闭区域.14、计算⎰⎰⎰Ωxyzdxdydz ,其中Ω为球面1222=++z y x及三个坐标面所围成的在第一卦限内的闭区域.15、算⎰⎰⎰Ωzdxdydz ,其中Ω是由锥面22y x Rh z +=与平面()0,0>>=h R h z 所围成的闭区域.16、利用柱面坐标计算三重积分⎰⎰⎰Ωzdv ,其中Ω是由曲面222y x z --=及22y x z +=所围成的闭区域.17、利用球面坐标计算三重积分()⎰⎰⎰Ω++dv z y x 222,其中Ω是由球面1222=++z y x 所围成的闭区域.18、选用适当的坐标计算下列三重积分1)⎰⎰⎰Ωxydv ,其中Ω为柱面122=+y x 及平面1=z ,0=z 0=x ,0=y 所围成的在第一卦限内的闭区域.2)⎰⎰⎰Ωdxdydz z 2,其中Ω是两个球2222R z y x ≤++和)0(2222>≤++R Rz z y x 的公共部分.3)()⎰⎰⎰Ω+dv y x 22,其中Ω是由曲面()222254y x z +=及平面5=z 所围成的闭区域.4)()⎰⎰⎰Ω+dv y x22,其中闭区域Ω由不等式A z y x a ≤++≤<2220,0≥z 所确定.19、利用三重积分计算下列由曲面所围成的立体的体积1)226y x z --=及22y x z +=.2)()02222>=++a az z y x 及222z y x =+(含有z 轴的部分).20、球心在原点、半径为R 的球体,在其上任意一点的密度大小与这点到球心的距离成正比,求这球体的的质量.21、求球面2222a z y x =++含在圆柱面ax y x =+22内部的那部分面积.22、求锥面22y x z +=被柱面x z 22=所割下部分的曲面面积.23、求由抛物线2x y =及直线1=y 所围成的均匀薄片(面密度为常数μ)对于直线1-=y 的转动惯量.24、设薄片所占的闭区域D 如下,求均匀薄片的质心 D 是半椭圆形闭区域()⎭⎬⎫⎩⎨⎧≥≤+0,1,2222y b y a x y x .25、设平面薄片所占的闭区域D 由抛物线2x y =及直线x y =所围成,它在点()y x ,处的面密度()y x y x 2,=μ,求该薄片的质心.25、利用三重积分计算下列由曲面所围立体的质心(设密度1=ρ)1)222y x z +=,1=z2)222y x A z --=,222y x a z --=()0>>a A ,0=z26、求半径为a 高为h 的均匀圆柱体对于过中心而平行于母线的轴的转动惯量(设密度1=ρ).B1、 根据二重积分的性质,比较下列积分的大小1)()σd y x D ⎰⎰+2与()σd y x D⎰⎰+3,其中积分区域D 是由圆周()()21222=-+-y x 所围成.2)()σd y x D ⎰⎰+ln 与()[]σd y x D⎰⎰+2ln ,其中D 是三角形闭区域,三顶点分别为()0,1, ()1,1,()0,2 .2、计算下列二重积分1)⎰⎰+σd e y x ,其中(){}1,≤+=y x y x D2)()⎰⎰-+D d x y x σ22,其中D 是由直线2=y ,x y =及x y 2=所围成的闭区域3),()σd y x y D ⎰⎰+-+9632,其中(){}222,R y x y x D ≤+=3、化二重积分()σd y x f I D⎰⎰=,为而次积分(分别列出对两个变量先后次序不同的两个二次积分),其中积分区域D 是 1)由x 轴及半圆周222ry x =+()0≥y 所围成的闭区域2)环形闭区域(){}41,22≤+≤y x y x4、求由曲面222y x z +=及2226y x z --=所围成的立体的体积.5、计算()⎰⎰⎰Ω+++31z y x dxdydz ,其中Ω为平面0=x ,0=y ,0=z ,1=++z y x 所围成的四面体.6、计算下列三重积分 1)dxdydz z ⎰⎰⎰Ω2,其中Ω是两个球:2222R z y x ≤++和Rz z y x 2222≤++()0>R 的公共部分.2)()dv z y x z y x z ⎰⎰⎰Ω++++++11ln 222222,其中Ω是由球面1222=++z y x 所围成的闭区域.3)()d v z y⎰⎰⎰Ω+22,其中Ω是由xoy 平面上曲线x y 22=绕x 轴旋转而成的曲面与平面5=x 所围成的闭区域.7、设球体占有闭区域(){}Rz z y x z y x 2,,222≤++=Ω,它在内部各点处的密度的大小等于该点到坐标原点的距离的平方,试求这球体的球心.8、一均匀物体(密度ρ为常量)占有的闭区域Ω由曲面22y x z +=和平面0=z ,,a x =a y =所围成1)求物体的体积; 2)求物体的质心;3)求物体关于z 轴的转动.C1、利用二重积分的性质,估计积分()⎰⎰++=Dd y x I σ10,其中D 是由圆周422=+y x 所围成.2、用二重积分计算立体Ω的体积V ,其中Ω由平面0=z ,x y =,a x y +=,a y 2=和y x z 23+=所围成()0>a .3、计算二重积分⎰⎰Dydxdy ,其中D 是由直线2-=x ,0=y 以及曲线22y y x --=所围成的平面区域.4、设()y x f ,在积分域上连续,更换二次积分()⎰⎰---=yy dx y x f dy I 311102,的积分次序.5、计算二重积分dxdy x y I D⎰⎰-=2,其中积分区域D 是由20≤≤y 和1≤x 确定.6、求二重积分()dxdy xe y D y x ⎰⎰⎥⎦⎤⎢⎣⎡++22211的值,其中D 是由直线x y =,1-=y 及1=x 围成的平面区域. 7、计算⎰⎰⎰Ωdv z 2,其中Ω由曲面2222R z y x =++及()2222R r z y x =-++围成.8、计算dxdydz z xy I ⎰⎰⎰Ω=32,其中Ω是由曲面xy z =与平面1=y 及0=z 所围成的闭区域.9、设有一半径为R 的球体,0P 是此球表面上的一个定点,球体上任一点的密度与该点到0P 的距离的平方成正比(比例常数0>k ),求球体的重心的位置. 10、设有一高度为()t h (t 为时间)的雪堆在融化过程中,其侧面满足方程()()()t h y x z t h z 22+-=(设长度单位为cm ,时间单位为h ),已知体积减少的速率与侧面积成正比例(比例系数9.0),问高度为130(cm )的雪堆全部融化需多少时间?第九章 重积分答案 习 题 答 案(A )1、 填空题 1)①()()⎰⎰⎰⎰-+2120122,,x x dy y x f dx dy y x f dx②()dy y x f dx xx ⎰⎰240, ③()dy y x f dy x⎰⎰110, ④()dy y x f dx x ⎰⎰--21011,⑤()⎰⎰ee ydx y x f dy ,10⑥()⎰⎰-+-244202,x x dy y x f dx2)()4121--e 3)20≤≤I 4)()()⎰⎰⎰⎰+≥+D Dd y x d y x σσ325)2-π 6)⎰⎰⎰---yx x xdz dy dx 21021017)()⎰⎰⎰2224020sin dr r r f d d ϕϕθππ2、1)443a π 2)()[]21ln 2613++a3、1)()14-e π2)()12ln 24-π 3)2643π4、1)49 2)2sin 22cos 1sin 1cos 23--++ 3)⎪⎭⎫ ⎝⎛-34313πR 4)()3332a b -π 5、5401π 6、k R arctan 313 7、34 8、27 9、617 10、4323a π 11、1)()dz z y x f dy dx xy x⎰⎰⎰-01010,, 2)()⎰⎰⎰-+----22222221111,,x y x x x dz z y x f dy dx12、23 13、3641 14、481 15、224R h π 16、π127 17、π54 18、1)81 2)548059R π 3)π8 4)()55154a A -π19、1)π332 2)3a π 20、3R k π 21、()222-πa22、π2 23、μ105368=I 24、π34,0by x == 25、4835=x ,5435=y 26、⎪⎭⎫ ⎝⎛43,0,027、M a 221(ρπh a M 2=为圆柱体的质量) (B )1、 1)()()⎰⎰⎰⎰+≤+DDd y x d y x σσ32 2)()()⎰⎰⎰⎰+≤+DDd y x d y x σσln ln 22、1)1--e e 2) 613 3) 2494R R ππ+ 3、1)()⎰⎰--=220,x r rr dy y x f dx I ,()⎰⎰---=2222,0y r y r rdx y x f dy I2)()()()⎰⎰⎰⎰⎰⎰-------------++=222222141141114412,,,x x x x x x dy y x f dx dy y x f dx dy y x f dx I()⎰⎰---+224421,x x dy y x f dx()()()⎰⎰⎰⎰⎰⎰-----------++=222222144111114421,,,y y y y y y dx y x f dy dx y x f dy dx y x f dy I()⎰⎰-----+224412,y y dx y x f dy4、π65、⎪⎭⎫ ⎝⎛-852ln 21 ; 6、1)548059R π 2)0 3)π3250 ; 7、⎪⎭⎫ ⎝⎛R 45,0,0 8、1)438a 2)⎪⎭⎫ ⎝⎛2157,0,0a 3)645112a ρ(C )1、 解:令()10,++=y x y x f ,关键是求()y x f ,在D 上的最大值和最小值,在D 内部,1=x f ,1=y f ,因此()y x f ,在D 内部无驻点,最值点一定在边界上取得,作 ()()410,22-++++=y x y x y x F λ由方程组⎪⎩⎪⎨⎧=-+='=+='=+='0402102122y x F y F x F y x λλλ解得驻点为()2,2,()2,2-,比较可得最小值2210-=m ,最大值为2210+=M ,而D 的面积为π4,由估值定理得()()258258+≤≤-ππI 。
高等数学课程第十章 重积分试卷单元测试题(A )一、选择题(每小题4分,共20分)1、()()01,lim ,niiii Df x y d f λσξησ→==∆∑⎰⎰中λ是 ( )A. 最大小区间长B. 小区域最大面积C. 小区域直径D. 小区域最大直径2、函数(),f x y 在有界闭区域 D 上有界,是二重积分(),Df x y dxdy ⎰⎰存在的 ( )A. 充分必要条件B. 充分条件,但非必要条件C. 必要条件,但非充分条件D. 既非充分又非必要条件3、二重积分Dxydxdy ⎰⎰(其中2:0,01D y x x ≤≤≤≤)的值为 ( )A.16 B.112 C. 12D. 144、若区域 ()22:11D x y -+≤,则二重积分 化为累次积分为 ( ) A.()2cos 0cos ,sin d f r r rdr πθθθθ⎰⎰B.()2cos 0cos ,sin d f r r rdr πθπθθθ-⎰⎰C.()2cos 202cos ,sin d f r r rdr πθπθθθ-⎰⎰D.()2cos 22cos ,sin d f r r rdr πθθθθ⎰⎰5、设空间区域02222≥≤++Ωz R z y x ,:;00022221≥≥≥≤++Ωz y x R z y x ,,,:,则 ( ) A.1d d d 4d d d x x y z x x y z ΩΩ=⎰⎰⎰⎰⎰⎰ B.1d d d 4d d d y x y z y x y z ΩΩ=⎰⎰⎰⎰⎰⎰C.1d d d 4d d d z x y z z x y z ΩΩ=⎰⎰⎰⎰⎰⎰ D.1d d d 4d d d xyz x y z xyz x y z ΩΩ=⎰⎰⎰⎰⎰⎰6. 更换积分I=10(,)ydy f x y dx ⎰⎰的次序,则I= ( )A. ⎰⎰101),(xdy y x f dx ; B.110(,)dx f x y dy ⎰⎰; C.10(,)xdx f x y dy ⎰⎰; D.11(,)ydx f x y dy ⎰⎰.7. 若10,10:≤≤≤≤y x D ,则积分⎰⎰+Ddxdy y x )(= ( )A. 1;B. 2;C. 0;D. -1.8. 二重积分2Dxy dxdy ⎰⎰(其中2:0,2D y x x ≤≤≤)的值为 ( ) A. 0; B.323; C. 643; D. 256.二、判断题(每小题2分,共10分)1、如果函数(),f x y 在有界闭区域D 上连续,则其在D 上可积. ( ) 2. 如果函数(),f x y 在有界闭区域D 上可积,k 是常数则()(),,DDkf x y d k f x y d σσ=⎰⎰⎰⎰.( )3、若函数(),f x y 是有界闭区域D 上的负连续函数,则(),0Df x y d σ<⎰⎰ . ( )4、如果在D 上,(),1f x y ≡-,D 的面积为 σ,则Dd σσ=⎰⎰ . ( )5、如果函数(),f x y 在关于y 轴对称的有界闭区域D 上连续,且()(),,f x y f x y -=-,则(),0Df x y =⎰⎰ .( )三、填空题(每小题4分,共20分)1、设区域D 的面积为S ,则2Dd σ⎰⎰= .2、设222:D x y a +≤,0y ≥,m 为奇数,则m nDx y dxdy =⎰⎰ . 3、已知(),f x y 为连续函数,则()1,ydy f x y dx ⎰交换积分次序后 .4、二次积分()1,dx f x y dy ⎰在极坐标系下先对r 积分为 .5、根据二重积分的几何意义,D= 其中22:4D x y +≤,0y ≥。