4欧式期权定价BS方法delta值和隐含波动率计算

金融衍生品定价中的隐含波动率计算技术使用教程隐含波动率是金融衍生品定价中至关重要的指标之一。

它是指根据市场价格来估计未来波动率的一种方法。

隐含波动率计算技术被广泛应用于金融市场，特别是在期权交易中。

本文将向您介绍隐含波动率的概念、计算方法和常用的计算工具。

1.隐含波动率的概念和意义隐含波动率是指在给定期权合约的市场价格基础上，通过反向计算得出的一种估计未来波动率的方法。

它反映了市场对未来波动率的预期情况。

隐含波动率的计算对于定价衍生品合约非常重要，因为它可以帮助交易者判断市场对于未来波动率的预期，从而更好地制定交易策略。

2.隐含波动率的计算方法隐含波动率的计算方法主要基于期权的定价模型，其中最常用的模型是布莱克-斯科尔斯期权定价模型（Black-Scholes option pricing model）。

布莱克-斯科尔斯模型是一种计算欧式期权的理论定价模型，它假设市场有一个风险中性的概率分布，并以此计算期权的公平价格。

在布莱克-斯科尔斯模型中，期权的价格与标的资产价格、行权价格、到期时间、无风险利率和隐含波动率等因素有关。

通过使用布莱克-斯科尔斯模型，可以利用已知的市场价格来反向推导出对应的隐含波动率。

这可以通过不断调整隐含波动率的值，使得模型计算出的价格与市场价格相匹配。

除了布莱克-斯科尔斯模型之外，还有其他一些期权定价模型，如考虑了波动率微笑曲线的扩散模型、随机波动率模型等。

这些模型也可以用于计算隐含波动率，但在实际应用中，布莱克-斯科尔斯模型被广泛使用。

3.常用的隐含波动率计算工具在金融市场中，有很多工具可以帮助交易者计算隐含波动率。

以下是一些常用的工具：- 期权交易平台：大多数期权交易平台都提供了隐含波动率计算的功能。

交易者可以通过输入期权合约的相关参数，如标的资产价格、行权价格、到期时间等，来计算得到隐含波动率。

- 金融数据供应商：一些金融数据供应商如彭博（Bloomberg）和汤森路透（Thomson Reuters）也提供了隐含波动率的计算服务。

金融计算中的隐含波动率计算原理隐含波动率是金融市场中一个重要的概念，它是指根据期权市场价格反推出的预期波动率。

在金融计算中，隐含波动率的计算原理是一项关键的技术，它在期权定价、风险管理和投资决策中具有重要的应用价值。

隐含波动率计算的原理基于期权定价模型，其中最常用的是布莱克-斯科尔斯期权定价模型。

该模型基于假设，认为市场上的期权价格是合理的，即不存在套利机会。

根据这个假设，布莱克-斯科尔斯模型可以通过期权价格来计算出隐含波动率。

在计算隐含波动率时，首先需要获取市场上的期权价格。

期权价格是由期权的买卖双方在市场上自由决定的，它受到多种因素的影响，包括标的资产价格、行权价、剩余到期时间、无风险利率和隐含波动率等。

通过观察市场上的期权价格，我们可以得到一个波动率曲面，即不同行权价和剩余到期时间下的隐含波动率。

在计算隐含波动率时，需要使用期权定价模型来进行逆推。

布莱克-斯科尔斯模型是一个基于偏微分方程的数学模型，它可以根据期权价格、标的资产价格、行权价、剩余到期时间、无风险利率和隐含波动率等参数，计算出期权的理论价格。

通过不断尝试不同的隐含波动率值，将计算出的理论价格与市场上的实际价格进行比较，可以找到与市场价格最接近的隐含波动率。

隐含波动率的计算是一个迭代的过程，需要不断调整隐含波动率的值，直到计算出的理论价格与市场价格之间的误差足够小。

这个过程可以通过数值方法来实现，例如二分法、牛顿法或蒙特卡洛模拟等。

这些方法可以在较短的时间内快速计算出隐含波动率，为金融市场参与者提供了重要的参考信息。

隐含波动率的计算原理在金融市场中具有广泛的应用。

首先，它可以用于期权定价。

期权的价格与隐含波动率密切相关，通过计算隐含波动率，可以得到一个合理的期权价格，帮助投资者进行决策。

其次，隐含波动率还可以用于风险管理。

投资组合的风险水平与波动率密切相关，通过计算隐含波动率，可以对投资组合的风险进行评估和控制。

此外，隐含波动率还可以用于投资决策。

Black—Scholes 模型波动率某变量在单位时间内连续复利收益率的标准差σ被定义为这一变量的波动率期权。

当波动率被用于期权定价时时间单位通常定义为一年，因此波动率就是一年的连续复利收益率的标准差；但当波动率被用于风险控制时，时间单位通常是一天，此时的波动率对应于没天的连续复利收益率的标准差。

一般来讲，σ√T等于变量ln(S TS0)的标准差这里的S T为市场变量在时间T的价格，S0是此市场变量的当前价格，表达式ln(S TS0)等于变量在时间T的连续复利收益率（这里的收益并不对应于单位时间收益）。

当σ对应于每天的波动率，T就应该以天来计算；当σ对应于每年的波动率，T就应以年来计量。

当所考虑的时间展望期较为短暂时，以标准差计量的将来股票价格的不确定性与我们展望期限的平方根成正比。

例如，股票价格4周变化的标准差近似等于每周变化的标准差的两倍，这一结论也就是著名的格言“不确定性与时间的平方根成正比”。

在计算波动率时，会产生以下问题，我们应该采用日历天数还是交易天数。

研究人员已经证明在交易开盘交易时的波动率比交易所关闭时的波动率要大很多，因此，当有历史数据估计波动率时，分析员常常忽略交易所关闭的天数，在计算时通常假定每年有252个交易日。

假设σy为某一资产的年波动率，σd为相应的日波动率，连续复利收益率的标准差分别为σy和σd√252，即σy=σd√252或σd=σ√252以上关系式说明，日波动率大约为年波动率的6%。

隐含波动率期权公式中唯一不能直接就是股票价格的波动率，隐含波动率是交易员从期权价格中计算出的隐含的波动率。

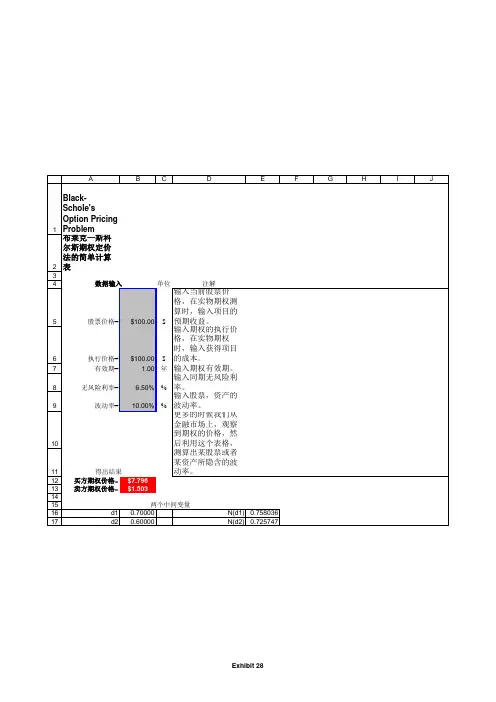
为了解释如何计算隐含波动率，我们假设某股票价格为21美元，期权行使价格为20美元，无风险利率为10%，期权期限为3个月，期权类型为欧式看涨期权，标的资产不支付任何股息，期权的市场价值为1.875美元，隐含波动率是对应于c=1.875时，Black-Scholes公式中σ的取值。

不幸的是，我们不能直接反解Black-Scholes公式并将波动率表示为期权价格以及其他变量的函数，但是我们可以用迭代的方式来丘吉尔隐含波动率。

BS模型及违约距模型公式BS模型是迄今为止应用较广且较为成熟的股票定价模型之一，其全名为Black-Scholes-Merton模型，是由费雪-布莱克、默顿-斯科尔斯共同独立发现并推导的，能够用来计算欧式期权（European Option）的理论价格。

BS模型最初应用于股票期权的定价和交易策略，但后来也被广泛应用于其他金融工具的定价和风险管理中。

根据BS模型，欧式期权的理论价格由五个变量决定：标的资产价格（S），行权价格（K），无风险利率（r），标的资产的波动率（σ），以及期权到期时间（t）。

BS模型将期权定价问题转化为一个偏微分方程求解问题，该方程即为著名的Black-Scholes方程，表达式如下：$\frac{1}{2}\sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS\frac{\partial V}{\partial S} + \frac{\partial V}{\partial t}- rV = 0$其中，V为期权的价格。

由于BS模型是个复杂的非线性偏微分方程，并且具有封闭解的限制，因此通常采用数值方法，如有限差分法或蒙特卡洛模拟等，来求解BS方程并计算期权的理论价格。

违约距模型（Distance-to-Default Model）是一种衡量公司违约风险的模型，用于评估公司违约可能性和违约损失的大小。

违约距（distance-to-default）指的是公司当前净资产价值与其违约边界之间的差距。

当违约距小于等于0时，该公司被认为处于违约状态。

违约距模型的公式可以有多种形式，根据不同的内含假设和数据可获得不同的模型。

其中，常见的一种违约距模型公式是基于Merton模型（也称为公司债务默认模型）的基础上建立的。

该模型首次由Robert Merton于1974年提出，主要基于了股票价格和债券价格之间的关系。

Merton模型假设公司负债不可调整，公司价值遵循几何布朗运动的随机过程，违约发生的条件是公司资产价值（V）首次小于债务偿付额（F）。

实验四隐含波动率计算隐含波动率是金融市场中一个重要的概念，用于衡量市场对未来波动性的预期。

它是根据期权定价模型计算得出的，主要用于期权交易之中。

在本次实验中，我们将学习如何使用Black-Scholes模型来计算隐含波动率。

Black-Scholes模型是一个用于计算期权价格的数学模型，它假设市场中没有套利机会，并且期权价格服从随机漫步的几何布朗运动。

在这个模型中，隐含波动率是一个未知的参数，我们需要通过已知的市场数据来计算得到。

首先，我们需要收集市场上的一些数据，包括期权的价格，标的资产的当前价格，以及期权到期时间等。

然后，我们可以使用Black-Scholes模型来计算出该期权的理论价格。

在这个计算过程中，我们需要假设一个初值的波动率，然后通过不断迭代的方式，将计算出的理论价格与市场价格进行比较，直到两者之间的差异达到最小值。

在实际计算中，我们可以使用不同的数值计算方法，如二分法、牛顿法等。

这些方法可以帮助我们快速地找到隐含波动率的近似解。

隐含波动率的计算结果可以帮助投资者判断市场对未来波动性的预期。

如果隐含波动率较高，意味着市场对未来波动性的预期较大，投资者可能需要采取相应的风险管理措施。

相反，如果隐含波动率较低，意味着市场对未来波动性的预期较小，投资者可以考虑采取一些策略来进行风险对冲或套利操作。

总结来说，隐含波动率是金融市场中一个重要的概念，它是通过Black-Scholes模型计算得出的。

隐含波动率的计算可以帮助投资者判断市场对未来波动性的预期，并采取相应的投资策略。

在实际操作中，我们可以使用不同的数值计算方法来计算隐含波动率的近似解。

欧式看涨期权计算公式
欧式看涨期权是一种金融衍生品，它允许投资者在期权到期日之前购买某种资产，以获得潜在的收益。

欧式看涨期权的计算公式是：
期权价值=max（0，标的价格-行权价格）
其中，标的价格是指期权到期日当天的标的资产价格，行权价格是指期权持有
人可以在期权到期日之前购买标的资产的价格。

欧式看涨期权的价值取决于标的价格和行权价格之间的差值，如果标的价格高
于行权价格，则期权价值为标的价格与行权价格之间的差值；如果标的价格低于行权价格，则期权价值为0。

欧式看涨期权的价值受到许多因素的影响，包括标的资产的价格波动、期权到
期日的距离、期权的行权价格以及市场的风险偏好等。

因此，投资者在投资欧式看涨期权时，应该考虑这些因素，以便更好地把握投资机会，获得更高的收益。

总之，欧式看涨期权的计算公式是：期权价值=max（0，标的价格-行权价格），它受到许多因素的影响，投资者在投资欧式看涨期权时，应该考虑这些因素，以便更好地把握投资机会，获得更高的收益。

bs模型计算公式BS模型又称为布莱克-斯科尔斯模型（Black-Scholes model），是一种用于计算欧洲期权价格的数学模型。

它是由费希尔·布莱克（Fischer Black）、默顿·斯科尔斯（Myron Scholes）和罗伯特·马顿（Robert Merton）于1970年提出。

BS模型基于一些假设，如市场效率、股票价格的几何布朗运动、无风险利率等，通过对期权和股票组合进行对冲交易，从而得出期权的正确定价。

BS模型的计算公式如下：C=S*N(d1)-X*e^(-r*T)*N(d2)P=X*e^(-r*T)*N(-d2)-S*N(-d1)其中，C表示期权的看涨定价，P表示期权的看跌定价。

S表示标的资产的现价，X表示期权的执行价格，r表示无风险利率，T表示期权到期时间。

N(代表标准正态分布的累积分布函数。

d1和d2的计算公式如下：d1 = (ln(S/X) + (r + 0.5 * sigma^2) * T) / (sigma * sqrt(T)) d2 = d1 - sigma * sqrt(T)其中，sigma表示标的资产的波动率。

波动率是BS模型中的一个重要参数，通常需要根据历史数据或市场预期进行估计。

用于计算d1和d2的sigma应该是年化波动率。

BS模型的核心思想是对冲交易，即构建一个期权和标的资产的组合，使其不受市场波动的影响，从而消除了市场风险，只保留了无风险利率的影响。

通过对冲交易，可以使用风险中性的概率测度，将未来的现金流折现到当前时刻，得到期权的正确定价。

BS模型在计算期权价格时使用了一些理论前提和假设，比如市场效率、收益率的对数正态分布等。

这些假设可能与实际情况有所偏差，因此BS模型的应用也存在一定的局限性。

在实际应用中，需要根据具体情况对模型进行调整和修正，以提高对期权价格的准确度和可靠性。

总之，BS模型是一种用于计算欧洲期权价格的数学模型，通过对期权和标的资产的对冲交易，消除了市场风险，保留了无风险利率的影响，从而得出期权的正确定价。

第四讲BS期权定价模型统计与管理学院第四讲BS期权定价模型第一节BS期权定价模型的基本思路第二节BS期权定价公式第三节BS期权定价公式的精确度评价与拓展第一节BS期权定价模型的基本思路股票价格服从的随机过程由It ô引理可得期权价格相应服从的随机过程dS Sdt SdWm s =+222212f f f fdf S S dt SdWS t S S m s s æö¶¶¶¶÷ç÷=+++ç÷ç÷綶¶¶èø第一节BS期权定价模型的基本思路BS微分方程BS期权定价公式222212f f frS S rft S S s ¶¶¶++=¶¶¶()()()12r T t c SN d Xe N d --=-第二节BS期权定价公式一、模型基本假设二、BS方程的推导三、风险中性定价原理四、BS期权定价公式的推导五、BS期权定价公式的参数估计一、假设证券价格遵循几何布朗运动，即µ和σ为常数 允许卖空标的证券没有交易费用和税收，所有证券都完全可分 衍生证券有效期内标的证券没有现金收益支付 不存在无风险套利机会证券交易是连续的，价格变动也是连续的衍生证券有效期内，无风险利率r为常数二、BS微分方程的推导由于假设股票价格S遵循几何布朗运动，因此在一个小的时间间隔∆t中，S的变化值∆S为dS Sdt SdWm s =+S S t S Wm s D =D +D二、BS微分方程的推导设f是依赖于S的衍生证券的价格，则f一定是S 和t的函数，根据伊藤引理可得：在一个小的时间间隔∆t中，f的变化值∆f满足：222212f f f f df S S dt SdW S t S S m s s æö¶¶¶¶÷ç÷=+++ç÷ç÷綶¶¶èø222212f f f f f S S t S W S t S S m s s æö¶¶¶¶÷ç÷D =++D +D ç÷ç÷綶¶¶èø二、BS微分方程的推导为了消除风险源∆W，可以构建一个包括一单位衍生证券空头和单位标的证券多头的组合。

资金计算期权交易的Delta值计算在金融交易领域中，资金计算期权交易是一种重要的交易策略。

而Delta值作为衡量期权对标的资产价格变动的敏感性指标，对于交易者来说具有至关重要的意义。

本文将介绍资金计算期权交易的Delta值计算方法，以帮助读者更好地理解和应用这一指标。

一、什么是资金计算期权交易资金计算期权交易是指利用期权合约进行交易，通过买入或卖出期权合约来获得价差的利润。

交易者不直接购买或持有标的资产，而是以期权合约为工具进行投机和对冲。

资金计算期权交易的目的是利用期权的杠杆效应，实现更高的利润率。

二、Delta值的概念Delta值是指期权合约价格相对于标的资产价格的变化率。

它反映了期权价格对标的资产价格变动的敏感程度。

对于看涨期权而言，Delta值介于0和1之间；对于看跌期权而言，Delta值介于-1和0之间。

当Delta值为1时，期权合约价格与标的资产价格完全一致；当Delta值为0时，期权合约价格与标的资产价格没有关联性。

三、资金计算期权交易的Delta值计算方法资金计算期权交易中的Delta值计算需要考虑到期权的合约乘数以及持有的期权合约数量。

下面分别介绍看涨期权和看跌期权的Delta值计算方法。

1. 看涨期权的Delta值计算方法看涨期权的Delta值计算公式为：Delta = 合约乘数 * 持有的看涨期权合约数量其中，合约乘数是指每个期权合约对应的标的资产数量。

持有的看涨期权合约数量是指交易者现阶段持有的看涨期权合约份数。

2. 看跌期权的Delta值计算方法看跌期权的Delta值计算公式为：Delta = 合约乘数 * 持有的看跌期权合约数量 * (-1)与看涨期权不同的是，看跌期权的Delta值为负数，需要将结果乘以-1。

四、资金计算期权交易中Delta值的应用Delta值作为衡量期权对标的资产价格变动敏感性的指标，对于交易者来说具有重要的参考价值。

通过观察和计算Delta值，交易者可以更好地了解期权价格与标的资产价格的关联性。

BS期权定价公式Black-Scholes 期权定价模型⼀、Black-Scholes 期权定价模型的假设条件Black-Scholes 期权定价模型的七个假设条件如下：1. 风险资产（Black-Scholes 期权定价模型中为股票），当前时刻市场价格为S 。

S 遵循⼏何布朗运动，即dz dt SdS σµ+=。

其中，dz 为均值为零，⽅差为dt 的⽆穷⼩的随机变化值（dt dz ε=，称为标准布朗运动，ε代表从标准正态分布（即均值为0、标准差为1的正态分布）中取的⼀个随机值），µ为股票价格在单位时间内的期望收益率，σ则是股票价格的波动率，即证券收益率在单位时间内的标准差。

µ和σ都是已知的。

简单地分析⼏何布朗运动，意味着股票价格在短时期内的变动（即收益）来源于两个⽅⾯：⼀是单位时间内已知的⼀个收益率变化µ，被称为漂移项，可以被看成⼀个总体的变化趋势；⼆是随机波动项，即dz σ，可以看作随机波动使得股票价格变动偏离总体趋势的部分。

2．没有交易费⽤和税收，不考虑保证⾦问题，即不存在影响收益的任何外部因素。

3. 资产价格的变动是连续⽽均匀的，不存在突然的跳跃。

4. 该标的资产可以被⾃由地买卖，即允许卖空，且所有证券都是完全可分的。

5. 在期权有效期内，⽆风险利率r 保持不变，投资者可以此利率⽆限制地进⾏借贷。

6．在衍⽣品有效期间，股票不⽀付股利。

7．所有⽆风险套利机会均被消除。

⼆、Black-Scholes 期权定价模型（⼀）B-S 期权定价公式在上述假设条件的基础上，Black 和Scholes 得到了如下适⽤于⽆收益资产欧式看涨期权的Black-Schole 微分⽅程：rf Sf S S f rS t f =??+??+??222221σ其中f 为期权价格，其他参数符号的意义同前。

通过这个微分⽅程，Black 和Scholes 得到了如下适⽤于⽆收益资产欧式看涨期权的定价公式：)()(2)(1d N Xe d SN c t T r ---=其中，t T d tT t T r X S d t T t T r X S d --=---+=--++=σσσσσ12221))(2/()/ln())(2/()/ln(c 为⽆收益资产欧式看涨期权价格；N （x ）为标准正态分布变量的累计概率分布函数（即这个变量⼩于x 的概率），根据标准正态分布函数特性，我们有)(1)(x N x N -=-。