简单环形网络的潮流计算
- 格式:doc
- 大小:4.15 MB
- 文档页数:20




66.第四章第三节:简单电网潮流计算(二)
4.3.3简单输电系统的潮流计算
简单输电系统一般包括开式网和环网。
开式电力网是一种简单的电力网,可分成无变压器的同一电压等级的开式网与有变压器的多级电压开式网。
每一种又包括有分支的开式网与无分支的开式网两种。
开式网的负荷一般以集中负荷表示,并且在计算中总是作为已知量。
1.同一电压等级开式网计算
进行开式网的计算首先要给定一个节点的电压,称为已知电压。
由于已知电压的节点不同,计算的步骤略有差别。
若已知开式网的末端电压,则由末端逐段向首端推算。
电力网计算中往往已知首端电压及各个集中负荷。
此时仅能采用近似计算方法。
(1)已知末端电压和各负荷点的负荷量,求首端电压
1)设末端电压为参考电压,计算从末端开始的第Ⅰ段线路中末端电纳中的功率损耗。
2)确定电源送往末端的负荷。
等于末端负荷与末端电纳功率损耗之和。
3)求第Ⅰ段线路阻抗中的电压降及功率损耗。
4)确定第Ⅰ段线路的首端电压
(2)已知首端电压和各负荷点的负荷量,求末端电压。
1)假定各点电压等于额定电压。
2)计算各负荷点对地电纳中的功率损耗。
3)将各负荷点对地电纳中的功率损耗与接在同一节点的负荷合并。
4)从第Ⅰ段线路开始,计算阻抗上的功率损耗以及由前一负荷点送出的功率。
5)电源点的总负荷应是电源点送出的负荷与电源线路首端电纳中功率损耗之和。
6)以电源点为参考电压,由电源线路开始逐段计算线路电压降。


关于环网潮流调整控制若干方法的探讨 Discussion on the control of loop power flow李剑锋韶关仁化供电局,广东韶关,512300摘要:电力作为国家的能源支柱和经济命脉,在国民经济的可持续发展中起着至关重要不可替代的作用。
电力系统潮流控制的研究已经成为世界各国电力系统长期发展中的关键研究课题。
本文基于潮流计算,阐述了几种潮流调整控制的方法。
关键词:潮流计算;调整;控制;探讨1.引言1.1电力系统接线方式尽管现实生活中的电力系统接线往往十分复杂,但其接线方式仍然可以分为开式网络、环形网络以及两端供电网络。
其中,开式网络又可以分为有备用和无备用的放射式、干线式、链式网络。
具体分类如图示图1开式网络(a)无备用方式;(b)有备用方式1.2潮流计算潮流控制的前提是潮流计算,只有计算出各节点、各支线的相关参数,才能对这个网络进行有效的潮流控制。
环形网络潮流计算虽然非常复杂,但是计算思想与开式网络大致相同,无论是用高斯-赛德尔法、牛顿-拉夫逊法还是P-Q 分解法,其核心都是对修正方程式的求解。
以一个n 节点的网络为例,我们不妨依次编号为1,2,3….,n ,其中一个平衡节点,m-1个PQ 节点,n-m 个PV 节点,那么应用牛顿-拉夫逊极坐标潮流计算的方法,建立的修正方程式为下式(1-1):⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∆∆∆∆∆∆n p P P Q P Q P 2211=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡→-←→-← )()1(2221122112222222121222222212111121211111112121111m n m nn np n n n n pn pp p p p p n p n p n p n pH H N H N H H H N H N H J J L J L J H H N H N H J J L J L J H H N H N H ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∆∆∆∆∆∆n pU U U U δδδδ 222111// (1-1)其中: jiij P H δ∂∂=; j j iij U U P N ∂∂=; j iij Q J δ∂∂=; j jiij U U Q L ∂∂=设置一组电压初值)0(i U 、)0(i δ带入修正方程式反复迭代,结果与给定的允许误差ε进行判断,若小于ε则迭代结束,进而求出各线路功率,各母线电压、功率,各支路功率。

. ... ..能源学院课程设计课程名称:电力系统分析设计题目:简单环形网络的潮流计算学院:电力学院专业:电气工程及其自动化班级:电气(本)1202班姓名:罗通学号:1210240073成绩:指导教师:莉、彦迪日期:2014年12月8日—2014年12月19日潮流计算是在给定电力系统网络结构、参数和决定系统运行状态的边界条件的情况下确定系统稳态运行状态的一种基本方法,是电力系统规划和运营中不可缺少的一个重要组成部分。
可以说,它是电力系统分析中最基本、最重要的计算,是系统安全、经济分析和实时控制与调度的基础。
常规潮流计算的任务是根据给定的运行条件和网络结构确定整个系统的运行状态,如各母线上的电压(幅值及相角)、网络中的功率分布以及功率损耗等。
潮流计算的结果是电力系统稳定计算和故障分析的基础。
在电力系统运行方式和规划方案的研究中,都需要进行潮流计算以比较运行方式或规划供电方案的可行性、可靠性和经济性。
同时,为了实时监控电力系统的运行状态,也需要进行大量而快速的潮流计算。
因此,潮流计算是电力系统中应用最广泛、最基本和最重要的一种电气运算。
在系统规划设计和安排系统的运行方式时,采用离线潮流计算;在电力系统运行状态的实时监控中,则采用在线潮流计算。
是电力系统研究人员长期研究的一个课题。
它既是对电力系统规划设计和运行方式的合理性、可靠性及经济性进行定量分析的依据,又是电力系统静态和暂态稳定计算的基础。
前言------------------------------------------------------------------------------------------2第一章:简单环形网络的潮流计算原理--------------------------------------41.1 电力线路和变压器上的功率损耗、电压降落及电能损耗--------------- 41.2电压降落、电压损耗、电压偏移及电压调整的概念---------------------- 51.3闭环网的潮流计算步骤---------------------------------------------------------- 6第二章:简单环形网络的潮流计算过程-------------------------------------- 72.1参数整理---------------------------------------------------------------------------- 72.2计算网络参数及等效电路------------------------------------------------------- 82.3电力系统潮流计算的运用------------------------------------------------------- 102.4注意事项---------------------------------------------------------------------------- 10 第三章:P-Q分解法的基本潮流算法-------------------------------------------113.1 P-Q分解法的原理----------------------------------------------------------------113.2 P-Q分解法的特点 ------------------------------------------ 133.3 P-Q分解法的潮流计算步骤 --------------------------------- 14 总结-------------------------------------------------------------------------------------------16辞-------------------------------------------------------------------------------------------17参考文献------------------------------------------------------------------------------------18第一章:简单环形网络的潮流计算原理本章主要容包括:研究简单电力系统正常运行状态下的潮流分布,以及方便潮流计算化简网络的方法。
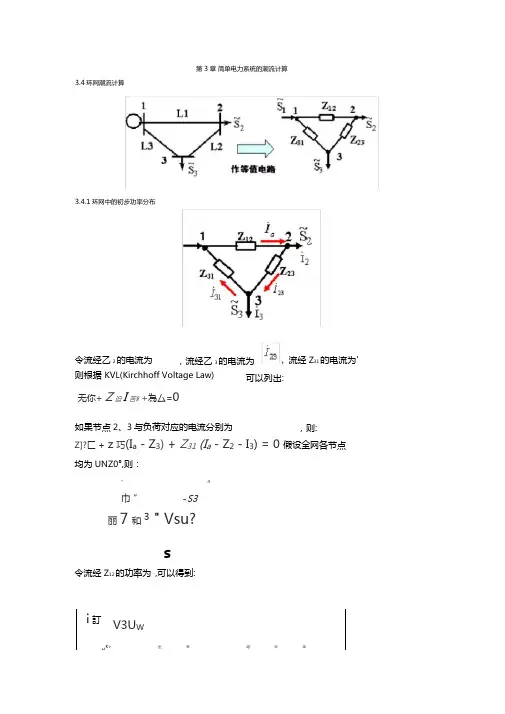
Z]?匚 + z 巧(I a - Z 3) + Z 31 (I a - Z 2 - I 3) = 0 假设全网各节点均为UNZ0°,则:* 4巾 ” -S3丽7和 3 " Vsu?s令流经Z 12的功率为-,可以得到: i 訂 H V3U WK> 出 來 嘟 半 拿3.4环网潮流计算第3章 简单电力系统的潮流计算3.4.1环网中的初步功率分布令流经乙2的电流为 则根据 KVL(Kirchhoff Voltage Law) 流经Z 31的电流为',流经乙3的电流为 可以列出:无你+ Z 迫I 苦§ +為厶=0如果节点2、3与负荷对应的电流分别为 ,则:Z]2S卄 Z石(久一S2~) + Z^S.-S2-S3)二020+i5MVA -2-ilMVA18+14MVAS115+jlOM 17+jllMV4冷 〔厶2 +2石+Z31)同理* S —"彳23十目十z 口S) b (Z^ + 2加+2引)可以理解为用力矩法求梁的反作用力:这两个公式可以推广到2节点、4节点 在求得S 和S bi 后,便可求得环网中各段的功率,即不包括线路功率损耗的功率 分布,这称为环网中的初步功率分布。
g 1 15+jlOMVA 2— 17+订 1MVA如果支路功率由两个方向实际流入一个节点, 则该节点称为功率分点,可以标为AF1 A 1 F218+j4MVA有时有功功率分点和无功功率分点不一致,可以分别表示为A、二3.4.2环网的实际功率分布和电压降落从功率分点将环网解开成两个开式网,然后分别对两个开式网计算功率分布和电压降落。
如果有功功率分点和无功功率分点不一致,则多以无功功率分点解开环网成为两个开式网。
[例3-5]如图系统,U=115kV,头二20 + J13.88A/E4S3 =10 + /9.038A/E4乙2=13.2+j17.16 Q,乙3=9.9+j12.87 Q =N,(1)试求功率分布。

银川能源学院课程设计课程名称:电力系统分析设计题目:简单环形网络的潮流计算学院:电力学院专业:电气工程及其自动化班级:电气(本)1202班*名:**学号:**********成绩:指导教师:李莉、张彦迪日期:2014年12月8日—2014年12月19日潮流计算是在给定电力系统网络结构、参数和决定系统运行状态的边界条件的情况下确定系统稳态运行状态的一种基本方法,是电力系统规划和运营中不可缺少的一个重要组成部分。
可以说,它是电力系统分析中最基本、最重要的计算,是系统安全、经济分析和实时控制与调度的基础。
常规潮流计算的任务是根据给定的运行条件和网络结构确定整个系统的运行状态,如各母线上的电压(幅值及相角)、网络中的功率分布以及功率损耗等。
潮流计算的结果是电力系统稳定计算和故障分析的基础。
在电力系统运行方式和规划方案的研究中,都需要进行潮流计算以比较运行方式或规划供电方案的可行性、可靠性和经济性。
同时,为了实时监控电力系统的运行状态,也需要进行大量而快速的潮流计算。
因此,潮流计算是电力系统中应用最广泛、最基本和最重要的一种电气运算。
在系统规划设计和安排系统的运行方式时,采用离线潮流计算;在电力系统运行状态的实时监控中,则采用在线潮流计算。
是电力系统研究人员长期研究的一个课题。
它既是对电力系统规划设计和运行方式的合理性、可靠性及经济性进行定量分析的依据,又是电力系统静态和暂态稳定计算的基础。
前言------------------------------------------------------------------------------------------2第一章:简单环形网络的潮流计算原理--------------------------------------41.1 电力线路和变压器上的功率损耗、电压降落及电能损耗--------------- 41.2电压降落、电压损耗、电压偏移及电压调整的概念---------------------- 51.3闭环网的潮流计算步骤---------------------------------------------------------- 6第二章:简单环形网络的潮流计算过程-------------------------------------- 72.1参数整理---------------------------------------------------------------------------- 72.2计算网络参数及等效电路------------------------------------------------------- 82.3电力系统潮流计算的运用------------------------------------------------------- 102.4注意事项---------------------------------------------------------------------------- 10 第三章:P-Q分解法的基本潮流算法-------------------------------------------113.1 P-Q分解法的原理----------------------------------------------------------------113.2 P-Q分解法的特点 ------------------------------------------ 133.3 P-Q分解法的潮流计算步骤 --------------------------------- 14 总结-------------------------------------------------------------------------------------------16谢辞-------------------------------------------------------------------------------------------17参考文献------------------------------------------------------------------------------------18第一章:简单环形网络的潮流计算原理本章主要内容包括:研究简单电力系统正常运行状态下的潮流分布,以及方便潮流计算化简网络的方法。
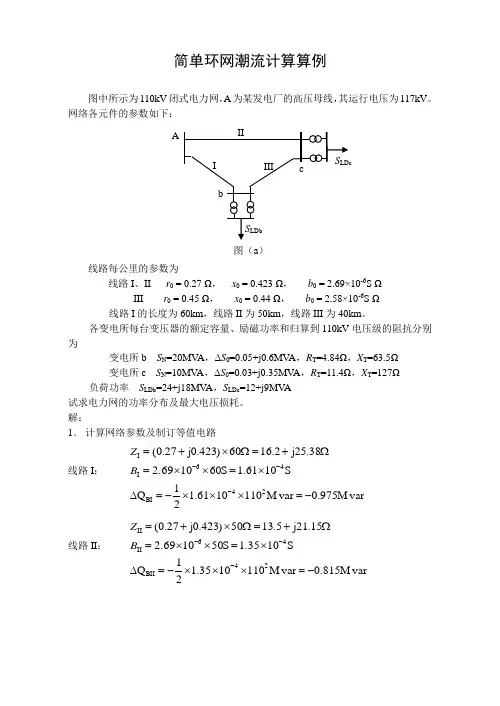
简单环网潮流计算算例图中所示为110kV 闭式电力网,A 为某发电厂的高压母线,其运行电压为117kV 。
网络各元件的参数如下:线路每公里的参数为线路I 、II r 0 = 0.27 Ω, x 0 = 0.423 Ω, b 0 = 2.69×10-6S Ω III r 0 = 0.45 Ω, x 0 = 0.44 Ω, b 0 = 2.58×10-6S Ω线路I 的长度为60km ,线路II 为50km ,线路III 为40km 。
各变电所每台变压器的额定容量、励磁功率和归算到110kV 电压级的阻抗分别为变电所b S N =20MV A ,ΔS 0=0.05+j0.6MV A ,R T =4.84Ω,X T =63.5Ω 变电所c S N =10MV A ,ΔS 0=0.03+j0.35MV A ,R T =11.4Ω,X T =127Ω 负荷功率 S LDb =24+j18MV A ,S LDc =12+j9MV A试求电力网的功率分布及最大电压损耗。
解:1. 计算网络参数及制订等值电路 线路I : var M 975.0var M 1101061.121Q S1061.1S 60102.6938.25j 2.1660)423.0j 27.0(24BI 46I I -=⨯⨯⨯-=∆⨯=⨯⨯=Ω+=Ω⨯+=---B Z 线路II : var M 815.0var M 1101035.121Q S 1035.1S 50102.6915.21j 5.1350)423.0j 27.0(24BII 46II II -=⨯⨯⨯-=∆⨯=⨯⨯=Ω+=Ω⨯+=---B Z图(a )线路III : var M 623.0var M 1101003.121Q S1003.1S 40102.587.61j 1840)44.0j 45.0(24BIII 46III III -=⨯⨯⨯-=∆⨯=⨯⨯=Ω+=Ω⨯+=---B Z变电所b : j1.2MV A 1.0j0.6)MV A 05.0(2 1.753j 42.240)3.56j 84.4(21ob Tb +=+⨯=∆Ω+=Ω⨯+=S Z 变电所c :j0.7MV A 06.0j0.35)MV A 03.0(2 3.56j 7.540)271j 4.11(21oc Tc +=+⨯=∆Ω+=Ω⨯+=S Z 等值电路示于图(b )中2. 计算节点b 和c 的运算负荷 .36MV A 2j 0.18MV A )75.31j 42.2(1101824222Tb +=++=∆S j19.96MVA28.24j0.623MVA -j0.975-j1.20.1j2.360.18j1824j j BIIBI ob Tb LDb b +=+++++=∆+∆+∆+∆+=Q Q S S S Sj1.18MV A 0.106MV A )5j63.7.5(110912222Tc +=++=∆S j9.44MVA17.12j0.815MVA -j0.623-j0.70.06j1.180.106j912j j BIIBIII oc Tc LDc c +=+++++=∆+∆+∆+∆+=Q Q S S S S3. 计算闭式网络中的功率分布A A 2bc BI BII 图(b )j15.79MVA18.64MVA 64.13-47.7j j21.15)5.13)(j9.4417.12()j38.755.31)(j19.9628.24()(IIIII I IIc III II b I +=-++-+=++++=******Z Z Z Z S Z Z S S j13.6MVA8.71MVA 64.13-47.7j j42.98)2.34)(j9.4417.12()j25.382.16)(j19.9628.24()(IIIII I III I c I b II +=-++-+=++++=******Z Z Z Z Z S Z S S验算:j29.4MVA 36.45j9.44MVA 17.21j19.9628.24j29.39MVA36.44j13.6MVA 17.8j15.7964.18c b II I +=+++=++=+++=+S S S S 可见,计算结果误差很小,无需重算。

第三章 电力系统的潮流计算3-1 电力系统潮流计算就是对给定的系统运行条件确定系统的运行状态。
系统运行条件是指发电机组发出的有功功率和无功功率(或极端电压),负荷的有 功功率和无功功率等。
运行状态是指系统中所有母线(或称节点)电压的幅值和 相位,所有线路的功率分布和功率损耗等。
3-2 电压降落是指元件首末端两点电压的相量差。
电压损耗是两点间电压绝对值之差。
当两点电压之间的相角差不大时, 可以近似地认为电压损耗等于电压降落的纵分量。
电压偏移是指网络中某点的实际电压同网络该处的额定电压之差。
电压 偏移可以用kV 表示,也可以用额定电压的百分数表示。
电压偏移=%100⨯-NNV V V 功率损耗包括电流通过元件的电阻和等值电抗时产生的功率损耗和电压 施加于元件的对地等值导纳时产生的损耗。
输电效率是是线路末端输出的有功功率2P 与线路首端输入的有功功率1P 之比。
输电效率=%10012⨯P P 3-3 网络元件的电压降落可以表示为()•••••+=+=-2221V V I jX R V V δ∆式中,•2V ∆和•2V δ分别称为电压降落的纵分量和横分量。
从电压降落的公式可见,不论从元件的哪一端计算,电压降落的纵、横分量计算公式的结构都是一样的,元件两端的电压幅值差主要有电压降落的纵分量决定,电压的相角差则由横分量决定。
在高压输电线路中,电抗要远远大于电阻,即R X 〉〉,作为极端的情况,令0=R ,便得V QX V /=∆,V PX V /=δ上式说明,在纯电抗元件中,电压降落的纵分量是因传送无功功率而产生的,而电压降落的横分量则是因为传送有功功率产生的。
换句话说,元件两端存在电压幅值差是传送无功功率的条件,存在电压相角差则是传送有功功率的条件。
3-4 求解已知首端电压和末端功率潮流计算问题的思路是,将该问题转化成已知同侧电压和功率的潮流计算问题。
首先假设所有未知点的节点电压均为额定电压,从线路末端开始,按照已知末端电压和末端潮流计算的方法,逐段向前计算功率损耗和功率分布,直至线路首端。
3.3简单闭式网络的电压和功率分布计算闭式网络:电网中任意负荷都只能从两个方向供电,包括双端供电网和多级电压环网。
3.3.1 双端供电网潮流计算 (1)初步潮流计算根据基尔霍夫电压、电流定律:()()()()()()1122331223233112312311231123123A B a b a b A Ba b A Ba b U U Z I Z I Z I I I I I I I Z Z I Z I U U I Z Z Z Z Z Z Z I Z Z I U U I I I I Z Z Z Z Z Z ⎧=++-⎪=+⎨⎪=-⎩⎧++-=+⎪++++⎪⇒⎨++-⎪=+-=-⎪++++⎩根据*S U I = ,将上式各量取共轭值,令0N NU U =∠ ,全式乘以N U ,可得其中1LD S 和3LD S —供载功率,LS —循环功率。
获得电源输出功率1S 和3S 后,进而可以求出各段线路上的传输功率,从而可以判断各段线路上传输功率的实际方向(确定功率分点——实际的双端供电点,分为有功功率分点、无功功率分点)。
(2)最终潮流计算初步潮流计算后,在功率分点将网络打开,分为两个开式电网(当有功功率分点和无功功率分点不一致时,常选电压较低的分点将电网打开。
鉴于高压电网中,电压损耗主要由无功功率流动所致,无功功率分点电压往往低于有功功率分点电压,故一般选取无功功率分点将电网打开)。
开式电网潮流计算:已知终端电压和始端电压,采用迭代法计算。
几点说明:(1) 环网(A BU U = )——无循环功率。
(2) 35KV 及以下电网,可以忽略线路功率损耗,因此初步潮流分布就是最终潮流分布。
(3) 均一电网(C i i X R =常数),供载功率为在均一网中,有功功率和无功功率的分布彼此独立,且可以只利用各线段的电阻(或电抗)分别计算。
对于电压等级和导线截面相同的均一网,有功功率和无功功率的分布仅由线路长度决定。
简单配电网的潮流计算电力系统正常运行状况下,运行、管理和调度人员需要知道在给定运行方式下各母线的电压是否满意要求,系统中的功率分布是否合理,元件是否过载,系统有功、无功损耗各是多少等等状况。
为了了解这些运行状况就需要进行潮流计算。
潮流计算:依据已知的负荷(功率)及电源电压计算出其它节点的电压和元件上的功率分布。
潮流计算是电力系统中最基本、最常用的一种汁算。
开式网:只有一端电源供电的网络。
一.计算中的两种类型:1.同一电压等级的开式网计算 2.不同电压等组的开式网计算二.计算中的三种状况:1.已知末端电压和功率,求首端电压和功率采纳将电压和功率由已知点向未知点逐段递推计算的方法。
即已知和,求和,见图1。
图1 已知末端电压和功率,求首端电压和功率(1)功率计算:2)电压计算:(3)对功率和电压交替计算,求和对于110kV及以下的网络,在计算电压损耗时常略去横重量,使计算进一步简化。
在计算时需留意变压器两侧参数与电压的归算。
2.已知首端电压和功率,求末端电压和功率即已知和,求和,这种状况的电路见图2。
图2 已知首端电压和功率,求末端电压和功率(1)功率计算:2.电压计算:(3)对功率和电压交替计算:求和3.已知末端功率和首端电压,求首端功率和末端电压(常见)即已知和,求末端和首端,这种状况的电路见图3。
图 3 已知末端功率和首端电压,求首端功率和末端电压近似计算(常用):精确计算:不断迭代!(1)设定各节点电压等于其额定电压:(2)与第一种状况一样求出功率分布:(3)与其次种状况一样求出各节点电压分布:常见的状况是给出开式配电网的末端负荷与首端电压。
对于这种状况可进一步简化计算,不必进行反复递推。
设全网为额定电压(一般可将全网参数归算到同一个电压等级),由网络末端向首端推算各元件的功率损耗和功率分布,而不计算电压;待求得首端功率后,再由给定的首端电压与求得的首端功率、网络各处的功率分布,从首端向末端推算各元件电压损耗和各母线(节点)电压,此时不再重新计算功率损耗与功率分布。
简单环形网络的潮流计算银川能源学院课程设计课程名称:电力系统分析设计题目:简单环形网络的潮流计算学院:电力学院专业:电气工程及其自动化班级:电气(本)1202班姓名:罗通第一章:简单环形网络的潮流计算原理本章主要内容包括:研究简单电力系统正常运行状态下的潮流分布,以及方便潮流计算化简网络的方法。
电力系统的潮流分布是描述电力系统运行状态的技术术语,它表明电力系统在某一确定的运行方式和接线方式下,系统中从电源经网络到负荷各处的电压、电流、功率的大小和方向的分布情况。
电力系统的潮流分布,主要取决于负荷的分布、电力网参数以及和供电电源间的关系。
对电力系统在各种运行方式下进行潮流分布计算,以便确定合理的供电方案,合理的调整负荷。
通过潮流分布计算,还可以发现系统中薄弱环节,检查设备、元件是否过负荷,各节点电压是否符合要求,以便提出必要的改进措施,实施相应的调压措施,保证电力系统的电能质量,并使整个电力系统获得最大的经济性。
1.1 电力线路和变压器上的功率损耗、电压降落及电能损耗计算电力线路和变压器上的功率损耗、电压降落常用的公式总结如下:功率损耗:线路和变压器阻抗支路 X U Q P j R U Q P S Z 222222+++=∆•(1-1)线路的对地支路 212112121U jB U G S Y -=∆•变压器的励磁支路22U jB U G S T T YT +=∆•(1-2)电压降落:⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+=∆+∆=•U QR PX U U QX PR U U j U U d δδ(1-3)始端电压:⎪⎪⎩⎪⎪⎨⎧∆+=+∆+=∠=+∆+=-••U U Utg U U U U U U j U U 2122212221)()(U )0()(U δδδδ 设(1-4 )注意:采用以上公式计算时,P 、Q 、U 一定要用同一点(同一侧)的值。
电力线路的电能损耗:折线代曲线法:k nk k k k t R U Q P dt t P W ⋅⎪⎪⎭⎫ ⎝⎛+=∆=∆⎰∑=87601222)(最大功率损耗时间法:max max τP W ∆=∆(根据负荷性质ϕcos 查出max T ,由max cos T ϕ查max maxτ-T 曲线得max τ)经验法:max 8760P F W ∆⋅⋅=∆(F 为年负荷损耗率,2)1(f K f K F ⋅-+⋅=,f 为年负荷率,8760maxT f =,K=0.1~0.4经验数据) 变压器的电能损耗:max 20100087601000τ⎪⎪⎭⎫⎝⎛+=∆+∆=∆NK ZT YT T S SP P W W W推广到n 台:max 20100087601000τ⎪⎪⎭⎫⎝⎛+=∆N k T nS SP n P nW 1.2电压降落、电压损耗、电压偏移及电压调整的概念(1) 电压降落——是指线路始末两端电压的相量差⎪⎭⎫⎝⎛-••21U U 。
(2) 电压损耗——是指线路始末两端电压的数值差()21U U -。
电压损耗%100(%)21⨯-=NU U U (3) 电压偏移——是指线路始端或末端电压与线路额定电压的数值差。
如线路始端偏移为()N U U -1,线路末端电压偏移为()N U U -2。
若以百分值表示,即有: 始端电压偏移%100(%)1⨯-=N NU U U 末端电压偏移%100(%)2⨯-=NNU U U(4) 电压调整——是指线路末端空载电压20U 与负载电压2U 的数值差()220U U -。
电压调整%100(%)20220⨯-=U U U1.3闭环网的潮流计算步骤(1) 把闭环网简化成两端供电网。
(2) 以N U 为全网电压(即不计电压损耗),求出两端的注入功率a S •,b S •,进而求出各支路的流动功率(不计网络中功率损耗)。
两端电压相等时:•∑•••∑=Z Z S S mm a两端电压不相等时:••∑•••+∑=c mm aS Z Z S S对均一网: ∑••∑=l l S S mm a经济功率分布: ∑•-•∑=R R S S mm o a (3) 找出功率分点,从功率分点把闭环网变成两个辐射网。
(4) 从功率分点开始,分别对两个辐射网逐段推算电压损耗、功率损耗,用到公式(1-1)、(1-2)、(1-3)、(1-4),从而进行潮流分布计算。
(5) 还原成实际网的潮流分布。
在还原过程中,功率满足0=∑•S ,计算分功率时,用到公式:••∑•∑••∑•••+=mmm m Z Z S U Z E E S 1第二章:简单环形网络的潮流计算过程2.1参数整理如图所示为110kV 闭式电力网,A 为某发电厂的高压母线,UA=117kV ,网络各元件参数如下:线路I :Z I =(6.2+j25.38),B I =1.61×10-4S线路II:Z II =(13.5+j21.15),B II =1.35×10-4S 线路III:Z III =(18+j17.6),B III =1.61×10-4S各变电所每台变压器的额度容量、励磁功率和归算110KV 电压等级的阻抗如下:变电所B :Ω+=+=∆=)5.6384.4(,)6.005.0(~,200j Z MVA j S MVA S TB N变电所C:Ω+=+=∆=)1274.11(,)35.003.0(~,100j Z MVA j S MVA S TC N负荷功率:MVA j S MVA j S LD B LD B )912(~,)1824(~+=+=a)分析计算该网络的功率分布及最大电压损耗。
I Z A BIIIZ Z A BIQ ∆j BS CS BIII(b)~IZ BIQ ∆j I S IIIS CS BIIQ ∆j 2A(c)图2-1 例2-1的简单闭式电力网2.2计算网络参数及等效电路(1) 计算网络参数并制定等效电路线路I II 和III 的阻抗和电纳已知,它们的充电功率分别为var 25.1var 1101003.12var 63.1var 1101035.12var 95.1var 1101061.12243242241M M Q M M Q M M Q B B B -=⨯⨯-=∆-=⨯⨯-=∆-=⨯⨯-=∆---I每个变电所内均有两台变压器并联运行,所以变电所B MVA j MVA j S j j Z OBTB )2.11.0()6.005.0(2~)75.3142.2()5.6384.4(21+=+=∆Ω+=Ω+=变电所C MVA j MVA j S j j Z OCTC )7.006.0()35.003.0(2~)5.637.5()1274.11(21+=+=∆Ω+=Ω+=等效电路如图2-1b 所示 (2)计算节点B 和C 的运算负荷MVA j MVA j j j j j Q j Q j S S S S MVA j MVA j S MVAj MVA j j j j j Q j Q j S S S S MVA j MVA j S B B OC TC LDB C TC B B OB TB LDB B TB )44.917.12()815.0625.07.006.018.1106.0912(~~~~)18.1106.0()5.637.5(110912~)96.1928.24()625.0975.02.11.036.218.01824(~~~~)36.218.0()75.3142.2(1101824~3222221222+=--+++++=∆+∆+∆+∆+=+=++=∆+=--+++++=∆+∆+∆+∆+=+=++=∆(3) 计算闭式网络中的功率分MVAj j j j j j Z Z Z Z S Z Z S S C B 13.647.47)15.215.13)(44.917.12(13.647.47)75.385.31)(96.1928.24(~)(~~3*212321--++--+=++++=*****(4) 计算电压损耗由于线路I 和线路II 的功率均流向节点B ,故节点B 为功率分点,这点的电压最低。
为了计算线路I 的电压损耗,要用A 点的电压和功率1~A S .kVkVU X Q R P U MVA j j j S S S A A A L A 39.611738.2505.172.1645.19)05.1745.19()38.252.16(1108.1565.188.1565.18~~~11111222111=⨯+⨯=+=∆+=⎥⎦⎤⎢⎣⎡++++=∆+=变电所B 高压母线的实际电压为kV kV U U U A 61.110)39.6117(1=-=∆-=2.3电力系统潮流计算的运用(1)检查电力系统各元件是否负荷。
(2)为电力系统的规划和扩建提供依据。
(3)检查电力系统各节点的电压是否满足电压质量的要求。
2.4注意事项计算时,需注意如下两个问题。
(1) 若已知电源端电压,而非功率分点电压,应按什么电压起算?可设网络中各点电压均为U ,先算功率损耗,求得电源功率后,再往后推算电压降落。
(2) 若有功功率分点与无功功率分点不一致,怎么办?一般以无功功率分点为计算起点。
第三章:P-Q分解法的基本潮流算法3.1 P-Q分解法的原理采用极坐标形式表示节点电压,能够根据电力系统实际运行状态的物理特点,对牛顿潮流计算的数学模型进行合理的简化。
在交流高压电网中,输电线路的电抗要比电阻大得多,系统中母线有功功率的变化则主要受母线电压幅值变化的影响。
在修正方程式的系数矩阵中,偏导数PV∂∆∂和P∆∂∂δ数值是相当小的。
作为简化的第一步,可以将方程式(3-1)中的子块N和K略去不计,即认为它们的元素为零。
这样,n-1+m阶的方程式(3-1)便分解为一个n-1阶和一个m阶的方程ΔP = - HΔδ(3-2)ΔQ= - LV D-1ΔV(3-3)这一简化大大地节省了机器内存和解题时间。
方程式(3-2)和(3-3)表明,节点的有功功率不平衡量只用于修正电压的相位,节点的无功功率不平衡量只用于修正电压的幅值。
这两组方程轮流迭代,这就是所谓的有功-无功功率分解法。
但是矩阵H和L的元素都是节点电压幅值和相角差的函数,其数值在迭代过程中是不断变化的。
因此,最关键的一步简化就在于,把系数矩阵H和L简化为常数矩阵。
它的根据是什么呢?在一般情况下,线路两端电压的相角差是不大的(不超过10o~20o),因此可以认为cosδij≈1, G ij sinδij<<B ij此外,与系统各节点无功功率相适应的导纳BLDi必远小于该节点自导纳的虚部,即BLDi=Qi/V i2﹤﹤B ii和Qi﹤﹤V i2B ii考虑到以上的关系,矩阵H 和L 的元素的表达式便简化成H ij =V i V j B ij (i ,j=1,2, …,n-1) (3-4)L ij =V i V j B ij (i ,j=1,2, …,m ) (3-5)而系数矩阵H 和L 则可以分别写成⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦1111112211,n-1n-12211222222,n-1n-1n-1n-1,11n-1n-12n-1n-1,n-1n-1V B V V B V V B V V B V V B V V B V H =V B V V B V V B V 11121,n-11121222,n-122n-1n-1n-1,1n-1,2n-1,n-1B B L B V V B B L B VVV V B B L B ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦=?'D1D1V B V = (3-6)1111112211,2211222222,,112,11121,1121222,22,1,2,m m m m m m m m m m m m m m m m m m m m D2D2V B V V B V V B V V B V V B V V B V L V B V V B V V B V B B B V V B B B V V V V B B B V B V ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⨯⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦''= (3-7)将(3-6)和(3-7)分别代入(3-2)和(3-3),便得到ΔP = -V D1 B ’V D1ΔδΔQ= -V D2 B ”ΔV用 V D1-1和V D2-1分别左乘以上两式便得V D 1-1ΔP= - B ’V D 1Δδ (3-8) V D 2-1ΔQ= - B ”ΔV (3-9)这就是简化了的修正方程式,它们也可展开写成1111121,n-111221222,n-1222n-1n-1n-1,1n-1,2n-1,n-1n-1n-1P V B B B V P B B B V V V B B B P V δδδ⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ΔΔΔΔ=-ΔΔ (3-10)1111121m 1221222m 22m m1m2mm m m Q V B B B V Q B B B V V V B B B Q V ⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦ΔΔΔΔ=-ΔΔ (3-11) 在这两个修正方程式中,系数矩阵都由节点导纳矩阵的虚部构成,只是阶次不同,矩阵B /为n-1阶,不含平衡节点对应的行和列,矩阵B //为m 阶,不含平衡节点和PV 节点对应的行和列。