习题9电磁感应与电磁场
- 格式:doc
- 大小:408.00 KB
- 文档页数:8

电磁场练习题电磁场是物理学中重要的概念,广泛应用于电力工程、通信技术等领域。
为了更好地理解和掌握电磁场的相关知识,以下是一些练习题,帮助读者巩固对电磁场的理解。
练习题1:电场1. 有一电荷+Q1位于坐标原点,另有一电荷+Q2位于坐标(2a, 0, 0)处。
求整个空间内的电势分布。
2. 两个无限大平行带电板,分别带有电荷密度+σ和-σ。
求两个带电板之间的电场强度。
3. 一个圆环上均匀分布有总电荷+Q,圆环的半径为R。
求圆环轴线上离圆环中心距离为x处的电场强度。
练习题2:磁场1. 一个无限长直导线通过点A,导线中电流方向由点A指向B。
求点A处的磁场强度。
2. 一个长直导线以λ的线密度均匀分布电流。
求距离导线距离为r处的磁场强度。
3. 一半径为R、载有电流I的螺线管,求其轴线上离螺线管中心的距离为x处的磁场强度。
练习题3:电磁场的相互作用1. 在一均匀磁场中,一电子从初始速度为v0的方向垂直进入磁场。
求电子做曲线运动的轨迹。
2. 有两个无限长平行导线,分别通过电流I1和I2。
求两个导线之间的相互作用力。
3. 一个电荷为q的粒子以速度v从初始位置x0进入一个电场和磁场同时存在的区域。
求电荷受到的合力。
练习题4:电磁场的应用1. 描述电磁波的基本特性。
2. 电磁感应现象的原理是什么?列举几个常见的电磁感应现象。
3. 解释电磁场与电路中感应电动势和自感现象的关系。
根据上述练习题,我们可以更好地理解和掌握电磁场的基本原理和应用。
通过解答这些练习题,我们能够加深对电场、磁场以及电磁场相互作用的理解,并掌握其在实际应用中的运用。
希望读者能够认真思考每道练习题,尽量自行解答。
如果遇到困难,可以参考电磁场相关的教材、课件等资料,或者向老师、同学寻求帮助。
通过不断练习和思考,相信读者可以彻底掌握电磁场的相关知识,为今后的学习和应用奠定坚实的基础。

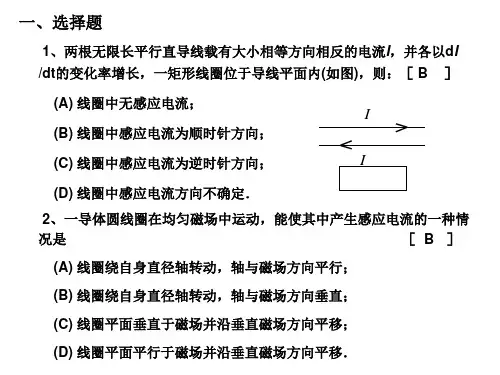
9-1两个半径分别为R 和r 的同轴圆形线圈相距x ,且R >>r ,x >>R .若大线圈通有电流I 而小线圈沿x 轴方向以速率v 运动,试求小线圈回路中产生的感应电动势的大小. 解:在轴线上的磁场()()22003322222IR IR B x R x R xμμ=≈>>+32202xr IR BS πμφ==v xr IR dt dx x r IR dt d 422042202332πμπμφε=--=-=9-2如图所示,有一弯成θ 角的金属架COD 放在磁场中,磁感强度B ϖ的方向垂直于金属架COD 所在平面.一导体杆MN 垂直于OD 边,并在金属架上以恒定速度v ϖ向右滑动,v ϖ与MN 垂直.设t =0时,x = 0.求当磁场分布均匀,且B ϖ不随时间改变,框架内的感应电动势i ε.解:12m B S B xy Φ=⋅=⋅,θtg x y ⋅=,vt x =22212/()/i d dt d Bv t tg dt Bv t tg εϕθθ=-=-=⋅,电动势方向:由M 指向N9-3 真空中,一无限长直导线,通有电流I ,一个与之共面的直角三角形线圈ABC 放置在此长直导线右侧。
已知AC 边长为b ,且与长直导线平行,BC 边长为a ,如图所示。
若线圈以垂直于导线方向的速度v 向右平移,当B 点与直导线的距离为d 时,求线圈ABC 内的感应电动势的大小和方向。
解:当线圈ABC 向右平移时,AB 和AC 边中会产生动生电动势。
当C 点与长直导线的距离为d 时,AC 边所在位置磁感应强度大小为:02()IB a d μπ=+AC 中产生的动生电动势大小为:xr IRx vC DOxMθBϖv ϖ02()AC AC IbvBl v a d μεπ==+,方向沿CA 方向如图所示,在AB 边上取微分元dl ,微分元dl 中的动生电动势为,()AB d v B dl ε=⨯⋅v v v其方向沿BA 方向。

电磁场与电磁感应的关系电磁场和电磁感应是电磁学的两个重要概念,它们之间存在紧密的关系。
电磁场是指由电荷或电流所产生的物理场,而电磁感应则是指当一个导体磁通量发生变化时,在导体中会产生感应电动势。
本文将详细探讨电磁场和电磁感应之间的关系,并介绍它们在现实生活和科技应用中的重要性。
一、电磁场的基本原理电荷和电流都是产生电磁场的重要因素。
根据库仑定律,电荷之间的相互作用力与它们之间的距离成平方反比。
这意味着电荷会在周围形成一个电场,电场中的电荷会受到电场力的作用。
同样地,电流也会产生磁场,磁场中的磁感应强度会影响磁场中的电流。
二、电磁感应的原理电磁感应是指当导体中的磁通量发生变化时,在导体中会产生感应电动势。
磁通量是磁场线穿过某个面积的数量,用符号Φ表示。
根据法拉第电磁感应定律,当磁通量Φ发生变化时,感应电动势E的大小与磁通量的变化率成正比。
三、电磁场与电磁感应的关系电磁场和电磁感应之间存在着紧密的关系。
首先,电磁场的存在是电磁感应的基础。
只有当存在磁场时,导体才会感应出电动势。
其次,电磁感应也会产生磁场。
根据安培环路定律,当导体中有电流通过时,会形成闭合的磁场线。
这个磁场又会影响到其他导体中的电流。
在实际应用中,电磁感应的原理被广泛应用于发电机、变压器等设备中。
发电机通过旋转的磁场线穿过线圈,感应出电动势,从而转化为电能。
变压器利用电磁感应的原理来调整电压的大小。
另外,电磁场和电磁感应也在电磁波的传播中起着重要作用。
电磁波是一种由振荡的电场和磁场组成的波动现象,广泛应用于通信、无线电等领域。
总结起来,电磁场和电磁感应是相辅相成的概念。
电磁场的存在为电磁感应提供了基础,而电磁感应又反过来影响着电磁场的分布。
它们之间的关系不仅仅是理论上的联系,更在现实生活和科技应用中发挥着重要作用。
理解和掌握电磁场与电磁感应的关系,对于深入理解电磁学的原理和应用具有重要意义。


一。
选择题[ D ]1.(基础训练3)在一自感线圈中通过的电流I 随时间t 的变化规律如图(a)所示,若以I 的正流向作为 的正方向,则代表线圈内自感电动势 随时间t 变化规律的曲线应为图(b)中(A)、(B)、(C)、(D)中的哪一个? 【分析】dt dI LL -=ε,在每一段都是常量。
dtdI[ D ]2. (基础训练5)在圆柱形空间内有一磁感强度为B的均匀磁场,如图所示.B的大小以速率d B /d t 变化.在磁场中有A 、B 两点,其间可放直导线AB 和弯曲的导线AB ,则 (A) 电动势只在导线AB 中产生. (B) 电动势只在AB 导线中产生. (C) 电动势在AB 和AB 中都产生,且两者大小相等.(D) AB 导线中的电动势小于导线中的电动势 【分析】连接oa 与ob ,ob ab ob oab εεεε++=。
因为涡旋电场总是与圆柱截面垂直,所以oa 和ob 上的涡旋电场方向处处垂直于oa 、ob ,即0=⋅==⎰→→l d E ob ob εεoab ob d dB S dt dtφεε==-=- o ab oabd d dtdtϕϕ∴<[ B ]3.(基础训练6)如图12-16所示,直角三角形金属框架abc 放在均匀磁场中,磁场B平行于ab 边,bc 的长度为l .当金属框架绕ab 边以匀角速度ω转动时,abc 回路中的感应电动势和a 、c 两点间的电势差U a – U c 为(A) 0ε= 221l B U U c a ω=- (B) 0ε= 221l B U U c a ω-=-(C)2B l εω=221l B U U c a ω=- (D) 2B l εω= 221l B U U c a ω-=-【分析】ab 边以匀速转动时 0=-=dtd abc φε 22l B l d B v U U U U L c b c a ω-=∙⎪⎭⎫⎝⎛⨯=-=-⎰→→→ t t tt t (b)(a)Bab clω图12-16[ B ]4.(自测提高2)真空中一根无限长直细导线上通电流I ,则距导线垂直距离为a 的空间某点处的磁能密度为(A) 200)2(21a I πμμ (B) 200)2(21a I πμμ (C) 20)2(21I a μπ (D) 200)2(21aI μμ【分析】距离为a 的空间该点的磁感应强度大小为:aIB πμ20=磁能密度为 200022212⎪⎭⎫ ⎝⎛==a I B w m πμμμ [ B ]5.(自测提高5)用导线围成的回路(两个以O 点为心半径不同的同心圆,在一处用导线沿半径方向相连),放在轴线通过O 点的圆柱形均匀磁场中,回路平面垂直于柱轴,如图12-26所示.如磁场方向垂直图面向里,其大小随时间减小,则(A)→(D)各图中哪个图上正确表示了感应电流的流向? 【分析】根据公式S dt B d l E S Ld d ⋅-=⋅⎰⎰⎰感,因为0<dtB d 且磁场方向垂直图面向里,所以感应电流为顺时针方向,再由于感应电流是涡电流,故选B 图。

高三物理练习题:电磁场与电磁感应一、选择题1. 以下哪个量可以描述电磁场线的方向?A. 电位差B. 电流强度C. 磁感应强度D. 电容量2. 在电磁振荡过程中,电磁场的能量主要以什么形式传递?A. 电子动能B. 磁场能量C. 电场能量D. 力学能量3. 假设在一个导体回路中,磁感应强度的变化速率为1 T/s,回路的面积为0.5 m²。
根据法拉第电磁感应定律,通过回路的感应电动势大小为多少?A. 0.5 VB. 0.25 VC. 2 VD. 1 V4. 两根平行长导线,通电方向相反,电流强度分别为 I 和 2I。
若两导线间距离为 d,根据安培力定律,两导线之间的力大小为多少?A. μ₀I²/dB. 2μ₀I²/dC. 3μ₀I²/dD. 4μ₀I²/d5. 若将一个长直导线中通以交变电流,导线周围将会形成一个:A. 强磁场B. 弱磁场C. 强电场D. 弱电场二、计算题1. 一个电磁铁的匝数为 1000,电流强度为 5A,导体的长度为 0.5m。
求这根导线中的磁感应强度大小。
2. 在一个磁感应强度为 0.3T 的电磁场中,一段长度为 0.2m 的导线的感应电动势为 5V。
求导线在电磁场中的速度大小。
三、应用题1. 一辆汽车在磁感应强度为 0.4T 的磁场中运行,汽车的轨道形状是一个圆形,半径为 100m。
若汽车以 30 m/s的速度通过磁场,求汽车所受的磁场力大小。
2. 在一个电磁场中,某导体棒以 20 m/s 的速度向右运动,导体棒的长度为 0.1m。
磁感应强度为 0.5T,导体棒的电阻为2Ω。
求导体棒在电磁场中消耗的功率大小。
四、解答题1. 简述什么是电磁感应现象,并举例说明。
2. 电流通过一个圆形线圈产生的磁场会对其自身产生什么影响?并解释其原因。
注意:以上所有题目均为高三物理相关的练习题,旨在拓展学生对电磁场与电磁感应的理解。
请同学们务必认真思考,并结合所学的知识解答。



第9章 《电磁感应 电磁场理论》复习思考题一、填空题:1.飞机以1s m 200-⋅=v 的速度水平飞行,机翼两端相距离m 30=l ,两端这间可当作连续导体。
已知飞机所在处地磁场的磁感应强度B 在竖直方向上的分量T 1025-⨯。
机翼两端电势差U 为0.12V 。
2.当穿过一个闭合导体回路所包围的面积内的 磁通量 发生变化时,在导体回路中就会产生电流,这种现象称为电磁感应现象。
3.用导线制造成一半径为m 10.0=r 的闭合圆形线圈,其电阻Ω=10R ,均匀磁场B 垂直于线圈平面。
欲使电路有一稳定的感应电流A 01.0=I ,B 的变化率应为__3.18T/s_____________。
4.楞次定律:感生电流的磁场所产生的磁通量总是 阻碍引起感应电流的磁通量的变化。
5.如果导体不是闭合的,即使导体在磁场里做切割磁力线运动也不会产生感应电流,但在导体的两端产生_感应电动势____。
6.楞次定律是 能量守恒和转换 _定律在电磁现象领域中的表现。
二、单选题1.感生电场是 。
(A )由电荷激发,是无源场; (B )由电荷激发,是有源场;(C )由变化的磁场激发,是无源场; (D )由变化的磁场激发,是有源场。
2.关于感应电动势的正确说法是: 。
(A )导体回路中的感应电动势的大小与穿过回路的磁感应通量成正比;(B )当导体回路所构成的平面与磁场垂直时,平移导体回路不会产生感应电动势;(C )只要导体回路所在处的磁场发生变化,回路中一定产生感应电动势;(D )将导体回路改为绝缘体环,通过环的磁通量发生变化时,环中有可能产生感应电动势。
3.交流发电机是根据 原理制成的。
(A )电磁感应; B )通电线圈在磁场中受力转动;(C )奥斯特实验; (D )磁极之间的相互作用。
4.将形状完全相同的铜环和木环静止放置,并使通过两环面的磁通量随时间的变化率相等,则不计自感时, 。
(A )铜环中有感应电动势,木环中无感应电动势(B )铜环中感应电动势大,木环中感应电动势小(C )铜环中感应电动势小,木环中感应电动势大(D )两环中感应电动势相等。

第9章 电稳感应和电磁场 习题及答案1. 通过某回路的磁场与线圈平面垂直指向纸面内,磁通量按以下关系变化:23(65)10t t Wb -Φ=++⨯。
求2t s =时,回路中感应电动势的大小和方向。
解:310)62(-⨯+-=Φ-=t dtd ε当s t 2=时,V 01.0-=ε由楞次定律知,感应电动势方向为逆时针方向2. 长度为l 的金属杆ab 以速率υ在导电轨道abcd 上平行移动。
已知导轨处于均匀磁场B中,B 的方向与回路的法线成60°角,如图所示,B 的大小为B =kt (k 为正常数)。
设0=t 时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向。
解:任意时刻通过通过回路面积的磁通量为202160cos t kl t Bl S d B m υυ==⋅=Φ导线回路中感应电动势为 t kl tmυε-=Φ-=d d 方向沿abcda 方向。
3. 如图所示,一边长为a ,总电阻为R 的正方形导体框固定于一空间非均匀磁场中,磁场方向垂直于纸面向外,其大小沿x 方向变化,且)1(x k B +=,0>k 。
求: (1)穿过正方形线框的磁通量;(2)当k 随时间t 按t k t k 0)(=(0k 为正值常量)变化时,线框中感生电流的大小和方向。
解:(1)通过正方形线框的磁通量为⎰⎰=⋅=Φa S Badx S d B 0 ⎰+=a dx x ak 0)1()211(2a k a +=(2)当t k k 0=时,通过正方形线框的磁通量为)211(02a t k a +=Φ 正方形线框中感应电动势的大小为dt d Φ=ε)211(02a k a += 正方形线框线框中电流大小为)211(02a R k a R I +==ε,方向:顺时针方向4.如图所示,一矩形线圈与载有电流t I I ωcos 0=长直导线共面。
设线圈的长为b ,宽为a ;0=t 时,线圈的AD 边与长直导线重合;线圈以匀速度υ垂直离开导线。
八年级物理练习题:电磁感应电磁感应练习题
题目一:
1. 一根导线被连接到一个电池的两个端口上,并放在一块磁铁附近。
当电流通过导线时,磁铁受到吸引。
请说明这是如何发生的?
题目二:
2. 一个长直导线垂直放置在一块保持不变的磁场中。
如果导线中的电流方向与磁场方向相同,导线将受到一个向上的力。
如果电流方向与磁场方向相反,导线将受到一个向下的力。
请解释这个现象。
题目三:
3. 当电磁感应发生时,电流是如何产生的?请解释法拉第电磁感应定律。
题目四:
4. 简述发电机的工作原理。
说明在发电机中如何利用电磁感应产生电流。
题目五:
5. 请解释电磁感应在变压器中的应用。
说明变压器如何将电能从一个线圈传输到另一个线圈。
题目六:
6. 电磁感应可用于许多设备和技术中。
请举例并解释其中一个实际应用。
题目七:
7. 描述电磁感应实验的步骤。
设计并实施一个简单的电磁感应实验。
题目八:
8. 某个发电站的输出电压为220V。
计算电磁感应原理下,需要多少匝才能将
输出电压增加到440V?
题目九:
9. 当一个磁场变化时,经过具有多个匝数的线圈时,电压的大小会受到影响。
请说明匝数如何影响电磁感应中的电压大小。
题目十:
10. 电磁感应也被应用于感应炉。
解释感应炉是如何利用电磁感应加热金属的。
电磁感应与电磁场理论电磁感应是电磁学中的一个重要概念,它描述了导体中自由电子受到磁场作用而产生电流的现象。
与此同时,电磁场理论探讨了电荷和电流产生的电磁场如何相互作用,相互影响。
本文将深入探讨电磁感应与电磁场理论相关的原理和应用。
一、电磁感应电磁感应是指当导体在磁场中运动,或磁场发生变化时,导体中的自由电子会受到力的作用而产生电流。
这一现象遵循法拉第电磁感应定律,即磁通量的变化率与感应电动势成正比。
这个定律可以用以下公式表示:ε = -dΦ/dt其中,ε代表感应电动势,Φ代表磁通量,t代表时间。
负号表示感应电动势的方向与磁通量变化的方向相反。
电磁感应广泛应用于发电机、变压器等电器设备中。
发电机通过旋转导体在磁场中切割磁力线,产生感应电动势和电流,进而转化为电能。
而变压器则利用电磁感应原理来改变交流电的电压大小。
二、电磁场理论电磁场理论是电磁学的基础理论之一。
根据麦克斯韦方程组,电磁场由电场和磁场组成,并且它们彼此相互依存、相互作用。
电场由带电粒子产生,而磁场则由电流产生。
电磁场理论的核心方程为麦克斯韦方程组,其中包括:1. 麦克斯韦第一和第二方程组成的电场方程:∇·E = ρ/ε0∇×E = -∂B/∂t其中,∇表示梯度运算符,E表示电场强度,ρ表示电荷密度,ε0表示真空介电常数,B表示磁感应强度,t表示时间。
2. 麦克斯韦第三和第四方程组成的磁场方程:∇·B = 0∇×B = μ0J + μ0ε0∂E/∂t其中,∇表示梯度运算符,B表示磁感应强度,J表示电流密度,μ0表示真空磁导率。
通过运用麦克斯韦方程组,我们可以推导出电磁波的性质,进一步探索电磁场的行为规律。
电磁场理论的应用非常广泛。
例如,电磁场理论在通信领域中的应用,我们利用电磁波传输信号,实现了无线通信。
此外,电磁场理论在电子技术、雷达、微波炉等方面也有许多重要的应用。
三、电磁感应与电磁场理论的联系电磁感应与电磁场理论密切相关。
第9章电磁感应电磁场理论9-1如图9-1所示,通过回路的磁感应线与线圈平面垂直,且指向图面,设磁通量依如下关系变化:φ=6t2+7t+1式中φ的单位为mWb,t的单位为s.求t=2时,回路中的感生电动势的量值和方向.图9-1解:由题意可知,回路中的感生电动势为:当时,电动势为:,方向为逆时针方向(即与设定的回路绕行t s2方向相反).9-2在两平行导线的平面内,有一矩形线圈,如图9-2所示.如导线中电流,随时间变化,试计算线圈中的感生电动势.图9-2解:根据题意建立坐标系,取坐标轴Ox,如图9-3所示.图9-3两电流在x处的磁感应强度大小为:,方向垂直纸面向里.取顺时针为回路的绕行方向,通过面元dS=l1dx的磁通量为:通过矩形线圈的磁通量为:矩形线圈中的感生电动势为:.9-3如图9-4所示,具有相同轴线的两个导线回路,小的回路在大的回路上面距离y 处,y远大于回路的半径R,因此当大回路中有电流,按图示方向流过时,小回路所围面积πr2之内的磁场几乎是均匀的.现假定y以匀速v=dy/dt而变化.(1)试确定穿过小回路的磁通量φ和y之间的关系;(2)当y=NR时(N为整数),小回路内产生的感生电动势;(3)若v>0,确定小回路内感应电流的方向.图9-4解:(1)根据导电线圈轴线上的磁感应强度分布,可得大回路在小回路处产生的磁感应强度:.由题意知,因此在距离大线圈平面y处的磁场可近似为均匀磁场,其次感应强度,则穿过小回路中的磁通量和y之间的关系为:.(2)小回路内产生的感生电动势为:.(3)由榜次定律可判定,当从上向下看时小回路的感应电流为逆时针方向.9-4PM和MN两段导线,其长均为10cm,在M处相接成30°角,若使导线在均匀磁场中以速度v=15m/s运动,方向如图9-5所示,磁场方向垂直纸面向内,磁感应强度为B=25×10-2T,问P、N两端之间的电势差为多少?哪一端电势高?图9-5解:由题意可知,P、N两端之间产生的动生电动势为:即运动导线上P端的电势高,N端电势低.9-5一均匀磁场与矩形导体回路面法线单位矢量e n间的夹角为θ=π/3(如图9-6),已知磁感应强度B随时间线性增加,即B=kt(k>0),回路的MN边长为l,以速度V向右运动,设t=0时,MN边在x=0处.求任意时刻回路中感应电动势的大小和方向.图9-6解:如图9-6所示,回路的面法线e n表明,回路的绕行方向为逆时针,则回路中感应电动势为:.又由题意知:则回路中感应电动势:方向由M指向N,即沿顺时针方向.9-6如图9-7所示,一长直导线通有电流,I=0.5A,在与其相距d=5.0cm处放有一矩形线圈,共1000匝.线圈以速度v=3.0m/s沿垂直于长导线的方向向右运动时,线圈中的动生电动势是多少?(设线圈长l=4.0cm,宽b=2.0cm.)图9-7解:由题意可知,线圈中的动生电动势为:.9-7如图9-8所示,导线MN在导线架上以速度V向右滑动.已知导线MN的长为50cm,V=4.0m/s,R=0.20Ω,磁感应强度B=0.50T,方向垂直于回路平面.试求:(1)MN运动时所产生的动生电动势;(2)电阻R上所消耗的功率;(3)磁场作用在MN上的力.图9-8解:(1)导线上产生的电动势为:.(2)电阻R上所消耗的功率为:.(3)由安培定理,可得回路中电流:导线MN上的安培力:,方向向左.9-8如图9-9所示,PQ和MN为两根金属棒,各长1m,电阻都是R=4Ω,放置在均匀磁场中,已知B=2T,方向垂直纸面向里.当两根金属棒在导轨上分别以v1=4m/s 和v2=2m/s的速度向左运动时,忽略导轨的电阻,试求:(1)两棒中动生电动势的大小和方向,并在图上标出;(2)金属棒两端的电势差;(3)两金属棒中点O1和O2之间的电势差.。
第九章 电磁场填空题 〔简单〕1、在竖直放置的一根无限长载流直导线右侧有一与其共面的任意形状的平面线圈,直导线中的电流由上向下,当线圈以垂直于导线的速度背离导线时,线圈中的感应电动势 ,当线圈平行导线向上运动时,线圈中的感应电动势 。
〔填>0,<0,=0〕〔设顺时针方向的感应电动势为正〕(<0, =0)2、磁场的高斯定律说明磁场是 ,因为磁场发生变化而引起电磁感应,是不同于回路变化时产生的 。
相同之处是 。
〔无源场,动生电动势,磁通量发生改变〕3、只要有运动电荷,其周围就有 产生;而法拉弟电磁感应定律说明,只要 发生变化,就有 产生。
〔磁场,磁通量,感应电动势〕4、一磁铁自上向下运动,穿过一闭合导体回路,〔如图7〕,当磁铁运动到a 处和b处时,回路中感应电流的方向分别是 和 。
〔逆时针,顺时针〕5、电磁感应就是由 生 的现象,其主要定律为 ,其中它的方向是由 定律来决定,即 。
〔磁,电,电磁感应定律,楞次,见p320〕6、当穿过某回路中的磁通量发生变化时,电路中 (填肯定或不肯定)产生感应电流;电路中 (填肯定或不肯定)产生感应电动势。
(不肯定, 肯定)7、在电磁感应中,感应电动势的大小与闭合回路的磁通量 成正比。
〔对时间的变化率〕8、在竖直放置的一根无限长载流直导线右侧有一与其共面的任意形状的平面线圈,直导线中的电流由上向下,当线圈平行导线向下运动时,线圈中的感应电动势 , 当线圈以垂直于导线的速度靠近导线时,线圈中的感应电动势 。
〔填>0,<0,=0〕〔设顺时针方向的感应电动势为正〕(=0,>0)9、将条形磁铁插入与冲击电流计串连的金属环中,有-5q=2.010c ⨯的电荷通过电流计,假设连接电流计的电路总电阻25R =Ω,则穿过环的磁通量的变化=∆ΦWb 。
〔4510q R --⨯=-⨯〕10、电磁波是变化的 和变化的 在空间以肯定的速度传播而形成的。
电磁感应练习题及解答电磁感应练习题及解答电磁感应是物理学中的一个重要概念,涉及到电磁场的变化过程中电场和磁场相互作用产生的现象。
它在日常生活和科学研究中都有广泛的应用。
下面是一些电磁感应练习题及解答,供大家进行练习。
1. 一根长导线以速度v从北向南方向通过均匀磁场B,该导线的两端分别连接一个电阻为R的电灯泡。
求当导线通过磁场过程中,电灯泡亮起的时间。
解答:根据法拉第电磁感应定律,导线通过磁场时产生感应电动势,导致电流流过电灯泡。
所以,在导线通过磁场期间,电灯泡会一直亮起。
因此,电灯泡亮起的时间等于导线通过磁场的时间。
2. 一个长方形线圈的边长为a和b,放置在匀强磁场B中,使得长方形线圈的法线与磁场方向垂直。
求长方形线圈在匀强磁场中的磁通量。
解答:根据法拉第电磁感应定律,在匀强磁场中,线圈的磁通量可以通过以下公式计算:Φ = B * A * cosθ,其中B表示磁场强度,A表示线圈的面积,θ表示磁场方向与线圈法线方向之间的夹角。
由于线圈的法线与磁场方向垂直,θ为0,所以磁通量Φ = B * A。
3. 在一个闭合导线中有一个直径为d的圆环,该圆环的电阻为R。
当一个恒定的磁场B垂直于圆环平面时,求圆环上感应的电动势。
解答:根据法拉第电磁感应定律,当磁场的变化导致一个闭合回路中的磁通量发生改变时,会在回路中产生感应电动势。
在这个问题中,磁场是恒定的,所以不会产生感应电动势。
4. 一个导线带有电流I,在该导线旁边有另一条导线,它们平行。
第二条导线的长度为L,并且距离第一条导线的距离为d。
求第二条导线中感应的电动势。
解答:当电流从第一条导线中流过时,会在周围产生磁场。
第二条导线因为位于磁场中,所以会感受到这个磁场产生的磁通量的改变。
根据法拉第电磁感应定律,第二条导线中的感应电动势可以通过以下公式计算:ε = -dΦ/dt,其中Φ表示磁通量的变化率。
在这个问题中,需要计算第二条导线中的磁通量的变化率,并由此得出感应电动势。
习题99-1在磁感应强度B 为0.4T 的均匀磁场中放置一圆形回路,回路平面与B 垂直,回路的面积与时间的关系为:S=5t 2+3(cm 2),求t=2s 时回路中感应电动势的大小? 解:根据法拉第电磁感应定律得dtd m Φ-=εdt dSB =Bt 10=V 4108-⨯=ε9-2 如题9-2图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环感应电动势的大小和方向及MN 两端的电压U M -U N .题9-2解: 作辅助线MN ,则在MeNM 回路中,沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε= 又∵ ⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2d cos 0πμπε 所以MeN ε沿NeM 方向,大小为ba ba Iv -+ln 20πμ M 点电势高于N 点电势,即ba ba Iv U U N M -+=-ln 20πμ题9-39-3 如题9-3图所示,在两平行载流的无限长直导线的平面有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以d Id t的变化率增大,求:(1)任一时刻线圈所通过的磁通量; (2)线圈中的感应电动势. 解: 以向外磁通为正则(1) ]ln [lnπ2d π2d π2000dad b a b Ilr l r Ir l r Iab b ad d m +-+=-=⎰⎰++μμμΦ (2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε题9-49-4 如题9-4图所示,长直导线通以电流I =5 A ,在其右方放一长方形线圈,两者共面.线圈长b =0.06 m ,宽a =0.04 m ,线圈以速度v =0.03 m/s 垂直于直线平移远离.求:d =0.05 m 时线圈中感应电动势的大小和方向.解: AB 、CD 运动速度v方向与磁力线平行,不产生感应电动势.DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针.9-5 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动.已知导轨处于均匀磁场B 中,B 的方向与回路的法线成60°角(如题9-5图所示),B 的大小为B =kt (k 为正常数).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向.题9-5图解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向.题9-6图9-6 一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B 的方向如题9-6图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0). 解: 如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε; 题9-6图(a)题9-6图(b)在磁场中时0d d =tΦ,0=ε; 出场时0d d >tΦ,0<ε,故t I -曲线如题9-6图(b)所示.9-7 导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动.aO=3l,磁感应强度B 平行于转轴,如题9-7所示.试求:(1) ab 两端的电势差;(2) a ,b 两端哪一点电势高?题9-7图解: (1)在Ob 上取dr r r +→一小段 则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高.9-8 北半球某地的磁场为4⨯10-5T ,磁场方向与水平方向成60o ,现将一根长1m 东西方向水平放置的均匀金属棒自由落下,求t=3s 时金属棒中感应电动势大小?解:根据动感电动势定义l d B v L⋅⨯=⎰)(ε自由下落,速度大小 gt v =,方向与重力加速度方向相同⎰⎰=⋅⨯=LLdl Bv l d B v 030sin )( ε 当t=3s 时,V L Bv 4010630sin -⨯==ε9-9 两根平行长直导线,横截面的半径都是a ,中心相距为d ,两导线属于同一回路.设两导线部的磁通可忽略不计,证明:这样一对导线长度为l 的一段自感为0L=In l d a aμπ-.题9-9图解: 如题9-9图所示,取r l S d d = 则 ⎰⎰-----=--=-+=ad aad aad da a d Il r r r Ilr l r Ir πI)ln (ln 2πd )d 11(π2d ))d (π22(0000μμμμΦ aad Il-=lnπ0μ ∴ aad lIL -==lnπ0μΦ9-10 两线圈顺串联后总自感为1.0 H ,在它们的形状和位置都不变的情况下,反串联后总自感为0.4 H.试求:它们之间的互感. 解: ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H题9-11图9-11 一矩形截面的螺绕环如题7-11图所示,共有N 匝.试求:(1)此螺绕环的自感系数;(2)若导线通有电流I ,环磁能为多少?解:如题7-11图示 (1)通过横截面的磁通为 ⎰==baab NIhr h r NIlnπ2d π200μμΦ 磁链 ab IhN N lnπ220μΦψ== ∴ ab hN IL lnπ220μψ==(2)∵ 221LI W m = ∴ ab hI N W m ln π4220μ=9-12 一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线部单位长度上所储存的磁能. 解:在R r <时 20π2RI B rμ=∴ 4222002π82Rr I B w m μμ== 取 r r V d π2d =(∵导线长1=l ) 则 ⎰⎰===RRm I Rrr I r r w W 0204320π16π4d d 2μμπ9-13 圆柱形电容器、外导体截面半径分别为R 1和R 2(R 1<R 2),中间充满介电常数为ε的电介质.当两极板间的电压随时间的变化为=k dUdt时(k 为常数),求介质距圆柱轴线为r 处的位移电流密度.解:圆柱形电容器电容 12ln 2R R lC πε=12ln 2R R lUCU q πε== 1212ln ln 22R R r U R R r lU S q D εππε===∴ 12ln R R r ktDj ε=∂∂=9-14 试证:平行板电容器的位移电流可写成d I =CdUdt.式中C 为电容器的电容,U 是电容器两极板的电势差.如果不是平板电容器,以上关系还适用吗? 解:∵ CU q =SCUD ==0σ ∴ CU DS D ==Φ不是平板电容器时 0σ=D 仍成立 ∴ tUCI D d d =还适用.9-15 半径为R =0.10 m 的两块圆板构成平行板电容器,放在真空中.今对电容器匀速充电,使两极板间电场的变化率为13=1.010dEdt⨯V/(m·s).求两极板间的位移电流,并计算电容器离两圆板中心联线r (r <R )处的磁感应强度B r 以及r =R 处的磁感应强度B R . 解: (1) tEt D j D ∂∂=∂∂=ε 8.22≈==R j S j I D D D πA(2)∵ S j I l H SD ld d 0⋅+=⋅⎰∑⎰取平行于极板,以两板中心联线为圆心的圆周r l π2=,则22d d 2r tE r j r H D πεππ== ∴ tEr H d d 20ε=tEr H B r d d 2000εμμ== 当R r =时,600106.5d d 2-⨯==tER B R εμ TtUC t ID D d d d d ==Φ。