二年级奥数 数数图形 教案
- 格式:docx
- 大小:1.07 MB
- 文档页数:5

(板书课题:图形规律)二、星海遨游[30分钟][一]星海遨游1[10分钟]找规律,选出第4幅图的图形编号。
①②③④师:同学们,用你们的火眼金睛观察下这道题,看看题中的四个图形大小、形状、数量等是否有什么相同或不同点呢?生:[思考]它们外形都是一个圆。
师:非常棒,这个是他们相同点,那他们不同点是什么。
生:里面阴影部分的图形在圆中的位置不一样。
师:果真是火眼金睛,那我们看看这个阴影部分的图形它在圆中的位置有没有一定的规律呢?生:[观察思考]师:第一个圆中阴影部分开口方向朝哪边?生:开口朝左。
师:那第二个圆中阴影部分开口方向又朝哪边?生:朝上。
师:第三个呢?生:朝右。
师:同学们,用手比划出前面三个圆中阴影部分开口朝的方向,先哪,到哪,再到哪?生:先左,再上,再右。
师:所以顺着下来,最后一个圆中阴影部分应该开口朝哪呢?生:朝下。
板书:选③。
[一]星海历练1[5分钟]看图形,找规律,第四幅图应该怎么画?分析:从前三个图形中可以知道方框内三角形数量不变,黑色三角形的位置发生变化,从右下往上,先右下角第一个涂黑--右下角往上第二斜列两个涂黑--右下角往上第三斜列两个涂黑--右下角往上第四斜列两个涂黑。
板书:[二]星海遨游2[10分钟]仔细观察下面图形变化规律,想一想第四幅图应该怎么画?师:同学们,你们按刚才老师教的方法,看下这里图形有哪些是变化的,哪些是不变的?生1:方框内四个小图形的数量和图形形状不变。
生2:四个小图形在方框内位置发生变化。
师:发生了怎样的变化呢?生:老师它们的位置都不是固定的,好难发现。
师:那我们把这个分成四格的方框标上序号,然后一个图形一个图形看看能否发现它们的变化规律。
师:老师把这个方框按这样的顺序标号。
[板书:]师:三角形的变化位置是按怎样的规律摆放的?生:4-1-2-空-4。
师:说明第四个图形中哪个方格内是放三角形的呢?生:第3个。
师:按这样的方法,看看正方形、圆形、长方形又是按怎样的规律摆放的。

老师一起来学习“图形找规律”。
【板书课题:图形找规律】二、探索发现授课(40分)(一)例题1(13分)根据前面3个图形的变化规律,画出第4个图形。
师:同学们,请你们仔细观察前面3个图形的变化规律,你们发现它们有什么相同点吗?生:前面3个图形相同点都是圆形,并且被分成了四部分。
师:非常棒!那有什么不同点呢?生:不同点在于它们蓝色图形的位置不同。
师:你观察得真仔细。
请你们仔细看看蓝色图形的位置,它是怎样变化的?生:第一个图形蓝色在左上方,第二个图形跑到了左下方,接着第三个图形跑到了右下方,第四个……应该跑到了右上方。
师:你同意他的说法吗?请你再来说一说。
生:我同意他的看法。
从图中我们知道蓝色图形应该是按逆时针走动的。
师:你真厉害!我们能够发现图中蓝色图形的位置是沿着逆时针方向一步一步变化的。
那第四个图形的蓝色部分应该在哪儿?生:在右上方。
师:很好!我们刚刚在观察图形的时候,是怎样观察的?生:先观察一下它们有什么相同的地方。
师:然后呢?生:然后再看不同的地方,找规律。
师:非常好!如果以后遇到像这样的图形找规律,先找到各个图形之间的不同点和共同点,要知道不同点是通过什么变化得来的。
板书:练习1(6分)根据前面3个图形的变化规律,画出第4个图形。
分析:根据前3个图形的变化规律,我们发现它们的相同点都是田字格的正方形;不同点在于红色圆点的位置沿着顺时针方向一步一步地变化。
所以按照这个规律,我们能够知道第四个图形红色圆点的位置在左下角的格子里。
板书:(二)例题2(13分)按照规律填出空白图形。
师:对于大部分同学来说,上一题的找规律简直是轻而易举。
接下来我们来挑战一下更有难度的题目,请你按照规律填出空白图形。
仔细观察前3幅图,你发现了什么?生:我发现了前3幅图中,每一幅都有圆形和三角形。
师:你的眼睛真锐利!每一幅图中都有圆形和三角形,谁还能观察的更仔细吗?先找到各个图形之间的不同点和共同点,然后再观察不同点是通过什么变化得来的。
第2讲我会数图形一年级我们已经认识了各种图形,并会数简单的图形.在这个基础上,本节课我们就将进一步深入的学习图形计数的方法.从简单的数线段的方法入手,拓展到数角、三角形、长方形、正方形等.通过数图形的练习,来让学生总结方法,找到计数的技巧.培养学生有序的思考问题的能力.知识点:1.掌握数规则的图形的个数的方法.(如线段、三角形、长方形等)1.教学点将给老师提供本节课的挂图.2.老师把每个图形制成图片.第2讲【教学思路】课前复习通过数简单的图形,使学生养成做记号的好习惯,为后面的学习奠定基础.⑴ 三角形有6个,正方形有3个,长方形有4个,椭圆形有8个.⑵ 正方形有4个,长方形有6个,三角形有3个,平行四边形有4个,圆形有5个.⑴下面的图各画了几个三角形、正方形、长方形和椭圆形?( )个三角形 ( )个正方形 ( )个长方形 ( )个椭圆形⑵ 这所漂亮的房子是用哪些图形拼成的呢?数一数.同学们,我们已经会数简单的图形,今天这节课我们将继续来学习数图形的方法.在数图形的时候,同学们要认真仔细,必须要做到按顺序、有条理、不遗漏、不重复得来数.这样我们在数图形的时候,才能数得又快又准.数一数,下图中有多少条线段?【教学思路】在一年级的时候,我们已经学过了数线段的基本方法,今天继续学习老师要引导学生把这种数图形,有方法, 要认真,别慌张.OEDC B AOE C( )条线段 ( )个角 ( )个三角形这些图形你会数吗?在数这些图形的时候,方法有什么相同和不同?方法进行推广和拓展.数线段有两种方法,具体分析如下:方法一:已知在两点间的直线部分就是一条线段,这两个点就叫做线段的端点,我们分别以不同端点为出发点按顺序数.⑴以A点为左端点的线段有:AB、AC、AD,共3条.⑵以B点为左端点的线段有:BC、BD,共2条.⑶以C点为左端点的线段有:CD,共1条.总共有:3216++= (条).方法二:如果把相邻两点间的线段叫做基本线段,即此图中AB、BC、CD是基本线段,我们也可从基本线段开始数.⑴由1条基本线段组成的线段有:AB、BC、CD共3条.⑵由2条基本线段组成的线段有:AC、BD共2条.⑶由3条基本线段组成的线段有:AD共1条.总共有:3216++= (条).总结方法:在数线段中,我们一定要抓住端点个数减1就是基本线段的条数来计算,而若有n个端点,线段总数则有12321()()条.-+-++++n n1.数一数,下面图形中有多少条线段?【教学思路】数一数一共有6个端点,那么基本线段就有615++++-=条,这个图中一共就有:54321 =(条)线段.152.在一条直线上画9个端点,可以数出(36)条线段.【教学思路】一共有9个端点,那么基本线段就有918-=(条),这个图中一共就有:8765432++++++ +=(条),可以数出36条线段.136数一数,图中共有多少个锐角?【教学思路】从图上可以看出,任意两条从O 点发出的射线都能组成一个角,先数以OA 为公共边的锐角有:∠AOB 、∠AOC 、∠AOD 、∠AOE ,共4个;以OB 为公共边的锐角有:∠BOC 、∠BOD 、∠BOE ,共3个: 以OC 为公共边的锐角有:∠COD 、∠COE ,共2个: 以OD 为公共边的锐角有:∠DOE ,共1个. 所以,锐角总数: 432110+++=(个).角的总数与射线的条数之间的关系:基本角(我们将相邻两条射线构成的角叫基本角)总比射线的条数少1,而角的总数应等于从1开始的一串连续自然数之和,其中最大的自然数等于基本角的个数.如果有1n +条射线,则有n 个基本角,而角的总数应等于12n n -+-+()() 321+++.数角方法也可推广到数三角形.数一数,图中有多少个三角形?【教学思路】数线段的方法也可以推广到数三角形,在这个图中一共有4个基本三角形,那么一共有432110+++=(个)三角形.数一数下图中有多少个长方形?OED C B AOEC【教学思路】注意到图中AD 上的每一条线段与宽都可以构成一个长方形.因此,AD 上有多少条线段就有多少个长方形,AD 上有线段:432110+++= (条),这10条线段都可以和宽AB 组成一个长方形,所以一共有10个长方形.数一数下图中有多少个长方形?【教学思路】上面第一层以AB 为宽的有10个长方形,下面第二层以BE 为宽的也就有10个长方形.另外把第一层和第二层合在一起以AE 为宽的长方形还有10个,一层有10个,共3层,这样一共就有10330⨯=(个)长方形.总结方法:数长方形时,分层数最简单,我们可以先数出一层有多少个,再数出有几层,长方形的个数就是:每层的个数×层数DCB AF E DCB A【教学思路】牧童指给秀才的是左边那条路.“句”字左边添一竖,念“向”,牧童的意思是向左边走.这些图形你会数吗?我们发现,在数图形时,如果图形比较复杂,就应观察能否将图形按某一位秀才赴京赶考.一日,他走到一处三岔路口,感到左右为难.正在这时,有一牧童路过此地,秀才忙上前向他问路.那牧童一句话也没说,只是低头用树枝在地上划了一个“句”字,起身便要离开.秀才以为牧童没有听清楚,不料牧童却指着地上的字说:“我不是已经告诉你了吗!”说完,扬长而去.秀才听了牧童的话,先是一愣,再看一眼牧童写下的这个字,高兴地上路了.你知道牧童指给秀才的是哪一条路吗?数一数,下图中共有多少个三角形?【教学思路】这个图形比较复杂我们可以分类来数,这样不会重复也不会遗漏.具体分析如下:⑴ 左边三角形ABD 中有3216++=(个)三角形; ⑵ 右边三角形ADC 中有3216++=(个)三角形; ⑶ 左右合起来三角形ABC 中有3个三角形; 一共有:66315++=(个)三角形.数一数,图中共有多少个三角形?【教学思路】这道题有两种分类的方法,分析如下:方法一:先看部分,再看整体.观察此图,发现三角形BCO 和三角形ACO 是相同类型的,所以我们仍可分为两类来研究.先看三角形BOC 中有213+=(个)三角形,所以CAO 中仍有3个三角形.最后看由三角形BCO 和三角形CAO 共同组成的三角形,有三角形ADB 和三角形AOB 共2个.所以此图三角形共有:3328++=(个). F EDCBAODCBA方法二:根据三角形包含基本三角形的个数来分类数.先数基本三角形有4个;再数包含两个基本三角形的三角形有3个,分别是三角形BOC、三角形AOC和三角形BDA;最后数包含四个基本三角形的三角形有1个,是三角形AOB.所以此图三角形共有:4318++=(个)如下图,数数有()个三角形.【教学思路】根据三角形包含基本三角形的个数来分类数,方法如下:分类数第一类(含1个基本三角形,最小的):1359++=(个);第二类(含4个基本三角形,次大的):3个;第三类(含9个基本三角形,最大的):1个.一共有93113++=(个)三角形.数一数,下图中共有多少个正方形?【教学思路】仔细观察,这个图形一共有三层.我们可以分层数,具体分析如下:最里面一层有5个正方形.中间一层有5个正方形.外面一层有5个正方形.合起来一共有55515++=(个)正方形.【教学思路】如果时间有限,拓展与提高可留为课后思考题.具体分析如下:⑴ 一共有30条线段.这个大五角星中有5条长线段,每条长线段上共可以数出:3216++=(条)线段,那么五角星中共有6530⨯=(条)线段.⑵ 一共有8个三角形.五角星的每个角上分别有1个小三角形,总共有5个;另外还有5个类似图中阴影的较大三角形,所以共有5510+=(个)三角形.(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)拓 展 与 提 高——巧 数 五 角 星蜘蛛妈妈织了一张漂亮的大网,如图所示.小蜘蛛想跟妈妈学织网,妈妈说:“要想学织网首先要弄明白这张网的结构.你先去数一数,这张网上有多少条线段,多少个三角形.”小蜘蛛数了半天,怎么也数不清,你能帮帮它吗?下面图中给出了五个点,在每两点之间画线段.一共可以画多少条?【教学思路】两点之间可以画一条线段.图中有5个点,每一点都可以向其他4点画线段,这样就可以画5420÷=(条)线段.⨯=条线段,但两点之间都算了两条线段,重复了,所以只能画20210数一数,下图中共有多少个小于180°角?【教学思路】用角的顶点和位置的变化进行分类:以A为顶点的角有∠BA0,∠DA0,BAD共3个,同理:以B、C、D为顶点的角各3个.以0为顶点的角有∠AOB,∠BOC,∠CDD,∠DOA共4个.图中共有小于180°角:34416⨯+= (个)数一数,下图中共有多少个三角形?【教学思路】图中共有44个三角形.其中最大的2个、次大的6个、次小的12个、最小的24个.1.数一数.o(10)条线段(6)个锐角2.数一数,图中有多少个三角形?(5)个(6)个(5)个3.图中有多少个正方形?(17)个(14)个4.数一数,图形中有几个长方形?5.数一数,下图中共有多少个三角形?【答案】根据三角形包含基本三角形的个数来分类数.只含有一个基本三角形的三角形有6个; 恰含两个基本三角形的三角形有3个; 恰含三个基本三角形的三角形有6个;恰含四个或五个基本三角形的三角形一个也没有;恰含六个基本三角形的三角形只有1个. 图中共有三角形:636116+++= (个).( 7 )个( 18 )个 ⑴⑵FEDCB A什么海没有鱼呢?一只蚂蚁可以从日本爬到中国,可能吗?什么牛不会拉车、耕地?什么东西落在水里却不会湿?把一只鸡和一只鹅放到冰箱里,结果鸡冻有一只羊,一年吃了草地上一半的草,问它死了,鹅却活着,这是为什么呢?把草全部吃光,需要多少年?平平把鱼放在鱼缸里,不到十分钟鱼都死在地上有100元钱和一块肉骨头,可是为什了,为什么?么努比拣起了肉骨头而没有拣钱呢?【答案】1.辞海、林海2.可能,在地图上爬3.蜗牛4.影子5.企鹅6.不能全吃光,因为草会年年生长的7.鱼缸里没有水8.努比是一只小狗十大环祸患威胁人类(二)六、化学污染工业带来的数百万种化合物存在于空气、土壤、水、植物、动物和人体中。

小学二年级奥数教案一、教学目标1、激发学生对数学的兴趣,培养他们主动思考和解决问题的能力。
2、帮助学生掌握一些基本的奥数思维方法,如逻辑推理、找规律、简单的图形变换等。
3、提高学生的数学运算能力和思维敏捷性。
4、通过有趣的奥数题目,增强学生的自信心和成就感。
二、教学重难点1、重点(1)培养学生观察、分析和解决问题的能力。
(2)让学生理解并掌握常见的奥数解题思路和方法。
2、难点(1)如何引导学生将抽象的数学问题转化为具体的、易于理解的形式。
(2)如何让学生在解决问题的过程中,灵活运用所学的知识和方法。
三、教学方法1、讲授法:讲解奥数的基本概念、方法和技巧。
2、练习法:通过大量的练习题,让学生巩固所学知识。
3、讨论法:组织学生讨论问题,激发他们的思维火花。
4、游戏法:通过有趣的数学游戏,提高学生的学习兴趣。
四、教学过程1、导入通过一个有趣的数学小故事或者一道简单的奥数题目,引起学生的兴趣,导入本节课的内容。
例如:“小明有 5 个苹果,小红的苹果数是小明的 2 倍还多 1 个,小红有多少个苹果?”2、知识讲解(1)逻辑推理讲解一些简单的逻辑推理题目,如“三个小朋友,小红、小明和小刚,小红说她不是最高的,小明说他比小红高,那么谁是最高的?”引导学生通过分析条件,得出结论。
(2)找规律展示一些数字、图形或者颜色的规律,让学生观察并找出规律,然后根据规律填空或者继续画图。
例如:“1,3,5,7,(),11” 让学生思考括号里应该填什么数字。
(3)简单的图形变换通过展示一些图形的平移、旋转、对称等变换,让学生认识图形的变化规律,并能够自己动手画出变换后的图形。
3、课堂练习给出一些与刚刚讲解的知识点相关的练习题,让学生在规定的时间内完成。
练习题的难度要适中,既能让学生巩固所学知识,又能让他们感受到一定的挑战。
4、小组讨论将学生分成小组,让他们讨论一些较难的题目,鼓励学生发表自己的看法和想法,互相交流解题思路。
5、讲解练习对学生完成的练习题进行讲解,重点讲解解题思路和方法,让学生明白自己错在哪里,如何改正。

《数图形的技巧》微课教学设计主备人:XXX教学目的:1、通过数简单个数的活动,让学生初步体会有序思考的必要性,并能运用有序的数法以及数图形的技巧数出或算出给定图形的个数。
2、在数图形的过程中做到不重复、不遗漏,发展学生的有序思维。
3、在数图形的过程中养成有序思考的习惯,激发学生的学习兴趣。
教学重难点:重点:有规律的数,不重复、不遗漏。
难点:发展并掌握数图形(长方形和平行四边形)的技巧。
教学过程:同学们好,欢迎来到“数学”微课堂!我是木塔寨小学的王老师,今天我们将一起来学习“数图形”的技巧。
一、复习导入同学们,在前面的学习中我们已经认识了长方形、正方形、平行四边形等一些基本图形,当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形,这节课我们就来探索数长方形有哪些技巧吧。
二、探究新知1、数线段(出示经典例题1)首先一起来看老师带来的例题1,先来读题,题目要求是让大家数一数一共有多少条线?同学们注意在数的时候一定要做到按顺序来数。
那么按一定的顺序数,我们可以得到以下信息:从A点出发的不同线有4条:AB、AC、AD、AE;(图示)从B点出发的不同线有3条:BC、BD、BE;(图示)从C点出发的不同线有2条:CD、CE;(图示)从D点出发的不同线有1条:DE(图示)o这样数完之后我们发现数的过程中没有重复,也没有遗漏。
因此,将刚才数出来的线依次相加就可以发现一共有10条。
我们来把这道题规范解答,先写出算式4+3+2+1=10(条),然后写出答语,答:一共有10条线。
2、数图形(出示经典例题2)接下来难度升级,这道题可把老师难住了,聪明的同学们快快开动脑筋,帮老师想一想吧。
先来读题,题目要求是数一数,一共有多少个长方形?你有什么方法吗?淘气提醒大家在数长方形的个数时要有顺序,做到不重复、不遗漏。
(-)笑笑是按这样的顺序数的,一起来看看吧。
她先数的是单个的长方形,(数)一共数出来了6个;笑笑接下来数的是由2个长方形组成的大长方形,(数)一共数了7个;按这样的顺序同学们应该已经猜到了接下来笑笑数的应该是由3个长方形组成的大长方形(数),一共数了2个;继续数,这时候3个接下来应该是4个,所以笑笑应该数的是由4个长方形组成的大长方形(数),一共数了2个,那大家想一想在我们这道题中,5个长方形能组成一个大的长方形吗?显然是不可以的,所以笑笑紧接着数的是由6个长方形组成的大长方形(数),一共数了1个。

数图形教案(5篇)第一篇:数图形教案《有序数图形》教学设计教学目标:1、通过数图形的个数,使学生体会到按一定规律去数,就会不重复、不遗漏,让学生体验有序的数法,养成有序思考的习惯。
2、在探求知识的过程中,逐步培养学生独立思考、合作探究、自主获取知识的能力。
教学重点:发展学生的有序思维。
教学难点:让学生掌握数图形的方法,做到不重复,不遗漏。
教学过程一、激发兴趣,导入新课:两个小朋友在教室干什么呢,我们一起去看一看!Ppt出示情境图提出问题:窗户上一共有几个长方形呢?二、自主探究、小组合作交流师:其实图形在我们的生活中无处不在,瞧,这窗户上有吗?有什么图形?你能数出窗户上有多少个长方形吗?师:提的真好,那现在就让我们一起去解决吧!拿出老师发的导学案,完成探究一,同学们,开始行动吧!师:哪位同学愿意说一说自己的想法。
三、学生展示,共同建构新知师:老师现在变一个魔术,当变成这样的一个窗户后,你能数出窗户上有多少个长方形吗?完成探究2,在开始之前老师有几个小小的建议,想不想听一下?同学们,开始行动吧!1、学生展示,产生分歧后达成一致师:好,交流结束。
我看同学们刚才讨论的特别热烈,想必你们已经有了自己的答案了,现在我们就找同学到前面来展示,为了让每个同学都能看清楚,老师把你们手中的窗户模型放大了,上台的同学可以用这个大图形来展示。
听清老师的要求,上来的同学先说一说你一共数出了几个长方形,再说一说你是怎样数的,台下的同学可要认真听哦,一会你们还要当小法官呢!哪位同学愿意先来试一试?第一位小勇士,你来。
学生自由展示。
师:看来同学们的答案有()种,…小法官们,考验你们的时候到了,你们同意哪种答案啊?师:同意有6个长方形的请举手,那么多同学同意6个啊?刚才说()个和()个的同学,你们同意吗?那你能说说你刚才漏数了那几个长方形吗?师:数()个和()个的同学,都漏数了这样的由2个小长方形组成的大点的长方形。
2、探究数法,引出有序数图形师:看来咱们同学都是合格的小法官,都判断出了窗户中一共有6个长方形,那咱们再来想一想,在数图形的时候,怎样才能不犯刚才漏数的错误呢?你在数的时候有什么好办法吗?同桌之间互相交流一下。

第2讲数数图形【专题简析】我们已经认识了线段、角、三角形、长方形等基本图形,当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。
要想准确地计数这类图形中所包含的某一种基本图形的个数,就需要仔细地观察,灵活地运用有关的知识和思考方法,掌握数图形的规律,才能获得正确的结果。
要准确、迅速地计数图形必须注意以下几点:1,弄清被数图形的特征和变化规律。
2,要按一定的顺序数,做到不重复,不遗漏。
【例1】:数出下面图中有多少条线段。
分析与解答:要正确解答这类问题,需要我们按照一定的顺序来数,做到不重复,不遗漏。
从图中可以看出,从A点出发的不同线段有3条:AB、AC、AD;从B点出发的不同线段有2条:BC、BD;从C点出发的不同线段有1条:CD。
因此,图中共有3+2+1=6条线段。
.练习1:数出下列图中有多少条线段。
答(1)(2)(3)例2:数一数下图中有多少个锐角。
分析与解答:数角的方法和数线段的方法类似,图中的五条射线相当于线段上的五个点,因此,要求图中有多少个锐角,可根据公式1+2+3……(总射线数-1)求得:1+2+3+4=10(个).练习2:下列各图中各有多少个锐角?答.例3:数一数下图中共有多少个三角形。
分析与解答:图中AD边上的每一条线段与顶点O构成一个三角形,也就是说,AD边上有几条线段,就构成了几个三角形,因为AD上有4个点,共有1+2+3=6条线段,所以图中有6个三角形。
练习3:数一数下面图中各有多少个三角形。
答例4:数一数下图中共有多少个三角形。
分析与解答:与前一个例子相比,图中多了一条线段EF,因此三角形的个数应是AD和EF上面的线段与点O所围成的三角形个数的和。
显然,以AD上的线段为底边的三角形也是1+2+3=6个,所以图中共有6×2=12个三角形。
.练习4:数一数下面各图中各有多少个三角形。
答.例5:数一数下图中有多少个长方形。
分析与解答:数长方形与数线段的方法类似。
可以这样思考,图中的长方形的个数取决于AB 或CD边上的线段,AB边上的线段条数是1+2+3=6条,所以图中有6个长方形。

《数图形》(教案)二年级上册数学青岛版在今天的数学课上,我们将一起探索《数图形》这个主题。
我们将使用青岛版二年级上册的数学教材。
一、教学内容我们将会学习第五章《数图形》的内容。
这部分包括:认识长方形、正方形,了解它们的特征;学会通过数图形的方法来认识它们;能够用语言描述图形的特征。
二、教学目标通过本节课的学习,我希望孩子们能够:1. 认识长方形和正方形,理解它们的特征;2. 学会通过数图形的方法来认识长方形和正方形;3. 能够用语言描述长方形和正方形的特征。
三、教学难点与重点重点:认识长方形和正方形,理解它们的特征。
难点:学会通过数图形的方法来认识长方形和正方形,能够用语言描述长方形和正方形的特征。
四、教具与学具准备教具:长方形和正方形的卡片,数图形的工具。
学具:每组一张长方形和正方形的卡片,数图形的工具。
五、教学过程1. 引入:我会通过展示长方形和正方形的实物卡片,让孩子们观察并说出它们的特征。
2. 讲解:我会用数图形的工具,展示如何通过数图形的方法来认识长方形和正方形。
3. 练习:孩子们将会用学具,尝试自己数图形,并描述长方形和正方形的特征。
六、板书设计板书设计将会包括长方形和正方形的特征,以及数图形的方法。
七、作业设计作业题目:请孩子们用数图形的方法,找出生活中的长方形和正方形,并描述它们的特征。
答案:孩子们需要找出生活中的长方形和正方形,并描述它们的特征。
八、课后反思及拓展延伸课后,我会反思孩子们在课堂上的表现,以及他们对长方形和正方形的理解程度。
对于那些还没有完全掌握的孩子,我会考虑如何在课后给予他们更多的帮助。
同时,我也会鼓励孩子们在生活中多观察长方形和正方形,加深他们对这些图形的理解。
通过本节课的学习,我希望孩子们能够掌握长方形和正方形的特征,学会用数图形的方法来认识它们,并能够用语言描述它们的特征。
重点和难点解析在今天的数学课上,我们将一起探索《数图形》这个主题。
我们将使用青岛版二年级上册的数学教材。

别有几个?师:你们知道什么叫做一笔画图形吗?生:可以一笔就画成的!师:说的还不是很完全,还有谁来补充一下?生:……师:刚刚我们画的图形有没有重复的线?生:没有!师:我说你们刚刚画的图形都是一笔画图形,你们能说说它们除了一笔画成的特点,还有没有其他的特点?生:有!它们的线都是没有重复的!师:非常棒!这就是一笔画图形中隐含的特点,我们能够一笔画成,而且每条线上都只画一次不重复的图形叫做一笔画图形。
仔细观察这些图形,试一试,有哪些图形一眼就可以看出来是不可以一笔画成的?生:第2个和第4个图形师:为什么呢?生:这两个图形当中的一些图形没有连在一起,所以不能一笔画成。
师:也就是说,这两个图形不是连通的,就是不能一笔画成的?生:是的!师:非常好!不连通的图形是不可能一笔画成的,那这里面哪些图形是可以一笔画成的呢?生:除了这两个,其余的都可以一笔画成!师:看样子你们都试过了,是可以一笔画成的。
第二个问题又来了,让我们数一数单数点和双数点的个数,你们知道什么是单数点,什么是双数点吗?生:[学生猜测,给出一些答案,大意差不多就可以给出肯定]师:双数点就是从一点出发的线的条数是双数,这点称为双数点。
那么单数点呢?生:从一点出发的线的条数是单数,这点称为单数点。
师:没错,我们一起数一数,这些图中的单数点和双数点分别有多少个呢?生:[开始数双数点与单数点的个数,教师巡视]师:同学们对双数点和单数点的理解的还不错,只是数数的时候一定不要粗心哦!你们数的个数都是一样的吗?生:是的!师:问题咱们已经解决了,再想想,它这里问能否一笔画,后面又接着问双数点和单数点的个数,这两者之间会不会有什么关系呢?板书:单数点:2个 0个 2个 2个双数点:2个 6个 5个 2个能否一笔画成:能不能能不能能能练习1[6分]试着用一笔画的方式画出3个图形,数一数它们分别有几个双数点,几个单数点?分析:注意一笔画的图形一定是连通的,可以是直线的也可以是曲线的。

小学奥数数数图形教案第一篇:小学奥数数数图形教案我是闯关小达人关卡一:握手游戏有6个小朋友,每2人握一次手并且只能握一次手,一共要握几次手?关卡二:你知道怎么算吗从青岛到上海的直达列车,中途停靠5个大站,这趟列车共有多少种不同的车票?关卡三:和爸爸妈妈合影如果让你和爸爸妈妈一起并排站着合影,你知道你们有几种不同的排列顺序吗?关卡四:我不会上当的哦老师在黑板上写下了0,2,4,6这四个数字,请同学们想想它们能组成几个三位数?数数图形教案例1:数一数,图中有多少个锐角?如何做到不重复又不遗漏呢?第一种方法:列举法第二种方法:图示法小朋友们,你们发现什么规律了吗?例2:数一数,下面图形中共有几个三角形?(1)(2)方法解析:按照三角形的拼组方式或者形状的大小将给定的图形分类数数。
(1)(2)例3:动动脑,数数下图中有几个长方形?例4:数数下图中有几个正方形?例5:数一数,下图中的大长方体是由多少个小长方体组成的?例6:下图所示的“塔”由四层没有缝隙的小立方块垒成,求塔中共有多少个小立方块?练习1.你知道下图中共有几个角吗?(1)(2)2.数一数,下面的图形有几条线段?(1)(2)3.你知道下图中共有几个三角形吗?(1)(2)4.下面图形有多少个长方形?(1)(2)5.下图是由小立方块码放起来的,其中有一些小立方体被压住看不见,请你数一数共有多少小立方体?第二篇:四年级奥数-数数图形-教案四年级奥数第十三章《数数图形》教案教学目标:1、在学过一些基本的几何图形的基础上,通过观察掌握数线段、角、三角形、长方形的规律和方法。
2、学生通知亲身体验明白数图形时不重复、不遗漏的规律,锻炼数学思维的严谨性。
教学重、难点:在观察的基础上,自己总结出数图形的规律和方法。
教学过程:一、复习:复习以前所学的数简单的线段、三角形、角的方法。
二、新授:例1:数一数,下图中有多少条线段?(1)(2)解答:(1)4+3+2+1=10(条)答:有10个线段。
第6课数数图形教学目标:1、弄清被数图形的特征和变化规律。
2、要按一定顺序数,做到不重复、不遗漏。
教学重难点:能按照一定的顺序数图形。
教学过程师:听说我们班的同学数图形可厉害了,一数一个准,今天余老师带来了一些图形,可把余老师数糊涂了,你们能帮余老师数一数吗?例1:数一数,下图中共有多少条线段?练1:观察下图,数一数图中有多少条线段?2、德清到杭州的公交车,除起点、终点外,还要停靠4个站,汽车公司要准备几种车票?例2:数出下列图中有几条线段?练2: (1)数一数,下图中有多少线段?%(2)小红在纸上画了一条线段,小亮又拿起笔,在小红画的线段上点了2个点,你知道现在这条线段上又多出了多少条线段吗?例3:数一数,下图中有多少个三角形?练3:数一数下列各图中有多少个三角形?3面涂成红色的小方块有( )个; 4面涂成红色的小方块有( 5面涂成红色的小方块有()个; )个。
练4:数数下图中有几个正方形?例5:将9个小方块组成一个“工”字形(如图),再将它的表面涂 成红色,然后把小方块分开,问:例4:数I练5:下图是将27个小方块堆成的一个正方体。
如果把它的表面涂上红色,问:3面涂成红色的小方块有()个;2面涂成红色的小方块有()个;1面涂成红色的小方块有()个。
数数图形(拓展卷)1、从南京到南通的一列火车,除起点、终点外,还要停靠7 个站,火车站要准备几种车票?2、数一数图中有多少个三角形?3、有6个点不在同一条直线上,每两点之间画一条线段,一共可以画多少条?4、将30个小方块堆成一个长方体(如图),如果把它的表面涂上红色,然后把小方块分开,问:2面涂成红色的小方块有(3面涂成红色的小方块有(1面涂成红色的小方块有()个; )个; )。
二年级下册数学教-1.1:用图形数数一、教学目标1.了解图形及其属性;2.掌握用图形计数的方法;3.提高学生的观察能力和逻辑思维能力。
二、教学重难点1.图形计数;2.各种形状的特征及联系。
三、教学准备1.教学用具:白板、彩色粘纸、图形卡片等;2.教材:二年级下册数学。
四、教学过程1.导入今天我们要学习的是用图形数数,我们日常生活中所接触到的很多东西都是由图形组成的,通过学习,我们可以更好地了解这些图形及其属性,提高我们的观察能力和逻辑思维能力。
2.新课讲解(1)数一数老师拿出不同形状的卡片,让学生们观察并记住。
老师把所有的图形放在桌子上,让学生数一数每种形状的图形有几个。
(2)选一选老师把几种不同形状的图形卡片放在桌子上,让学生选出其中某一种形状的图形。
(3)填空老师把几个图形卡片放在桌子上,让学生填空,例如:“桌子上有(三角形)个三角形。
”(4)连线老师把图形卡片和数字卡片分开放在桌子上,让学生把相同数量的图形和数字卡片连线。
3.教学练习:练习让学生掌握图形计数的方法。
(1)带着问个问题老师可以选出一些图形来,让学生通过问题,计算每种形状的图形有几个。
例如:“在桌子上,有几个红色的正方形?”(2)填图形老师可以在黑板上绘制一个图形表格,让学生填写每个图形的数量。
例如:形状|数量-- | --正方形|3三角形|5长方形|2圆形|44.教学拓展:让学生自己动手制作图形。
学生们可以运用彩色纸或粘纸制作各种图形,并在教师的帮助下,进行计数和比较。
五、作业布置让学生回家寻找各种图形,计算每种图形的个数,并画出图形表格。
六、教学反思通过本节课的学习,学生们能够了解到不同图形的特征和联系,在数学计数的过程中也增加了观察力和思维能力,同时在实践中也锻炼了他们的动手能力。
一、计算题。
( 共101题)1.图2-26是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
2.在图2-24中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
3.图2-23中有三个大圆,在大圆的交点上有六个小圆圈。
请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14。
4.将2、4、6、8、10、12、14、16、18填在下面图表,使每一横行、竖行、斜行的三个数相加的和都相等。
5.仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图?6.请看下图,共有多少个正方形?7.仔细观察这些图案可以发现,他们是按照下面这5个图案为一组,循环往复排列的,请问第52个图形是什么?8.把上面一排的立体图形剪开,可以剪成下面哪种图形的样子?动手试一试。
9.请把下图中长方形分成形状相同、大小相等的两块,然后再拼成一个正方形.10.在空格中填入合适的数11.下图表示"宝塔",它们的层数不同,但都是由一样大的小三角形摆成的。
仔细观察后,请你回答:(1)五层的"宝塔"的最下层包含多少个小三角形?(2)整个五层"宝塔"一共包含多少个小三角形?(3) 从第(1)到第(10)的十个"宝塔",共包含多少个小三角形?12.数一数,有( )个长方形。
13.请你将下面图形分成形状大小相同的四部分,你能行吗?14.请你将下面的图形拼成一个大长方形的宣传板,上面从左到右写着"快乐学习"几个字。
请你在大长方形图中将这几个字表示出来。
15.你能将下面的图形分成形状大小相同的四部分吗?其中AB=AD=EF=BC,DE=FC16.如图有5个点,在两个点之间可以画出一条线段,画出的图形中一共可以得到( )条线段.17.将14个大小一样的小正方体摆成下面的图形,然后将表面涂成红色再分开,有( )个小正方形的面没有被涂色。
奥数教案二年级教案标题:奥数教案二年级教案概述:本奥数教案适用于二年级学生,旨在培养学生的数学思维能力、逻辑思维能力以及问题解决能力。
通过有趣的数学问题和活动,激发学生对数学的兴趣,并帮助他们建立数学基础。
教案目标:1. 培养学生对数学的兴趣和热爱;2. 培养学生的数学思维能力和逻辑思维能力;3. 培养学生的问题解决能力和创造力;4. 建立学生的数学基础。
教案内容和活动:活动一:数学游戏 - 数字拼图1. 准备一组数字拼图,将数字1-9分成9个小块,打乱顺序。
2. 学生通过移动数字块,将数字拼图还原为顺序排列。
3. 引导学生观察数字拼图的特点,思考如何移动数字块才能还原拼图。
4. 提问学生,有哪些规律可以帮助还原拼图?活动二:数学竞赛 - 数字填空1. 准备一些有空缺的数字序列,例如:1, 2, _, 4, 5, _, 7, 8, _。
2. 学生根据数字序列的规律,填写正确的数字。
3. 鼓励学生思考数字序列的规律,例如递增、递减、奇数、偶数等。
4. 提问学生,下一个数字是多少?为什么?活动三:问题解决 - 数字组合1. 提供一些数字卡片,例如:1, 2, 3, 4。
2. 学生根据卡片上的数字,尝试组合出不同的两位数和三位数。
3. 引导学生思考数字组合的规律,例如个位数和十位数的关系,百位数的作用等。
4. 提问学生,如何用这些数字组合出一个大于10的两位数?三位数呢?活动四:创造力发散 - 数学故事1. 鼓励学生发挥想象力,创造一个有关数学的故事。
2. 学生可以选择故事的主题,例如数学竞赛、数学王国等。
3. 学生需要在故事中运用数学知识和概念,例如加减法、形状、数列等。
4. 学生可以口头或书面方式分享自己的数学故事。
教案评估:1. 观察学生在数学游戏中的表现,是否能够观察规律并还原数字拼图。
2. 检查学生在数学竞赛中填空的准确性和思考过程。
3. 评估学生在问题解决活动中的数字组合能力和解释规律的能力。
二年级奥数一图形数一数知识定位本课程主要让学生学会基础的数线段和图形的方法。
其中图形包括平面图形和立体图形。
要求学生掌握基本的对称法、分类法、公式法等方法。
知识梳理1、线段的数法:对单一一条线段上的线段数法,先找出基本线段的条数,基本线段即线段上除了端点以外不含其他端点的线段,之后将条数依次减1直到1后相加例如基本线段条数为4则总共有4+3+2+1=10条线段。
2、对称图形的数法:对左右对称的图形,只需要数左边后再乘2,然后再数是否有同时包含左右两边图形的符合要求的图形。
再将所得相加。
3、立体图形的数法:立体图形的难点在于求被遮住部分的个数,计算数目则通过与上面或者相邻可见图形进行对比求得。
因上层的个数比下层少,一般采用从上往下数,先算第一层有多少个,之后第二层比第一层多的那些正方体应该是可见的,因此第二层个数直接用第一层个数加上多出来的可见正方体个数,在讲解过程中可以通过让学生了解上面的每一个正方体下方都必须有一个正方体托住否则会掉落下一层来理解。
4、分类法:先找出基本的小图形,之后根据组成的小图形个数分类,将每一类个数求总。
知识导图线段的教法[翁习+拓展]对称图形的敷法立体图形的数法其它的教图形题目例题精讲:【题目】(1)下图中有多少条线段呢?A B D【题目】⑵下图中有多少个三角形呢?【题目】⑶下图中有多少个长方形呢?,八Je e U eAs【题目】下面图形的线段总数你会数吗?试试看吧!【题目】请你来数一数下面三角形和长方形的个数分别有多少个?【题目】我们都知道,数图形的基本思想是分类数图形。
那么,你能清楚的数出下面的图形中圆形,三角形和长方形(包括正方形)的个数分别是多少呢【题目】我们已经数过了平面图形的个数,下面让我们来数数立体图形的个数!聪明的小朋友们,下面的题目你们来试试吧!数一数每个图形中的小正方体的个数是多少?【题目】聪明的小朋友们,下面的题目你们来试试吧!数一数每个图形中正方形的个数是多少个。
二年级奥数教案教案一:数的顺序关系教学目标:1. 学生能够准确地理解数的顺序关系,包括大于、小于和等于。
2. 学生能够通过比较数的大小,正确排序一组给定的数。
3. 学生能够灵活运用数的顺序关系,解决简单的问题。
教学准备:教师准备:1. 模拟奥数习题集。
2. 黑板、粉笔。
学生准备:1. 数字卡片。
2. 笔和纸。
教学过程:步骤一:导入(5分钟)教师向学生介绍数的顺序关系,例如:大于、小于和等于。
通过与学生互动的方式,让学生理解这些概念,并从身边的例子中找到相关问题。
步骤二:探究(15分钟)教师给学生出示一组数字卡片,要求学生按照从小到大的顺序进行排列,并解释他们的思考过程。
教师在黑板上记录学生的答案,并与全班讨论。
步骤三:练习(20分钟)教师将学生分成小组,每组给出一组数字,要求他们按照从小到大的顺序进行排列,并写下他们的排序方法。
教师在黑板上挑选几组学生的答案进行讨论。
步骤四:拓展(10分钟)教师让学生尝试解决一些简单的数学问题,例如:找出一个数的前后两个数,或根据给定的条件确定一个数的范围。
鼓励学生用数的顺序关系进行推理和解答。
并在黑板上记录学生的思考过程,以促进学生之间的讨论和交流。
步骤五:总结(5分钟)教师和学生一起回顾这节课的学习内容,强调数的顺序关系的重要性,并总结学生们掌握的知识和技能。
教案二:数的运算教学目标:1. 学生能够准确地进行两位数的加法和减法运算。
2. 学生能够通过解决实际问题,应用数学运算。
3. 学生能够利用奥数思维解决一些简单的数学题目。
教学准备:教师准备:1. 模拟奥数习题集。
2. 黑板、粉笔。
学生准备:1. 数字卡片。
2. 笔和纸。
教学过程:步骤一:导入(5分钟)教师通过回顾前几节课学习的内容,引导学生复习两位数的加法和减法运算。
并提出一个实际问题,让学生思考如何用数学运算解决。
步骤二:探究(15分钟)教师给学生出示一道奥数题目,要求学生利用已学的数学运算方法解答。
第6课数数图形
教学目标:1、弄清被数图形的特征和变化规律。
2、要按一定顺序数,做到不重复、不遗漏。
教学重难点:能按照一定的顺序数图形。
教学过程
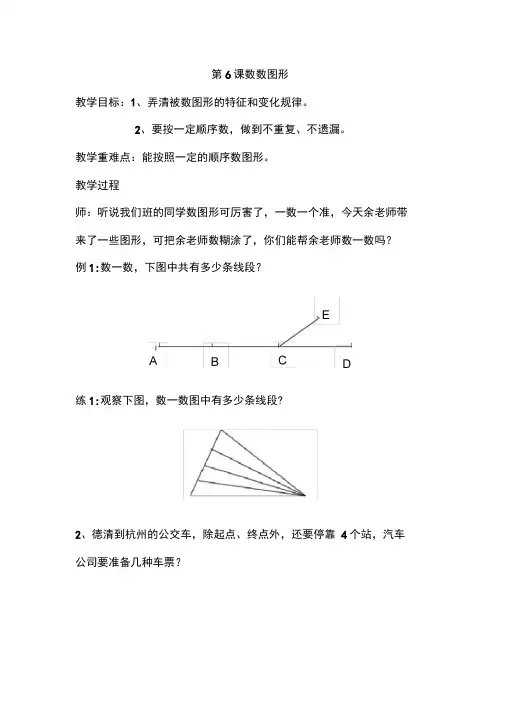
师:听说我们班的同学数图形可厉害了,一数一个准,今天余老师带来了一些图形,可把余老师数糊涂了,你们能帮余老师数一数吗?例1:数一数,下图中共有多少条线段?
E
A B C D
练1:观察下图,数一数图中有多少条线段?
2、德清到杭州的公交车,除起点、终点外,还要停靠4个站,汽车公司要准备几种车票?
例2:数出下列图中有几条线段?
练2:(1)数一数,下图中有多少线段?
①②
(2)小红在纸上画了一条线段,小亮又拿起笔,在小红画的线段上点了2个点,你知道现在这条线段上又多出了多少条线段吗?
例3:数一数,下图中有多少个三角形?
练3:数一数下列各图中有多少个三角形?
()个()个
( )个 ( )个
例4:数一数,下图中共有多少个正方形?
练4:数数下图中有几个正方形?
例5:将9个小方块组成一个“工”字形(如图),再将它的表面涂成红色,然后把小方块分开,问:
3面涂成红色的小方块有( )个;
4面涂成红色的小方块有( )个;
5面涂成红色的小方块有( )个。
① (1) ②
( )个
( )个 (2)
练5:下图是将27个小方块堆成的一个正方体。
如果把它的表面涂上红色,问:
3面涂成红色的小方块有()个;
2面涂成红色的小方块有()个;
1面涂成红色的小方块有()个。
数数图形(拓展卷)
1、从南京到南通的一列火车,除起点、终点外,还要停靠7个站,火车站要准备几种车票?
2、数一数图中有多少个三角形?
3、有6个点不在同一条直线上,每两点之间画一条线段,一共可以画多少条?
4、将30个小方块堆成一个长方体(如图),如果把它的表面涂上红色,然后把小方块分开,问:
2面涂成红色的小方块有()个;
3面涂成红色的小方块有()个;
1面涂成红色的小方块有()个。