七年级上册第一章

初一上册第1章总结知识点
本章主要介绍了科学与科学实践的基本概念，包括科学的概念、科学实践的基本特点、科
学研究的基本方法等内容。

通过本章的学习，使同学们对科学有了更深入的了解，对科学
实践有了更清晰的认识，为以后更好地学习科学知识、进行科学实践打下了良好的基础。

1.1 科学的概念
科学是一种寻求真理的理性活动。

它是通过实践活动对客观世界进行观察、实验和理论构建，从而揭示客观规律和规律性的认识活动。

科学的产生和发展是人们认识世界、改造世
界的重要手段。

科学是寻求真理的过程，它包括了对现象、规律、机理、方法等方面的认识。

1.2 科学实践的基本特点
科学实践是验证科学理论的最终标准。

科学实践的基本特点包括：客观性、系统性、可验
证性、可预测性、可控制性和可重复性等。

这些特点是科学实践持续发展和提高科学认识
水平的重要保证。

1.3 科学研究的基本方法
科学研究的基本方法包括了实验、观察、模型建立、推理等。

其中，实验是科学研究中最
重要的手段之一，它是对自然界进行人为干预的过程，是获取科学知识的有效途径。

总之，初一上册第一章的内容涉及了科学概念、科学实践的基本特点以及科学研究的基本
方法等方面，对学生们初步了解科学、认识科学研究方法和发展规律，打下了良好的基础。

希望同学们能够在以后的学习中不断提高科学素养，树立正确的科学观，自觉尊重科学、
学习科学、使用科学，不断完善自己，为将来成为全面发展的社会主义建设者和接班人做
好准备。

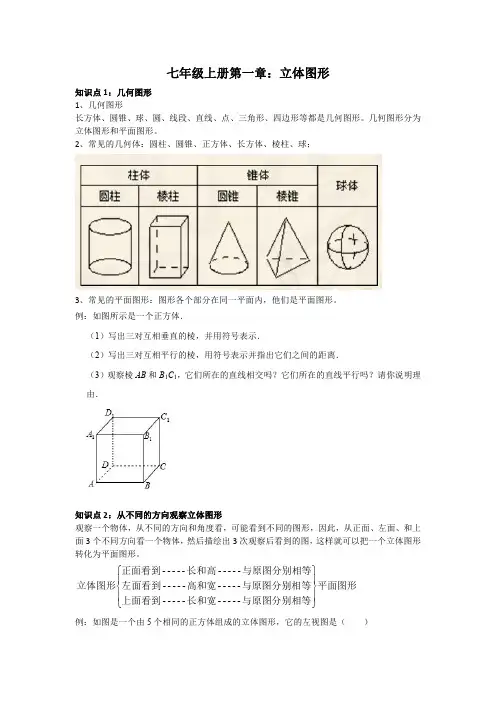
七年级上册第一章：立体图形知识点1：几何图形1、几何图形长方体、圆锥、球、圆、线段、直线、点、三角形、四边形等都是几何图形。

几何图形分为立体图形和平面图形。

2、常见的几何体：圆柱、圆锥、正方体、长方体、棱柱、球；3、常见的平面图形：图形各个部分在同一平面内，他们是平面图形。

例：如图所示是一个正方体．（1）写出三对互相垂直的棱，并用符号表示．（2）写出三对互相平行的棱，用符号表示并指出它们之间的距离．（3）观察棱AB 和B 1C 1，它们所在的直线相交吗？它们所在的直线平行吗？请你说明理由．知识点2：从不同的方向观察立体图形观察一个物体，从不同的方向和角度看，可能看到不同的图形，因此，从正面、左面、和上面3个不同方向看一个物体，然后描绘出3次观察后看到的图，这样就可以把一个立体图形转化为平面图形。

平面图形与原图分别相等长和宽上面看到与原图分别相等高和宽左面看到与原图分别相等长和高正面看到立体图形⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧------------------------------例：如图是一个由5个相同的正方体组成的立体图形，它的左视图是（）A．B．C．D．知识点3：立体图形的展开图1、定义：有些立体图形是由平面图形围成的，将他们的表面适当剪开，可以展开成平面图形，这样的平面图形称为相应立体图形的展开图。

2、正方体的展开图正方体的表面展开图有11种不同的形式，可以概括为4种基本类型：（1）一四一型（2）二三一型（3）三三型（4）二二二型例1如图是一个正方体展开图，把展开图折叠成正方体后，“最”字一面的相对面上的字是（）A．能B．我C．行D．棒例2．下列平面图形不能够围成正方体的是（）A．B．C．D．知识点4：点、线、面、体1、从运动的观点看，点动成线，线动成面，面动成体（1）点动成线：线是由无数个点组成的（2）线动成面：一条线段平移，扫过形成一个平面（3）面动成体：直角三角形绕着直角边旋转，形成一个圆锥体2、旋转成的立体图形一般地，某些含有曲面的几何体可以由某一个平面旋转得到例：如图：CD是直角三角形ABC的高，将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是（）A．绕着AC旋转B．绕着AB旋转C．绕着CD旋转D．绕着BC旋转。

人教版数学七年级上册第一章
人教版数学七年级上册第一章是《有理数》。

本章主要介绍了有理数的概念、性质和运算。

具体内容包括：
1. 有理数的定义：有理数是可以表示为两个整数的比的数，即形如a/b 的数，其中a、b是整数，且b≠0。

2. 有理数的性质：有理数具有相反数、绝对值、加法和减法等基本性质。

3. 有理数的加减法：介绍了有理数的加法和减法运算法则，包括同号相加、异号相减、绝对值相减等。

4. 有理数的乘法：介绍了有理数的乘法运算法则，包括同号相乘、异号相乘等。

5. 有理数的除法：介绍了有理数的除法运算法则，包括同号相除、异号相除等。

6. 有理数的应用：通过实际问题，介绍了有理数在实际生活中的应用，如计算物品的价格、长度等。

人教版数学七年级上册第一章有理数1.1正数和负数①我们知道，像3,1.8％，3.5这样大于0的数叫做正数。

像-3，-2.7％，-4.5，-1.2这样在正数前加上符号“-”（负）的数叫做负数。

有时，为了明确表达意义，在正数前面也加上“+”（正）号。

例如，+3，+2，+0.5，+13，…就是3，2, 0.5，13…。

一个数前面的“+”“-”号叫做它的符号。

②0既不是正数，也不是负数。

③中国古代用算筹（表示数的工具）进行计算，红色算筹表示正数，黑色算筹表示负数。

④把0以外的数分为正数和负数，它们表示具有相反意义的量。

随着对正数、负数意义认识的加深，正数和负数在实践中得到了广泛应用。

在地形图上表示某地的高度时，需要以海平面为基准（规定海平面的海拔高度为0m），通常用正数表示高于海平面的某地某地的海拔高度，用负数表示低于海平面的某地的海拔高度。

例如，珠穆朗玛峰的海拔高度为8844.43m。

吐鲁番盆地的海拔高度为-155m。

记账时，通常用正数表示收入款额，用负数表示支出款额。

⑤0是正数与分数的分界。

0℃是一个确定的温度，海拔0m表示海平面的平均高度。

0的意义已不仅是表示“没有”。

1.2.1有理数①我们学过的数有：正整数，如1，2,3，…；零，0；负整数，如-1，-2，-3，…；正分数，如12，23，157，0.1,5.32，…；负分数，如-0.5，-52，-23，-17，-150.25，…。

②正整数、0、负整数统称为整数；正分数、负分数统称为分数。

③整数和分数统称为有理数（rational numbe）。

④从小学开始，我们首先认识了正整数，后来又增加了0和正分数，在认识了负整数和负分数后，对数的认识就扩充到了有理数范围。

1.2.2数轴①在数学中，可以用一条直线上的点表示数，这条直线叫做数轴（number axis），它满足以下要求：⑴在直线上任取一个点表示数0，这个点叫做原点（origin）；⑵通常规定直线上从原点向右（或上）为正方向，从原点向左（或下）为负方向；⑶0是正数和负数的分界点；原点是数轴的“基准点”。

七年级上册地理第一章地球与地图知识点梳理一、地球的形状、大小1、提出证据说明地球是个球体：（1）站在海边，遥望远处驶来的船只，总是先看到桅杆，再看见船身，而且送离岸的船总是船身先消失，桅杆后消失。

（2）站得高，看得远(登高望远)。

（3）发生月偏食时，地球挡住一部分月光，使地球的影子投射在月面上，就像给地球照镜子，使我们看见了地球的球体形状。

（4）北极星的高度因纬度而异；（5）麦哲伦环球航行；（6）卫星照片2、用平均半径、赤道周长和表面积描述地球的大小。

平均半径：6371千米；赤道周长：约4万千米；地球表面积：5.1亿平方千米。

3、运用地球仪，说出经线与纬线，经度与纬度的划分。

(1)比较经线和纬线的特点：4、经纬网：准确描述一个地点的地理位置，例如北京：40°N，116°E注意：除南北极点外，任何其他地点位置的描述都由一经一纬组成，且要注明东西经南北纬（0°纬线、0°经线、180°经线不需要方向）二、用事实分别说明地球自转、公转及其产生的地理现象1、太阳光线的直射点有规律地在南北回归线之间来回移动。

夏至日（6月22日前后）太阳直射点在北回归线；冬至日（12月22日前后）太阳直射点在南回归线；春分日（3月21日前后）和秋分日（9月23日前后）太阳直射点在赤道上。

北半球与南半球的季节相反（春——秋；夏——冬）2、地球表面五带的划分：北寒带（66.5°N --90°N）、北温带（23.5°N --66.5°N）、热带（23.5°N --23.5°S）、南温带（23.5°S --66.5°S）、南寒带（66.5°S--90°S）3、寒带：有极昼极夜现象，气候终年寒冷；热带：有阳光直射现象，气候终年炎热；温带：既无阳光直射现象，又无极昼极夜现象，四季变化明显重点图：P11图1.19，P12图1.20 三、地图1、地图三要素：比例尺、方向和图例 （1）比例尺：①比例尺的计算：实地距离图上距离比例尺比例尺是个分式，分母越大，比例尺越小；分母越小，比例尺越大。

七年级数学上册知识点总结第一章第一章有理数一.正数和负数⒈正数和负数的概念负数：比0小的数正数：比0大的数 0既不是正数，也不是负数留意：①字母a可以表示任意数，当a表示正数时，-a是负数;当a表示负数时，-a是正数;当a表示0时，-a仍是0。

(假如出推断题为：带正号的数是正数，带负号的数是负数，这种说法是错误的，例如+a,-a就不能做出简洁推断)②正数有时也可以在前面加“+”，有时“+”省略不写。

所以省略“+”的正数的符号是正号。

2.具有相反意义的量若正数表示某种意义的量，则负数可以表示具有与该正数相反意义的量，比如：零上8℃表示为：+8℃;零下8℃表示为：-8℃支出与收入;增加与削减;盈利与亏损;北与南;东与西;涨与跌;增长与降低等等是相对相反量，它们计数：比原先多了的数,增加增长了的数一般记为正数;相反，比原先少了的数，削减降低了的数一般记为负数。

3.0表示的意义⑴0表示“没有”，如教室里有0个人，就是说教室里没有人;⑵0是正数和负数的分界线，0既不是正数，也不是负数。

二.有理数1.有理数的概念⑴正整数、0、负整数统称为整数(0和正整数统称为自然数)⑵正分数和负分数统称为分数⑶正整数，0，负整数，正分数，负分数都可以写成分数的形式，这样的数称为有理数。

理解：只有能化成分数的数才是有理数。

①π是无限不循环小数，不能写成分数形式，不是有理数。

②有限小数和无限循环小数都可化成分数，都是有理数。

留意：引入负数以后，奇数和偶数的范围也扩大了，像-2,-4,-6,-8…也是偶数，-1,-3,-5…也是奇数。

2. (1)凡能写成形式的数，都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.留意：0即不是正数，也不是负数;-a不肯定是负数，+a也不肯定是正数;p不是有理数;(2)有理数的分类: ①按正、负分类:②按有理数的意义来分:总结：①正整数、0统称为非负整数(也叫自然数)②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数(3)留意：有理数中，1、0、-1是三个特别的数，它们有自己的特性;这三个数把数轴上的数分成四个区域，这四个区域的数也有自己的特性;(4)自然数? 0和正整数;a0 ? a是正数;a0 ? a是负数;a≥0 ? a是正数或0 ? a是非负数;a≤ 0 ? a是负数或0 ? a 是非正数.三.数轴⒈数轴的概念规定了原点，正方向，单位长度的直线叫做数轴。