昆明理工大学材料力知识学习题册14概念标准答案
- 格式:doc
- 大小:882.25 KB
- 文档页数:29

第一章 静力学基础二、填空题–F sin α; F cos α; F cos α; F sin α ; 0 ;F ; F sin α; F cos α。
1200, 0 。
外 内 。
约束 ; 相反 ; 主动 主动 。
3 ,力偶矩代数值相等(力偶矩的大小相等,转向相同) 。
三、选择题(c) 。
3.2 A 。
D 。
D 。
3.5 A 。
B 。
3.7 C 。
四、计算题(emmKN F M ⋅-=18030)(mmKN F M ⋅=-=3.2815325)(20mmKN F M ⋅-=25210.)(01=)(F M x m N F M y ⋅-=501)(01=)(F M z mN F M x ⋅-=2252)(mN F M y ⋅-=2252)(mN F M z ⋅=2252)(mN F M z ⋅=2253)(五 、受力图(a(b(cB B(a(b(cP 2(dmN F M x ⋅=2253)(mN F M y ⋅-=2253)((1) 小球(2) 大球PPACB (a(1) AC 杆(2) CB 杆(1) AC 段梁 (2) CD 段梁(1) AB 杆(2) CD 杆P第二章 力系的简化一、是非判断题 ( × ) ( ∨ )( × )二、填空题 平衡 。
(1) CD 杆 (2) AB 杆(i(1) 滑轮D (2) AB 杆(jDDF PPAB KIBCF AY AX IY IX KY CID,DF ,BCF 'IX 'I Y DCE,EFFCF ABE.EF AY AX BY BX CA O,C F ,A Y ,AXY 0X ACP FBCPA Y AX B Y BX CY CX CX 'CY 'CX 'CY 'DY分布载荷图形的面积 , 合力矩定理 , 分布载荷图形的形心 。
平行力系合力的作用点 ; 物体合重力的作用点 ; 物体的几何中心 。

完整版材料⼒学性能课后习题答案整理材料⼒学性能课后习题答案第⼀章单向静拉伸⼒学性能1、解释下列名词。
1弹性⽐功:⾦属材料吸收弹性变形功的能⼒,⼀般⽤⾦属开始塑性变形前单位体积吸收的最⼤弹性变形功表⽰。
2、滞弹性:⾦属材料在弹性范围内快速加载或卸载后,随时间延长产⽣附加弹性应变的现象称为滞弹性,也就就是应变落后于应⼒的现象。
3、循环韧性:⾦属材料在交变载荷下吸收不可逆变形功的能⼒称为循环韧性。
4、包申格效应:⾦属材料经过预先加载产⽣少量塑性变形,卸载后再同向加载,规定残余伸长应⼒增加;反向加载,规定残余伸长应⼒降低的现象。
5、解理刻⾯:这种⼤致以晶粒⼤⼩为单位的解理⾯称为解理刻⾯。
6.塑性:⾦属材料断裂前发⽣不可逆永久(塑性)变形的能⼒。
脆性:指⾦属材料受⼒时没有发⽣塑性变形⽽直接断裂的能⼒韧性:指⾦属材料断裂前吸收塑性变形功与断裂功的能⼒。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成⼀个⾼度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动⽽相互汇合,同号台阶相互汇合长⼤,当汇合台阶⾼度⾜够⼤时,便成为河流花样。
就是解理台阶的⼀种标志。
9.解理⾯:就是⾦属材料在⼀定条件下,当外加正应⼒达到⼀定数值后,以极快速率沿⼀定晶体学平⾯产⽣的穿晶断裂,因与⼤理⽯断裂类似,故称此种晶体学平⾯为解理⾯。
10、穿晶断裂:穿晶断裂的裂纹穿过晶内,可以就是韧性断裂,也可以就是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数就是脆性断裂。
11、韧脆转变:具有⼀定韧性的⾦属材料当低于某⼀温度点时,冲击吸收功明显下降,断裂⽅式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、说明下列⼒学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应⼒ 2.0σ屈服强度 gt δ⾦属材料拉伸时最⼤应⼒下的总伸长率 n 应变硬化指数P15 3、⾦属的弹性模量主要取决于什么因素?为什么说它就是⼀个对组织不敏感的⼒学性能指标?答:主要决定于原⼦本性与晶格类型。

S 1S 2 第十四章 光学一、选择题1. 有三种装置(1)完全相同的两盏钠光灯,发出相同波长的光,照射到屏上;(2)同一盏钠光灯,用黑纸盖住其中部,将钠光灯分成上下两部分,同时照射到屏上;(3)用一盏钠光灯照亮一狭缝,此亮缝再照亮与它平行,且间距很小的两条狭缝,此二亮缝的光照射到屏上。
以上三种装置,能在屏上形成稳定干涉花样的是:[ A ](A )装置(3) (B )装置(2) (C )装置(1)、(3) (D )装置(2)(3)2. 在真空中波长为λ的单色光,在折射率为n 的透明介质中从A 沿某路径传播到B ,若A 、B 两点相位差为3π,则此路径AB 的光程为:[ A ](A )1.5λ (B )1.5λ/n (C )1.5n λ (D )3λ3. 在相同的时间内,一束波长为λ的单色光在空气中和在玻璃中:[ C ](A )传播的路程相等,走过的光程相等; (B )传播的路程相等,走过的光程不相等;(C )传播的路程不相等,走过的光程相等; (D )传播的路程不相等,走过的光程不相等。
4. 如图,如果S 1、S 2是两个相干光源,它们到P 点的距离分别为r 1和r 2,路径S 1P 垂直穿过一块厚度为t 1,折射率为n 1的介质板,路径S 2P 垂直穿过厚度为t 2,折射率为n 2的另一介质板,其余部分为真空,光沿这两条路径的光程差等于:[ B ](A ) 222111()();r n t r n t +-+(B ) 222111[(1)][(1)];r n t r n t +--+- (C ) 222111()();r n t r n t ---(D ) 2211n t n t -5. 双缝干涉实验中,入射光波长为λ,用玻璃纸遮住其中一缝,若玻璃纸中光程比相同厚度的空气大λ5.2,则屏上原0级明纹中心处 [ B ](A ) 仍为明纹中心 (B ) 变为暗纹中心(C ) 不是最明,也不是最暗 (D ) 无法确定6. 如图所示,用波长600=λnm 的单色光做杨氏双缝实验,在光屏P 处产生第五级明纹极大,现将折射率n =1.5的薄透明玻璃片盖在其中一条缝上,此时P 处变成中央明纹极大的位置,则此玻璃片厚度为:[ B ](A ) 5.0×10-4cm (B ) 6.0×10-4cm(C ) 7.0×10-4cm (D ) 8.0×10-4cm7. 在照相机镜头的玻璃片上均匀镀有一层折射率n 小于玻璃的介质薄膜,以增强某一波长λ 的透射光能量。

材料科学基础习题与参考答案(doc14页)完美版第⼀章材料的结构⼀、解释以下基本概念空间点阵、晶格、晶胞、配位数、致密度、共价键、离⼦键、⾦属键、组元、合⾦、相、固溶体、中间相、间隙固溶体、置换固溶体、固溶强化、第⼆相强化。
⼆、填空题1、材料的键合⽅式有四类,分别是(),(),(),()。
2、⾦属原⼦的特点是最外层电⼦数(),且与原⼦核引⼒(),因此这些电⼦极容易脱离原⼦核的束缚⽽变成()。
3、我们把原⼦在物质内部呈()排列的固体物质称为晶体,晶体物质具有以下三个特点,分别是(),(),()。
4、三种常见的⾦属晶格分别为(),()和()。
5、体⼼⽴⽅晶格中,晶胞原⼦数为(),原⼦半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶⾯为(),晶胞中⼋⾯体间隙个数为(),四⾯体间隙个数为(),具有体⼼⽴⽅晶格的常见⾦属有()。
6、⾯⼼⽴⽅晶格中,晶胞原⼦数为(),原⼦半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶⾯为(),晶胞中⼋⾯体间隙个数为(),四⾯体间隙个数为(),具有⾯⼼⽴⽅晶格的常见⾦属有()。
7、密排六⽅晶格中,晶胞原⼦数为(),原⼦半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶⾯为(),具有密排六⽅晶格的常见⾦属有()。
8、合⾦的相结构分为两⼤类,分别是()和()。
9、固溶体按照溶质原⼦在晶格中所占的位置分为()和(),按照固溶度分为()和(),按照溶质原⼦与溶剂原⼦相对分布分为()和()。
10、影响固溶体结构形式和溶解度的因素主要有()、()、()、()。
11、⾦属化合物(中间相)分为以下四类,分别是(),(),(),()。
12、⾦属化合物(中间相)的性能特点是:熔点()、硬度()、脆性(),因此在合⾦中不作为()相,⽽是少量存在起到第⼆相()作⽤。
13、CuZn、Cu5Zn8、Cu3Sn的电⼦浓度分别为(),(),()。

第一章 绪论一、是非判断题1.1 ( × );1.2 ( × );1.3 ( × );1.4 ( ∨ );1.5 ( ∨ );1.6 ( ∨ ) 1.7 ( ∨ );1.8 ( × );1.9 ( × );1.10 ( ∨ );1.11 ( ∨ )1.12 ( ∨ );1.13 ( × );1.14 ( ∨ );1.15 ( ∨ ) ;1.16 ( × )二、填空题1.1 杆件 变形 , 应力,应变 。
1.2 外力的合力作用线通过杆轴线 , 沿杆轴线伸长或缩短 。
1.3 受一对等值,反向,作沿剪切面发生相对错动 , 沿剪切面发生相对错动 。
1.4 外力偶作用面垂直杆轴线 。
任意二横截面发生绕杆轴线的相对转动 。
1.5 外力作用线垂直杆轴线,外力偶作用面通过杆轴线 , 梁轴线由直线变为曲线 。
1.6 包含两种或两种以上基本变形的组合 。
1.7 强度 , 刚度 , 稳定性 。
1.8 强度 , 刚度 , 稳定性 。
1.9 连续性 , 均匀性 , 各向同性 。
1.10 连续性假设 。
应力 、 应变 变形等 。
1.11 拉伸 , 压缩 , 弯曲 。
1.12 2α ; α-β ; 0 。
三、选择题1.1 1 。
1.2 C 。
1.3 C 。
四、计算题1.10=A X ∑=0X FF S =⇒∑=0Y 0=-F Y A F Y A =⇒∑=0A M 0=--FL M FL M -=⇒y x解:1. 求A 端的反力: 2. 求1-1截面的内力: ∑=0Y 0=F F S-∑=01C M 02=--/FL M 2/FL M -=⇒X A M1.2第二章 拉伸、压缩与剪切一、是非判断题2.1 ( × );2.2 ( ×);2.3 ( × );2.4. ( ×);2.5 ( × );2.6 ( × ) 2.7 ( × );2.9 ( × );2.10 ( × );2.11( × );2.12( ∨ )二、填空题2.1 2.22.3 最大工作应力σmax 不超过许用应力[σ] , 强度校核 ; 截面设计 ; 确定许可载荷 。


完整版材料⼒学性能课后习题答案整理材料⼒学性能课后习题答案第⼀章单向静拉伸⼒学性能1、解释下列名词。
1弹性⽐功:⾦属材料吸收弹性变形功的能⼒,⼀般⽤⾦属开始塑性变形前单位体积吸收的最⼤弹性变形功表⽰。
2.滞弹性:⾦属材料在弹性范围内快速加载或卸载后,随时间延长产⽣附加弹性应变的现象称为滞弹性,也就是应变落后于应⼒的现象。
3.循环韧性:⾦属材料在交变载荷下吸收不可逆变形功的能⼒称为循环韧性。
4.包申格效应:⾦属材料经过预先加载产⽣少量塑性变形,卸载后再同向加载,规定残余伸长应⼒增加;反向加载,规定残余伸长应⼒降低的现象。
5.解理刻⾯:这种⼤致以晶粒⼤⼩为单位的解理⾯称为解理刻⾯。
6.塑性:⾦属材料断裂前发⽣不可逆永久(塑性)变形的能⼒。
脆性:指⾦属材料受⼒时没有发⽣塑性变形⽽直接断裂的能⼒韧性:指⾦属材料断裂前吸收塑性变形功和断裂功的能⼒。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成⼀个⾼度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动⽽相互汇合,同号台阶相互汇合长⼤,当汇合台阶⾼度⾜够⼤时,便成为河流花样。
是解理台阶的⼀种标志。
9.解理⾯:是⾦属材料在⼀定条件下,当外加正应⼒达到⼀定数值后,以极快速率沿⼀定晶体学平⾯产⽣的穿晶断裂,因与⼤理⽯断裂类似,故称此种晶体学平⾯为解理⾯。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有⼀定韧性的⾦属材料当低于某⼀温度点时,冲击吸收功明显下降,断裂⽅式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、说明下列⼒学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应⼒ 2.0σ屈服强度 gt δ⾦属材料拉伸时最⼤应⼒下的总伸长率 n 应变硬化指数P153、⾦属的弹性模量主要取决于什么因素?为什么说它是⼀个对组织不敏感的⼒学性能指标?答:主要决定于原⼦本性和晶格类型。
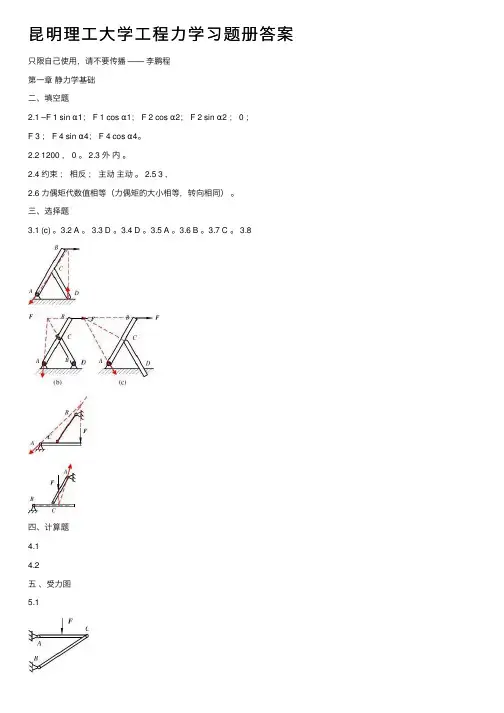
昆明理⼯⼤学⼯程⼒学习题册答案只限⾃⼰使⽤,请不要传播 —— 李鹏程第⼀章静⼒学基础⼆、填空题2.1 –F 1 sin α1; F 1 cos α1; F 2 cos α2; F 2 sin α2 ; 0 ;F 3 ; F 4 sin α4; F 4 cos α4。
2.2 1200 , 0 。
2.3 外内。
2.4 约束;相反;主动主动。
2.5 3 ,2.6 ⼒偶矩代数值相等(⼒偶矩的⼤⼩相等,转向相同)。
三、选择题3.1 (c) 。
3.2 A 。
3.3 D 。
3.4 D 。
3.5 A 。
3.6 B 。
3.7 C 。
3.8四、计算题4.14.2五、受⼒图5.1B(e)(d) (a) mm KN F M ?-=18030)(mm KN F M ?=-=3.2815325)(20mm KN F M ?-=25210.)(01=)(F M x m N F M y ?-=501)(01=)(F M z m N F M x ?-=2252)(m N F M y ?-=2252)(m N F M z ?=2252)(mN F M x ?=2253)(mN F M y ?-=2253)(mN F M z ?=2253)(5.25.3(b)(c)P 2(d)(1) ⼩球 (2) ⼤球(3) 两个球合在⼀起ACB(1) AB 杆 (2) CD 杆 (3)整体只限⾃⼰使⽤,请不要传播 —— 李鹏程(1) AC 杆(2) CB 杆 (3)整体(1) AC 段梁 (2) CD 段梁(3)整体(1) CD 杆 (2) AB 杆 (3) OA 杆C(1) 滑轮D (2) AB 杆 (3) CD 杆只限⾃⼰使⽤,请不要传播——李鹏程第⼆章⼒系的简化⼀、是⾮判断题1.1( ×) 1.2( ∨) 1.2( ×)⼆、填空题2.1 平衡。
2.2 分布载荷图形的⾯积,合⼒矩定理,分布载荷图形的形⼼。
2.3平⾏⼒系合⼒的作⽤点;物体合重⼒的作⽤点;物体的⼏何中⼼。

完整版材料力学性能课后习题答案整理材料力学性能课后习题答案第一章单向静拉伸力学性能1、解释下列名词。
1弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5.解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
脆性:指金属材料受力时没有发生塑性变形而直接断裂的能力韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成一个高度为b的台阶。
8.河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的一种标志。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变2、 说明下列力学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 P153、 金属的弹性模量主要取决于什么因素?为什么说它是一个对组织不敏感的力学性能指标?答:主要决定于原子本性和晶格类型。

昆明理工大学2006~2007学年第二学期《材料力学》期末考试试卷(A 卷)一、是非判断题(每题2分,共20分。
正确用√,错误用×,填入括号中)1 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( )2甲、乙两杆几何尺寸相同,轴向拉力相同,材料不同,则它们的应力和变形均相同。
( )3 单元体上同时存在正应力和切应力时,切应力互等定理不成立。
( )4 正弯矩产生正转角,负弯矩产生负转角。
( )5 单元体最大正应力面上的切应力恒等于零。
( )6 在近乎等值的三向拉应力作用下,钢等塑性材料只可能发生断裂。
( )7 空心圆轴的外径为D 、内径为d ,其极惯性矩和扭转截面系数分别为1616,32323344d D W d D I t p ππππ-=-=( ) 8 应变为无量纲量。
( ) 9 构件在交变应力下的疲劳破坏与静应力下的失效本质是相同的。
( )10 若一对正交坐标轴中,其中有一轴为图形的对称轴,则图形对这对轴的惯性积一定为零。
( )二、选择题(每题3分,共12分)1、 满足平衡条件,但切应力超过比例极限时,下列说法正确的是 。
A B C D切应力互等定理: 成立 不成立 不成立 成立 剪切虎克定律: 成立 不成立 成立 不成立2、长度和横截面面积均相同的两杆,一为钢杆,另一为铝杆,在相同的轴向拉力作用下,两杆的应力与变形有四种情况;正确答案是(A )铝杆的应力和钢杆相同,变形大于钢杆; (B) 铝杆的应力和钢杆相同,变形小于钢杆; (C )铝杆的应力和变形均大于钢杆; (D) 铝杆的应力和变形均小于钢杆。
3、由低碳钢、木材和灰铸铁三种材料制成的扭转圆轴试件,受扭后破坏现象呈现为:图(b ),扭角不大即沿45º螺旋面断裂;图(c ),发生非常大的扭角后沿横截面断开;图(d ),表面出现纵向裂纹。
据此判断试件的材料为,低碳钢为图 ;木材为图 ,灰铸铁为图 。
4、图示各单元体中 为单向应力状态, 为纯剪应力状态。
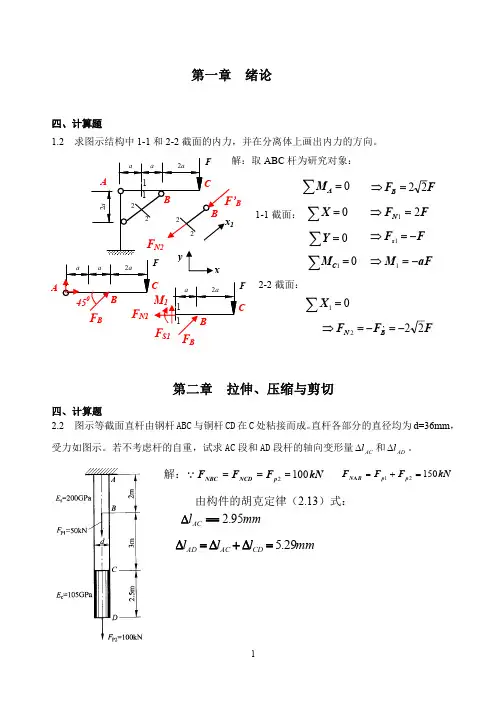
工程力学习题集只限自己使用,请不要传播昆明理工大学李鹏程第一章静力学基础二、填空题2.1 -F i sin a ; F i cos a ; F 2 cos 02 ; F 2 sin a ; ___ 0 ___ ; _F 3_ ; F 4 sin 0; F 4 cos a 4。
2.2 _____ 120° _____ , __________ 0 __________ 。
2.3 —外 __________________ 内 ___________ 。
2.4 —约束 —; __________ 相反 _______ ; ________ 主动 _______________ 主动2.5 ___ 3—,2.6___ 偶矩代数值相等(力偶矩的大小相等,转向相同) —。
三、选择题3.1 _(c)_。
3.2 _A_。
3.3 D 。
3.4 _D_。
3.5 _A_。
3.6 _B_。
3.7 _C ____________________3.8M 0(F 3) = -180KN mm4.2M x (FJ = 0M x (F 2尸-25 2N m M x (F )= 25.2N m(a) 四、计算题 (b) (c)(d)4.1M 0(F 1) - -2.5 2 KN mmM °(F 2) =25-3-15 =28.3 KN mm五、受力图 M y (FJ - -50N m M y (F 2) = -25. 2N m M y (F 3) = -25 2N mM z (F 1) = 0 M z (F 2) =25 2N m Mzkp25 2N m5.2 (c)P 25.3 (1) 小球(2) 大球(3) 两个球合在一起PAEC口(1) AB 杆 ⑵CD 杆 ⑶整体只限自己使用,请不要传播李鹏程T AP IBCP2T A T BCB(c)(1) AC 杆(2) CB 杆Y B (3)整体S HII X A^.B YB (d)(1) AC段梁(2) CD段梁⑶整体vY D(1) CD 杆⑵AB杆⑶0A杆Y D(1) 滑轮D(2) AB 杆⑶CD杆只限自己使用,请不要传播李鹏程Y AX 。
只限自己使用,请不要传播 —— 李鹏程第一章 静力学基础一、是非判断题 1.1 ( ∨ ) 1.2 ( × ) 1.3 ( × ) 1.4 ( ∨ ) 1.5 ( × ) 1.6 ( × ) 1.7 ( × ) 1.8 ( ∨ ) 1.9 ( × ) 1.10 ( × ) 1.11 ( × ) 1.12 ( × ) 1.13 ( ∨ ) 1.14 ( × ) 1.15 ( ∨ )1.162.1 2.2 2.3 外 内 。
2.4 约束 ; 相反 ; 主动 主动 。
2.5 3 ,2.6 力偶矩代数值相等(力偶矩的大小相等,转向相同) 。
三、选择题3.1 (c) 。
3.2 A 。
3.3 D 。
3.4 D 。
3.5 A 。
3.6 B 。
3.7 C 。
3.8四、计算题4.14.2(e)(d) (a)mm KN F M ⋅-=18030)(mm KN F M ⋅=-=3.2815325)(20mm KN F M ⋅-=25210.)(01=)(F M x m N F M y ⋅-=501)(01=)(F M z m N F M x ⋅-=2252)(m N F M y ⋅-=2252)(mN F M z ⋅=2252)(mN F M x ⋅=2253)(mN F M y ⋅-=2253)(mN F M z ⋅=2253)(只限自己使用,请不要传播 —— 李鹏程五 、受力图 5.15.2(a)(b) B B(b) (c) P 2(d)只限自己使用,请不要传播 —— 李鹏程5.3(1) 小球 (2) 大球 (3) 两个球合在一起 P 2P 1A CB (a)(1) AC 杆 (2) CB 杆 (3)整体(1) AC 段梁 (2) CD 段梁 (3)整体 (1) AB 杆 (2) CD 杆(3)整体只限自己使用,请不要传播——李鹏程第二章力系的简化一、是非判断题1.1( ×) 1.2( ∨) 1.2( ×)二、填空题2.1 平衡。
第一章 静力学基础二、填空题2.1 –F 1 sin α1; F 1 cos α1; F 2 cos α2; F 2 sin α2 ; 0 ;F 3 ; F 4 sin α4; F 4 cos α4。
2.2 1200, 0 。
2.3 外 内 。
2.4 约束 ; 相反 ; 主动 主动 。
2.5 3 ,2.6 力偶矩代数值相等(力偶矩的大小相等,转向相同) 。
三、选择题 3.1 (c) 。
3.2 A 。
3.3 D 。
3.4 D 。
3.5 A 。
3.6 B 。
3.7 C 。
3.8四、计算题4.1(d)(a) (b) (c)mmKN F M ⋅-=18030)(mmKN F M ⋅=-=3.2815325)(20mmKN F M ⋅-=25210.)(4.2五 、受力图5.15.2(a)(c)ACCAB B(b)1=)(F M x mN F M y ⋅-=501)(01=)(F M z m N F M x ⋅-=2252)(m N F M y ⋅-=2252)(mN F M z ⋅=2252)(mN F M x ⋅=2253)(mN F M y ⋅-=2253)(mN F M z ⋅=2253)(qAM BA(c)P 2(d)5.3(1) 小球 (2) 大球(3) 两个球合在一起P 2P 1ACB(a)(1) AB 杆 (2) CD 杆 (3)整体(1) AC杆(2) CB杆(3)整体(1) AC段梁(2) CD段梁(3)整体第二章 力系的简化一、是非判断题1.1 ( × ) 1.2 ( ∨ ) 1.2 ( × ) 二、填空题2.1 平衡 。
2.2 分布载荷图形的面积 , 合力矩定理 , 分布载荷图形的形心 。
2.3 平行力系合力的作用点 ; 物体合重力的作用点 ; 物体的几何中心 。
三、计算题 3.1F 3F 1ykNX 98340.=⋅⋅⋅=∑kNY 13587.=⋅⋅⋅=∑解:由(2.10)式:kNY X F R 9667822.)()('=+=∑∑(1) CD 杆 (2) AB 杆 (3) OA 杆C(i)(1) 滑轮D (2) AB 杆 (3) CD 杆(j)DDF PPABKIBCF AY AX IY IX KY CID,DF ,BCF 'IX 'I Y DCE,EFFCF ABE.EF AY AX BY BX CAO,CF,A Y ,AXY 0X3.2第三章 力系的平衡方程及其应用一、是非判断题1.1 ( ∨ ) ;1.2 ( × );1.3 ( ∨ ) ;1.4 ( × );1.5 ( × );1.6 ( ∨ )(a)(b)5020.cos '==∑R F Xα8650.cos '==∑R F Y βcmkN FM M i ⋅=⋅⋅⋅==∑58460000.)(kNF F R R 96678.'==cm F M d R7860.'==M=c mmc 086.=mm125.mm1210.由(2.14)式:二、填空题2.1 力偶矩的代数值相等 ; 。
练习1 绪论及基本概念1-1 是非题(1)材料力学是研究构件承载能力的一门学科。
( 是 )(2)可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
(是 )(3)构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。
( 是 ) (4)应力是内力分布集度。
(是 )(5)材料力学主要研究构件弹性范围内的小变形问题。
(是 ) (6)若物体产生位移,则必定同时产生变形。
(非 ) (7)各向同性假设认为,材料沿各个方向具有相同的变形。
(F )(8)均匀性假设认为,材料内部各点的力学性质是相同的。
(是)(9)根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。
(非) (10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(非 )1-2 填空题(1)根据材料的主要性质对材料作如下三个基本假设:连续性假设 、均匀性假设 、 各向同性假设 。
(2)工程中的 强度 ,是指构件抵抗破坏的能力; 刚度 ,是指构件抵抗变形的能力。
(3)保证构件正常或安全工作的基本要求包括 强度 , 刚度 ,和 稳定性 三个方面。
(4)图示构件中,杆1发生 拉伸 变形,杆2发生 压缩 变形, 杆3发生 弯曲 变形。
(5)认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为 连续性假设 。
根据这一假设构件的应力,应变和位移就可以用坐标的 连续 函数来表示。
(6)图示结构中,杆1发生 弯曲 变形,构件2发生 剪切 变形,杆件3发生 弯曲与轴向压缩组合。
变形。
(7)解除外力后,能完全消失的变形称为 弹性变形 ,不能消失而残余的的那部分变形称为 塑性变形 。
(8)根据 小变形 条件,可以认为构件的变形远 小于 其原始尺寸。
1-3 选择题(1)材料力学中对构件的受力和变形等问题可用连续函数来描述;通过试件所测得的材料的力学性能,可用于构件内部的任何部位。
昆明理工大学工程力学习题册答案一、选择题1. 在平面力系中,力对点的矩的常用单位是(A)A. N·mB. N/mC. N·sD. N·m^2答案:A2. 平面汇交力系的平衡方程是(C)A. Fx=0, Fy=0, M=0B. Fx=0, Fy=0C. Fx=0, Fy=0, M=0(其中M为力矩)D. Fx=0, Fy=0, M≠0答案:C3. 在空间力系中,力的投影与原力的关系是(B)A. 投影等于原力B. 投影小于等于原力C. 投影大于原力D. 投影与原力无关答案:B二、填空题1. 力对物体的作用效果包括______和______。
答案:使物体发生形变,使物体产生运动2. 平面力系中的合力可以用______和______来确定。
答案:力的大小,力的方向3. 在平面力系中,力矩的计算公式为______。
答案:M=F×d(其中F为力,d为力臂)三、计算题1. 已知:力F=10N,作用点距离A点4cm,求力F 对A点的力矩。
解:力矩的计算公式为M=F×d,其中d为力臂,即作用点到力作用点的距离。
本题中,d=4cm=0.04m。
所以,M=10N×0.04m=0.4N·m。
答案:0.4N·m2. 平面汇交力系中,已知F1=20N,F2=30N,F3=40N,求该力系的合力。
解:首先,将F1和F2合成,得到合力F12。
F12的大小为F12=√(F1^2+F2^2+2F1F2cosθ),其中θ为F1和F2之间的夹角。
假设F1和F2之间的夹角为60°,则F12=√(20^2+30^2+2×20×30×cos60°)=√(400+900+ 1200×0.5)=√(2000)=44.72N。
然后,将F12与F3合成,得到合力F123。
F123的大小为F123=√(F12^2+F3^2+2F12F3cosθ),其中θ为F12和F3之间的夹角。
昆明理工大学材料性能学1、低温脆性体心立方金属或合金:实验温度低于Tk时,韧性状态转变为脆性状态;断裂机理由微孔聚集变为穿晶解离;断口特征由纤维状变为结晶状。
面心立方金属无低温脆性。
3、冲击韧性表示单位面积吸收冲击功的平均值,由于缺口处应力分布不均,因此ak无明确的物理意义;ak可表示材料的脆性倾向,但不能真正反映材料的韧脆程度。
4、接触疲劳两接触材料作滚动或滚动加滑动摩擦时,交变接触压应力长期作用使材料表面疲劳损伤,局部区域出现小片或小块状材料剥落,而使材料磨损的现象。
5、蠕变材料在长时间的恒温、恒载荷作用下缓慢地产生塑性变形的现象。
6、断裂韧度KIC<KC,KIC是材料本身的力学性能指标,只与材料成分、组织结构有关。
10、滞弹性材料在加速加载或卸载后,随时间的延长而产生的附加弹性应变的性能。
组织越不均匀,温度越高,切应力分量越大,滞弹性就越明显。
11、磨损磨损是在摩擦作用下物体相对运动时,表面逐渐分离出磨屑,使接触表面不断发生尺寸变化与重量损失的现象。
12应力腐蚀由拉伸应力和腐蚀介质联合作用而引起的低应力脆性断裂称为应力腐蚀。
15、等强温度晶界和晶内强度相等的温度称为等温强度。
16、解理断裂在正应力作用力,由于原子间结合键破坏引起沿特定晶面发生脆性穿晶断裂称为解理断裂。
18、粘弹性 材料在外力作用下,弹性和粘性两种变形机理同时存在的力学行为。
其特征是应变对应力的响应不是瞬时完成的,需要通过一个弛豫过程。
19、内 耗 内耗是材料的一种重要的力学和物理性能,在力学上,内耗也称为材料的循环韧性,表示材料在交变载荷下吸收不可逆变形功的能力。
21、应力软性系数 α=Tmax/σmax ;α大表示切应力分量大,应力状态软,易塑性变形;α小表示正应力分量大,应力状态硬,易脆性断裂。
22、颈 缩 是一些金属材料和高分子材料在拉伸试验时,变形集中于局部区域的特殊状态,它是在应变硬化与截面减小的共同作用下,因应变硬化跟不上塑性变形的发展,使变形集中于试样局部区域而产生的。
^`第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( × ) 1.2 内力只作用在杆件截面的形心处。
( × ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( × ) 1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ∨ ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ∨ ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ∨ ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ∨ ) 1.8 同一截面上各点的正应力σ必定大小相等,方向相同。
( × ) 1.9 同一截面上各点的切应力τ必相互平行。
( × ) 1.10 应变分为正应变ε和切应变γ。
( ∨ ) 1.11 应变为无量纲量。
( ∨ ) 1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ∨ ) 1.13 若物体内各点的应变均为零,则物体无位移。
( × ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( ∨ ) 1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( ∨ )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( × )二、填空题1.1 材料力学主要研究 受力后发生的以及由此产生1.2 拉伸或压缩的受力特征是 ,变形特征是 。
B题1.15图题1.16图外力的合力作用线通过杆轴线 杆件^`1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
1.8 所谓 ,是指材料或构件抵抗破坏的能力。
所谓 ,是指构件抵抗变形的能力。
所谓 ,是指材料或构件保持其原有平衡形式的能力。
1.9 根据固体材料的性能作如下三个基本假设 , , 。
1.10 认为固体在其整个几何空间内无间隙地充满了组成该物体的物质,这样的假设称为 。
根据这一假设构件的 、 和 就可以用坐标的连续函数来表示。
1.11 填题1.11图所示结构中,杆1发生 变形,杆2发生 变形,杆3发生 变形。
1.12 下图 (a)、(b)、(c)分别为构件内某点处取出的单元体,变形后情况如虚线所示,则单元体(a)的切应变γ= ;单元体(b)的切应变γ= ;单元体(c)的切应变γ= 。
三、选择题1.1 选题1.1图所示直杆初始位置为ABC ,α>β αααααβ(a)(b)(c)填题1.11图’ 沿杆轴线伸长或缩短受一对等值,反向,作用线距离很近的力的作用 沿剪切面发生相对错动 外力偶作用面垂直杆轴线 任意二横截面发生绕杆轴线的相对转动 外力作用线垂直杆轴线,外力偶作用面通过杆轴线 梁轴线由直线变为曲线 包含两种或两种以上基本变形的组合 强度 刚度 稳定性 强度 刚度 稳定性 连续性 均匀性 各向同性 连续性假设应力应变 变形等 拉伸 压缩 弯曲 2α α-β 0作用力P 后移至AB’C’,但右半段BCDE的形状不发生变化。
试分析哪一种答案正确。
1、AB、BC两段都产生位移。
2、AB、BC 两段都产生变形。
正确答案是1。
选题1.1图1.2 选题1.2图所示等截面直杆在两端作用有力偶,数值为M,力偶作用面与杆的对称面一致。
关于杆中点处截面 A—A在杆变形后的位置(对于左端,由 A’—A’表示;对于右端,由 A”—A”表示),有四种答案,试判断哪一种答案是正确的。
正确答案是C。
选题1.2图1.3 等截面直杆其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是C。
选题1.3图第二章拉伸、压缩与剪切一、是非判断题2.1 因为轴力要按平衡条件求出,所以轴力的正负与坐标轴的指向一致。
( × ) 2.2 轴向拉压杆的任意截面上都只有均匀分布的正应力。
( × ) 2.3 强度条件是针对杆的危险截面而建立的。
( × ) 2.4. 位移是变形的量度。
( × )2.5 甲、乙两杆几何尺寸相同,轴向拉力相同,材料不同,则它们的应力和变形均相同。
( × )2.6 空心圆杆受轴向拉伸时,在弹性范围内,其外径与壁厚的变形关系是外径增大且壁厚也同时增大。
( × ) 2.7 已知低碳钢的σp =200MPa ,E =200GPa ,现测得试件上的应变ε=0.002,则其应力能用胡克定律计算为:σ=Eε=200×103×0.002=400MPa 。
( × )2.9 图示三种情况下的轴力图是不相同的。
( × )2.10 图示杆件受轴向力F N 的作用,C 、D 、E 为杆件AB 的三个等分点。
在杆件变形过程中,此三点的位移相等。
( × )2.11 对于塑性材料和脆性材料,在确定许用应力时,有相同的考虑。
( × ) 2.12连接件产生的挤压应力与轴向压杆产生的压应力是不相同的。
( ∨ ) 二、填空题2.1 轴力的正负规定为 。
2.2 受轴向拉伸或压缩的直杆,其最大正应力位于 横 截面,计算公式,最大切应力位于 450 截面,计算公式2.3 拉压杆强度条件中的不等号的物理意义是 最大工作应力σmax 不超过许用应力[σ] ,强度条件主要解决三个方面的问题是(1) 强度校核 ; (2) 截面设计 ;(3) 确定许可载荷 。
2.4 轴向拉压胡克定理的表示形式有 2 种,其应用条件是 σmax ≤σp 。
拉力为正,压力为负2.5 由于安全系数是一个__大于1_____数,因此许用应力总是比极限应力要___小___。
2.6 两拉杆中,A1=A2=A;E1=2E2;υ1=2υ2;若ε1′=ε2′(横向应变),则二杆轴力F N1_=__F N2。
2.7 低碳钢在拉伸过程中依次表现为弹性、屈服、强化、局部变形四个阶段,其特征点分别是σp,σe,σs,σb。
2.8 衡量材料的塑性性质的主要指标是延伸率δ、断面收缩率ψ。
2.9 延伸率δ=(L1-L)/L×100%中L1指的是拉断后试件的标距长度。
2.10 塑性材料与脆性材料的判别标准是塑性材料:δ≥5%,脆性材料:δ< 5%。
2.11 图示销钉连接中,2t2> t1,销钉的切应力τ=2F/πd2,销钉的最大挤压应力σbs=F/dt1。
2.12 螺栓受拉力F作用,尺寸如图。
若螺栓材料的拉伸许用应力为[σ],许用切应力为[τ],按拉伸与剪切等强度设计,螺栓杆直径d与螺栓头高度h的比值应取d/ h =4[τ]/[σ]。
2.13木榫接头尺寸如图示,受轴向拉力F作用。
接头的剪切面积A=hb,切应力τ=F/hb;挤压面积A bs=cb,挤压应力σbs=F/cb。
2.14 两矩形截面木杆通过钢连接器连接(如图示),在轴向力F作用下,木杆上下两侧的剪切面积A=2lb ,切应力τ=F/2lb;挤压面积A bs=2δb ,挤压应力σbs=F/2δb。
2.15挤压应力与压杆中的压应力有何不同挤压应力作用在构件的外表面,一般不是均匀分布;压杆中的压应力作用在杆的横截面上且均匀分布。
2.16图示两钢板钢号相同,通过铆钉连接,钉与板的钢号不同。
对铆接头的强度计算应包括: 铆钉的剪切、挤压计算;钢板的挤压和拉伸强度计算 。
若将钉的排列由(a )改为(b ),上述计算中发生改变的是 。
对于(a )、(b )两种排列,铆接头能承受较大拉力的是(a ) 。
(建议画板的轴力图分析)三、选择题2.1 为提高某种钢制拉(压)杆件的刚度,有以下四种措施:(A) 将杆件材料改为高强度合金钢; (B) 将杆件的表面进行强化处理(如淬火等); (C) 增大杆件的横截面面积; (D) 将杆件横截面改为合理的形状。
正确答案是 C 2.2 甲、乙两杆,几何尺寸相同,轴向拉力F 相同,材料不同,它们的应力和变形有四种可能:(A )应力σ和变形△l 都相同; (B) 应力σ不同,变形△l 相同; (C )应力σ相同,变形△l 不同; (D) 应力σ不同,变形△l 不同。
正确答案是 C 2.3 长度和横截面面积均相同的两杆,一为钢杆,另一为铝杆,在相同的轴向拉力作用下,两杆的应力与变形有四种情况;(A )铝杆的应力和钢杆相同,变形大于钢杆; (B) 铝杆的应力和钢杆相同,变形小于钢杆; (C )铝杆的应力和变形均大于钢杆; (D) 铝杆的应力和变形均小于钢杆。
正确答案是 A 2.4 在弹性范围内尺寸相同的低碳钢和铸铁拉伸试件,在同样载荷作用下,低碳钢试件的弹性变形为1δ,铸铁的弹性变形为2δ,则1δ与2δ的关系是;(A )1δ>2δ ; (B )1δ <2δ; (C )1δ =2δ ; (D )不能确定。
正确答案是 B钢板的拉伸强度计算 ∵ E ms > E ci见P33,表2.2∵ E s > E a2F 4F 43F FF)(+)(+2.5 等直杆在轴向拉伸或压缩时,横截面上正应力均匀分布是根据何种条件得出的。
(A )静力平衡条件; (B )连续条件;(C )小变形假设; (D 平面假设及材料均匀连续性假设。
正确答案是 D第三章 扭转一、是非判断题3.1 单元体上同时存在正应力和切应力时,切应力互等定理不成立。
( × ) 3.2 空心圆轴的外径为D 、内径为d ,其极惯性矩和扭转截面系数分别为1616,32323344d D W d D I t p ππππ-=-=( × )3.3 材料不同而截面和长度相同的二圆轴,在相同外力偶作用下,其扭矩图、切应力及相对扭转角都是相同的。
( × ) 3.4 连接件承受剪切时产生的切应力与杆承受轴向拉伸时在斜截面上产生的切应力是相同的。
( × ) 二、填空题3.1 图示微元体,已知右侧截面上存在与z 方向成θ 角的切应力τ,试根据切应力互等定理画出另外五个面上的切应力。
3.2 试绘出圆轴横截面和纵截面上的扭转切应力分布图。
填题3.2填题3.13.3 保持扭矩不变,长度不变,圆轴的直径增大一倍,则最大切应力τmax 是原来的 1/ 8 倍,单位长度扭转角是原来的 1/ 16 倍。
3.4 两根不同材料制成的圆轴直径和长度均相同,所受扭矩也相同,两者的最大切应力_________相等 __,单位长度扭转 _不同___ _______。